Genetic evidence for two founding populations of the Americas (original) (raw)
. Author manuscript; available in PMC: 2016 Aug 12.
Published in final edited form as: Nature. 2015 Jul 21;525(7567):104–108. doi: 10.1038/nature14895
Abstract
Genetic studies have been consistent with a single common origin of Native American groups from Central and South America1-4. However, some morphological studies have suggested a more complex picture, whereby the northeast Asian affinities of present-day Native Americans contrast with a distinctive morphology seen in some of the earliest American skeletons, which share traits with present-day Australasians (indigenous groups in Australia, Melanesia, and island southeast Asia)5-8. Here we analyze genome-wide data to show that some Amazonian Native Americans descend partly from a Native American founding population that carried ancestry more closely related to indigenous Australians, New Guineans and Andaman Islanders than to any present-day Eurasians or Native Americans. This signature is not present to the same extent or at all in present-day Northern and Central Americans or a ~12,600 year old Clovis genome, suggesting a more diverse set of founding populations of the Americas than previously accepted.
All Native American groups studied to date can trace all or much of their ancestry to a single ancestral population that likely migrated across the Bering land bridge from Asia more than 15,000 years ago2, with some Northern American and Arctic groups also tracing other parts of their ancestry to more recent waves of migration2,9,10. Ancient genomic evidence has shown that this so-called ‘First American’ ancestry is present in an individual associated with Clovis technology from North America dating to ~12,600 years ago3, and mitochondrial DNA has suggested that it was also present by 13,000-14,500 years ago11,12. In contrast, some morphological analyses of early skeletons in the Americas have suggested that characteristics of some Pleistocene and early Holocene skeletons fall outside the variation of present-day Native Americans, and instead within the variation of present-day indigenous Australians, Melanesians, and so-called ‘Negrito’ groups from Southeast Asia (and some sub-Saharan African groups)7,13. This morphology has been hypothesized to reflect an initial ‘Paleoamerican’ pioneer colonization of the Americas, which according to some interpretations was largely replaced by populations with Northeast Asian affinities in the early Holocene, but may have persisted in some locations14,15. However, morphological similarity can arise not only through shared descent but also through convergent evolution or phenotypic plasticity coupled with similar environments16,17. Another limitation of morphological data is that it provides very few independent characters that can be analyzed. Genome-wide data, with its hundreds of thousands of independent characters that evolve effectively neutrally, should be a statistically powerful and robust way to test whether a distinct lineage contributed to Native Americans.
Analysis of population history in the Americas is complicated by post-Columbian admixture from mainly European and African sources2. We identified 63 individuals without discernable evidence of European or African ancestry in 21 Native American populations genotyped at ~600,000 single nucleotide polymorphisms (SNPs) on the Affymetrix Human Origins array18,19 (SI 1; Extended Data Figure 1). We further restricted to individuals from Central and South America that have the strongest evidence of deriving entirely from a homogeneous First American ancestral population2. We computed all possible _f_4-statistics of the form _f_4(American1, American2; Outgroup1, Outgroup2), the product of the allele frequency differences between the two American groups and the two Outgroups. We represented the Americans by a panel of 7 Central and South American groups, and the Outgroups by 24 populations (4 from each of 6 worldwide regions). If the two Native American groups descend from a homogeneous ancestral population whose ancestors separated from the Outgroups at earlier times, it follows that the difference in allele frequencies between Native American populations will have developed entirely after their separation from the Outgroups, and so the correlation in allele frequency differences is expected to be zero. To evaluate whether all possible _f_4-statistics computed in this way are consistent with zero, correcting for multiple hypothesis testing due to the large number of statistics examined, we measured the empirical covariance of the matrix of _f4_-statistics using a Block Jackknife18, and performed a single Hotelling's T2 test2 for consistency with zero. We reject the null hypothesis at high significance (P = 2 × 10−7), suggesting that the analyzed Native American populations do not all descend from a homogeneous ancestral population since separation from the Outgroups (Extended Data Table 1, SI 2). The coefficients for which non-American populations contribute the most to the signals separate Native Americans into a cline with two Amazonian groups (Suruí and Karitiana) on one extreme and Mesoamericans on the other (Extended Data Figure 2). Among the Outgroups, the most similar coefficients to Amazonian groups are found in Australasian populations: the Onge from the Andaman Islands in the Bay of Bengal (a so-called ‘Negrito’ group), New Guineans, Papuans, and indigenous Australians (SI 2).
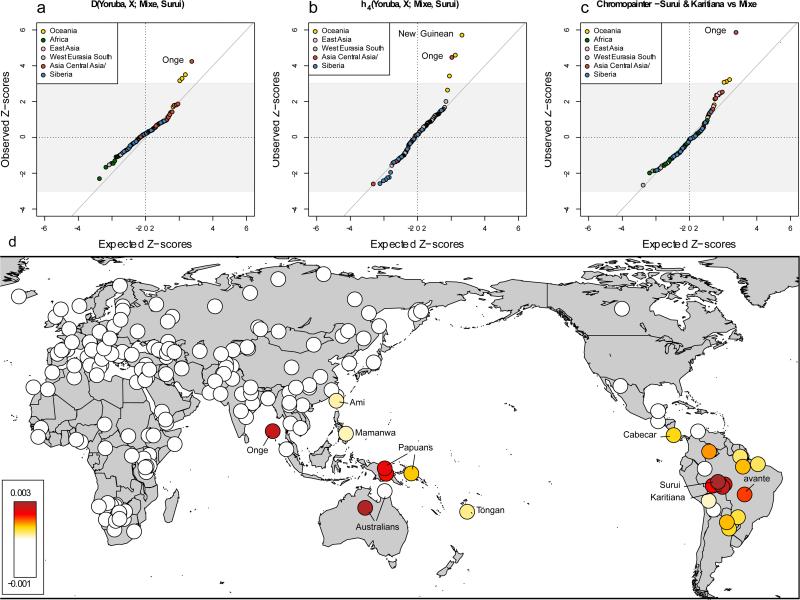
We extended our analysis to 197 non-American populations sampled worldwide18-20. We computed _D_-statistics21 to test whether a randomly drawn derived allele from each worldwide population has an equal probability of matching a randomly drawn Mesoamerican or Amazonian chromosome at sites where these differ. In other words, we take as our null hypothesis the tree-like population history (Test population, (Mesoamericans, Amazonians)), and expect positive _D_-statistics only in the case of excess affinity between the test population and Amazonians (negative values in the case of an affinity with Mesoamericans). Consistent with the signals observed when all populations are analyzed together, we find that Andamanese Onge, Papuans, New Guineans, indigenous Australians and Mamanwa Negritos from the Philippines all share significantly more derived alleles with the Amazonians (4.6 > Z > 3.0 standard errors from zero) (Extended Data Table 2). No population shares significantly more derived alleles with the Mesoamericans than with the Amazonians. We find consistent results for this test not only for Onge, Papuans, New Guineans and indigenous Australians as representatives of Australasian populations, but also for different Outgroups in place of chimpanzee: Africans, Europeans and East Asians (2.8 < Z < 4.8) (SI 3). In Figure 1, we show a quantile-quantile plot of _D_-statistics contrasting the Mesoamerican Mixe and the Amazonian Suruí, revealing Australasian populations as the only discernible outliers.
Figure 1. South Americans share ancestry with Oceanian populations that is not seen in Mesoamericans or North Americans.
a) Quantile-quantile plot of the _Z_-scores for the _D_-statistic symmetry test for whether Mixe and Suruí share an equal rate of derived alleles with a candidate non-American population X, compared to the expected ranked quantiles for the same number of normally distributed values. b) _Z_-scores for the _h_4-statistic. c) _Z_-scores for the CHROMOPAINTER statistic. D) heatmap of CHROMOPAINTER statistics. For non-Americans we display the symmetry statistic S(non-American; Mixe, Suruí & Karitiana) for donating as many haplotypes to Mixe as to Suruí & Karitiana. For the Americas we plot S(Onge; Mixe, American) for receiving as many haplotypes from the Onge as do the Mixe.
We replicated the significant evidence for affinity between Australasians and Amazonians using _D_-statistics computed on Illumina SNP array data2 (as an alternative to Human Origins data) (2.6 < _Z_ < 3.0) and on high coverage genome sequences from 3 Yoruba, 2 Suruí, 3 Mixe, and 16 Papuans (18 of these genomes are reported for the first time here22,23; Table 1) (_Z_ = 4.3). In addition to the three independent molecular experiments that these data sets represent, we find consistent results for all different mutation classes in the high-coverage genomes (2.6 < _Z_ < 4.3), and different ascertainment schemes (_e.g._ in polymorphisms discovered in Africans, New Guineans, and East Asians) (SI 3) (1.1 < _Z_ < 3.3 for panels with >20,000 SNPs). We also find consistent results for two differently genotyped subsets of Suruí individuals from a total of 24 individuals2 (Table 1; Extended Data Figure 3A) (2.6 < Z < 3.6). Simulations (SI 3) show that genotype and sequence errors cannot explain the magnitude of the observed signal (Extended Data Figure 3B). Finally, we generated new data from 9 populations from present-day Brazil using the Affymetrix Human Origins array, including previously untested individuals from the Amazonian Suruí and Karitiana for which DNA was extracted from blood. These new samples replicate the signal, and furthermore show that the signal is also strong in the Xavante (1.3 < Z < 3.25), a population of the Brazilian Central Plateau that speaks a language of the Ge group that is different from the Tupi language group to which the languages that the Karitiana and Suruí speak both belong. We do not detect any excess affinity to Australasians in the ~12,600 year old Clovis-associated Anzick individual from Western Montana (Z = −0.6) (SI 3).
Table 1.
Statistics testing the consistency of the tree (Yoruba, (Papuan, (Mixe, Suruí)) with the data
| Test statistic | _Z_-score | Informative loci | |
|---|---|---|---|
| High-coverage genomes | 0.0211 | 4.26 | 798,873 |
| A/T SNPs | 0.0169 | 2.63 | 60,538 |
| A/G SNPs | 0.0191 | 3.64 | 268,962 |
| A/C SNPs | 0.0208 | 3.49 | 67,210 |
| G/T SNPs | 0.0248 | 4.27 | 67,623 |
| C/T SNPs | 0.0220 | 4.24 | 270,133 |
| C/G SNPs | 0.0248 | 4.26 | 64,951 |
| Illumina array - Surui samples from HGDP | 0.0076 | 2.63 | 247,814 |
| Illumina array - Surui samples not included in HGDP | 0.0081 | 3.02 | 249,941 |
| Affymetrix Human Origins array (Surui cell lines) | 0.0099 | 3.63 | 318,544 |
| Affymetrix Human Origins array (Surui blood samples) | 0.0072 | 2.57 | 313,349 |
| _h_4-statistic (Affymetrix Yoruba ascertainment) | 0.0003 | 4.60 | 14,938 |
| Chromosome painting symmetry test | 0.0026 | 5.26 | - |
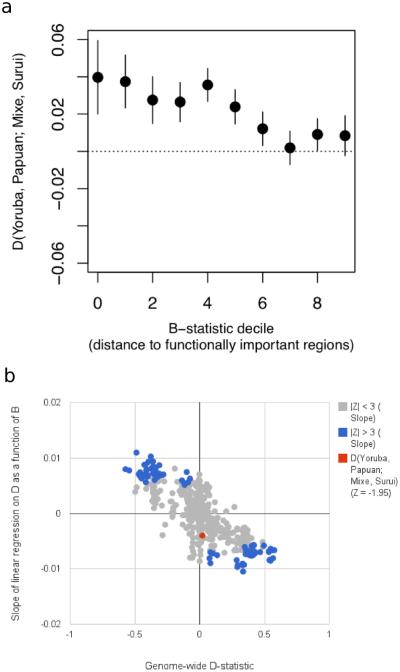
To test if the significant _D_-statistics have the patterns expected for a genuine admixture event, we stratified the high coverage genomes into deciles of ‘_B_-values’24, which measures proximity to functionally important regions. Genuinely significant _D_-statistics are expected to be of larger magnitude closer to genes, since selection increases variability in fitness of haplotypes near functionally important regions, which in turn increases the genetic drift in these regions and the absolute magnitude of _D_-statistics25,26, a prediction that we confirmed empirically (Extended Data Figure 3B). We computed D(Yoruba, Papuan; Mixe, Suruí) separately for each bin, and found that it is of larger magnitude close to functionally important regions (Extended Data Figure 3) (Z = 2.0 for the slope of a linear regression model), as expected for a real admixture event. A caveat is that when we formally combine the evidence from the genome-wide _D_-statistic and the correlation to _B_-value, the significance (Z = 3.6 standard errors from 0) is not any greater than for the basic D = 0.021 ± 0.005 statistic (Z = 4.2 standard errors from 0) because the two statistics co-vary. Nevertheless, the fact that the correlation with _B_-values is significant by itself and in the expected direction adds to the qualitative evidence for an admixture event.
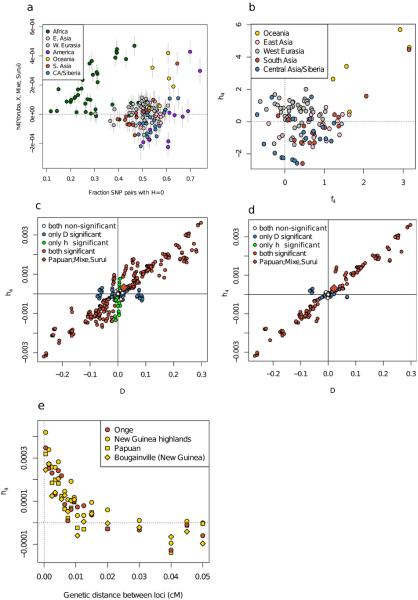
Alternative approaches for testing for admixture involve detecting admixture linkage disequilibrium (LD) in a test population that is correlated to allele frequency differentiation between two populations that are related to the sources27,28. We devised a statistic ‘_h_4’ that is analogous to an _f4_-statistic, but instead of studying allele frequencies, tests whether the LD patterns of two populations are consistent with descending from a common ancestral population since separation from two outgroups. A classical statistic for measuring LD in a population A is HA=p12A−p1Ap2A, which measures the extent to which a haplotype of two derived mutations occurring at frequency p12A is observed more or less frequently than would be expected from the individual frequencies of allele 1 and 2 (p1A and p2A). Thus, we define h4(A, B; C, D) as the average of (HA-HB)(HC-HD) across the genome, and view a deviation from zero as evidence against the unrooted tree ((A, B), (C, D)). We used loci ascertained as polymorphic in African Yoruba, which is effectively an outgroup to the other populations analyzed here, to test _h_4(Yoruba, X; Mixe, Suruí) for all SNP pairs within 0.01cM and for a large set of worldwide non-African populations, and obtained normalized _Z_-scores by estimating the number of standard errors this quantity is from zero using a Block Jackknife. While _Z_-scores computed for most of 120 non-American and non-Africans as population X conform to a normal distribution (Figure 2A), we again find significant evidence of excess affinity of the Suruí to Australasian populations (Z = 5.7, P << 10−5 for New Guineans and Papuans, Z = 4.4, P = 10−5 for Andamanese). When we exclude the Australasians, we detect no evidence of correlation between _Z_-transformed _h_4- and _f_4-statistics for the remaining 114 populations (R = −0.026) suggesting that _h_4 can provide evidence independent of allele frequency based statistics. While _h_4 can in theory be biased by loss of polymorphism due to bottlenecks (SI 4), there is no evidence that this is a problem for our analysis as East Asian and Siberian populations with comparable loss of polymorphism do not show an affinity to Amazonians by this statistic (Extended Data Figure 4). In addition, there is a high degree of correlation between significant _h_4- and _D_-statistics in empirical data (Extended Data Figure 5). Computing _h_4(Yoruba, Onge; Mixe, Suruí) over windows of increasingly large genetic distances reveals that it dissipates at approximately 0.2 cM. This is an order of magnitude smaller than LD caused by admixture events at the ~4,000 year upper limit of previous methods18, but at a larger scale than the signal of admixture between Neanderthals and non-Africans 37,000-86,000 years ago29 (Extended Data Figure 5D).
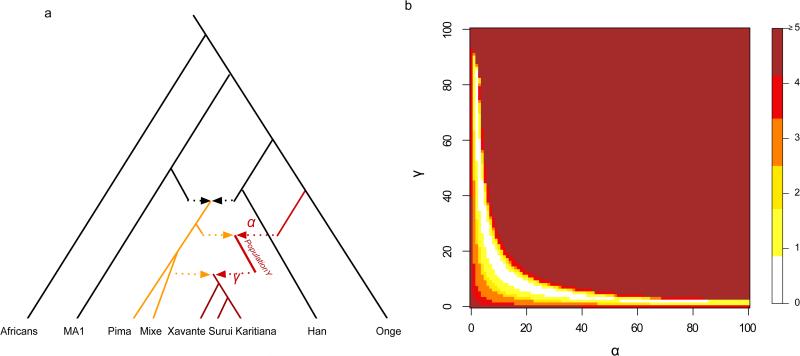
Figure 2.
A model of population history that can explain the excess affinity to Oceanians observed in Amazonian populations. We fit an admixture graph model illustrated in a) where a population related to the Andamanese Onge contributed a fraction α of the ancestry of ‘Population Y’, which later contributed a fraction γ to the ancestry of Amazonian groups today (the remainder of which is related to Mesoamerican Mixe). B) two-dimensional grid of combinations of the admixture proportions α and γ which are compatible with the data in the sense of how many predicted _f_4-statistics deviate by Z ≥3.0 from empirical values. The cross represents the parameter combination fitted heuristically using ADMIXTUREGRAPH.
As a third population symmetry test, we applied a method for detecting shared haplotypes between individuals (‘chromosome painting30) to infer for each SNP in each Native American individual which non-American chromosome segment it shares the closest affinity to, using a set of 174 non-American populations as references. We then performed a symmetry test for a candidate population sharing more haplotypes with a given non-American population than the Mesoamerican Mixe, performing a Block Jackknife across all chromosomes (weighting to correct for variation in chromosome length) to assess uncertainty. We find that the blood and cell line Suruí are significantly closer to the Onge than the Mixe are (Z = 5.3) (Figure 1C), as are the blood and cell line Karitiana samples (Z = 4.2 to 5.0), the Xavante (Z = 4.3), and the Piapoco and Guarani (Z > 3) (Figure 1D). In contrast, populations from west of the Andes or north of the Panama isthmus show no significant evidence of an affinity to the Onge (Z < 2). An exception to this is the Cabecar, who have previously been shown to be partially admixed from a source south of the Panama isthmus2.
The geographic distribution of the shared genetic signal between South Americans and Australasians cannot be explained by post-Columbian African, European or Polynesian gene flow into Native American populations. If such gene flow produced signals strong enough to impact our statistics, our statistics would show their strongest deviations from zero for African, European or Polynesian populations, which is not observed. For example, a direct test is significant in showing that the Suruí-specific ancestry component is genetically closer to the Andamanese Onge than to Tongans from Polynesia (D = 0.0094, Z = 3.4).
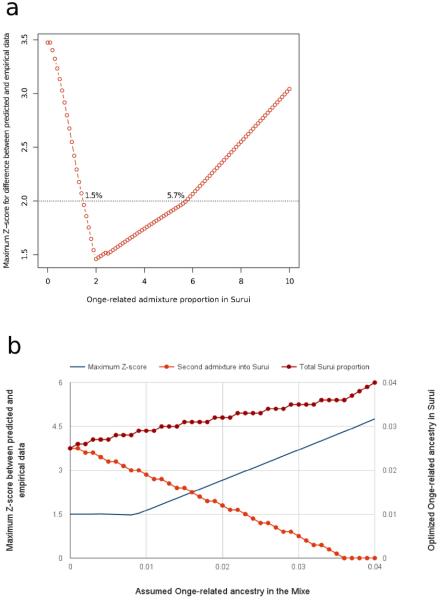
To investigate models consistent with the data, we used the ADMIXTUREGRAPH software to fit admixture graphs relating the ancestry of Native American groups to Han Chinese and Onge Andaman Islanders, incorporating a previously described admixture event into Native American ancestors from a lineage related to a ~24,000 year old Upper Paleolithic individual from Mal'ta in Siberia4. We are unable to fit Amazonians as forming a clade with the Mesoamericans, or as having a different proportion of ancestry related to Mal'ta or present-day East Asians. Thus, our signal cannot be explained by lineages that have previously been documented as having contributed to Native American populations. However, we do find that a model where Amazonians receive ancestry from the lineage leading to the Andamanese fits the data in the sense that its predicted _f_4-statistics are all within 2 standard errors of statistics computed on the empirical data (Extended Data Figure 6; Extended Data Figure 7; Extended Data Table 3). These results do not imply that an unmixed population related anciently to Australasians migrated to the Americas. While this is a formal possibility, an alternative model that we view as plausible is that the ‘Population Y’ (we use ‘Population Y’ after Ypykuéra, which means ‘ancestor’ in the Tupi language family spoken by the Suruí and Kartiana) that contributed Australian related ancestry to Amazonians was already mixed with a lineage related to First Americans at the time it reached Amazonia. When we model such a scenario, we obtain a fit for models that specify 2%-85% of the ancestry of the Suruí, Karitiana, and Xavante as coming from Population Y (Figure 2). These results show that quite a high fraction of Amazonian ancestry today plausibly comes from Population Y. At the same time, the results constrain the fraction of Amazonian ancestry that comes from an Australasian related population (via Population Y) to a much tighter range of 1%-2% (Figure 2).
We have provided compelling evidence that a Population Y that has ancestry from a lineage more closely related to present-day Australasians than to present-day East Asians and Siberians, contributed a small fraction of the DNA of Native Americans from Amazonia and the Central Brazilian Plateau. This discovery is striking in light of interpretations of the morphology of some early Native American skeletons, which some authors have suggested have affinities to Australasian groups. The largest number of skeletons that have been described as having this craniofacial morphology and that date to younger than ten thousand years have been found in Brazil6, the home of the Suruí, Karitiana and Xavante who in genetic data show the strongest affinity to Australasians. However, in the absence of DNA directly extracted from a skeleton with this morphology, our results are not sufficient to conclude that the Population Y we have reconstructed from the genetic data had this morphology.
An open question is when and how Population Y ancestry reached South America. There are several archaeological sites in the Americas that are substantially older than Clovis sites. Since one Clovis site is now known from ancient DNA analysis to have included an individual of entirely First American ancestry3, an interesting hypothesis is that Population Y ancestry may have been prevalent in the individuals of some of these earlier sites. Regardless, our results suggest that at least two different ancestry streams penetrated south of the Late Pleistocene ice sheets, perhaps taking different routes or arriving at different times from a structured Beringian or Northeast Asian source, or reflecting more longstanding gene flow. The genetic data allow us to say with confidence that Population Y ancestry arrived south of the ice sheets anciently: the fact that the geographically diverse Andamanese, Australian and New Guinean populations are all similarly related to this source suggests that the population is no longer extant, and the absence of long-range admixture linkage disequilibrium suggests that the population mixture did not occur in the last few thousand years. Further insight into the population movements responsible for these findings should be possible through genome-wide analysis of ancient remains from across the Americas.
METHODS
New Affymetrix Human Origins genotypes
We generated new Affymetrix Human Origins Array genotypes for 48 individuals from 9 populations from present-day Brazil (Apalaí, Arara, Guarani, Karitiana, Suruí, Urubu Kaapor, Xavante and Zoró). Ethical approval for the sample collection was provided by the Brazilian National Ethics Commission (CONEP Resolution no. 123/98). CONEP also approved the oral consent procedure and the use of these samples in studies of population history and human evolution. Individual and/or tribal informed oral consents were obtained from participants who were not able to read or write. All sampling was coordinated by co-authors of this study (M.L. P.-E. and F.M.S.) and their collaborators, in a manner consistent with the Helsinki Declaration and Brazilian laws and regulations applicable at the time of sampling. Logistical support for the sample collection was provided by the Fundação Nacional do Índio (FUNAI). We curated the data in the same way that was reported in Lazaridis et al. (SI 1). We computationally phased these data together with the previously published Affymetrix Human Origins data using SHAPEIT231 with default parameters.
High coverage genome sequencing and processing
We sent samples from 18 Papuan, Mixe, Suruí and Yoruba individuals to Illumina Ltd. for deep coverage sequencing using a non-PCR-based protocol as part of the Simons Genome Diversity Project. The sequence reads were mapped using the ‘aln’ algorithm of BWA (version 0.5.10)32 and genotypes were inferred using the unified genotyper from GATK33 (version 2.5.2-gf57256b) These data are available from https://www.simonsfoundation.org/life-sciences/simons-genome-diversity-project-dataset/. The processing of the data is described in detail in a manuscript in preparation. Briefly, sequence reads were stripped of adapters prior to alignment to the decoy version of the hg19 reference sequence (hs37d5). Read groups were added for identification and compatibility with GATK tools, before indel realignment and duplicate removal. The genotyping performed thereafter used a reference-free procedure which reduces reference bias. A specially developed filtering engine assigns filtering levels from 0 to 9 for each position in the genome. All population genetic analyses in this paper used the most stringent level of filtering (level 9).
Testing for more than one ancestral population of Central and South Americans
To investigate whether Central and South American populations are consistent with being derived from a single stream of ancestry, we applied qpWave2 to ask the question whether the set of _f_4-statistics of the form _f_4(A = _American_1, B = _American_2; X = _Outgroup_1, Y = _Outgroup_1) = (pA – pB) (pX – pY) forms a matrix that is consistent with being of rank 0 (summed over all SNPs, where _p_A, _p_B, _p_X, and _p_Y are the frequencies of an arbitrarily chosen allele in populations A, B, X and Y at each locus). Intuitively, if all these Native American populations descend from the same stream of migration into the Americas, then the _f_4-statistic relating each Native American population to each non-Native American population should be the same for all Native American populations, and in particular consistent with 0. Formally, to evaluate whether the _f4_-statistic matrix is consistent with being of rank 0, we compute a Hotelling's T2 test that appropriately corrects for the correlation structure of the _f4_-statistics. We analyzed 7 Native American populations each with at least 3 individuals with no detected post-Columbian admixture, and 4 populations from each of 6 worldwide regions as Outgroups (SI 2).
_D_-statistic tests based on correlation in allele frequencies
To investigate whether a tree-like population history ((A, B),(X, Y)) is consistent with the data, for example with A = chimpanzee, B = Onge, X = Mixe and Y = Suruí, we computed _D_-statistics18,21
D(A,B;X,Y)=(pA−pB)(pX−pY)(pA+pB−2pApB)(pX+pY−2pXpY)
over all SNPs, where _p_A, _p_B, _p_X, and _p_Y are the frequencies of an arbitrarily chosen allele in populations A, B, X and Y at each locus. We compute standard errors (SEs) using a Block Jackknife weighted by the number of SNPs in each 5cM (5Mb in the case of high-coverage genome sequences) block in the genome34,35. We report _Z_-scores which are normalized Z= D/SE and we interpret statistics |Z| > 3 as being significantly different from 0. We only considered SNPs that were informative, in the sense that they are polymorphic both within (A,B) and (X,Y).
Correlation of signal to regions of functional importance
We divided the genome into 10 deciles of the ‘_B_-value’ proposed by McVicker et al.24, which integrates multiple genomic annotations into a single estimate of functional importance for each nucleotide in the genome. We then used linear regression to estimated the coefficient a of the function y = ax + c where x = B (the rank of the decile of B) and y = DB (D restricted to the particular decile of B). To compute standard errors, we used a weighted Block Jackknife procedure where each 5 Mb block of the genome is dropped in turn and a is recomputed. The variability of a across each of these leave-1-out computations, weighting by the number of informative loci in each block, is what we use to estimate a standard error34,35
_h_4-statistic tests based on correlation in linkage disequilibrium
We devised a linkage disequilibrium statistic that tests for symmetry in linkage disequilibrium between two proposed clades with a pair of populations in each. The statistic, _h_4, is:
h4=((p12A−p1Ap2A)−(p12B−p1Bp2B))×((p12C−p1Cp2C)−(p12D−p1Dp2D))
where 1 and 2 are arbitrarily chosen references alleles at two different loci, respectively, and A, B, C, and D denote four different populations. Thus, p12A is the frequency of the 12 haplotype in population A, and p1A is the frequency of the 1 allele in population A. The quantity p12A−p1Ap2A thus measures the difference between the observed haplotype frequency and the expected haplotype frequency given the allele frequencies36. The motivation for this statistic being informative about population history is that under a tree-like model ((A, B), (C, D)) with no gene flow, differences in linkage disequilibrium between populations A and B are not expected to correlate to differences in LD between populations C and D. If there has been gene flow between the two clades, the statistic may be significantly positive or negative like _f_4- and _D_-statistics18.
In practice, we computed this statistic for each polymorphic locus (‘target locus’) by identifying all other polymorphic loci 5’ of the target locus at distance interval d_±_w and computing the statistic for each pairing. We then averaged the statistic over all valid pairs of loci in the genome identified in this way. We computed standard errors using a Block Jackknife over contiguous 5cM blocks in the genome, where SNP pairs that bridge the boundary of two blocks are assigned to the block in which the target locus is found. For the main analysis we computed _h_4-statistics of the form _h_4(Yoruba, X; Mixe, Suruí) for all populations X in the Human Origins array, and all pairs of SNPs within 0.01cM of each other. We restricted the analysis to populations with at least 10 individuals. We also computed the _h_4-statistic for windows of 0.001 cM centered around different genetic distances for selected populations (Extended Data Figure 4).
Chromosome-painting symmetry tests
We used SHAPEIT to phase 593,142 SNPs with the same set of individuals as described above, using all panels of SNPs in the Human Origins array. We then ‘painted’ unadmixed Native American individuals using non-American populations, and excluded the Yukagir and the Chukchi since they have evidence of back-migration from the Americas. We ran CHROMOPAINTER v2 using default parameters, painting each recipient individual separately, but using all donor populations as candidates to paint each recipient haplotype. To assess statistical uncertainty, we repeated this procedure for each recipient individual using 22 subsets of the data where for each of these subsets a different chromosome had been dropped. We then used the results of these 22 Block Jackknife pseudo-replicates to obtain a weighted Block Jackknife estimate of the standard error for our test statistic (see below).
To test if the recipient populations copied equally from the donor populations, we computed the average chunk count _C_R:D copied from a given donor population D in each recipient population R (averaged over individuals). We then computed a S(R1, R2; D) statistic that quantifies the symmetry between two Native American populations in their copying from each donor:
S(D;R2,R1)=CR1:D−CR2:DCR1:D+CR2:D
If two Native American populations, such as the Suruí and the Mixe, derive all of their ancestry from a single common origin, we expect that they would copy from the donor populations at an equal rate. We computed the standard error of this statistic using the 22 subsets of the data where each autosome had been dropped, weighted using the number of SNPs on each chromosome. The map displayed in Figure 1D was plotted using the R maps package37.
Admixture Graph models of population relationships
We used ADMIXTUREGRAPH18,35 to fit suggested phylogenies with admixture events to the data. We assessed goodness-of-fit by investigating all possible _f_-statistics predicted by the fitted model and assessing whether they differed significantly from the empirical data. We chose as a starting point the model relating Mbuti Africans, Andamanese Onge, MA1 and Karitiana fitted by a previous study19 where lineages related to MA1 and the Onge both contributed ancestry to the Karitiana. We added to this Han Chinese to represent a population that is phylogenetically more closely related to one of the ancestral populations of Native Americans than are the Onge (Extended Data Figure 6; Extended Data Figure 7). We find that this model is inconsistent with the data, since the model predicts that Mixe and Suruí/Karitiana are equally related to Onge, and indeed we observe several statistics for which the Z-score for the difference between the predicted and empirical statistics is |Z| > 3 (Extended Data Table 3). To account for this, we fitted a model in which the ancestors of Amazonians received admixture from a population related to the Onge (Extended Data Figure 6B), and found that this provided an excellent fit to the data, with no |Z|-score differences greater than 3. In contrast, alternative models of Han-related or MA1-related gene flow into the Americas are inconsistent with the data (Extended Data Figure 6, Extended Data Table 3).
Code availability
A python program for computing _h_4 symmetry statistics and other population genetic statistics used in this paper is available at https://github.com/pontussk/popstats.
Extended Data
Extended Data Figure 1.
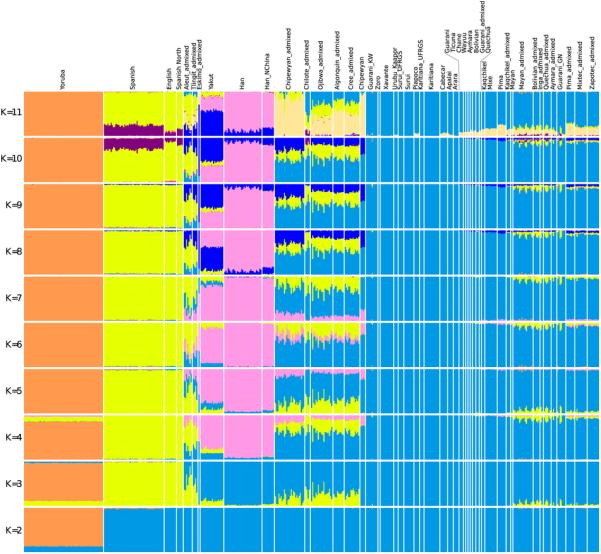
ADMIXTURE38 clustering analysis performed on the Affymetrix Human Origins data used in this study.
Extended Data Figure 2.
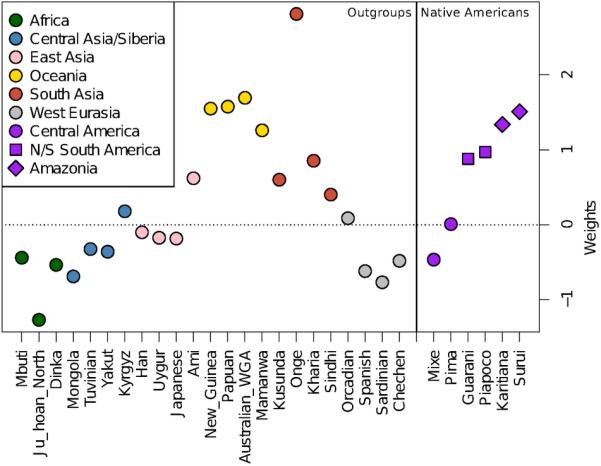
Weights from qpWave for Native Americans and non-American outgroups. No weights are given for Yoruba and Cabecar, as they are used in the computation.
Extended Data Figure 3.
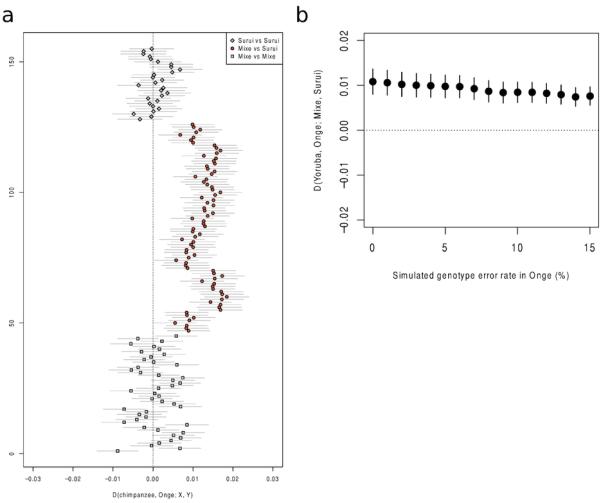
A) Tests for excess shared derived alleles with the Onge in all possible comparisons of 8 Suruí and 10 Mixe individuals. All Mixe-Suruí comparisons show a positive skew whereas all Mixe-Mixe and Suruí-Suruí comparisons are consistent with 0. Lines correspond to 1 standard error in either direction. B) Random sequence or genotype errors cannot explain the affinity of the Amazonians to Australasians, since simulated increased errors in the Onge do not cause an increased affinity to Suruí.
Extended Data Figure 4.
Signals of admixture as a function of proximity to functional regions. A) The affinity of 16 Papuan high-coverage genomes to 2 Amazonian Suruí high-coverage genomes as a function of proximity to regions of functional importance (measured by _B_-value). B) 395 tests of quartets D(Yoruba, X; Y, Z) shows that quartets with significantly positive slopes (|Z| > 3) also yield significant genome-wide _D_-statistics of the opposite sign. This suggests that signals of admixture are systematically stronger close to functionally important regions.
Extended Data Figure 5.
A) _h_4(Yoruba, X; Mixe, Suruí) for SNP pairs within 0.01cM of each other contrasted with the fraction of SNP pairs in linkage equilibrium in population X (H = 0). Bars give ±1 standard error. B) Scatterplot of _Z_-scores for the _f_4- and _h_4-statistics for the same quartets. For both these panels we only use populations with at least 6 samples. C) and D) We computed D(Yoruba, X; Y, Z) and _h_4(Yoruba, X; Y, Z) for many combinations of populations as X, Y and Z using phased Affymetrix Human Origins SNP array data ascertained in a Yoruba individual. Except for Africans who have ancestry from lineages that diverged before the Yoruba used for ascertainment and Oceanians (who have archaic Denisovan ancestry) we observe that |Z|>3 _h_4-statistics are always associated with a significantly positive D for the same quartet. E) Correlation of the _h_4-statistic with the genetic distance separation of pairs of SNPs for _h_4(Yoruba, X; Mixe, Suruí).
Extended Data Figure 6.
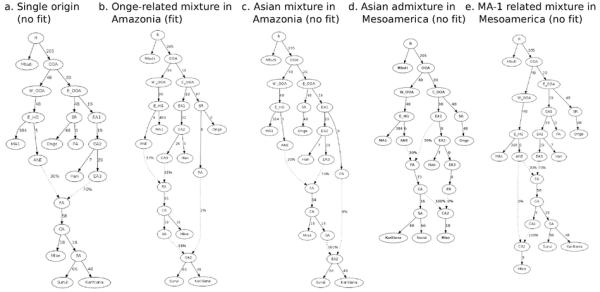
Admixture Graphs (AGs) for fitted population history models. A) An AG where all of Mixe, Suruí, and Karitiana are of 100% First American ancestry is rejected with 6 predicted _f_-statistics at least 3 SEs from the empirically observed value. B) An AG where the ancestors of Suruí and Karitiana receive 2% ancestry from a lineage related to the Onge is consistent with the data with no outliers. C) An AG where the distinct ancestry in Amazonians is more closely related to Han than to Onge produces 6 outliers. D) An AG with no distinctive ancestry in Karitiana or Suruí but East Asian gene flow into the Mixe produces 7 outliers. E) An AG with no distinctive ancestry in Karitiana or Suruí but MA1-related gene flow into the Mixe produces 6 outliers.
Extended Data Figure 7.
Plausible range for the non-First American admixture proportion in Amazonians. A) Range obtained assuming entirely First American ancestry in the Mixe. B) The maximum proportion of non-First American ancestry in the Mixe that is consistent with the data.
| _P_-value for this number of streams | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Full data | 2.03E-07 | 0.09 | 0.58 | 0.92 |
| Outgroup region dropped | ||||
| Africa | 1.67E-04 | 0.34 | 0.92 | 0.95 |
| C. Asia/Siberia | 5.91E-07 | 0.11 | 0.6 | 0.89 |
| East Asia | 4.46E-09 | 0.04 | 0.57 | 0.92 |
| South Asia | 6.95E-05 | 0.1 | 0.4 | 0.82 |
| West Eurasia | 1.41E-05 | 0.06 | 0.37 | 0.89 |
| Oceania | 4.39E-05 | 0.43 | 0.88 | 0.97 |
| Native American population dropped | ||||
| Cabecar | 1.13E-08 | 0.02 | 0.27 | 0.73 |
| Guarani | 9.50E-07 | 0.27 | 0.76 | 0.99 |
| Karitiana | 1.41E-06 | 0.1 | 0.61 | 0.86 |
| Mixe | 8.32E-03 | 0.2 | 0.91 | 0.98 |
| Piapoco | 1.30E-04 | 0.55 | 0.93 | 0.98 |
| Pima | 2.19E-05 | 0.31 | 0.78 | 0.97 |
| Surui | 2.35E-06 | 0.11 | 0.56 | 0.84 |
| Africa + 1 other region | ||||
| Siberia | 0.16 | 0.56 | 0.8 | 0.87 |
| East Asia | 0.06 | 0.29 | 0.71 | 0.72 |
| South Asia | 0.004 | 0.57 | 0.93 | 0.96 |
| West Eurasia | 0.02 | 0.23 | 0.62 | 0.67 |
| Oceania | 0.01 | 0.25 | 0.82 | 0.99 |
| Siberia + 1 other region | ||||
| Africa | 0.16 | 0.56 | 0.8 | 0.87 |
| East Asia | 0.41 | 0.91 | 0.99 | 1 |
| South Asia | 0.03 | 0.82 | 0.91 | 0.9 |
| W. Eurasia | 0.2 | 0.59 | 0.77 | 0.83 |
| Oceania | 0.003 | 0.18 | 0.75 | 0.93 |
Extended Data Table 2.
Top 20 _D_-statistics observed for D(chimpanzee, Old World population; Central Americans, Amazonians).
| Rank | Population | D | SE | Z | Region 1 | Region 2 |
|---|---|---|---|---|---|---|
| 1 | Onge | 0.0101 | 0.0022 | 4.60 | India | South Asia |
| 2 | Papuan | 0.0084 | 0.0022 | 3.82 | Papua New Guinea | Oceania |
| 3 | New_Guinea | 0.0082 | 0.0023 | 3.54 | Papua New Guinea | Oceania |
| 4 | Australian_WGA | 0.0074 | 0.0024 | 3.12 | Australia (Arnhem Land) | Oceania |
| 5 | Mamanwa | 0.0068 | 0.0020 | 3.40 | Philippines (Negrito) | Oceania |
| 6 | Bougainville | 0.0065 | 0.0023 | 2.85 | Papua New Guinea | Oceania |
| 7 | Kharia | 0.0059 | 0.0020 | 2.97 | India | South Asia |
| 8 | Tongan | 0.0058 | 0.0022 | 2.68 | Tonga | Oceania |
| 9 | Bengali | 0.0058 | 0.0019 | 3.00 | Bangladesh | South Asia |
| 10 | Mala | 0.0055 | 0.0019 | 2.93 | India | South Asia |
| 11 | Ami | 0.0052 | 0.0020 | 2.61 | Taiwan | East Asia |
| 12 | Lodhi | 0.0052 | 0.0019 | 2.72 | India | South Asia |
| 13 | Sindhi | 0.0051 | 0.0019 | 2.72 | Pakistan | South Asia |
| 14 | Kusunda | 0.0050 | 0.0020 | 2.56 | Nepal | South Asia |
| 15 | Lahu | 0.0050 | 0.0021 | 2.37 | China | East Asia |
| 16 | Kinh | 0.0049 | 0.0020 | 2.46 | Vietnam | East Asia |
| 17 | Australian | 0.0048 | 0.0025 | 1.96 | Australia | Oceania |
| 18 | Balochi | 0.0047 | 0.0019 | 2.55 | Pakistan | South Asia |
| 19 | Thai | 0.0047 | 0.0020 | 2.38 | Thailand | East Asia |
| 20 | Semende | 0.0045 | 0.0020 | 2.27 | Indonesia (Sumatra) | Oceania |
Extended Data Table 3.
_f_4-statistics for which the statistic predicted by the fitted admixture graphs deviates by more |Z| > 3 from the statistic computed on the empirical data.
| A | B | X | Y | Predicted _f_4 | Empirical _f_4 | _Z_-score |
|---|---|---|---|---|---|---|
| Single First American origin (Extended Data Figure 6A) | ||||||
| Mbuti | Onge | Mixe | Surui | 0 | 0.003506 | 3.535 |
| Mbuti | Onge | Mixe | Karitiana | 0 | 0.00315 | 3.431 |
| Onge | Mixe | Mixe | Surui | −0.018466 | −0.021724 | −3.061 |
| Onge | Mixe | Mixe | Karitiana | −0.018466 | −0.021849 | −3.226 |
| Onge | Han | Mixe | Surui | 0 | −0.002902 | −3.654 |
| Onge | Han | Mixe | Karitiana | 0 | −0.00239 | −3.279 |
| Paleoamerican ancestry in the Amazon (Extended Data Figure 6B) | ||||||
| (No outliers) | ||||||
| East Asian admixture in South America (Extended Data Figure 6C) | ||||||
| Mbuti | Onge | Mixe | Surui | 0 | 0.003506 | 3.535 |
| Mbuti | Onge | Mixe | Karitiana | 0 | 0.00315 | 3.431 |
| Onge | Mixe | Mixe | Surui | −0.018466 | −0.021724 | −3.061 |
| Onge | Mixe | Mixe | Karitiana | −0.018466 | −0.021849 | −3.226 |
| Onge | Han | Mixe | Surui | 0 | −0.002902 | −3.654 |
| Onge | Han | Mixe | Karitiana | 0 | −0.00239 | −3.279 |
| East Asian admixture in Central America (Extended Data Figure 6D) | ||||||
| Mbuti | Onge | Mixe | Surui | −0.000002 | 0.003506 | 3.537 |
| Mbuti | Onge | Mixe | Karitiana | −0.000002 | 0.00315 | 3.433 |
| Onge | Mixe | Mixe | Surui | −0.018466 | −0.021724 | −3.061 |
| Onge | Mixe | Mixe | Karitiana | −0.018466 | −0.021849 | −3.225 |
| Onge | Han | Mixe | Surui | −0.000004 | −0.002902 | −3.649 |
| Onge | Han | Mixe | Karitiana | −0.000004 | −0.00239 | −3.273 |
| Ancient Siberian (MA1) admixture in Central America (Extended Data Figure 6E) | ||||||
| Mbuti | Onge | Mixe | Surui | 0 | 0.003506 | 3.535 |
| Mbuti | Onge | Mixe | Karitiana | 0 | 0.00315 | 3.431 |
| Onge | Mixe | Mixe | Surui | −0.018470 | −0.021724 | −3.057 |
| Onge | Mixe | Mixe | Karitiana | −0.018470 | −0.021849 | −3.222 |
| Onge | Han | Mixe | Surui | 0 | −0.002902 | −3.654 |
| Onge | Han | Mixe | Karitiana | 0 | −0.00239 | −3.279 |
Supplementary Material
supp_info
ACKNOWLEDGEMENTS
We are grateful to the Brazilian volunteers who contributed their DNA samples that were used to generate the new data reported in this study and to the Fundação Nacional do Índio (FUNAI, Brazil) for logistical support. We thank Bill Klitz and Cheryl Winkler for sharing samples for whole-genome sequencing. We thank Lars Fehren-Schmitz, Qiaomei Fu, Garrett Hellenthal, Alexander Kim, Iosif Lazaridis, Mark Lipson, Iain Mathieson, David Meltzer, Priya Moorjani, and Joe Pickrell for critical comments, and Arti Tandon for technical assistance. We thank Tiago Ferraz and Rafael Bisso-Machado for assistance with DNA extraction for the new genotyping of Brazilian samples. We performed whole genome sequencing as part of the Simons Genome Diversity Project. Genotyping of the new Brazilian samples was performed at the Children's Hospital of Philadelphia, and we thank Cuiping Hou for her work to obtain high quality results with the degraded DNA in these samples. M.C.B., T.H., M.L.P.-E. and F.M.S. were supported by Conselho Nacional do Desenvolvimento Científico e Tecnológico and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Brazil). PS was supported by the Wenner-Gren foundation and the Swedish Research Council (VR grant 2014-453). DR was supported by U.S. National Science Foundation HOMINID grant BCS-1032255, U.S. National Institutes of Health grant GM100233, Simons Foundation Grant 280376, and the Howard Hughes Medical Institute.
Footnotes
AUTHOR CONTRIBUTIONS
P.S. performed analyses. P.S., S.M., M.C.B., N.C., T.H., M.L.P-E, F.M.S., N.P. and D.R. prepared datasets. P.S. and D.R. wrote the paper.
The authors declare no competing financial interests.
References
- 1.Wang S, et al. Genetic Variation and Population Structure in Native Americans. PLoS Genet. 2007;3:e185. doi: 10.1371/journal.pgen.0030185. doi:10.1371/journal.pgen.0030185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Reich D, et al. Reconstructing Native American population history. Nature. 2012;488:370–374. doi: 10.1038/nature11258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rasmussen M, et al. The genome of a Late Pleistocene human from a Clovis burial site in western Montana. Nature. 2014;506:225–229. doi: 10.1038/nature13025. doi:10.1038/nature13025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Raghavan M, et al. Upper Palaeolithic Siberian genome reveals dual ancestry of Native Americans. Nature advance online publication. 2013 doi: 10.1038/nature12736. doi:10.1038/nature12736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Neves W, Pucciarelli H. American Journal of Physical Anthropology. WILEY-LISS DIV JOHN WILEY & SONS INC; 605 THIRD AVE, NEW YORK, NY 10158-0012: pp. 274–274. [Google Scholar]
- 6.Neves W, et al. Early Holocene human skeletal remains from Cerca Grande, Lagoa Santa, Central Brazil, and the origins of the first Americans. World Archaeology. 2004;36:479–501. [Google Scholar]
- 7.Neves WA, Prous A, González-José R, Kipnis R, Powell J. Early Holocene human skeletal remains from Santana do Riacho, Brazil: implications for the settlement of the New World. Journal of Human Evolution. 2003;45:19–42. doi: 10.1016/s0047-2484(03)00081-2. [DOI] [PubMed] [Google Scholar]
- 8.González-José R, et al. Late Pleistocene/Holocene craniofacial morphology in Mesoamerican Paleoindians: implications for the peopling of the New World. American journal of physical anthropology. 2005;128:772–780. doi: 10.1002/ajpa.20165. [DOI] [PubMed] [Google Scholar]
- 9.Rasmussen M, et al. Ancient human genome sequence of an extinct Palaeo-Eskimo. Nature. 2010;463:757–762. doi: 10.1038/nature08835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Raghavan M, et al. The genetic prehistory of the New World Arctic. Science. 2014;345 doi: 10.1126/science.1255832. doi:10.1126/science.1255832. [DOI] [PubMed] [Google Scholar]
- 11.Gilbert MTP, et al. DNA from pre-Clovis human coprolites in Oregon, North America. Science. 2008;320:786–789. doi: 10.1126/science.1154116. [DOI] [PubMed] [Google Scholar]
- 12.Chatters JC, et al. Late Pleistocene Human Skeleton and mtDNA Link Paleoamericans and Modern Native Americans. science. 2014;344:750–754. doi: 10.1126/science.1252619. [DOI] [PubMed] [Google Scholar]
- 13.Jantz RL, Owsley DW. Variation among early North American crania. American Journal of Physical Anthropology. 2001;114:146–155. doi: 10.1002/1096-8644(200102)114:2<146::AID-AJPA1014>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 14.Neves WA, Hubbe M, Correal G. Human skeletal remains from Sabana de Bogota, Colombia: a case of Paleoamerican morphology late survival in South America? American journal of physical anthropology. 2007;133:1080–1098. doi: 10.1002/ajpa.20637. [DOI] [PubMed] [Google Scholar]
- 15.Gonzalez-Jose R, et al. Craniometric evidence for Palaeoamerican survival in Baja California. Nature. 2003;425:62–65. doi: 10.1038/nature01816. [DOI] [PubMed] [Google Scholar]
- 16.Sparks CS, Jantz RL. A reassessment of human cranial plasticity: Boas revisited. Proceedings of the National Academy of Sciences. 2002;99:14636–14639. doi: 10.1073/pnas.222389599. doi:10.1073/pnas.222389599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Relethford JH. Apportionment of global human genetic diversity based on craniometrics and skin color. American Journal of Physical Anthropology. 2002;118:393–398. doi: 10.1002/ajpa.10079. doi:10.1002/ajpa.10079. [DOI] [PubMed] [Google Scholar]
- 18.Patterson N, et al. Ancient admixture in human history. Genetics. 2012;192:1065–1093. doi: 10.1534/genetics.112.145037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lazaridis I, et al. Ancient human genomes suggest three ancestral populations for present-day Europeans. Nature. 2014;513:409–413. doi: 10.1038/nature13673. doi:10.1038/nature13673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qin P, Stoneking M. Denisovan Ancestry in East Eurasian and Native American Populations. Molecular Biology and Evolution. 2015 doi: 10.1093/molbev/msv141. doi:10.1093/molbev/msv141. [DOI] [PubMed] [Google Scholar]
- 21.Green RE, et al. A Draft Sequence of the Neandertal Genome. Science. 2010;328:710–722. doi: 10.1126/science.1188021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Meyer M, et al. A High-Coverage Genome Sequence from an Archaic Denisovan Individual. Science. 2012;338:222–226. doi: 10.1126/science.1224344. doi:10.1126/science.1224344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Prufer K, et al. The complete genome sequence of a Neanderthal from the Altai Mountains. Nature. 2014;505:43–49. doi: 10.1038/nature12886. doi:10.1038/nature12886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McVicker G, Gordon D, Davis C, Green P. Widespread genomic signatures of natural selection in hominid evolution. PLoS genetics. 2009;5:e1000471. doi: 10.1371/journal.pgen.1000471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gillespie JH. Genetic drift in an infinite population: the pseudohitchhiking model. Genetics. 2000;155:909–919. doi: 10.1093/genetics/155.2.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Coop G, et al. The role of geography in human adaptation. PLoS genetics. 2009;5:e1000500. doi: 10.1371/journal.pgen.1000500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moorjani P, et al. The history of African gene flow into Southern Europeans, Levantines, and Jews. PLoS genetics. 2011;7:e1001373. doi: 10.1371/journal.pgen.1001373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hellenthal G, et al. A Genetic Atlas of Human Admixture History. Science. 2014;343:747–751. doi: 10.1126/science.1243518. doi:10.1126/science.1243518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sankararaman S, Patterson N, Li H, Pääbo S, Reich D. The date of interbreeding between Neandertals and modern humans. PLoS genetics. 2012;8:e1002947. doi: 10.1371/journal.pgen.1002947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lawson DJ, Hellenthal G, Myers S, Falush D. Inference of population structure using dense haplotype data. PLoS genetics. 2012;8:e1002453. doi: 10.1371/journal.pgen.1002453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Delaneau O, Marchini J, Zagury J-F. A linear complexity phasing method for thousands of genomes. Nature methods. 2012;9:179–181. doi: 10.1038/nmeth.1785. [DOI] [PubMed] [Google Scholar]
- 32.Li H, Durbin R. Fast and accurate short read alignment with Burrows–Wheeler transform. Bioinformatics. 2009;25:1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McKenna A, et al. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome research. 2010;20:1297–1303. doi: 10.1101/gr.107524.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Busing FM, Meijer E, Van Der Leeden R. Delete-m jackknife for unequal m. Statistics and Computing. 1999;9:3–8. [Google Scholar]
- 35.Reich D, Thangaraj K, Patterson N, Price AL, Singh L. Reconstructing Indian population history. Nature. 2009;461:489–494. doi: 10.1038/nature08365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Robbins RB. Some applications of mathematics to breeding problems III. Genetics. 1918;3:375. doi: 10.1093/genetics/3.4.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Becker RA, Wilks AR. Maps in S. AT\ &T Bell Laboratories Statistics Research Report [93.2] 1993 [Google Scholar]
- 38.Alexander D, Novembre J, Lange K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009;19:1655–1664. doi: 10.1101/gr.094052.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
supp_info