How curvature-generating proteins build scaffolds on membrane nanotubes (original) (raw)
Significance
Lipid membranes are dynamic assemblies, changing shape on nano- to micron-sized scales. Some proteins can sculpt membranes by organizing into a molecular scaffold, dictating the membrane’s shape and properties. We combine microscopy, mathematical modeling, and simulations to explore how Bin/Amphiphysin/Rvs proteins assemble to form scaffolds on nanotubes. We show that the way protein locally deforms the membrane affects where it will nucleate before making a scaffold. In this process, the protein’s amphipathic helices—which shallowly insert into the membrane—seem dispensable. Surprisingly, the scaffold forms at low protein density on the nanotube. We simulate a structure of protein scaffolds at molecular resolution, shedding light on how these proteins may sculpt the membrane to facilitate important dynamic events in cells.
Keywords: protein scaffold, BAR proteins, membrane curvature, self-assembly, endocytosis
Abstract
Bin/Amphiphysin/Rvs (BAR) domain proteins control the curvature of lipid membranes in endocytosis, trafficking, cell motility, the formation of complex subcellular structures, and many other cellular phenomena. They form 3D assemblies that act as molecular scaffolds to reshape the membrane and alter its mechanical properties. It is unknown, however, how a protein scaffold forms and how BAR domains interact in these assemblies at protein densities relevant for a cell. In this work, we use various experimental, theoretical, and simulation approaches to explore how BAR proteins organize to form a scaffold on a membrane nanotube. By combining quantitative microscopy with analytical modeling, we demonstrate that a highly curving BAR protein endophilin nucleates its scaffolds at the ends of a membrane tube, contrary to a weaker curving protein centaurin, which binds evenly along the tube’s length. Our work implies that the nature of local protein–membrane interactions can affect the specific localization of proteins on membrane-remodeling sites. Furthermore, we show that amphipathic helices are dispensable in forming protein scaffolds. Finally, we explore a possible molecular structure of a BAR-domain scaffold using coarse-grained molecular dynamics simulations. Together with fluorescence microscopy, the simulations show that proteins need only to cover 30–40% of a tube’s surface to form a rigid assembly. Our work provides mechanical and structural insights into the way BAR proteins may sculpt the membrane as a high-order cooperative assembly in important biological processes.
Curvature of lipid membranes plays important roles in the cell. It allows dynamic cellular phenomena, such as trafficking or cell division, and it can also mediate the interactions among many membrane-bound proteins (1, 2). Proteins containing a Bin/Amphiphysin/Rvs (BAR) domain participate in numerous membrane-curving processes, such as endocytosis, trafficking, motility, the formation of T-tubules, cytokinesis, and so on (3, 4). BAR domains are characterized by a crescent shape whose curvature, length, and binding affinity to the membrane are distinct among different members (4–6). Many BAR proteins also contain amphipathic helices that shallowly insert into the bilayer.
BAR proteins generate curvature as a combination of (i) adhesive electrostatic interactions via their BAR domain and (ii) the insertion of amphipathic helices. Additionally, BAR proteins can associate into highly ordered assemblies on the membrane, thus collectively altering its shape and mechanics (7–10). Precisely how they assemble and affect the membrane is argued to depend on the surface density of proteins, membrane tension, and membrane shape (11). On a flat membrane at a low surface density, BAR proteins can form strings and a meshlike network, which can give rise to budding and tubulation (12–16). At a sufficiently high protein density, they affect the mechanical properties of the membrane and stabilize membrane nanotubes (7, 10, 17–20).
An assembly of BAR proteins on cylindrical membranes has so far only been visualized using EM (e.g., refs. 8, 9, and 21). Although these studies provide important and detailed assessments of how BAR domains may interact with one another on curved membranes as a packed protein arrangement, membrane tubules in those experiments were generated typically from highly charged liposomes exposed to very high protein concentrations. In the cell, especially in the context of endocytosis, protein concentration is not high enough to induce appreciable spontaneous tubulation, nor would such a mechanism be beneficial to the cell. Importantly, a tightly packed assembly of BAR proteins would preclude the recruitment of many other proteins required in endocytosis and trafficking.
To achieve close packing, protein–protein interactions were implicated to be important, namely the lateral interactions between neighboring BAR domains in F-BAR proteins (8) or between N-terminal amphipathic helices in N-BAR proteins (9). It is unclear whether BAR proteins in endocytosis and trafficking cooperatively shape the membrane by virtue of specific protein–protein interactions or whether they assemble as a result of a more general membrane-mediated mechanism. Moreover, it is important to understand how BAR proteins assemble at much lower protein surface densities and on membrane compositions that much more likely resemble those found within the cell.
We hypothesize that BAR proteins can oligomerize on a membrane nanotube at densities much lower than close packing owing to membrane-mediated attractions. We refer to this structure as a protein scaffold. It is to be noted that the term “scaffold” is often used to describe a single BAR domain, imprecisely termed the scaffolding domain. Here, a scaffold represents a 3D rigid assembly of multiple proteins that adheres to the membrane and affects the shape and properties of the membrane.
In this work, we combine in vitro reconstitution, fluorescent microscopy, mechanical measurements, and analytical modeling to describe the mechanism by which BAR proteins assemble on membrane nanotubes to form a scaffold. We also demonstrate that rigid protein scaffolds form at much lower surface densities than full packing. We simulate the protein scaffold at molecular resolution using coarse-grained (CG) molecular dynamics (MD).
Finally, because the relative contribution of BAR domain versus amphipathic helices in inducing curvature is still highly debated, we explore how these domains contribute to the scaffold formation. To this end, we tested three proteins with well-distinguished structural features: endophilin A2 (an N-BAR protein containing four amphipathic helices), endophilin A2 mutants, β2-centaurin (a classical BAR domain with no amphipathic helices), and epsin 1 (a protein that binds membranes via an amphipathic helix in its epsin N-terminal homology domain).
Results
Endophilin Scaffold Initiates at the Base of a Tube.
To study the interactions of BAR proteins with a cylindrical membrane, we used a previously developed micromanipulation setup (7). In the experiment, we pull a nanotube from a giant unilamellar vesicle (GUV) using optical tweezers. A nanotube connected to the base membrane is a typical configuration characteristic of some endocytic processes, such as in a clathrin-independent endocytic mechanism mediated by endophilin (22, 23). The vesicle is held by a micropipette whose aspiration pressure sets the membrane tension, implicitly tube radius, in the absence of proteins (24, 25) (SI Methods). Thus, we have a direct control of the initial radius of curvature, which in our case ranges from ∼10 nm to ∼100 nm (7). With another micropipette we inject the protein near the tube, starting from low vesicle tension. The N-BAR domain of the WT endophilin A2 and β2 centaurin (BAR + pleckstrin homology domain) were fluorescently labeled so that we could directly observe their binding to the membrane with confocal microscopy. By measuring the lipid and the protein fluorescence, we can calculate the tube radius and the protein’s surface density, respectively (7) (Fig. S1 and SI Methods). Therefore, at the same time, we observe how proteins affect the shape of the membrane, while controlling membrane tension and membrane curvature.
Fig. S1.
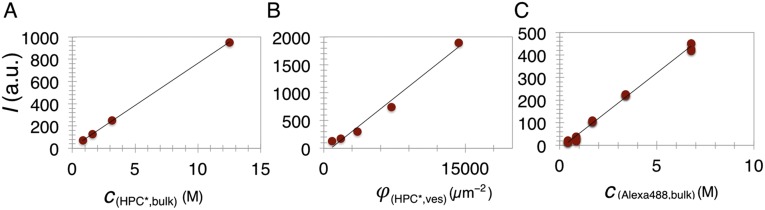
Protein surface density calibration. The HPC* lipid fluorescence intensity scales linearly with its concentration in bulk (A) and in GUVs (B). (C) The fluorescence intensity of Alexa488 (bound to a protein) scales linearly with its bulk fluorescence intensity. The slopes of plots are used to calculate the absolute surface density of proteins. Measurements shown are for specific detection gain and laser power output.
We prepared GUVs using a total lipid brain extract, supplemented with 5% (mol/mol) PI(4,5)P2. Because such a natural composition has not yet been used for quantitative mechanical measurements (26, 27), we confirmed that the membrane curvature scales with GUV tension as theoretically expected for fluid membranes (25) and that these vesicles are not undergoing phase separation (28) (SI Text and Figs. S2 and S3).
Fig. S2.
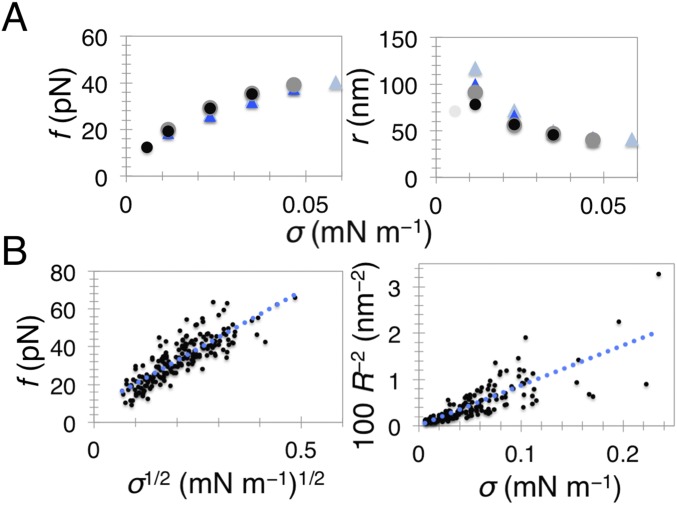
The mechanics of the total lipid brain extract membrane supplemented with 5% PI(4,5)P2. (A) Tube-retraction force f (Left) and tube radius r (Right) as a function of membrane tension, σ, for a single GUV. The experiment was performed by first stepwise increasing σ (black dots) then stepwise decreasing it (gray dots). Then, we injected the experimental buffer first stepwise increasing σ (blue triangles) then again decreasing it (light blue triangles). There is almost complete superposition. Note that in the first radius measurement (light gray dot that deviates) the tube was not in focus. (B) Shown are fits of Eq. S1 (Left) and Eq. S2 (Right) to our data. Number of independent vesicles: 45 (Left) and 36 (Right). Tube radius was measured from the lipid fluorescence.
Fig. S3.
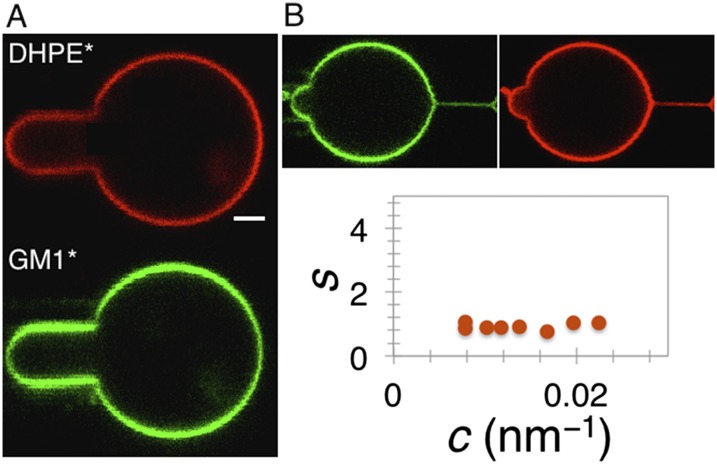
Phase behavior of the membrane. (A) Homogeneous distribution of the lipid dyes in the total lipid brain extract vesicles, indicating no phase separation. (B) The absence of lipid sorting on a curved membrane. Tube radius of curvature, c, is calculated from the force; the sorting, S, is adjusted by the polarization factor. Shown is representative of four different experiments. (Scale bar, 2 µm.)
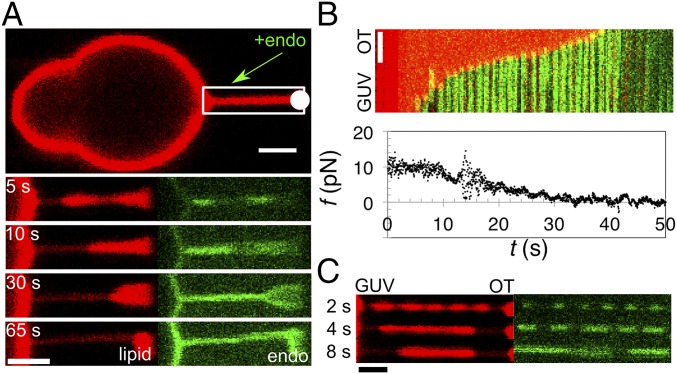
First, we studied how the N-BAR of endophilin A2 (29, 30) (Fig. S4) forms a scaffold on a membrane tube, by injecting the protein at 0.5–2.5 µM (dimeric concentration in the pipette). Note that due to diffusion the concentration of the protein near the GUV is approximately half that in the pipette (31). Endophilin showed a remarkable specificity for the base of a pulled nanotube, binding first either at the interface with the vesicle or with the trapped bead (Fig. 1_A_). Note that the two interfaces are morphologically equivalent, having the same saddle-like membrane geometry. Out of 59 experiments, endophilin first bound to the GUV–tube interface in 53 of them, while also simultaneously binding to the interface with the bead in 27 experiments. In four cases, endophilin seemed to bind homogeneously along the tube where, possibly, the initial binding was not recorded sufficiently fast. Only in the two remaining cases considered as negative the protein first bound to a region other than the interface.
Fig. S4.
X-ray and homology modeling structures of proteins used in the study. (A) Homology modeling of the N-BAR domain of endophilin A2. (B) Homology modeling of BAR and PH domains of β2 centaurin. For A and B, proteins viewed from the side (top) and above the membrane surface (bottom). (C) Endophilin A2 E37K, D41K (mutated residues colored yellow). (D) Crystal structure of the epsin N-terminal homology domain of epsin 1 (PDB ID code 1EDU). Blue and orange color coding based on monomer; red, N-terminal helices and black, PH domain.
Fig. 1.
Scaffolding by endophilin A2. (A) Endophilin A2 N-BAR domain (endo) (amino acids 1–247) binds to the tube’s base and forms a scaffold that continuously grows along the tube [note the progressive constriction in the tube radius from the GUV toward the optical trap (OT, white circle)]. (B) A kymogram of scaffold growth from the GUV to the bead (fluorescence dims near the end as the tube buckles in and out of focus). Lipid and protein channels are overlaid. The plot shows tube-retraction force, f, as a function of time, t. The x axis of the kymogram coincides with the x axis of the plot. (C) Time lapse of a striated pattern induced by endophilin A2 N-BAR domain. t = 0 marks the time when protein was detected on the tube. (All scale bars, 2 μm.)
Shortly after binding, the region covered by endophilin continuously grew along the tube, eventually partially or fully covering it (Fig. 1 A and B; see SI Text for additional statistics). In most cases, the growth of the endophilin scaffold was linear and it ranged from ∼20 nm⋅s−1 to ∼300 nm⋅s−1 (Fig. 1_B_; see also Fig. S5 and Movie S1).
Fig. S5.
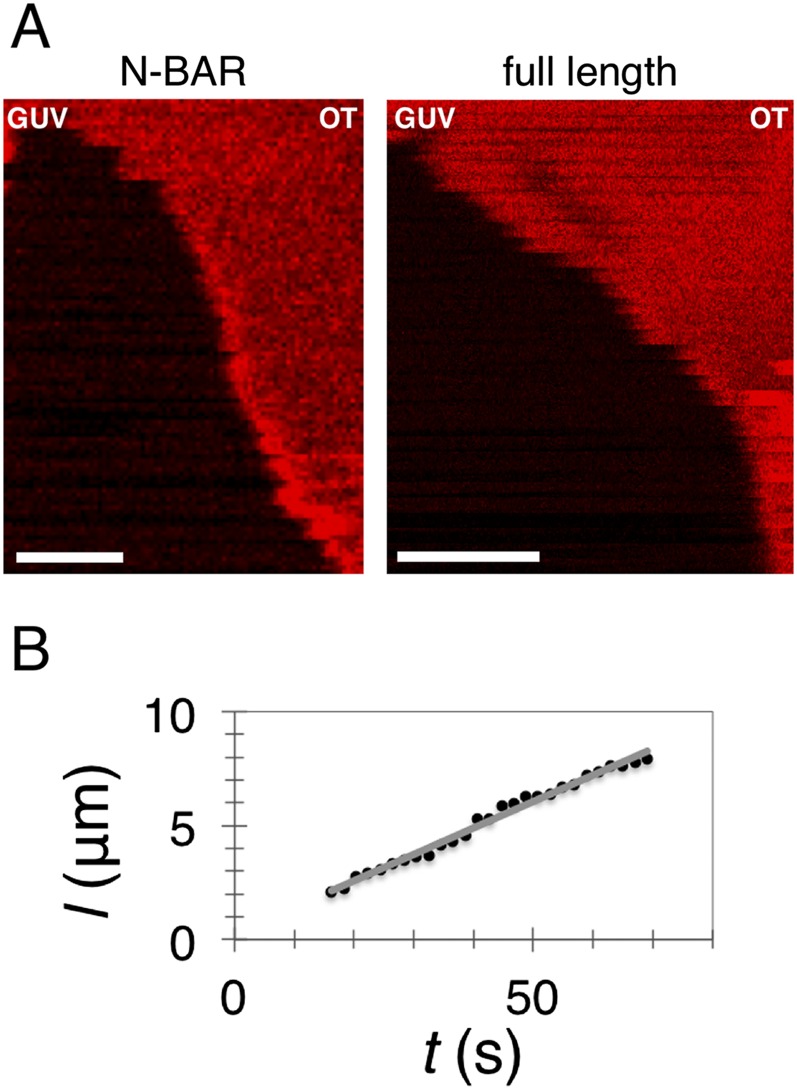
Scaffolding by endophilin A2. (A) Kymograms of membrane tubes scaffolded by full-length endophilin A2 (Right) and N-BAR domain of endophilin A2 (Left). Lipids are fluorescent. The diminishment of fluorescence indicates a constriction of the membrane tube to r ∼10 nm (i.e., the formation of a scaffold). (Scale bars, 2 µm.) (B) An example measuring scaffold length as a function of time; the gray line is a linear fit.
The marked reduction of the lipid fluorescence intensity underneath the protein (Fig. 1_A_, lipid channel) indicates that endophilin changes the tube radius independently of GUV tension. Hence, it forms a stable 3D structure that dictates the membrane curvature. Tube constriction has previously been observed with other members of the BAR family (7, 22, 32), although the dynamics of scaffold formation has not been captured. Binding and constriction under the scaffold are concomitant with the progressive drop in force required to hold the nanotube (Fig. 1_B_). A fully covered tube at low GUV tension imposes no force on the optical trap and undergoes buckling (see the deformation of the tube in the bottom panel of Fig. 1_A_; also see Movie S1). Of note, in the experiments the proteins are also bound to the GUV (see, e.g., Fig. 1_A_).
We observed no difference in the tube-binding behavior between the full-length endophilin A2 (N-BAR + SH3 domain) and only its N-BAR domain, indicating that the location of scaffold initiation is not determined by the protein’s SH3 domain (Fig. S5).
Interestingly, sometimes at higher injected concentrations (>1.5 µM in the injection pipette) endophilin initially formed a striated pattern on the nanotube, marked by a brief (few seconds) beading instability (Fig. 1_C_, observed in 6 out of 31 experiments). The striation rapidly coarsened, leading to a growth of the scaffold from both bases of the tube. To some extent, this behavior is reminiscent of the way dynamin binds to membrane tubes. Dynamin binds in a striated pattern and affects the membrane force. In the case of dynamin, however, the membrane force changes only after the entire tube is covered with the protein (33, 34), contrary to endophilin, in which case a decrease in the force is seen immediately upon binding.
Role of Protein Subdomains in Scaffolding.
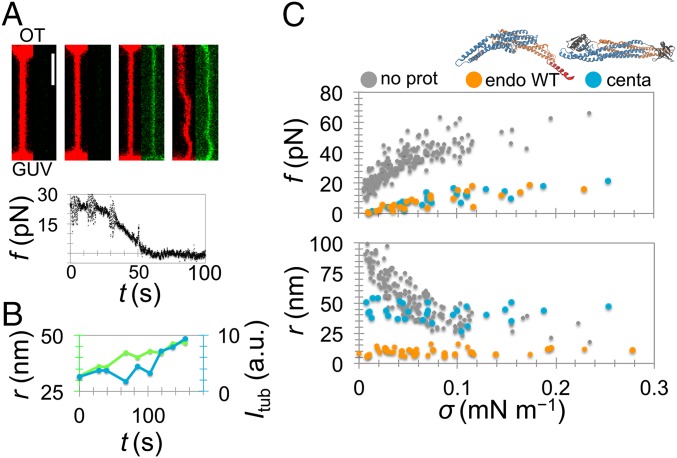
We then aimed to examine how changing the intrinsic curvature and the presence of amphipathic helices affect the scaffolding dynamics. β2 centaurin provides a good testing ground, because it is one of few BAR proteins without an N-terminal amphipathic helix (35). Additionally, the BAR domain of centaurin is much shallower than that of endophilin, as judged by their atomic models (SI Text and Fig. S4). Contrary to endophilin, centaurin bound homogeneously along the nanotube, with no detectable preference to the neck (Fig. 2_A_). Nevertheless, there was a reduction in the membrane force during binding, leading to a buckling instability at low tension (Fig. 2_A_). Importantly, binding of the protein changed the curvature of the tube, even though the aspiration pressure remained the same. Fig. 2_B_ shows an example where binding of β2 centaurin dilates a 30-nm tube by ∼20 nm. Furthermore, once the scaffold forms, either by centaurin or endophilin, the tube radius remains constant; its magnitude is characteristic of the protein, but independent of GUV tension (Fig. 2_C_). Namely, the tube scaffolded by centaurin is approximately four times wider than the one scaffolded by endophilin (42.5 nm compared with 10 nm, Table 1). This observation is in line with the difference in intrinsic curvatures of their BAR domains (Fig. S4).
Fig. 2.
Scaffolding by N-BAR versus BAR domains. (A) β2 centaurin BAR domain (amino acids 1–384) binds evenly along the tube (red, lipid and green, protein) and causes a decrease in tube-retraction force, f, just like endophilin. (Scale bar, 2 μm.) (B) Dilation of a narrow tube induced by a scaffold of β2 centaurin BAR domain (overlaid are fluorescence intensity of the protein on the tube, _I_tub, and the tube radius, r, deduced from lipid fluorescence). (C) The mechanics of the reference membrane (n = 45) and after the formation of a scaffold by endophilin A2 WT (endo WT, n = 7) and β2 centaurin (centa, n = 5). Tube force, f, measured from the optical trap; tube radius, r, measured from lipid fluorescence.
Table 1.
Radius of scaffolded tubes measured from lipid fluorescence
| Radius, r | endo WT | endo ΔH0 | endo mut | centa |
|---|---|---|---|---|
| nm (N) | 9.8 ± 2.8 (10) | 21.4 ± 11.6 (7) | 19.9 ± 3.0 (7) | 42.5 ± 7.0 (5) |
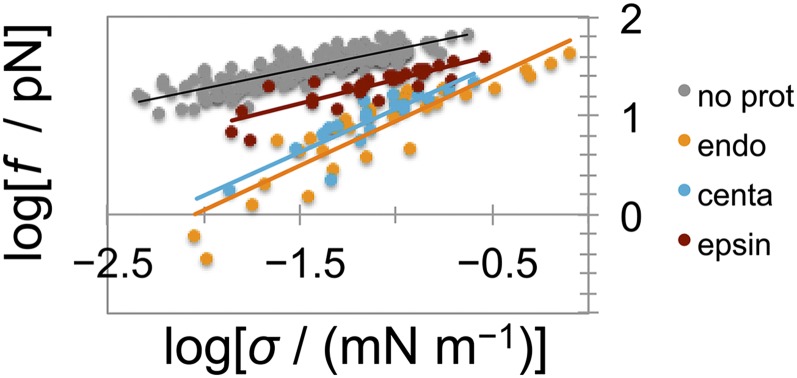
The formation of a scaffold by either endophilin or centaurin also drastically changes the mechanics of the membrane, evident from the systematic reduction in the equilibrium tube force for all tested membrane tensions (Fig. 2_C_). Based on previous analytical modeling, the force of a scaffolded tube—characterized by a constant radius—is expected to linearly depend on GUV tension, whereas a bare membrane is expected to have a square-root dependence (7, 25). Indeed, the membrane force of protein-covered tubes in experiments shown in Fig. 2_C_ displays a linear dependence on tension (Fig. S6), thus confirming the formation of a scaffold by a measurement independent of tube radius.
Fig. S6.
Scaling of force with membrane tension. Linear fit yields slopes for bare membrane (gray), 0.41 ± 0.02; for endophilin A2 scaffold (orange), 0.90 ± 0.08; for β2 centaurin scaffold (blue), 0.88 ± 0.12; and for epsin 1 (red), 0.49 ± 0.06.
These experiments demonstrate that both BAR domains that contain membrane-inserting amphipathic helices (endophilin) and those that do not (β2 centaurin) are capable of forming a rigid structure that controls the curvature of the membrane. They also show that proteins from the same family may bind to the membrane at different locations (we explore this point in the next section).
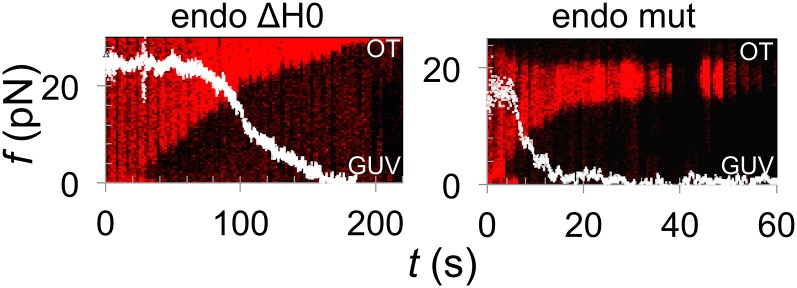
To further investigate the role of amphipathic helices versus the BAR domain in scaffolding, we constructed two endophilin mutants. In the first, we truncated the N-terminal amphipathic helix of the full-length endophilin A2 (endo ΔH0). In the second, we mutated one glutamate and one aspartate from the membrane-binding region of endophilin A2 N-BAR domain into lysines (E37K and D41K) (endo mut), which enhances the binding strength of the BAR domain to the membrane. Both variants constricted the tube starting from an interface (Fig. 3, red fluorescence) and decreased the force (Fig. 3, white plot) and tube radius (Table 1) in the same manner as the WT. This observation confirms that the N-terminal amphipathic helices are not necessary for the formation of the scaffold or, interestingly, for the preferential binding to the tube’s base in these experiments, although the scaffolding rate seems slower (Fig. 3).
Fig. 3.
Amphipathic helices do not determine the scaffold initiation site. Shown are force plots (white) overlaid on kymograms of lipid fluorescence of a membrane nanotube (red marker) during binding and scaffolding by endophilin mutants. As before, the formation of a scaffold is evident from tube constriction. (Left) Scaffolding by endophilin A2 with truncated N-terminal helices (endo ΔH0). (Right) Scaffolding by endophilin A2 N-BAR domain E37K, D41K (endo mut).
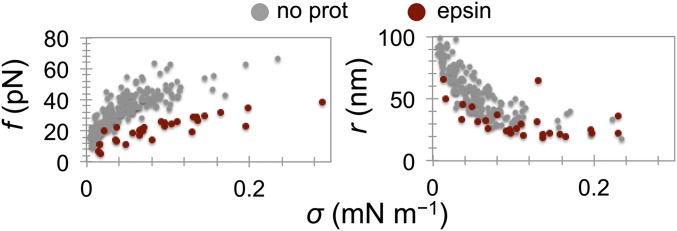
Finally, we tested the full-length epsin 1, another important endocytic protein that participates in the initial stages of clathrin-mediated endocytosis (36). Epsin does not contain a BAR domain; instead, it binds and bends the membrane via an amphipathic helix. There was a clear mechanical effect upon the injection of epsin 1, characterized by a systematic reduction in both the equilibrium tube force and the tube radius for a wide range of membrane tensions, indicating that the protein induces positive spontaneous curvature (7) (Fig. S7). Similarly to centaurin, the constriction did not start from the base; rather, it appeared homogenous along the tube length. Unlike endophilin and centaurin, the force never decreased to zero and so we never observed buckling. The square-root scaling of the force with membrane tension (Fig. S6) indicates that no scaffold forms, even at very high protein concentration (10-fold higher than minimal endo WT concentration that makes a scaffold). In summary, amphipathic helices alone may remodel the membrane, as in the case of epsin. However, the anisotropic BAR domain is critical for forming a rigid scaffold.
Fig. S7.
Epsin 1 alters membrane curvature and mechanics. Shown are the force and the tube radius after injecting epsin 1 at bulk concentrations of 2–5 µM (n = 5).
Pinning a Fluctuating Tube Determines the Protein’s Binding Site.
So far, we demonstrated that BAR proteins lacking amphipathic helices may form scaffolds just as N-BAR proteins; however, it is still unclear what determines the nucleation site of the protein. Our experiments cannot provide a general mechanism to answer this question and so we developed a mathematical model of BAR proteins interacting with a membrane tube. Several models have already been proposed for an equivalent system (7, 37), but those models did not capture the location of protein nucleation. We extend these models in two ways. First, we generalize the protein–membrane interactions by assuming that the proteins induce a local perturbation, expressed in terms of a tension or a pressure variation. Second, instead of taking periodic boundary conditions, we model a membrane tube pinned at its ends assuming that the radial displacement of the bilayer is strongly limited at the one end by the optical trap and at the other by the vesicle.
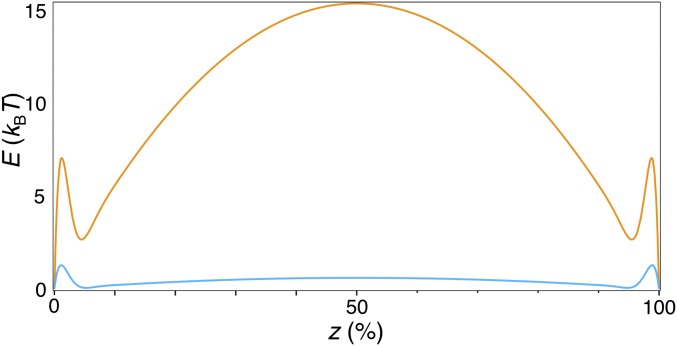
As we show in SI Text in detail, we decompose the free energy into the costs of (i) bending and (ii) stretching the membrane, supplemented by (iii) a term accounting for membrane–protein interactions and (iv) the energy associated with a point force keeping the membrane tubular (Eq. S14) (25, 37, 38). Solving the equation in the limit of low protein concentration, we obtain the mechanical strain energy variation (Eq. S17) induced by membrane–protein interactions, whose minima essentially indicate the binding sites of the protein. Importantly, the shape of this function strongly depends on the protein-induced local tension (or curvature) perturbation. When taking a local tension variation of Δσ=0.25%, the energy profile has a minimum at each of the tube’s ends separated by a very high energy barrier at the tube’s center (Fig. 4). Reducing the local perturbation fivefold to 0.05% lowers the barrier to <1 k_B_T and thermal fluctuations dominate (Fig. 4; see also SI Text and Fig. S8).
Fig. 4.
Strongly curving proteins nucleate at the base of a pinned and fluctuating tube. Mathematical model: strain energy variation profile, E, as a function of the axial position on the tube, z (in percentage of total length), plotted using Δσ = 0.25% (orange) and 0.05% (blue), κ = 50 k_B_T, L/r = 100.
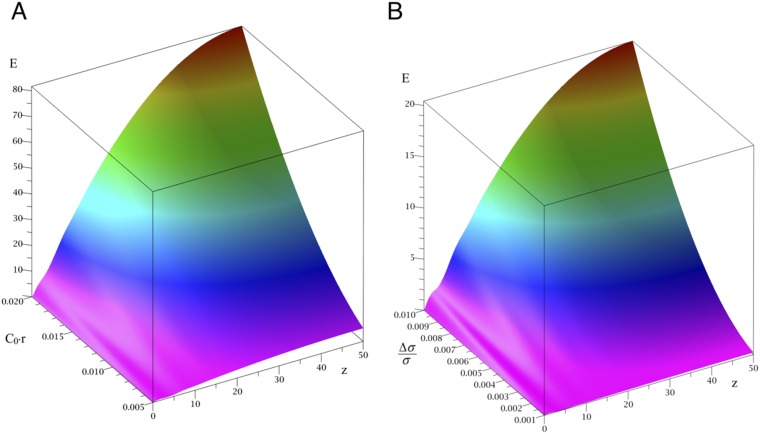
Fig. S8.
Mechanical strain energy profiles of protein-adsorbed pinned tubes. Plotted are mechanical strain energy, E, (in k_B_T units) versus the z coordinate (in L/100 units, where L is the tube length). (A) The effect of the spontaneous curvature, C_0, (in [r−1] units), for a tension perturbation of Δ_σ = 1%. (B) The effect of Δ_σ_, for the case of _C_0 = 0.45 _r_−1. Half-tube is shown, the profile being symmetric with respect to the tube’s center.
According to our model, proteins that significantly affect the local structure of the membrane preferentially bind to the necks of a pinned fluctuating tube. This conclusion is in excellent agreement with our observations. Endophilin A2, displaying a much higher intrinsic curvature of its N-BAR domain (Fig. S4_A_) and having four amphipathic helices (Fig. 2 and Table 1), is expected to very strongly locally perturb the bilayer, which is why it clearly nucleates at the tube–vesicle interface. β2 centaurin, however, displays a shallow curvature of the BAR domain (Fig. 2 and Table 1) and lacks amphipathic helices (Fig. S4_B_), which is why it binds homogenously along the tube. Both endophilin mutants were found to localize at the tube’s base. For the mutant that binds more strongly to the membrane this observation is not surprising in light of our theory. Surprisingly, however, endo ΔH0 is also found at the base despite lacking N-terminal helices. It seems that the shape and charge of endophilin’s BAR domain and the short insert helices present at the BAR-domain dimerization interface impose sufficient local bilayer perturbation to determine the protein’s localization.
Recall that our model is valid in the dilute limit, and therefore it cannot account for the emergence of the striated pattern that require a higher protein density. A previously developed model explaining FtsZ rings on tubes can be applied here instead (39). That model predicts that a higher protein concentration induces a uniformly unstable tube at a given tension, leading to a dynamic instability that promotes local protein condensates, separated by an energy barrier. Based on our experiments, this configuration is transient, because the scaffold readily covers the tube within a few seconds.
BAR Scaffold Is Not Densely Packed on the Tube.
In previous sections we discussed the mechanism of protein nucleation and the mechanical aspects of protein scaffolds. We now explore the potential molecular structure of scaffolds after they have formed. Previous EM images and CG simulations have revealed that at very high protein to lipid ratios N-BAR proteins amphiphysin and endophilin very densely assemble on liposomes, transforming 100- to 400-nm vesicles into tubules and tubular networks (9, 19, 40). Prior fluorescence microscopy experiments have shown that N-BARs form scaffolds when their density on the GUV exceeds ∼1,000 µm−2 (∼5% areal fraction if taking 50 nm2 as the area of the protein) (7, 10). We found a similar quantitative behavior for the BAR protein β2 centaurin. Namely, in our experiments, we measured an areal density of the protein dimer to be 3,600 ± 830 µm−2 on the GUV (18% coverage, n = 5; see SI Text for details on density measurements). As expected due to curvature sorting, the surface density on the tube was somewhat higher, measuring 7,400 ± 1,800 µm−2 (35% coverage). The surface density of dimeric endophilin A2 N-BAR domain on the tube was comparable, measuring 8,800 ± 5,300 µm−2 (43% coverage, n = 4), with a corresponding density on the GUV of 1,650 ± 750 µm−2 (8% coverage). Both protein measurements are comparable to 25% on the tube previously measured for amphiphysin (7).
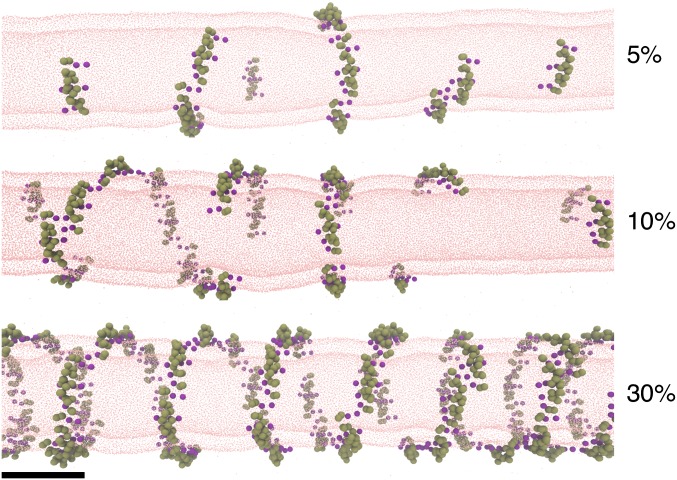
Our experiments therefore indicate that proteins do not need to be densely packed to form a scaffold as seen in EM experiments in vitro. To understand the structure of the scaffold at molecular resolution, we performed CG MD simulations of endophilin’s N-BAR domain on a 20-nm-wide lipid bilayer tube. We placed N-BARs at 5, 10, 30, and 40% surface coverage, starting either from a random or a tightly packed configuration, and carried out ∼30 million simulation time steps.
Regardless of the initial assembly of proteins and the protein density, we observed that N-BAR domains readily interacted with one another along their longitudinal axis, forming strings (Fig. 5). This arrangement resembles the membrane-mediated linear aggregation previously predicted for N-BAR proteins and, to a weaker degree, spherical particles (12–14, 41). Under confinement (on a flat or spherical surface), the proteins pack into a mesh (12); however, it seems that a tubular surface directs the proteins into a helix, with seven to eight N-BAR domains making a full helical turn (Fig. 5).
Fig. 5.
Simulation of N-BAR domains on nanotubes. Shown are final snapshots of CG MD simulations of membrane tubes coated with N-BAR proteins at the indicated protein surface densities. (Scale bar, 20 nm.)
We note that in CG MD simulations the helix contiguously wraps the tubule at 30–40% protein coverage, in excellent agreement with the experimentally measured scaffold density. Once attaining this density, the proteins cease to exchange neighbors and the helix becomes quasistatic (Fig. 5; also see SI Text and Fig. S9).
Fig. S9.
The formation of an N-BAR domain helix. (A) Structural properties of the helix from a CG simulation at 35% N-BAR density. (B) The distance between two representative N-BAR domains showing the convergence to the helical pitch distance. Taken from CG simulation at 35% density. (C) Dimerization kymogram showing the dimerization dynamics of two N-BAR domains as part of the helix at 35% density. M, monomer; D, dimer. (D) Polymerization kymogram, showing the dynamics of helix formation in a simulation at 12% density. Numbers on the y axis represent the number of N-BAR domains in the helix.
SI Methods
Reagents.
Total lipid brain extract (131101P), l-α-phosphatidylinositol-4,5-bisphosphate [PI(4,5)P2, 840046P], and 1,2-distearoyl-_sn_-glycero-3-phosphoethanolamine-_N_-[biotinyl(polyethyleneglycol)-2000] [DSPE-PEG(2000)-biotin] were purchased from Avanti Polar Lipids. BODIPY-TR-C5-ceramide, TR-1,2-dihexadecanoyl-_sn_-glycero-3-phosphatidylethanolamine (DHPE*), BODIPY-FL C5-ganglioside GM1 (GM1*), and BODIPY- FLC5-hexadecanoyl phosphatidylcholine (HPC*) were purchased from Molecular Probes. All reagents used to make buffers and β-casein from bovine milk (>99%) were purchased from Sigma-Aldrich. Polystyrene streptavidin-coated beads (diameter of 3.2 μm) were purchased from Bangs Laboratories.
Plasmids.
Rat endophilin A2 amino acids 1–247 was cloned into pGEX4T2 (GE Healthcare) and mutations were made to create a clone with a single cysteine residue available for labeling that did not interfere with membrane binding (C96A, C147A, and Q228C). Human β2 centaurin amino acids 1–384 was cloned in pGEX6p2 (GE Healthcare) and a cysteineless mutant was made (C10A, C42A, C53A, C156A, C321A, C316A, C329A, and C339A; a new cysteine was introduced in the N terminus).
Protein Purification.
GST-tagged proteins were expressed in BL21 DE3 bacteria at 18 °C overnight after the induction by 150 mM isopropyl β-d-1-thiogalactopyranoside, lysed in buffer (50 mM Hepes, pH 7.4, 500 mM NaCl, 2 mM DTT, and protease inhibitor mixture) under high pressure (high pressure homogenizer; Constant Systems). The cleared lysate was incubated with glutathione Sepharose (GE Healthcare) for 30 min at 4 °C. The GST tag was cleaved off using thrombin (Serva) or PreScission protease. The cleaved protein was passed over a Q Sepharose anion exchange column followed by a gel filtration column (S75 Sephadex; GE Healthcare). Endophilin A2 N-BAR domain and β2 centaurin were labeled with Alexa488 according to the manufacturer’s protocol (A10254; Life Technologies), concentrated, snap-frozen in liquid nitrogen, and stored at −80 °C. C-terminally strep-tagged endoA2 ΔH0 was purified as previously described (22). The full-length mouse endophilin A2 (N-BAR + SH3 domains) was a generous gift of Anne Schmidt, Institut Jacques Monod, Université Paris Diderot.
Preparation of GUVs.
GUVs were grown using electroformation on Pt wires in a solution of near-physiological ionic strength (51). First, a lipid mix was prepared in chloroform composed of ∼95% total brain extract and 5% (mol/mol) PI(4,5)P2 (molar ratios, molar mass of the extract approximated at 800 g⋅mol−1) and it was kept in a glass vial under an Ar atmosphere. The lipid mix was deposited onto a pair of Pt wires, in drops separated by 0.5 cm (total volume of ∼4 µL). The wires were dried under vacuum for 30–60 min then hydrated in a solution of 70 mM NaCl, 100 mM sucrose, and 10 mM Tris, at pH 7.4. A sine alternating current was then applied through the Pt wires at 500 Hz and 280 mV. The GUVs were grown overnight in a refrigerator (4 °C). Although the composition of the solution inside GUVs could in principle be different, deviations from these optimized conditions typically resulted in low GUV yield or too many small, multilamellar, and tense vesicles. In addition, these conditions produce GUVs that gain excess surface area within 15 min of being collected, ideal for micropipette-aspiration experiments. Importantly, we disconnected the wires just before each experiment, collected GUVs directly from the wires using a pipette (∼10 µL of final solution per droplet of the lipid mix), transferred them on ice, and used them as soon as possible. We did not use GUVs for more than 4 h.
Tube Pulling.
The experiments were carried out on a Nikon TE2000 inverted microscope equipped with an eC1 confocal system (Nikon). There were two laser lines operating at λ = 488 nm and λ = 543 nm. The optical path was supplemented with optical tweezers, induced by a 5-W ytterbium fiber continuous-wave laser emitting infrared light (λ > 1,070 nm; IPG GmbH). We used a water-immersion objective (60× magnification and numerical aperture 1.27).
The experimental chamber was constructed by attaching two coverslips onto a custom-built metal frame so that the two coverslips were separated by ∼2 mm. The experimental chamber and the aspiration pipette were filled with a 5 g⋅L−1 solution of β-casein (dissolved in 100 mM NaCl and 10 mM Tris, pH 7.4) so as to minimize the adhesion of lipids to the glass surface. The tip of the aspiration pipette connected to a water tank was brought inside the experimental chamber with an x-y-z micromanipulator. In addition to the micromanipulator, the horizontal position of the aspiration pipette was controlled with a piezoelectric actuator (Physik Instrumente).
Casein was incubated for 30 min. The chamber was then rinsed several times with the experimental buffer (100 mM NaCl and 40 mM glucose, buffered with Tris to pH 7.4). Importantly, the ionic strength of solutions used to grow GUVs (solution inside GUVs) and for tube-pulling experiments (solution outside GUVs) was confirmed to be within 10 mOsm using an osmometer (Loser) to avoid osmotic shock. Then, we filled the chamber with the experimental buffer and added a fractionate amount of polystyrene beads into the chamber. Another pipette was filled with the solution of a protein diluted with the experimental buffer containing ∼20 mM more glucose to offset for evaporation during the waiting period. Concentrations of proteins inside the pipette (per dimer) were the following: 0.5–2.5 µM endophilin A2, 0.5–2.5 µM endophilin A2 E37K, D41K, 3.5 µM endophilin A2 ΔH0, 0.5–3.5 β2-centaurin, and 2–5 µM epsin 1. Only the tip of the injection pipette was filled by suction, then the back of the pipette was filled with mineral oil, leaving no air inside the pipette. The vesicles were left to deflate for 10–30 min, after which we sealed the chamber with mineral oil to prevent evaporation.
GUVs with enough excess area (i.e., those with visible undulations) were aspired in a micropipette tip (24, 52). The aspiration (hydrostatic) pressure, Δp, sets the membrane tension according to σ=0.5Δprpip/(1−rpip/rves), where rpip and rves are, respectively, the radii of the pipette and of the GUV. Then, we gently tethered the GUV to a bead in the optical trap and pulled back, forming a tubular membrane between the GUV and the bead. Subsequently, we injected the desired solution with another pipette in the close proximity of the tether at a pressure of 1–2 Pa. During the experiment, we would set the aspiration pressure, record the bright-field microscopy image at 30 frames per s, and take several images with the confocal microscope. After several minutes, we would change the aspiration pressure and repeat the procedure. Typically, we would do a set of measurements before and another set after injection to see the effects on the same vesicle. Of note, the direction of aspiration pressure (increase or decrease) does not change the force at a given tension (Fig. S2).
We measured the force by tracking the movement of the trapped bead, according to Hooke’s law: f=kOT(a−a0), where kOT is the stiffness of the optical trap, calibrated using the viscous drag method, and a and a0 are, respectively, the average and the equilibrium positions the bead. Radius of the tube can be deduced from the force as R=f/4πσ (see SI Text, Physical Properties of the Membrane for more details); however, it can also be measured from the intensity of fluorescent lipids in the tube. The mean intensity of the tube, Itub, is proportional to its circumference, implicitly radius; it can be divided by the lipid fluorescence intensity in the vesicle, Ives, to normalize for the variations in fluorescent lipid incorporation between experiments. Therefore, r=KtubItub/Ives, where Ktub is a calibration constant, previously determined to be Ktub= 200 ± 50 nm from force measurements using the same lipid fluorescence reporter (7).
CG MD Simulations.
We used a previously developed solvent-free three-site CG lipid model (55). One site represents the hydrophilic head group, whereas the other two represent the hydrophobic tails of a lipid. A previously developed model of an N-BAR domain of endophilin A1 was used. The model comprises 26 CG sites, where the intraprotein interactions were modeled as harmonic bonds by using the elastic network model (9), whereas protein–protein and protein–lipid interactions were modeled with a Lennard-Jones potential as described previously (12).
We simulated lipid bilayer tubes coated with N-BAR domains at 5, 10, 30, and 40% surface coverage. A tube 150 nm in length and 20 nm in diameter was enclosed inside a simulation box in a way that it interacts with its periodic images in the z directions (making it virtually infinite in length), leaving at least 50 nm of space in the x and y directions.
To equilibrate the structure, first we ran energy minimization then several MD simulations with time steps increasing from 1 fs to 10 fs (total of ∼600,000 time steps). We ran the simulations at constant NVT conditions (V being the volume of the box, N being the number of molecules in the box, and T the temperature of the thermostat, set at 300 K). Next, we placed a desired density of CG N-BAR domains on the surface of the tube, either randomly or in a closely packed arrangement. We repeated the equilibration as above. Then, we carried out production run simulations for ∼30 million time steps at a time step of 12 fs for all simulation systems using the MD suite LAMMPS (56). It is to be noted that the simulation time inferred from CG simulations does not exactly correspond to the actual simulated time.
Discussion
Two related curvature-generating proteins can initiate a scaffold at different membrane locations, as shown by our in vitro reconstituted system. Namely, an N-BAR protein endophilin nucleates at the tube’s ends, whereas a BAR protein centaurin binds evenly along it. Our mathematical modeling predicts that specific binding to the saddle-shaped neck of a pinned and fluctuating membrane tube is a consequence of strong local membrane perturbations. An important conclusion from these observations is that the nature of local protein–membrane interactions can affect the specific initial localization of proteins on curved membranes and, thus, the dynamics of their assembly on membrane-remodeling sites.
Although the complexity of multiprotein interactions may divert the nucleation preference of BAR proteins in a cell, our findings seem to agree very well with previous in vivo studies of endocytosis. Immunoelectron microscopy of endophilin on clathrin-coated pits in cells at endogenous protein concentrations showed that endophilin indeed sits at the base of the clathrin coat (42). In the same study, in cells treated with a nonhydrolysable GTP, which form long dynamin-covered tubes, endophilin was again only found at the base of the coat (42). By contrast, dynamin was found all along the tubule’s length.
Endophilin interacts with other proteins in a dynamic way. Namely, the tubulation efficiency and the amount of dynamin recruited to GUVs or lipid tubules are significantly increased by endophilin, and vice versa (42, 43). Furthermore, acutely perturbing endophilin using antibodies against the SH3 or the BAR domain stalled the formation of clathrin-coated pits before the sculpting of a narrow neck and the saddle (44, 45). Hence, endophilin could potentially play important roles in directing other endocytic proteins to their binding site.
Concerning protein’s subdomains, the BAR domain seems crucial for the formation of a rigid scaffold. As previously demonstrated on a flat membrane, local membrane deformations mediate the interactions among BAR proteins and induce their assembly. The anisotropic shape of the BAR domain likely further facilitates an ordered packing and the formation of a scaffold. Therefore, a BAR domain is indeed a scaffolding domain, although not because a single protein imprints its shape on the membrane, but owing to a collective effect imposed by an ordered membrane-mediated helical assembly. Moreover, amphipathic helices seem dispensable in scaffolding; however, their role is still important in facilitating protein recruitment to the membrane (22) and in increasing the membrane’s spontaneous curvature (Table 1). They may also have a role at the molecular level to help properly orient the BAR domains into a rigid scaffold, evidenced by the wide distribution of tubular radii when they are truncated (Table 1) (22), agreeing with previous work (9).
Importantly, our results show that a scaffold can form at much lower surface densities than full packing. Dense protein packing would be problematic for endocytosis. According to previous simulations, the shape of a basic unit of a BAR-domain lattice on the membrane affects the radius of the scaffold (18). Therefore, the radius of the tubule scaffolded by the same protein would be variable, depending on the way it formed the lattice, which seems unfavorable for endocytosis and trafficking, which require a tight curvature control. Indeed, tubule radii from different in vitro studies were infrequently different for the same protein. For example, tubule radii formed and scaffolded by amphiphysin 1 in vitro (measured between the membrane midplanes) were found to be 21 nm (35) and ∼11 nm (46), both based on EM imaging, compared with 7 nm measured by fluorescence microscopy (7). Based on our combined experimental and simulation data, under protein concentrations much lower than those used in EM imaging in vitro, BAR proteins do not build lattices on preformed tubes. Instead, they only cover 30–45% of the surface (depending on the protein), forming a stable and a rigid scaffold with constant curvature, bearing resemblance to in vivo EM images in which membrane tubules were created in the cell by endogenous protein concentrations (42, 47). In turn, this assembly provides structural integrity for endocytosis and leaves sufficient membrane area for the binding of accessory proteins crucial in the process (42, 46, 48).
Based on our work, we can propose different biologically relevant purposes for the N-BAR domain scaffolds. First, in endocytosis, they constrict the membrane tube between the endocytic vesicle and the underlying membrane, thus reducing the energy barrier for scission by dynamin (33) or by elongation forces (22). Second, highly curving proteins such as endophilin are specifically recruited to the neck, and so in clathrin-dependent endocytosis, where endophilin recruits dynamin to the tube (43), the scission site will be highly localized to the base of the coat. Third, scaffolds provide a powerful control of membrane curvature that may be used in forming complex cellular architectures, such as in the formation of T-tubules or the maintenance of mitochondrial shape, which require N-BAR proteins amphiphysin 2 (49) and endophilin B1 (50), respectively. The subtle differences in structures of these proteins give rise to a complexity in intracellular architectures and the highly dynamic behavior of the membrane. These differences are also likely the key way of modulating the function and localization of BAR proteins. We also expect that in the near future the higher-order organization of BAR proteins will be shown to be crucial in additional important membrane-remodeling phenomena.
Methods
Pulling Nanotubes and Making Protein Scaffolds.
GUVs [95% total lipid brain extract (26), 5% (mol/mol) PI(4,5)P2, supplemented with 0.1% di-stearoyl phosphatidyl ethanolamine-PEG(2000)-biotin and 1% BODIPY TR ceramide] were prepared by electroformation on Pt wires overnight at 4 °C in a salt-containing buffer (51). To pull a tube, the GUV was aspirated in a micropipette, brought in contact with a streptavidin-coated optically trapped bead, then gently pulled away. Proteins were injected near the tube with another micropipette. The aspiration pressure sets the membrane tension and the tube radius, r, in the absence of proteins, as r=κ/2σ, where κ is membrane stiffness and σ is membrane tension (7, 24, 52–54). The tube force, f, was measured by videomicroscopy as f=kOT(a−a0), where kOT is the trap stiffness and a and a0 are the current and the equilibrium bead positions, respectively. The r (in the presence or absence of proteins) was measured from lipid fluorescence as r=KtubItub/Ives, where Itub and Ives are the fluorescence intensities of lipids in the tube and in the GUV, respectively, and Ktub = 200 ± 50 nm is a previously measured calibration constant (7, 32).
CG MD Simulations.
We used a solvent-free three-site CG lipid model (55) and a 26-site elastic network model of an N-BAR domain dimer of endophilin A1 (9) with protein-membrane interactions modeled using a Lennard-Jones potential as described previously (12). We simulated N-BARs on a lipid bilayer tube (150 nm in length and 20 nm in diameter interacting with its periodic images in the tube direction) at 5, 10, 30, and 40% surface coverage. The simulations were carried at a constant number of molecules, box volume, and temperature for ∼30 million time steps at a time step of 12 fs using LAMMPS (56).
SI Text
Measuring the Surface Density of Proteins.
To measure the density of proteins (endophilin A2 and β2 centaurin) bound to the membrane, we applied a previously developed quantification protocol (7). The method is based on calibrating the density of the protein by relating its fluorescent intensity to the intensity of another fluorescent molecule for which we can easily quantify the amount. As the reference fluorophore we used a fluorescent lipid HPC*. We can write the surface density of the fluorescent protein on the GUV, φprot,ves, in terms of the density of HPC*, φHPC∗,ves, as
| φprot,ves=φHPC∗,vesIprot,b/IHPC∗,b. | [S1] |
|---|
We correct the surface density by the ratio of intensities of the Alexa488-conjugated protein and HPC* in bulk, Iprot,b/IHPC∗,b considering that the two fluorophores do not necessarily emit the same intensity at the same concentration. Hence, first we determined the ratio of fluorescence intensities between Alexa488 (bound to a protein) and HPC* in bulk (dissolved in mineral oil), yielding a ratio close to unity, Iprot,b/IHPC∗,b= 0.91 ± 0.05. Next, we measured the fluorescence intensity of GUVs composed of egg-PC complemented with HPC* at mole fractions χ = 0.01–1%. We assume that the incorporation of the fluorescent lipid into the GUV is stoichiometric. If we take the area per lipid 0.7 nm2, the number of HPC* per square micrometer per leaflet is 1.43 million multiplied by χ. As expected, fluorescence intensity linearly depended on the HPC* concentration in bulk and in the GUV (Fig. S1), that is,
| φHPC∗,ves=AcalIHPC∗,ves. | [S2] |
|---|
The slope of intensity with respect to HPC* concentration, Acal, depends on the selected detector sensitivity (i.e., gain) and the applied neutral density filter and needs to be calculated for each microscope setup as the inverse of the slope of the plot in Fig. S1_B_. We determined the number of Alexa488 fluorophores per molecule of the protein, _n_f, by measuring the absorbance using a NanoDrop (Thermo Scientific), yielding in our case 1.3 per monomeric β2 centaurin and 1.5 per monomeric endophilin A2. Finally, the surface density of a dimeric BAR/_N_-BAR was calculated as
| φBAR,ves=AcalIBAR,ves0.91×2×nf. | [S3] |
|---|
We calculated the surface density of proteins on the tube by multiplying the density on the GUV by the sorting ratio, S,
S is calculated as fluorescence intensity ratio of proteins on the tube and the vesicle normalized by the same lipid fluorescence intensity ratio, or
| S=IBAR,tub/IBAR,vesIlip,tub/Ilip,ves. | [S5] |
|---|
Physical Properties of the Membrane.
Mechanics of the membrane in the absence of proteins.
We examined the viability of GUVs composed of the total brain extract supplemented with 5% (mol/mol) PI(4,5)P2. First, we tested the mechanical properties of the membrane by carrying out tube-pulling experiments in the experimental buffer and in the absence of any curvature-generating molecules. Fig. S1 shows an experiment on a GUV where we initially increased membrane tension in discrete steps then repeated the measurements by stepwise decreasing membrane tension, all while injecting a (non-curvature-active) buffer solution. As expected, with increased membrane tension, the membrane force increased while the radius of the tube decreased (Fig. S2). We also confirmed that the values of force and radius are not appreciably affected by the direction of the change of membrane tension (Fig. S2, black versus gray dots). This measurement implies that the bilayer is fluid, because any change in tension prompts the lipids to flow between the vesicle and the tube. Otherwise, the force and the radius would remain unaltered.
To quantify our data, we minimize the Helfrich Hamiltonian (53) with respect to tube length and radius at a given membrane tension, yielding
where f is membrane force (precisely, the tube-retraction force), r tube radius, _r_0 radius of spontaneous curvature, σ is membrane tension, and κ is bending stiffness (24, 25). The equations reveal that the curvature (i.e., inverse radius) and the membrane force of the tube scale as the square root of membrane tension.
Fitting the model to our data gives κ. Considering that we measured the radius from the fluorescence intensity and not from the force, we have two independent measurements of κ (Fig. S2). Fitting the force equation (Eq. S6) to our data yields κ = 46.1 ± 4.5 k_B_T (mean ± SD) (n = 45; n is the number of experiments), whereas fitting to the tube radius measurements yields κ = 57.4 ± 3.4 k_B_T (n = 36). In both cases, _k_B is the Boltzmann constant and T the thermodynamic temperature (300 K). Although these values are higher than typical values of synthetic phosphatidyl lipid vesicles (∼20 k_B_T), they are comparable to the rigidity of the red blood cell (43 k_B_T) (54). Moreover, it is not surprising to find a higher κ, considering that the mixture contains sphingomyelins and lipids with chains of varying lengths and saturation (26, 27).
According to Eqs. S6 and S7, in the absence of spontaneous curvature the offset of the force and the radius should be zero. Fitting yields offsets of (6.8 ± 1.7) × 10−3 nm−1 (Eq. S6) and (3.9 ± 4.1) × 10−3 nm−1 (Eq. S7), corresponding to spontaneous radii of curvature of 150 nm and 250 nm, respectively. A positive offset in the force indicates a negative radius of spontaneous curvature. We note that a positive offset in the force has been reported for charged GUVs (31, 32), attributed to either a difference in the ionic strengths of solutions inside the GUV and the experimental buffer or to the interaction of Na+ with the bilayer (31). However, considering the size of a BAR domain (∼12 nm), we can neglect the spontaneous curvature of the membrane relatively to that of the protein.
Phase behavior of the bare membrane.
Considering that the total brain extract contains many lipids of varying chain lengths (26), it is possible that our GUVs could undergo phase separation. We tested the phase behavior of our model membrane by using fluorescent lipids known to partition into different phases. In particular, we doped the membrane with GM1* (at 1% molar fraction), a lipid equally distributed between the liquid ordered (lo) and the liquid disordered (ld) phases, and DHPE* (at 0.5% molar fraction), a lipid that strongly favors the ld phase. Of note, the same lipid dyes were previously used in studying the curvature sorting of lipids (28).
Using confocal microscopy, we observed a homogenous distribution of the two fluorescent lipids in all imaged GUVs (n = 16) (Fig. S3_A_). It seems that the membrane composed of the total lipid brain extract and 5% PIP2 does not phase-separate.
Next, we tested whether lipids get sorted by membrane curvature. We measured the fluorescence intensity of the two dyes in the tube, relative to that in the GUV, at different membrane tensions (implicitly curvatures). The relative ratio of the two dyes is the lipid sorting ratio, _s_lip:
| slip=1PfItubDHPE∗/ItubGM1∗IvesDHPE∗/IvesGM1∗, | [S8] |
|---|
where Itub and Ives are the fluorescence intensities of the individual dyes (as indicated in the superscript) in the tube and vesicle, respectively. Pf is the polarization factor, which takes into account the polarization of the excitation light and is measured as the relative ratio of intensities of one dye over the other in the absence of sorting. Pf depends on lipid composition, and for the total brain extract it measures 2.1 ± 0.3 (mean ± SD, n = 4). This value is consistent with previous measurements for sphingomyelin-containing ternary composition GUVs (28). As shown in Fig. S3_B_, neither labeled lipid gets enriched in the tube with increased curvature. According to a previous study, the absence of lipid sorting indicates that the membrane is not close to a demixing point (28). In conclusion, our GUVs are viable model systems of a fluid membrane, based on the observed mechanical and phase properties.
Visualizing Protein Structures.
To gain a better understanding of the molecular structure of proteins used in this study, we used Swiss-Model (https://swissmodel.expasy.org) to construct 3D models of the proteins based on the X-ray structures of their closest homologs. To model the N-BAR domain of rat endophilin A2, we used rat endophilin A1 as the homolog [Protein Data Bank (PDB) ID code 2C0B], whereas for the modeling of human β2 centaurin (BAR + PH domains) we used the structure of β1 centaurin as the homolog (PDB ID code 4NSW). Endophilins belong to N-BAR proteins, whereas centaurins belong to the classical BAR domain family. A noteworthy difference between the two proteins, besides lacking the N-terminal amphipathic helices, is that the BAR domain of β2 centaurin displays a much shallower curvature than the BAR domain of endophilin A2 (Fig. S4).
Additional Scaffolding Statistics.
The results shown in Fig. 2_C_ represent data in which the tube was constricted along the entire length and displayed a monotonous dependence of the force with membrane tension. As reported in Results, the scaffold changes scaling laws of the membrane, which can be seen from the linear fit of the log-log data of the force (Fig. S6). We note that these results are equivalent with the so-called high-density regime reported for amphiphysin (7). To specify, there were a total of 59 experiments for endophilin and 6 cases of centaurin in which we observed the scaffold formation, evidenced by the clear change in the tube radius. We systematically measured F versus σ in 26 cases for endophilin and 6 cases for centaurin. Out of those cases, seven cases of endophilin and five cases of centaurin displayed the dependence as in Fig. 2.
In the remaining cases, the scaffold partially covered the tube, characterized by a constant nonzero force at any tension (13 cases of endophilin) or covered it fully, characterized by a constant zero force at any tension (six cases of endophilin and one case of centaurin). Both case types are likely a consequence of kinetic trapping due to rapid squeezing of the water and the free membrane upon the initial tube constriction. Interestingly, such kinetic trapping has been predicted in the theoretical work explaining dynamin binding (39). In fact, we often observed that the membrane tube following the wave of the growing scaffold becomes significantly deformed (as seen in Fig. 1_A_), which can trap the protein growth to fully cover the tube. At present, we do not explore these kinetically dominated intermediate regimes because they do not add to or limit the conclusions that we draw in this paper. More importantly, in the cases where the force monotonously rose with membrane tension, it is reasonable to assume that the system has reached thermodynamic equilibrium, because the radius and the force remained constant after a few minutes of measurements.
Mathematical Model of BAR Proteins Binding to Pinned Membrane Tubes Subjected to Thermal Fluctuations.
We propose a mathematical model of BAR proteins interacting with a tubular lipid membrane. Proteins are considered to act at the molecular level, such that their binding alters the local adhesive interaction characteristics, modeled via a local tension variation Δ_σ_ and a local curvature variation Δ_c_. In addition, the adsorption of a sufficiently high number of proteins increases the average spontaneous curvature c0. We note that separating the contributions of the BAR domain versus the amphipathic helices to the three variables is far from trivial, so we consider the two modules as acting in concert.
Contrary to the majority of previous models where periodic boundary conditions were assumed, we take the tube to be pinned at its ends (38). We justify this condition because the radial displacement of lipids is strongly limited at both ends, on the one by the optical trap and on the other by the vesicle. As we show below, pinned boundary conditions are the key ingredient in demonstrating the specificity to the base of the tube by proteins that strongly curve the membrane.
Extending previous work (25, 37, 38) the free energy of the membrane can be written as
| ℱ=κ2∫(1r1+1r2−2c0)2dA+σ∫dA−Δp∫dV−fL, | [S9] |
|---|
where κ is the bending rigidity, r1 and r2 are the membrane’s principal radii of curvature, σ is the surface tension, L is the tube length, and f is the longitudinal stretching force applied to the tube; dV and dA are the vesicle volume and surface differentials, respectively.
The reference state of the tube is a cylinder of radius r, such that r/L≪1. In the limit of low protein concentrations (i.e., in the course of initial protein binding), this limit is negligibly perturbed. Minimizing the free energy in Eq. S9 with respect to r and L, and neglecting the pressure difference, we obtain two generalized Laplace equations:
We introduce a dimensionless parameter α=fr/(πκ), where α=2 corresponds to a system with vanishing spontaneous curvature.
The radial displacement field of a tube subjected to thermal fluctuations, ur, which depends on the azimuthal angle ϕ and on the longitudinal axis coordinate z in the cylindrical coordinate system, can be cast in the following form:
| ur(ϕ,z)=∑n=−∞∞∑m=1∞An,mei(nϕ)sin(kmz), | [S12] |
|---|
where km=πm/L, m=1,2,…,∞, and An,m are the amplitudes of the fluctuation modes. It is sufficient to consider the case of small fluctuations and limit the free energy expansion by the second-order terms in An,m. In the vicinity of equilibrium the free energy then obtains the following form:
| ℱ=12πLκr3∑n=−∞∞∑m=1∞Mn,mAn,mAn,m∗+κπ2αL∑m=1∞A0,m(1−(−1)m), | [S13] |
|---|
where Mn,m=(r2km2+n2−1)2+αr2km2, which depends on a single dimensionless effective parameter α.
As seen in Results, N-BAR proteins reduce the tube force and thus the parameter α. As illustration, in the case of a vanishing force applied to a pinned tube, and taking L/r=100 and κ=12 k_B_T, the root-mean-square fluctuation amplitude is about 2,500% of r. Clearly, the fluctuations become extremely important.
The local energy variation of the lipid–solvent interface together with the protein–lipid interactions lead to a local perturbation of the membrane near the protein’s binding site. This perturbation is equivalent to the action of a local delta-like pressure Π applied at the protein adsorption site. Its amplitude depends on both Δσ and Δc and, in a first approximation, can be estimated as Δ(σc)=cΔσ+σΔc, where σ and c are the average surface tension and the average curvature of the tube, respectively. The energy of the tube interacting with the proteins adhering to an initially bare membrane thus obtains the following form:
| ℱ=κ2∫(1r1+1r2−2c0)2dA+σ∫dA−∫ur(ϕ,z)δΠ(ϕ,z)dA−fL. | [S14] |
|---|
The interaction between the proteins and the vesicle is ignored in the limit of low protein concentration. The delta-like pressure perturbation can be represented as follows:
| δΠ(ϕ,z)=Δ(σc)∑n=−∞∞∑m=1∞Πn,me−i(nϕ)sin(kmz). | [S15] |
|---|
The amplitudes Πn,m=∑Ne−inϕNsin(kmzN), where N is the protein’s number, explicitly depend on the positions zN where the protein binds to the tube. Now, we determine the radial displacement field arising on the tube in response to a perturbation. Without losing generality and for the sake of simplicity we study in detail the case where the local protein–tube interaction mainly changes Δσ with negligible variation in Δc. The opposite case is straightforward; however, the mathematical description of the general case involving both Δσ and Δc is cumbersome and beyond the scope of this work. Thus, we take Δ(σc)≈cΔσ=Δσ/r.
From the classical theory of elasticity, we obtain the radial displacement field resulting from a perturbation of the tube:
| ur(ϕ,z)=r3Δσκ∑n=−∞∞∑m=1∞Πn,me−inϕsin(kmz)Mn,m. | [S16] |
|---|
By substituting the amplitudes of ur harmonics in the free energy expansion in Eq. S14, we get the mechanical strain energy variation of the membrane induced by the local adhesion of one protein to an initially bare membrane:
| E=12πLΔσ2r3κ∑n=−∞∞∑m=1∞sin2(kmz1)Mn,m+π2Δσr3αL∑m=1∞(1−(−1)m)sin(kmz1)mM0,m. | [S17] |
|---|
By iterating the same procedure, we can obtain similar expressions for the strain energy variation upon the adhesion of several proteins. This energy variation is clearly a function of the localization of perturbation induced by the protein. It consists of two terms; the first term—quadratic in mode amplitudes—is associated mainly with the thermal fluctuations of the tube, whereas the second term is associated with the shape of the tube. Plotting the full strain energy variation yields the plot in Fig. 4, which clearly shows that protein strongly favors the ends of a pinned tubular membrane. The corresponding energy minima at the very ends and in their vicinity are separated by a high-energy barrier with a maximum in the middle of the tube.
This strain energy variation has a minimum larger than k_B_T only for proteins that cause a sufficiently high Δσ variation. Reducing Δσ from 0.25 to 0.05% reduces the free energy barrier in the center of the tube to 1 k_B_T (Fig. 4). In that case, the strain energy profile is obfuscated by thermal fluctuations and as a consequence such proteins do not show a preference to where they bind.
Nonzero average spontaneous curvature also influences the relative values of the strain energy in its maxima and minima, although the energy profile does not qualitatively change. The plot in Fig. S8 illustrates how the increase in spontaneous curvature results in the increase of the strain energy difference between protein binding to the center of the tube versus binding near its ends. Analogously, to estimate the influence of the local adhesive interaction, we fixed the spontaneous curvature and followed how the strain energy variation profile changes as a function of Δσ. Apparently, an increase in Δσ leads to a significant increase in the aforementioned strain energy difference (Fig. S8_B_).
In summary, our analytical model is in excellent agreement with our experimental findings on the preferred localization of endophilin to the tube’s ends from which it initiates scaffolding. Apparently, two key ingredients were missing in previous models (7, 25, 37): (i) a fluctuating tube pinned at its ends and (ii) a sufficiently strong local perturbation, which in our case was modeled as a change in local surface tension or local curvature. The latter component explains why β-centaurin—a protein inducing a much shallower spontaneous curvature and lacking amphipathic helices—does not bind from the neck.
Molecular Structure of Protein Scaffolds from CG MD Simulations.
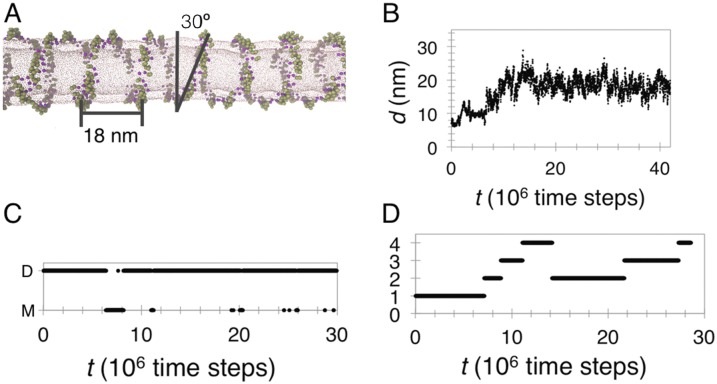
As described in Results, CG MD simulations show that N-BARs form a helical arrangement on a tubular membrane. Here, we detail additional measurements and further discuss the CG MD simulations. In the helix, we measured an angle of 30° between the helical turn and the tube axis, seven to eight N-BAR domains in a full helical turn, and a helical pitch of ∼18 nm (Fig. S9).
Fig. S9_B_ plots a minimum distance between two N-BAR domains from neighboring helical turns, showing that the proteins gradually transform from a close assembly into a helix at ∼15 million time steps, after which the helical pitch remains constant. The dimerization kymogram in Fig. S9_C_ demonstrates that proteins do not exchange neighbors over the course of a simulation once a contiguous helix has formed.
Interestingly, at low densities, the proteins still form helical assemblies with the same ∼30° angle. An alternative assembly would be a contiguous helix with a greater angle; however, we never observed such structure. Instead, the proteins locally assemble, although at densities <30% they are more dynamic, locally breaking and reforming the helices (see the kymogram in Fig. S9_D_).
It is to be noted that in our study we start with a radius of the tube that has little mismatch with the scaffold radius (i.e., ∼10 nm), so as to overcome computationally intractable timescales of the initial tube constriction. Therefore, we simulated a steady-state configuration of the proteins on tubular membranes. A recent computational study simulated BAR proteins as rods of adjustable intrinsic curvature embedded in a quasicontinuum membrane and demonstrated that highly curved rods undergo a phase separation marked by a condensation of the protein and a tube constriction (57). If starting from a vesicle, rods aggregate, leading to disk-like and tubular deformations (57, 58). The phase-separated state where proteins locally aggregate on the tube could be a metastable state after which the proteins equilibrate, leading to much less dense structure that we observe and believe are in fact the molecular structures of BAR-domain scaffolds on membrane tubes.
Supplementary Material
Supplementary File
Acknowledgments
We thank A. Callan-Jones for insightful discussions. This work was supported by National Institutes of Health Grant R01-GM063796 (to M.S. and G.A.V.), National Science Foundation Extreme Science and Engineering Discovery Environment Computational Resources (XSEDE) Grant TG-MCA94P017 (supercomputer Stampede), Agence Nationale pour la Recherche Grants ANR-11BSV201403 (to P.B.) and ANR-09BLAN283 (to H.-F.R. and L.J.), European Research Council Advanced Grant 340485 (to L.J.), and Medical Research Council Grant U105178795 (to E.E. and H.T.M.). M.S. was funded in part by a Chateaubriand Fellowship, a France and Chicago Collaborating in the Sciences grant, and the University Paris Diderot. The P.B. group belongs to the CNRS consortium CellTiss, the P.B. and L.J. groups belong to the LabEx CelTisPhyBio (ANR-11-LABX0038) and Paris Sciences et Lettres (ANR-10-IDEX-0001-02), and the V.L. group belongs to the LabEx NUMEV.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.H.H. is a Guest Editor invited by the Editorial Board.
References
- 1.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438(7068):590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 2.Phillips R, Ursell T, Wiggins P, Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459(7245):379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mim C, Unger VM. Membrane curvature and its generation by BAR proteins. Trends Biochem Sci. 2012;37(12):526–533. doi: 10.1016/j.tibs.2012.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Qualmann B, Koch D, Kessels MM. Let’s go bananas: Revisiting the endocytic BAR code. EMBO J. 2011;30(17):3501–3515. doi: 10.1038/emboj.2011.266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Suetsugu S, Toyooka K, Senju Y. Subcellular membrane curvature mediated by the BAR domain superfamily proteins. Semin Cell Dev Biol. 2010;21(4):340–349. doi: 10.1016/j.semcdb.2009.12.002. [DOI] [PubMed] [Google Scholar]
- 6.Rao Y, Haucke V. Membrane shaping by the Bin/amphiphysin/Rvs (BAR) domain protein superfamily. Cell Mol Life Sci. 2011;68(24):3983–3993. doi: 10.1007/s00018-011-0768-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sorre B, et al. Nature of curvature coupling of amphiphysin with membranes depends on its bound density. Proc Natl Acad Sci USA. 2012;109(1):173–178. doi: 10.1073/pnas.1103594108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Frost A, et al. Structural basis of membrane invagination by F-BAR domains. Cell. 2008;132(5):807–817. doi: 10.1016/j.cell.2007.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mim C, et al. Structural basis of membrane bending by the N-BAR protein endophilin. Cell. 2012;149(1):137–145. doi: 10.1016/j.cell.2012.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shi Z, Baumgart T. Membrane tension and peripheral protein density mediate membrane shape transitions. Nat Commun. 2015;6:5974. doi: 10.1038/ncomms6974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Simunovic M, Voth GA, Callan-Jones A, Bassereau P. When physics takes over: BAR proteins and membrane curvature. Trends Cell Biol. 2015;25(12):780–792. doi: 10.1016/j.tcb.2015.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Simunovic M, Srivastava A, Voth GA. Linear aggregation of proteins on the membrane as a prelude to membrane remodeling. Proc Natl Acad Sci USA. 2013;110(51):20396–20401. doi: 10.1073/pnas.1309819110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Simunovic M, Voth GA. Membrane tension controls the assembly of curvature-generating proteins. Nat Commun. 2015;6:7219. doi: 10.1038/ncomms8219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Noguchi H. Membrane tubule formation by banana-shaped proteins with or without transient network structure. Sci Rep. 2016;6:20935. doi: 10.1038/srep20935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Traub LM. F-BAR/EFC domain proteins: Some assembly required. Dev Cell. 2015;35(6):664–666. doi: 10.1016/j.devcel.2015.12.003. [DOI] [PubMed] [Google Scholar]
- 16.McDonald NA, Vander Kooi CW, Ohi MD, Gould KL. Oligomerization but not membrane bending underlies the function of certain F-BAR proteins in cell motility and cytokinesis. Dev Cell. 2015;35(6):725–736. doi: 10.1016/j.devcel.2015.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhu C, Das SL, Baumgart T. Nonlinear sorting, curvature generation, and crowding of endophilin N-BAR on tubular membranes. Biophys J. 2012;102(8):1837–1845. doi: 10.1016/j.bpj.2012.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yu H, Schulten K. Membrane sculpting by F-BAR domains studied by molecular dynamics simulations. PLOS Comput Biol. 2013;9(1):e1002892. doi: 10.1371/journal.pcbi.1002892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cui H, et al. Understanding the role of amphipathic helices in N-BAR domain driven membrane remodeling. Biophys J. 2013;104(2):404–411. doi: 10.1016/j.bpj.2012.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ramesh P, et al. FBAR syndapin 1 recognizes and stabilizes highly curved tubular membranes in a concentration dependent manner. Sci Rep. 2013;3:1565. doi: 10.1038/srep01565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pang X, et al. A PH domain in ACAP1 possesses key features of the BAR domain in promoting membrane curvature. Dev Cell. 2014;31(1):73–86. doi: 10.1016/j.devcel.2014.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Renard HF, et al. Endophilin-A2 functions in membrane scission in clathrin-independent endocytosis. Nature. 2015;517(7535):493–496. doi: 10.1038/nature14064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Boucrot E, et al. Endophilin marks and controls a clathrin-independent endocytic pathway. Nature. 2015;517(7535):460–465. doi: 10.1038/nature14067. [DOI] [PubMed] [Google Scholar]
- 24.Kwok R, Evans E. Thermoelasticity of large lecithin bilayer vesicles. Biophys J. 1981;35(3):637–652. doi: 10.1016/S0006-3495(81)84817-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Derényi I, Jülicher F, Prost J. Formation and interaction of membrane tubes. Phys Rev Lett. 2002;88(23):238101. doi: 10.1103/PhysRevLett.88.238101. [DOI] [PubMed] [Google Scholar]
- 26.Yu S, et al. Identification of phospholipid molecular species in porcine brain extracts using high mass accuracy of 4.7 Tesla Fourier transform ion cyclotron resonance mass spectrometry. B Kor Chem Soc. 2006;27(5):793–796. [Google Scholar]
- 27.Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J. 2000;79(1):328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sorre B, et al. Curvature-driven lipid sorting needs proximity to a demixing point and is aided by proteins. Proc Natl Acad Sci USA. 2009;106(14):5622–5626. doi: 10.1073/pnas.0811243106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gallop JL, et al. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25(12):2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Capraro BR, et al. Kinetics of endophilin N-BAR domain dimerization and membrane interactions. J Biol Chem. 2013;288(18):12533–12543. doi: 10.1074/jbc.M112.435511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Simunovic M, Lee KY, Bassereau P. Celebrating Soft Matter’s 10th anniversary: Screening of the calcium-induced spontaneous curvature of lipid membranes. Soft Matter. 2015;11(25):5030–5036. doi: 10.1039/c5sm00104h. [DOI] [PubMed] [Google Scholar]
- 32.Prévost C, et al. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat Commun. 2015;6:8529. doi: 10.1038/ncomms9529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Morlot S, et al. Membrane shape at the edge of the dynamin helix sets location and duration of the fission reaction. Cell. 2012;151(3):619–629. doi: 10.1016/j.cell.2012.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Roux A, et al. Membrane curvature controls dynamin polymerization. Proc Natl Acad Sci USA. 2010;107(9):4141–4146. doi: 10.1073/pnas.0913734107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Peter BJ, et al. BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science. 2004;303(5657):495–499. doi: 10.1126/science.1092586. [DOI] [PubMed] [Google Scholar]
- 36.Chen H, et al. Epsin is an EH-domain-binding protein implicated in clathrin-mediated endocytosis. Nature. 1998;394(6695):793–797. doi: 10.1038/29555. [DOI] [PubMed] [Google Scholar]
- 37.Monnier S, Rochal SB, Parmeggiani A, Lorman VL. Long-range protein coupling mediated by critical low-energy modes of tubular lipid membranes. Phys Rev Lett. 2010;105(2):028102. doi: 10.1103/PhysRevLett.105.028102. [DOI] [PubMed] [Google Scholar]
- 38.Golushko IY, Rochal SB, Lorman VL. Complex instability of axially compressed tubular lipid membrane with controlled spontaneous curvature. Eur Phys J E Soft Matter. 2015;38(10):112. doi: 10.1140/epje/i2015-15112-6. [DOI] [PubMed] [Google Scholar]
- 39.Shlomovitz R, Gov NS, Roux A. Membrane-mediated interactions and the dynamics of dynamin oligomers on membrane tubes. New J Phys. 2011;13:065008. [Google Scholar]
- 40.Simunovic M, et al. Protein-mediated transformation of lipid vesicles into tubular networks. Biophys J. 2013;105(3):711–719. doi: 10.1016/j.bpj.2013.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sarić A, Cacciuto A. Fluid membranes can drive linear aggregation of adsorbed spherical nanoparticles. Phys Rev Lett. 2012;108(11):118101. doi: 10.1103/PhysRevLett.108.118101. [DOI] [PubMed] [Google Scholar]
- 42.Sundborger A, et al. An endophilin-dynamin complex promotes budding of clathrin-coated vesicles during synaptic vesicle recycling. J Cell Sci. 2011;124(Pt 1):133–143. doi: 10.1242/jcs.072686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Meinecke M, et al. Cooperative recruitment of dynamin and BIN/amphiphysin/Rvs (BAR) domain-containing proteins leads to GTP-dependent membrane scission. J Biol Chem. 2013;288(9):6651–6661. doi: 10.1074/jbc.M112.444869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Andersson F, Löw P, Brodin L. Selective perturbation of the BAR domain of endophilin impairs synaptic vesicle endocytosis. Synapse. 2010;64(7):556–560. doi: 10.1002/syn.20772. [DOI] [PubMed] [Google Scholar]
- 45.Ringstad N, et al. Endophilin/SH3p4 is required for the transition from early to late stages in clathrin-mediated synaptic vesicle endocytosis. Neuron. 1999;24(1):143–154. doi: 10.1016/s0896-6273(00)80828-4. [DOI] [PubMed] [Google Scholar]
- 46.Takei K, Slepnev VI, Haucke V, De Camilli P. Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis. Nat Cell Biol. 1999;1(1):33–39. doi: 10.1038/9004. [DOI] [PubMed] [Google Scholar]
- 47.Ferguson SM, et al. Coordinated actions of actin and BAR proteins upstream of dynamin at endocytic clathrin-coated pits. Dev Cell. 2009;17(6):811–822. doi: 10.1016/j.devcel.2009.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Daumke O, Roux A, Haucke V. BAR domain scaffolds in dynamin-mediated membrane fission. Cell. 2014;156(5):882–892. doi: 10.1016/j.cell.2014.02.017. [DOI] [PubMed] [Google Scholar]
- 49.Lee E, et al. Amphiphysin 2 (Bin1) and T-tubule biogenesis in muscle. Science. 2002;297(5584):1193–1196. doi: 10.1126/science.1071362. [DOI] [PubMed] [Google Scholar]
- 50.Karbowski M, Jeong SY, Youle RJ. Endophilin B1 is required for the maintenance of mitochondrial morphology. J Cell Biol. 2004;166(7):1027–1039. doi: 10.1083/jcb.200407046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Montes LR, Alonso A, Goñi FM, Bagatolli LA. Giant unilamellar vesicles electroformed from native membranes and organic lipid mixtures under physiological conditions. Biophys J. 2007;93(10):3548–3554. doi: 10.1529/biophysj.107.116228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cuvelier D, Derényi I, Bassereau P, Nassoy P. Coalescence of membrane tethers: Experiments, theory, and applications. Biophys J. 2005;88(4):2714–2726. doi: 10.1529/biophysj.104.056473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Helfrich W. Elastic properties of lipid bilayers: Theory and possible experiments. Z Naturforsch C. 1973;28(11):693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 54.Evans EA. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipet aspiration tests. Biophys J. 1983;43(1):27–30. doi: 10.1016/S0006-3495(83)84319-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Srivastava A, Voth GA. A hybrid approach for highly coarse-grained lipid bilayer models. J Chem Theory Comput. 2013;9(1):750–765. doi: 10.1021/ct300751h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117(1):1–19. [Google Scholar]
- 57.Noguchi H. Two- or three-step assembly of banana-shaped proteins coupled with shape transformation of lipid membranes. Europhys Lett. 2014;108(4) [Google Scholar]
- 58.Ramakrishnan N, Sunil Kumar PB, Ipsen JH. Membrane-mediated aggregation of curvature-inducing nematogens and membrane tubulation. Biophys J. 2013;104(5):1018–1028. doi: 10.1016/j.bpj.2012.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary File