Detecting interregionally diversifying natural selection on modern human cranial form by using matched molecular and morphometric data (original) (raw)
Abstract
This comparison of morphological and neutral genetic variation in 10 human populations was designed to test a neutral hypothesis of cranial evolution in living and recent humans and to explain deviations from neutrality where detected. Overall, among-population differences in extant Homo sapiens cranial morphology are proportional to among-population differences in neutral molecular characteristics. For most of the populations studied, cranial morphology varies among regions in a manner consistent with neutral expectations. Removal of the effects of shared population history and structure by using the partial Mantel's test, however, does not remove the correlation between some aspects of cranial morphology and a measure of coldness of climate. The excess differentiation is most apparent in those population comparisons that involve a Siberian population living in an extremely cold environment. This finding suggests the action of natural selection, associated with regional variation in temperature, leading to among-population differentiation in excess of neutral expectations for some cranial dimensions. Those dimensions reflect the breadth of the skull, cranial vault size and shape, and aspects of nasal morphology. Although morphology for most of the world appears to vary among populations in accordance with neutral expectations in the context of population structure and history, morphology of the Siberian population appears to have undergone adaptation by natural selection.
Extant Homo sapiens is a globally distributed species that occupies a wide variety of environments. Modern human biological diversity, both molecular and phenotypic, is often structured in space (1, 2). Candidate causes for the structure are neutral evolutionary forces of mutation, migration, and random genetic drift, as well as natural selection. If neutral forces of evolution shape diversity in a spatially structured species to the exclusion of natural selection, then the pattern of among-group differences will reflect population structure and history, defined here as the action of random genetic drift (including founder events resulting from range expansions as well as the sampling effects of finite local populations) and gene flow. Under certain conditions, interregionally diversifying natural selection generates differentiation among regions in excess of neutral expectations (3).
The cranium is one of the most commonly studied parts of the modern human phenotype. It is particularly important to understand the causes of among-group differentiation in human cranial characteristics because of the extensive use of modern human cranial variation as a benchmark for assessing hominid fossils. Craniometric characteristics are used extensively to study population structure and history in archaeological contexts (4, 5). Traditional craniometric studies have yielded a wealth of results that demonstrate correlations among aspects of cranial morphology and climate (6–10). These correlations with environment imply that dimensions of nasal and overall cranial morphology are subject to regionally diversifying natural selection driving different populations toward different local optima.
The partitioning of additive genetic variance into among- and within-region components indicates that the among-region proportion of additive genetic variance for cranial characteristics in humans is approximately what we would expect if craniometric diversity among regions is more or less neutral (11, 12). Furthermore, there is a significant degree of proportionality between among-region morphological and genetic differentiation (13). These observations suggest that neutral forces of evolution can largely explain among-region differentiation in cranial characteristics in H. sapiens. They also highlight the possibility that the observed correlation between aspects of human cranial morphology and climate variables could be due to a correlation of each with the neutral patterns of interregional difference generated by population history and structure (11, 14).
In this paper, I use an empirically derived model of population structure and history to test the hypothesis that neutral evolutionary forces are adequate to explain differences in cranial morphology among human populations. I then apply a correction for population history to assess the fit of cranial morphology to a putative selection pressure relating to the coldness of local climates. Population structure and history are analogous to phylogeny (except that they include the effects of lateral gene exchange through migration among populations, which is included under population structure), and phylogeny has long been recognized as a potentially confounding factor in studies of adaptation using interspecific comparisons (15, 16), which holds true for populations within a subdivided species as well (17). Populations that share recent common ancestry and/or exchange a large number of migrants should resemble one another more than geographically isolated and distantly related populations. Correlations between a putative selection pressure that is spatially distributed and patterns of biological diversity may be due to a correlation between population history and structure and the spatial distribution of the putative selection pressure. If the traits under study are selectively neutral, then among-region differences in the phenotypic characteristic and a plausible selective pressure should be uncorrelated once the effect of population history and structure has been removed.
Different types of natural selection have different effects on the patterns and magnitudes of deviations from neutral expectations of among-population variation. Among-region stabilizing selection keeps populations from diverging with respect to a suite of adaptive characteristics (3). Among-region diversifying selection results in divergence among populations in excess of neutral expectations. Globally stabilizing selection might be difficult to detect, because it cannot be differentiated from a scenario where there is a large amount of epistatic variance underlying individual differences in a characteristic (3). Dominance may increase the amount of additive genetic variance among populations in the absence of globally diversifying selection, but variation in morphological characteristics tends to have a substantial additive genetic basis (18).
_F_ST is the proportion of among-region genetic variance (19). _F_ST analogs can be estimated for quantitative characteristics, given that they vary among regions and among individuals in a manner adequately represented by an equal and additive effects model (3, 20–22). This allows the direct comparison of quantitative phenotypic and molecular genetic data. These approaches are appropriate, given the following:
- the biometrical characteristics under study have a substantial additive genetic component associated with differences among individuals and populations;
- the norms of reaction for the genotypes underlying the characteristics are reasonably flat with respect to the range of observed environments; and
- environmental effects are randomly distributed with respect to both individuals and groups.
Following the convention established by Spitze (20), I call an _F_ST estimated for additive genetic variance underlying variation in a phenotypic characteristic a _Q_ST to distinguish it from an _F_ST value calculated from molecular data.
If a quantitative characteristic varies neutrally among regions, its _Q_ST estimate should equal the _F_ST estimated by using neutral genetic loci (3). A _Q_ST value calculated on the basis of characteristics that have been subjected to interregionally diversifying natural selection will be higher than an _F_ST value calculated by using many neutral genetic loci, given that there is a substantial additive genetic component to the phenotypic variance of the characteristic under study. The difference between _F_ST and _Q_ST reflects the cumulative effect of interregionally diversifying natural selection. It follows from these observations that a matrix of neutral genetic _F_ST distances will be proportional to a matrix of neutral quantitative genetic _Q_ST distances (23). Furthermore, deviations from proportionality should occur only when a selection pressure is distributed among regions in a way not proportional to the _F_ST distance matrix.
There is strong evidence that variation within local populations of humans is moderately to highly heritable (24). External head measurements have narrow sense heritabilities between ≈0.45 and ≈0.65, with an average of ≈0.55 (24). There are several indicators that among-region differences in cranial form, at least in part, are due to the effects of heredity. Immigrants to the U.S. preserve morphological affinities with their source populations, and their children do not converge to some new environmentally mediated distribution of phenotypes (25). Furthermore, there is a significant correlation between the patterns of morphological distance and genetic distances among populations, indicating that morphological distances are reflections of genetic differences (13).
Materials and Methods
All cranial data used in this study were from Howells' (2) globally distributed craniometric dataset of 2,472 individuals from 28 different populations. I used 57 linear measurements taken on each cranium from 955 individuals from 10 populations that I thought I could match to genetic data. Rosenberg et al. (26) report data on 377 microsatellite loci from 52 different populations. I chose to use 413 individuals from those populations that I thought were sufficiently close with respect to geographic origin and/or linguistic similarity to individual samples from Howells' data set. In this case, the microsatellite data were the limiting factors, and I chose to retain 10 populations (Table 1). Henceforth, I refer to the composite samples by the names listed in Table 1, column 1, followed by one of Howells' designations in parentheses. I refer to individual craniometric measurements by Howells' abbreviations (2), a list of which is provided in Table 4, which is published as supporting information on the PNAS web site. Where populations sampled for genetic and craniometric data are located on the periphery of the geographic distribution of the study and are rather distant from the remaining populations, the specific morphological and genetic match should not impact the results of the study very much, so long as only one match is made. Thus in the case of the South American sample, whereas the genetic and morphological populations are from either side of the Andes, they are both roughly the same geographic distance from all of the other populations in the sample. A similar logic was applied to the European sample. Because none of the genetic and cranial samples were from the same specific location, and because the samples all came from a fairly restricted geographic area, I chose the Medieval Norse population, because it was the largest in terms of the number of individuals measured and the least complicated in terms of assigning sex to the individual crania (2).
Table 1.
Summary of geographic and ethnic affiliation of cranial (Howells, ref. 2) and genetic (Rosenberg et al., ref. 26) data and geographic location of stations providing temperature data
| Population | Howells (n) | Rosenberg et al. (n) | Weather station |
|---|---|---|---|
| South America | Yauyos (110) | Karatiana, Surui, and Columbian (58) | Pisco, Peru |
| China | Anyang (42) | Han (35) | Chan-Chih, People's Republic of China |
| Japan | North Kyushu (91) | Japanese (32) | Fukuoka, Japan |
| Siberia | Buriats (109) | Daur, Mongolian, and Tu (30) | Irkutsk, Russia |
| Europe | Medieval Norse (110) | French, Italian, and Tuscan (50) | Oslo, Norway |
| Middle East | Gizeh (111) | Palestinian and Bedouin (100) | Cairo, Egypt |
| Melanesia | Tolai (83) | Melanesian and Papuan (39) | Rabul, Papua New Guinea |
| East Africa | Telta (83) | Bantu Kenya (12) | Voi, Kenya |
| South Africa | Bushman/San (90) | San (7) | Keetmanshop, Namibia |
| West Africa | Dogon (99) | Yoruba and Mandenka (49) | Mopti/Barbe, Mali |
Mismatches between cranial and genetic samples where both types of data are not collected on the same individuals introduce error into any comparison of genetic and morphological distance. This error will tend to reduce the magnitude of their association. Estimates of the strength of the correlation between the matrices must then be regarded as minimum estimates.
I calculated Slatkin's _R_ST (_F_st, estimator for use with DNA repeat data) (27) in a pairwise fashion between all populations to create a model of neutral evolutionary population history (F, genetic distance matrix). Slatkin's _R_ST is an _F_ST estimator specifically designed for microsatellite polymorphisms (27). I used the Relethford–Blangero (22) estimator to generate a matrix of pairwise _Q_ST values (Q, morphological distance matrix) between populations, taking into account the covariances among the measurements. This procedure treats _F_ST or _Q_ST as a genetic distance and is distinct from using the off-diagonal elements of the R matrix obtained by using the Relethford–Blangero method (22). I transformed each measurement into z scores within each sex to minimize the impact of size-related sexual dimorphism and to conform to the assumptions of the Relethford–Blangero estimator. The Relethford–Blangero estimator requires an estimate of the additive genetic covariance matrix (G). I used a scaled pooled phenotypic covariance matrix (P) to calculate _Q_ST values. Because P and G tend to be proportional to one another in mammals for morphological characteristics, and P is a good working approximation of G (28), I followed the recommendation of Relethford and Blangero (22) and scaled P estimated from the data by scaling the matrix by an estimate of the average heritability (_h_2, proportion of phenotypic variance associated with additive genetic effects) of craniometric measurements to estimate G. To assess the impact of different assumptions about _h_2, I replicated the analysis by using different values of heritability ∈ (0.55,1). For both F and Q, I used an arcsine-root transformation to rescale each genetic distance, because both _F_ST and _Q_ST are ratios (23). Additionally, I calculated _Q_ST values for each of the individual measurements and the entire data set, correcting for differences in sample size, to assess the extent to which both the individual measurements and the entire cranium vary among regions. I constructed a hypothesis of a selective pressure (S, temperature distance matrix) by calculating the squared pairwise differences in the mean temperature during the coldest month of the year among different populations. Some weather stations from a global climate dataset (29) were sufficiently close to the locations of each of Howells' populations used here to provide temperature data to build a selective hypothesis (Table 1).
To assess the level of association between each of the matrices used in this analysis, I used Mantel's matrix correlation statistic. I used the partial Mantel's matrix correlation statistic to control for the effects of population structure and history when comparing Q and S (23, 30). To assess the significance of the correlation between selected matrices, I used 10,000 random matrix rearrangements to estimate the one-tailed probability that the observed matrix correlation was stronger than a given random matrix correlation. To limit the chance of obtaining statistically significant results because of multiple testing, the Bonferroni correction was applied to modify the standard for significance (nominally α = 0.050, adjusted to 0.017).
To identify individual populations that contribute disproportionately to deviations from neutrality, I calculated the matrix correlation statistics 10 additional times, each time deleting one of the individual populations without performing additional tests. If evolutionary forces and sampling error act uniformly on the magnitude of each of the matrix elements, then the deletion of any individual population should not substantially change the results. If natural selection acts on only a few populations, making them excessively divergent, the removal of one or all of those populations should result in an improvement of fit between F and Q, as ascertained using the Mantel's matrix correlation statistic.
To assess the extent to which the individual measurements impact the overall fit between matrices, I calculated the matrix correlations of Q matrices constructed using each individual cranial measurement vs. the S matrix and the F matrix to identify those individual measurements most strongly associated with the hypothesized selective pressure and population structure and history, respectively.
Deviations from neutral expectations could be a result of correlated response by several correlated measurements or by a common response across several less-correlated regions of the cranium. Because one minus a correlation coefficient is a simple measure of dissimilarity or distance, I calculated a pooled correlation matrix from the _z_-scored original variables and subtracted each element from one. I applied principal coordinates (PCO) analysis to the resulting measurement distance matrix to search for dependencies between variables. The position of individual measurements on the PCOs should provide a rough indication of the extent to which measures are likely to exhibit a common response due to morphological integration or if an observed common response is due to several weakly genetically correlated parts of the cranium exhibiting a common response to a particular selection pressure. To decide whether deviations from neutral expectations were a result of evolution in overall size of the cranium, I calculated the log geometric mean of all variables for each individual and calculated the strength of the correlations between log size and the logged original variables. The geometric mean of all measurements on an organism is a standard proxy for overall size (31). I used only males (more numerous than females in this sample) when looking for size dependencies to avoid the confounding effects of size-related sexual dimorphism. I then plotted these correlations with log size against the Q for that individual measurement vs. S controlling for F partial Mantel's score, which is an indicator of the extent to which cold-mediated natural selection is acting on that particular dimension. There will be a detectable association between these measurements if changes in overall size are driving the measurements. All analyses were conducted in matlab (The Math Works, Natick, MA), using programs written by the author or from the res package (R. E. Strauss, Texas Tech University, Lubbock, TX) and spot error checked using Relethford's rmet program (J. H. Relethford, State University of New York, Oneonta, NY).
Results
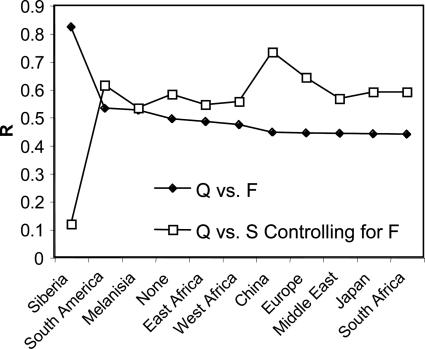
I report Mantel's matrix correlation statistics for the comparisons of Q vs. F and Q vs. S and the partial Mantel's matrix correlation statistic for Q vs. S controlling for F and their associated probabilities as assessed through 10,000 matrix randomizations in Table 2. All comparisons are significant after Bonferroni correction. Additionally, the removal of population history appears to improve the correlation between Q and S. The different _h_2 values used in this analysis did not appreciably change the results, and I report results for _h_2 = 1 (yielding minimum _Q_ST values) for all matrix comparisons. Systematic removal of individual populations revealed that removing the Siberian (Buriat) population substantially improved the correlation of the Q and F matrices and substantially reduced the magnitude of correlation of the Q vs. S comparison controlling for F (Fig. 1).
Table 2. Results of Mantel's and partial Mantel's tests of R among Q, F, and S.
| Comparison | R | P* |
|---|---|---|
| Q vs. F | 0.4949 | 0.0064 |
| Q vs. S | 0.4866 | 0.0094 |
| Q vs. S controlling for F | 0.5825 | 0.0085 |
Fig. 1.
The impact of the removal of individual populations from the analysis. The abscissa consists of those populations removed from a given analysis along with the full analysis ordered in terms of the strength of their F vs. Q association represented as Mantel's R on the ordinate. The removal of those populations to the left of the abscissa entry “None” results in higher associations of F and Q than the full analysis, and the removal of those to the right results in lower associations of F and Q. As a means to provide a qualitative assessment of the impact of individual populations on the overall analysis rather than a quantitative comparison of the strength of different evolutionary forces, Mantel's R of Q vs. S controlling for E is also represented.
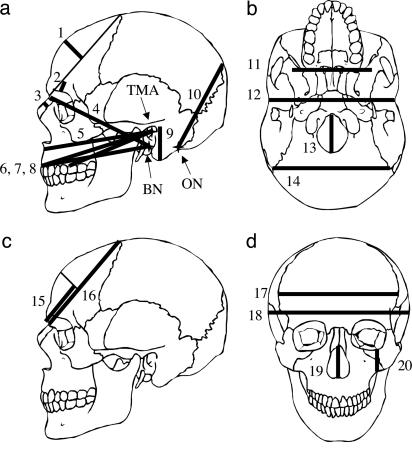
Fig. 2 highlights the approximate locations of the measures that are highly associated with F and S on representations of the skull. Fig. 2_a_ shows the measurements that have Q matrices that are highly associated with F. The measurements tend to rest on or parallel to the midline sagittal plane. This contrasts sharply with the measurements that are highly associated with S, which tend to reflect breadth (Fig. 2 b–d). I report only the top 10 most highly associated measurements in Fig. 2. I report the Mantel's statistic for matrix comparisons between Q matrices calculated using each individual measurement against F and the partial Mantel's statistic for each measurement's Q matrix vs. S controlling for F in Table 4.
Fig. 2.
Superimposition of some cranial measurements tabulated in Table 3 onto a generic representation of the human cranium. (a) Ten measurements that have individually calculated Q matrices that are highly associated with F. (b_–_d) Ten measurements that have individually calculated Q matrices that are highly associated with S. Some measurements (i.e., NLH) have been abstracted slightly from their true positions for clarity. Thick lines represent the actual measurements, and thin lines represent lines of reference from which the actual measurements are taken. Relevant osteometric points that are obscured by intervening structures are labeled (TMA, transmeatal axis; BN, basion; and ON, opisthion). Measurements: 1, nasion-bregma subtense; 2, supraorbital projection; 3, simonic subtense; 4, basion-nasion length; 5, subspinale radius; 6, prosthion radius; 7, basion-prosthion length; 8, molar alveolus radius; 9, mastoid height; 10, λ-opisthion chord; 11, minimum cranial breadth; 12, biauricular breadth; 13, foramen magnum length; 14, biasterionic breadth; 15, nasion-subtense fraction; 16, nasion-bregma chord; 17, maximum frontal breadth; 18, maximum cranial breadth; 19, NLH; 20, cheek height.
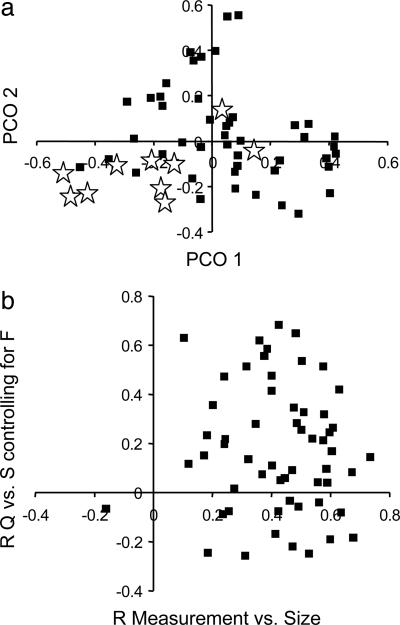
The results of the PCO analysis of M are displayed in Fig. 3_a_. The first PCO accounts for 15.2% of the variation and distinguishes measures of breadth from measures of length and facial projection. The second PCO accounts for 10.6% of the variation and distinguishes nasal and facial measurements from measures on the remainder of the cranium. Measurements highly associated with S controlling for F are moderately clustered, indicating that the observed patterns are not the result of a single correlated response. There is no apparent correlation between the degree of a measurement's Q vs. S correlation and an individual measurement's correlation with size, as represented by the log geometric mean of all variables for each individual (Fig. 3_b_).
Fig. 3.
The impact of overall cranial size on the detection of deviations from neutrality. (a) A PCO of the correlation compliment matrix; a plot of PCO 1 vs. PCO 2. Starred measurements are those that have high individual Q vs. S associations controlling for F. (b) A plot of the partial Mantel's statistic (R) for the Q matrix for each measurement vs. the S matrix controlling for F vs. the correlation of each measurement with the log geometric mean of each individual. Only results for males are presented to control confounding effects of size-related sexual dimorphism.
Estimates of _R_ST for the microsatellite data and _Q_ST for the craniometric data for all of the populations combined are reported in Table 3 for different assumptions of heritability. _R_ST for microsatellites is typical for autosomal polymorphisms (_R_ST = 0.11), and all estimates of _Q_ST exceed the _R_ST estimate. Given that the equal, additive, and infinitesimal effects model adequately represents the within- and among-region differences in morphology, and that average _h_2 for cranial measurements is ≈0.55, these results show that the effects of natural selection account for about one-half of the among-region additive genetic variance.
Table 3. Estimates of _R_ST and _Q_ST given different assumptions about heritability.
| Type | Estimate* | Assumptions of _h_2 |
|---|---|---|
| _R_ST | 0.11 | N/A |
| _Q_ST | 0.14 | _h_2 = 1 |
| _Q_ST | 0.24 | _h_2 = 0.55 |
Discussion
These results indicate that population history has a significant effect on the pattern of among-region differences in modern human cranial form. This is consistent with the results of Relethford (11, 12) and Gonzalez-Jose et al. (13). Unlike these previous studies, however, these results show that natural selection may be important in shaping among-population differences in cranial morphology, as indicated by the strong association of morphological differences among populations with differences in mean temperature during the coldest month of the year once population history is removed. This pattern is apparent only when the Siberian (Buriat) sample is included. The fit between Q and S improves once F is removed. Likewise, that _Q_ST scores calculated using different assumptions about heritability are uniformly larger than _R_ST scores suggests the action of among-region diversifying natural selection (Table 3).
That measures of cranial breadth contribute to the observed departures from neutral expectations, coupled with the observation that measures of cranial length (glabella-occipital length, nasio-occipital length) tend not to vary much among regions (see Table 4), is consistent with the hypothesis that there is natural selection for a thermoregulatory capacity in colder environments, resulting in brachycephalization (6, 7). This thermoregulatory hypothesis is further bolstered by the fact that the removal of the Siberian (Buriat) population from the analysis eliminates the association between the population history-corrected morphological distances and the differences among populations with respect to mean temperature during the coldest month of the year.
Measures of nasal height (NLH) are also strongly associated with S (nasion-prosthion height is also highly associated but not depicted in Fig. 2), which is consistent with the thermoregulatory breathing hypotheses used to explain among-region differences in nasal morphology and the nasal index (NLH/nasal breadth × 100) in particular (9). The hypothesis that the nasal index is shaped by natural selection in response to temperature is further bolstered by the fact that, whereas Q for the height of nasal aperture (NLH) associates strongly and positively with S controlling for F, the breadth of nasal aperture associates negatively, although less strongly, with S (see Table 4). This indicates that the two measures vary in opposite directions when compared to S, leading to tall narrow noses at one extreme (cold) and short broad noses at the other (hot). This is further evidence that differences in shape contribute to deviations from neutral expectations in addition to general changes in size.
Measurements with among-region patterns of variation that are highly concordant with among-region neutral genetic differences (Fig. 2_a_) include measurements that reflect the positioning of the face relative to the basicranium, nasal, brow, and neuro- and basicranial shape and size. The measurements that reflect the relative degree of midfacial and alveolar prognathism are similar to those dimensions that most differentiate anatomically modern humans from Neandertals (32).
The observed degree of correlation between F and Q must be regarded as a minimum estimate of the impact of population history and structure on among-population morphological differentiation because of the mismatches between the morphological and genetic samples in both time and space. For instance, the Middle Eastern (Gizeh) sample is ≈2,500 years old (2). These deviations in time and space do not appear to substantially impact the results of this analysis (see Fig. 1). Ideally, unrelated individuals in a given population would be sampled for both morphometric data and genetic material, whereas additive genetic covariance matrices for the morphometric measurements would be calculated from large pedigrees from each of the sampled populations. The temperature data used here were collected during the latter half of the 20th century and are not exactly representative of long-term climate. This should not substantially alter the results of this analysis so long as the various regions were proportionally colder or hotter relative to the present. If individual regions vary idiosyncratically with respect to their mean temperature during the coldest month of the year, then the Q vs. S comparison would be weakened.
Caution is warranted before ascribing too much weight to the specific morphological conclusions in this paper. The individuals in the other extreme cold environment population in the Howells data set, Greenland Inugsuk Eskimos (Howells' original designation), do not have particularly broad crania (2). If the Greenland sample were included in the analysis, the particular measurements that showed the highest correlations with the selective hypothesis in the absence of the effects of population history and structure could change. The particular model of selection presented here is admittedly simple and unlikely to cover all circumstances. Environmental conditions impacting the development of individuals may also explain the Siberian (Buriat) morphological departure from neutral expectations. The environmental effects, however, would have to be extreme to explain excess differentiation from the rest of the world. In either case, the Siberians' (Buriat) excess differentiation represents a departure from the neutral additive model of individual and population differences used in this analysis.
Both population history/structure and natural selection appear to have shaped the among-region differences observed in the modern human cranium, as represented in these 10 populations taken from Howells' data set. Population history and structure seem to predominate in shaping among-region differences among the nine non-Siberian (Buriat) modern human populations. This is in close agreement with Relethford's (11, 12, 33) analyses. However, when the Siberian (Buriat) population is included in the analysis, cold-mediated natural selection appears to be primarily responsible for the large differences observed between the Siberian (Buriat) sample and the rest of the world. Another analysis by Relethford has also noted associations of craniometric variation with temperature controlling for geographic distance, further bolstering the secondary effect of natural selection on the global distribution of cranial variation (34). This raises the intriguing question of the limits of human cultural buffering when facing the challenges of extreme environments.
Supplementary Material
Supporting Table
Acknowledgments
I thank W. W. Howells for generously making publicly available craniometric data and N. A. Rosenberg for doing likewise with microsatellite data. T. D. Weaver, J. L. Mountain, R. G. Klein, S. Holmes, J. H. Jones, D. DeGusta, the Stanford Paleogroup, and an anonymous reviewer provided valuable feedback. John Relethford also reviewed the manuscript, and I thank him for his comments and for access to his in-press articles. Any errors and omissions are my own.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: PCO, principal coordinate; NLH, nasal height.
References
- 1.Cavalli-Sforza, L. L., Menozzi, P. & Piazza, A. (1994) The History and Geography of Human Genes (Princeton Univ. Press, Princeton, NJ).
- 2.Howells, W. W. (1989) Papers of the Peabody Museum of Archaeology and Ethnology (Harvard University, Cambridge, MA), Vol. 79.
- 3.Whitlock, M. C. (1999) Genet. Res. 74**,** 215–221. [DOI] [PubMed] [Google Scholar]
- 4.Konigsberg, L. W. (1988) Am. J. Phys. Anthropol. 77**,** 471–482. [DOI] [PubMed] [Google Scholar]
- 5.Konigsberg, L. W. (1990) Hum. Biol. 62**,** 49–70. [PubMed] [Google Scholar]
- 6.Beals, K. L., Smith, C. L. & Dodd, S. M. (1983) Am. J. Phys. Anthropol. 62**,** 425–437. [DOI] [PubMed] [Google Scholar]
- 7.Beals, K. L., Smith, C. L. & Dodd, S. M. (1984) Curr. Anthropol. 25**,** 301–330. [Google Scholar]
- 8.Carey, J. W. & Steegmann, A. T. (1981) Am. J. Phys. Anthropol. 56**,** 313–319. [DOI] [PubMed] [Google Scholar]
- 9.Franciscus, R. G. & Long, J. C. (1991) Am. J. Phys. Anthropol. 85**,** 419–427. [DOI] [PubMed] [Google Scholar]
- 10.Guglielmino-Matessi, C. R., Gluckman, P. & Cavallisforza, L. L. (1979) Am. J. Phys. Anthropol. 50**,** 549–564. [DOI] [PubMed] [Google Scholar]
- 11.Relethford, J. H. (1994) Am. J. Phys. Anthropol. 95**,** 53–62. [DOI] [PubMed] [Google Scholar]
- 12.Relethford, J. H. (2002) Am. J. Phys. Anthropol. 118**,** 393–398. [DOI] [PubMed] [Google Scholar]
- 13.Gonzalez-Jose, R., Van der Molen, S., Gonzalez-Perez, E. & Hernandez, M. (2004) Am. J. Phys. Anthropol. 123**,** 69–77. [DOI] [PubMed] [Google Scholar]
- 14.Relethford, J. H. & Harpending, H. C. (1994) Am. J. Phys. Anthropol. 95**,** 249–270. [DOI] [PubMed] [Google Scholar]
- 15.Felsenstein, J. (1985) Am. Nat. 125**,** 1–15. [Google Scholar]
- 16.Harvey, P. H. & Pagel, M. D. (1991) The Comparative Method in Evolutionary Biology (Oxford Univ. Press, Oxford, U.K.).
- 17.Mace, R. & Pagel, M. (1994) Curr. Anthropol. 35**,** 549–564. [Google Scholar]
- 18.Lopez-Fanjul, C., Fernandez, A. & Toro, M. A. (2003) Genetics 164**,** 1627–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wright, S. (1951) Ann. Eugenet. 15**,** 323–354. [DOI] [PubMed] [Google Scholar]
- 20.Spitze, K. (1993) Genetics 135**,** 367–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Merila, J., Kruuk, L. E. B. & Sheldon, B. C. (2001) J. Evol. Biol. 14**,** 918–929. [Google Scholar]
- 22.Relethford, J. H. & Blangero, J. (1990) Hum. Biol. 62**,** 5–25. [PubMed] [Google Scholar]
- 23.Storz, J. F. (2002) Mol. Ecol. 11**,** 2537–2551. [DOI] [PubMed] [Google Scholar]
- 24.Devor, E. J. (1987) J. Craniofacial Genet. Dev. Biol. 7**,** 95–106. [PubMed] [Google Scholar]
- 25.Sparks, C. S. & Jantz, R. L. (2002) Proc. Natl. Acad. Sci. USA 99**,** 14636–14639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rosenberg, N. A., Pritchard, J. K., Weber, J. L., Cann, H. M., Kidd, K. K., Zhivotovsky, L. A. & Feldman, M. W. (2002) Science 298**,** 2381–2385. [DOI] [PubMed] [Google Scholar]
- 27.Slatkin, M. (1995) Genetics 139**,** 1463–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cheverud, J. M. (1988) Evolution (Lawrence, Kans.) 42**,** 958–968. [DOI] [PubMed] [Google Scholar]
- 29.U.S. Federal Climate Complex (1996) International Station Meteorological Climate Summary (Dept. of the Navy/Dept. of Commerce/Dept. of the Air Force, Ashville, NC).
- 30.Smouse, P. E., Long, J. C. & Sokal, R. R. (1986) Syst. Zool. 35**,** 627–632. [Google Scholar]
- 31.Darroch, J. & Mosimann, J. (1985) Biometrika 72**,** 241–252. [Google Scholar]
- 32.Krovitz, G. E. (2003) in Patterns of Growth and Development in the Genus Homo, eds. Thompson, J. L., Krovitz, G. E. & Nelson, A. J. (Cambridge Univ. Press, Cambridge, U.K.), pp. 320–342.
- 33.Relethford, J. H. (2004) Hum. Biol., in press.
- 34.Relethford, J. H. (2004) Am. J. Hum. Biol. 16**,** 379–386. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Table