Membrane dynamics of dividing cells imaged by lattice light-sheet microscopy (original) (raw)
Lattice light-sheet microscopy is used to examine two problems in membrane dynamics—molecular events in clathrin-coated pit formation and changes in cell shape during cell division. This methodology sets a new standard for imaging membrane dynamics in single cells and multicellular assemblies.
Abstract
Membrane remodeling is an essential part of transferring components to and from the cell surface and membrane-bound organelles and for changes in cell shape, which are particularly critical during cell division. Earlier analyses, based on classical optical live-cell imaging and mostly restricted by technical necessity to the attached bottom surface, showed persistent formation of endocytic clathrin pits and vesicles during mitosis. Taking advantage of the resolution, speed, and noninvasive illumination of the newly developed lattice light-sheet fluorescence microscope, we reexamined their assembly dynamics over the entire cell surface and found that clathrin pits form at a lower rate during late mitosis. Full-cell imaging measurements of cell surface area and volume throughout the cell cycle of single cells in culture and in zebrafish embryos showed that the total surface increased rapidly during the transition from telophase to cytokinesis, whereas cell volume increased slightly in metaphase and was relatively constant during cytokinesis. These applications demonstrate the advantage of lattice light-sheet microscopy and enable a new standard for imaging membrane dynamics in single cells and multicellular assemblies.
INTRODUCTION
Quantitative analysis of membrane dynamics has depended on advances in the sensitivity and resolution of optical live-cell imaging. The lattice light-sheet microscope (LLSM) is the most recent of these developments (Chen et al., 2014; Gao et al., 2014). The excitation illumination in an LLSM is confined to a very thin plane, and the emitted fluorescence signal is observed along an optical axis orthogonal to the illumination plane. Exposure (and consequent photodamage) is thus restricted to the thin slice of the cell being imaged at any moment, and the image is uncorrupted by out-of-focus signal. The thinness of the light sheet also contributes to better axial resolution than in confocal microscopy. Rapid scanning through the sample yields a three-dimensional (3D) movie with millisecond time resolution per imaging plane. We describe here the use of this new technology to reexamine two problems in membrane dynamics—molecular events in clathrin-coated pit formation and changes in cell shape during cell division. We extended the latter studies to include observations within an intact biological tissue.
Membranes determine the compartmental organization of a cell. Their remodeling is an essential part of any change in cell size and shape and of any transfer of components to and from the surface and membrane-bound organelles, processes particularly critical during cell division. During mitosis, adherent cells round up, and the dramatic changes in cell shape associated with the birth of two cells from one require control of endocytosis and exocytosis for retrieval and recovery of components at the cell surface.
In our previous work, we analyzed BSC1 cells undergoing division using live-cell spinning-disk confocal fluorescence microscopy imaging and found that the dynamics of endocytic clathrin-coated pits in naturally dividing cells was unaffected at the bottom (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013) and probably also throughout the top surfaces (Tacheva-Grigorova et al., 2013).
These observations were restricted, by technical necessity, to the region of contact between the plasma membrane and the glass coverslip. Essentially no quantitative information that follows the dynamic process in living cells was available at all locations away from the coverslip because of the challenges of making these measurements in an accurate, rapid, and noninvasive manner while at the same time preventing the significant photobleaching inherent in the data acquisition protocol over the required time period (tens of minutes) and with high sampling frequency (every 2–3 s).
In the work reported here, we circumvented these problems by using LLSM to evaluate the dynamics of plasma membrane coated pit formation over the entire cell surface, allowing us to extend conclusions drawn from total internal reflection fluorescence (TIRF) microscopy imaging of the bottom surface (Saffarian and Kirchhausen, 2008; Saffarian et al., 2009; Cocucci et al., 2012; Aguet et al., 2013; Merrifield and Kaksonen, 2014). Using gene-edited SUM AP-2.1 cells expressing physiological levels of the endocytic clathrin adaptor AP-2 fluorescently tagged with enhanced GFP (eGFP) at its σ2 subunit to map endocytic pits and vesicles (Kural et al., 2015), we found no differences in the mean lifetimes or maximum intensities of coated pits assembling on the top and bottom surfaces of interphase cells. During mitosis, clathrin-coated pits continued to form, as we reported previously (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013). The new measurements, however, revealed a transient drop in pit density of ∼50% but no alteration in pit dynamics during metaphase and anaphase, with recovery back to interphase density during cytokinesis.
Entry into metaphase and initiation of cytokinesis appear to be two critical points for regulating molecular events redirecting exocytic membrane traffic associated with plasma membrane organization (Boucrot and Kirchhausen, 2007). We proposed that adjustment of endosomal recycling during cell division controls the cell area, leading to a sharp decrease during metaphase and recovery in anaphase (Boucrot and Kirchhausen, 2007). This modulation results in transient endosomal retention of membrane-bound proteins such as the transferrin receptor, explaining its acute depletion from the surface of cells as determined by fluorescence microscopy (Boucrot and Kirchhausen, 2007) and probably also the disappearance from the cell surface of many other membrane-bound proteins as determined by mass spectrometry (Ozlu et al., 2014).
A number of methods have been used to follow changes in cell shape, particularly during mitosis of cells grown in culture. The most recent applications include fluorescence exclusion with quantitative phase microscopy to determine cell volume (Zlotek-Zlotkiewicz et al., 2015), atomic force microscopy of uniaxially confined cells to calculate cell volume based on diameter and shape (Stewart et al., 2011; Fischer-Friedrich et al., 2014), suspended microchannel resonator of single cells to determine their volume (Grover et al., 2011; Son et al., 2015), and detection of the cell boundary computed from confocal sections to determine cell volume and area (Boucrot and Kirchhausen, 2007; Habela and Sontheimer, 2007). Quantitative determination of the volume and surface area of single cells in tissues remains challenging.
We show here that full-cell 3D imaging using LLSM facilitates measurement of cell surface area and cell volume and of their changes throughout the cell cycle, not only for cells in culture, but also for those in intact tissue—in our case, the developing eye and the spinal tissue of a zebrafish embryo. The surface area was smallest during mitosis and remained relatively constant during metaphase, anaphase, and telophase, as shown previously (Boucrot and Kirchhausen, 2007). After birth of the two daughter cells, the total surface increased rapidly during the transition from telophase to early stages of cytokinesis and then remained relatively constant until abscission. The rapid increase in surface area was accompanied by plasma membrane blebbing, as previously described for adherent and nonadherent cells (Boucrot and Kirchhausen, 2007). The greater axial resolution of the new measurements eliminates a curious outcome of our earlier work on cell volume during mitosis using spinning-disk confocal microscopy (Boucrot and Kirchhausen, 2008): the inaccuracy in estimating the volume of the flattened part of an interphase cell from a spinning-disk confocal microscope led to an apparent decrease in volume during mitosis. In the measurements reported here, the cell volume slightly increased during metaphase, in agreement with recent observations obtained with alternative methods (Son et al., 2015; Zlotek-Zlotkiewicz et al., 2015), and then remained relatively constant during cytokinesis (determined as the combined volume of the two daughter cells).
The applications of LLSM described here show that its resolution, speed, and noninvasiveness enable a new standard for imaging membrane dynamics in both single cells and multicellular assemblies.
RESULTS
Gene-edited SUM-AP-2.1 cells
Most previous work on coated-pit dynamics required ectopic expression of one or more molecular components of the structures being studied fused with a genetically encoded fluorophore (e.g., one of the many derivatives of GFP). The tendency for overexpression of the tagged protein in such cases and its unknown ratio relative to untagged, endogenous protein complicates substantially any quantitative analysis. Gene editing, which can replace all alleles with the tagged protein in question, circumvents both these problems, achieving physiological expressions levels and eliminating untagged copies of the target (Doyon et al., 2011; Cocucci et al., 2014; Grassart et al., 2014; Hong et al., 2015; Kural et al., 2015).
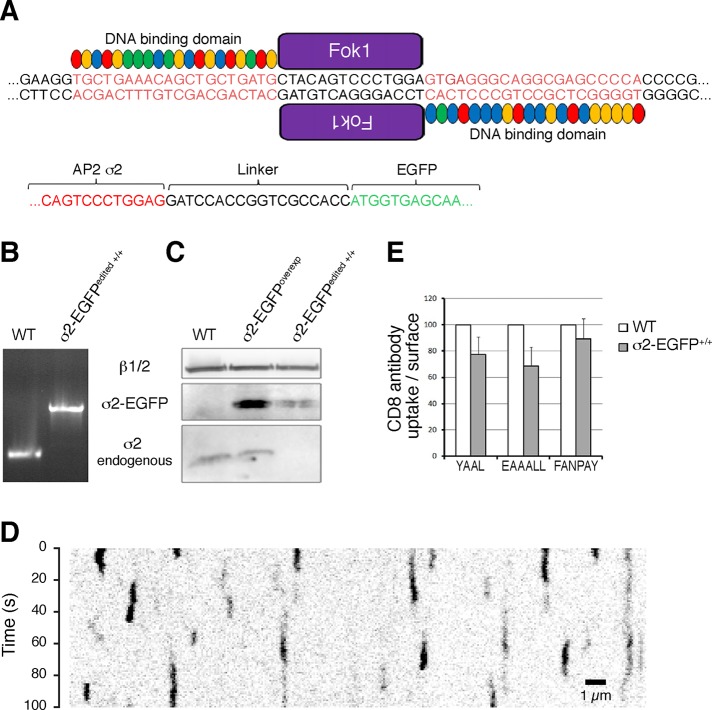
We gene edited SUM159 human breast cancer–derived cells to modify both AP-2 σ2 alleles with AP-2 σ2-eGFP (cell line SUM-AP-2.1), using a transcription activator–like effector nuclease (TALEN)–mediated editing strategy (Sanjana et al., 2012; Cocucci et al., 2014; Kural et al., 2015). We replaced the AP-2 subunit σ2 with σ2-eGFP, in which the C-terminus of σ2 is joined to eGFP by a six-residue linker with sequence DPPVAT (Figure 1A). PCR analysis of genomic DNA showed substitution of both alleles and absence of DNA encoding wild-type σ2 (Figure 1B). Western blot analysis confirmed substitution of σ2 by σ2-eGFP (Figure 1C). The kymograph from a time series in which we imaged fluorescent coated pits and vesicles with TIRF microscopy at the bottom surface of the SUM-AP-2.1 cells (Figure 1D) shows that AP-2–eGFP was in diffraction-limited structures exhibiting the dynamic behavior of canonical clathrin/AP-2–coated pits (Ehrlich et al., 2004; Taylor et al., 2011; Cocucci et al., 2012). Long-lived structures ascribed to persistent clathrin-AP-2 “coated plaques” (Saffarian et al., 2009; Chen et al., 2014) were virtually absent.
FIGURE 1:
Characterization of gene-edited SUM159-AP-2.1 cells expressing σ2-eGFP. (A) Schematic representation of the gene-editing strategy based on the TALEN approach used to incorporate eGFP at the C-terminus of the σ2 subunit of AP-2. The genomic DNA regions highlighted in red correspond to the sequences recognized by the DNA-binding domain of the TALEN repeats fused to the Fok1 endonuclease. The linker sequence generated upon homologous recombination between the eGFP and σ2 is shown. (B) Genomic PCR analysis demonstrating the biallelic integration of the eGFP sequence to the σ2 locus in the genome-edited cell line σ2-eGFP+/+ (here named SUM-AP-2.1). The single PCR product obtained in the genome-edited cell line was larger than the corresponding product obtained in the parental SUM159 cells (WT) using the same set of PCR probes. (C) Immunoprecipitation with the monoclonal antibody specific for β1/β2 of AP-2 (Clairmont et al., 1997) from cell-free lysates obtained from SUM159 cells (WT), stably expressing σ2-eGFP (σ2-eGFPoverexp), or genome-edited (σ2-eGFPedited+/+), followed by Western blot analysis with an antibody specific for σ2. The data show presence of σ2-eGFP and undetectable amounts of nontagged σ2 in SUM-AP-2.1 cells. (D) Kymograph from a representative TIRF microscopy time series showing the transient formation of diffraction-limited coated pits containing AP-2 fluorescently tagged with σ2-eGFP. (E) Histograms showing the results from the flow cytometry endocytosis assay of CD8 chimeras YAAL, EAALL, and FNPAY, comparing parental SUM159 (WT) with SUM-AP-2.1 cells. The bars represent the average ± SD from three independent experiments, each carried out in triplicate using ∼10,000 cells/measurement. Differences between WT and edited cells were statistically significant for YAAL (p < 0.01) and EAAALL (p < 0.005) but not FANPAY (p = 0.25). The statistical analysis was performed using paired Student’s t test by comparing three independent experiments.
We compared the endocytic capacity of the parental population of SUM159 cells with the clonal SUM-AP-2.1 cell line using CD8 chimeras that monitor the efficiency of clathrin-mediated endocytosis (Kozik et al., 2010). The CD8 chimeras contained the YAAL, EAAALL, or FANPAY endocytic motif in their cytosolic tails. Using flow cytometry (see Materials and Methods), we found a small decrease (with respect to wild-type cells) in the uptake of CD8 chimeras bearing the YAAL or EAAALL endocytic motifs but no significant effect on the uptake of the CD8 chimera with FANPAY (Figure 1E).
Coated-pit initiation in gene-edited SUM-AP-2.1 cells
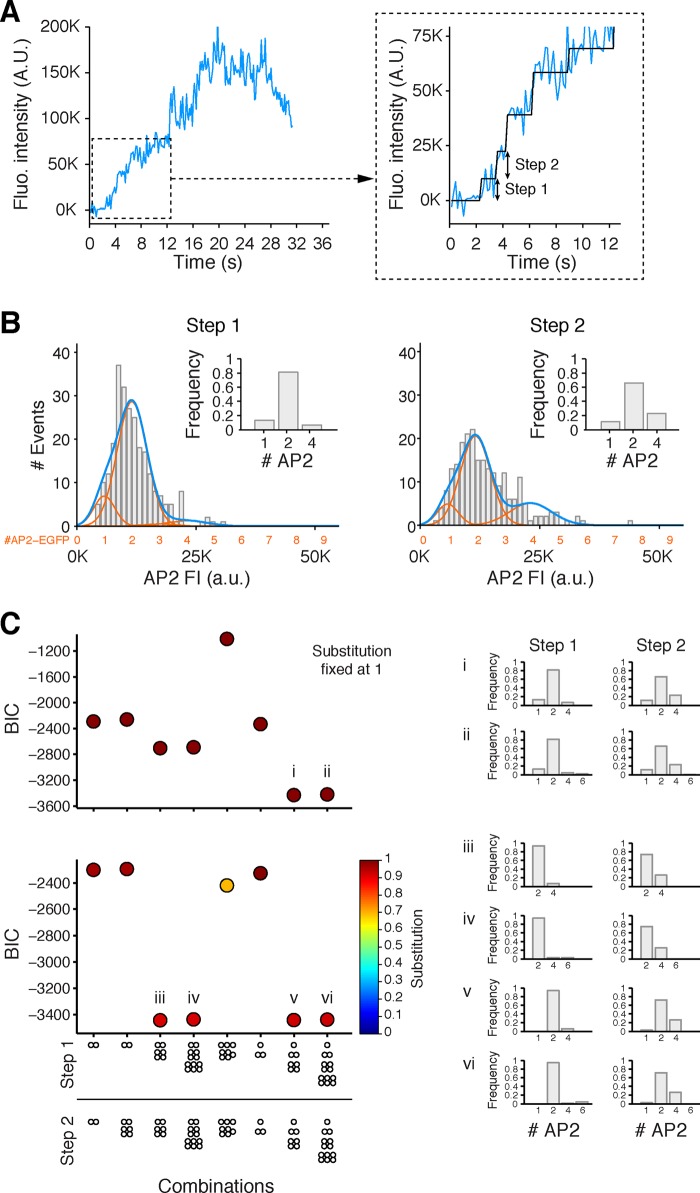
In our previous analysis of coated-pit dynamics (Cocucci et al., 2012), we found that the initial detectable molecular event was generally the appearance of one clathrin triskelion anchored to the membrane by two AP-2 complexes, which in turn depended on phosphatidylinositol 4,5-bisphosphate (PI-4,5-P2) for membrane localization (Boucrot et al., 2006; Zoncu et al., 2007; Cocucci et al., 2012). Clathrin connecting two such transiently held AP-2 complexes increased their membrane residence lifetime enough to allow capture of further copies of both components and hence to nucleate, continuing assembly (Cocucci et al., 2012). This conclusion came originally from a statistical model that took into account the relative contributions of untagged and tagged molecules in BSC1 cells ectopically expressing chimeric σ2-eGFP of AP-2 along with the endogenous, untagged protein. The gene-edited SUM-AP-2.1 cells allowed us to confirm this result in a second cell type but without the need to account for the presence of untagged molecules. As before (Cocucci et al., 2012), we used single-molecule TIRF to track the arrival of AP-2 to initiating pits. In 253 traces from three cells, the first detectable events during coated-pit initiation were two consecutive, stepwise increases in AP-2 fluorescence intensity (Figure 2A) with average dwell times of 2.9 and 2.3 s, respectively. The distribution of fluorescence intensity increments for both steps is shown in Figure 2B. Assuming full replacement of σ2 by σ2-eGFP (equivalent to a substitution fixed at 1), a search for the recruitment model with the lowest Bayesian information criterion (BIC) score (Burnham and Anderson, 2002; i.e., the model that best fit the experimental observations) yielded two AP-2 complexes per step in ∼80 and ∼70% of the first and second steps, respectively (insets in Figure 2, B and C, top, and model i). The model yielded preferential arrival of just one AP-2 complex in only 15 and 11% of the first and second steps, respectively, and of four AP-2 complexes in ∼6 and ∼20%.
FIGURE 2:
Recruitment of AP-2 during the initiation phase of coated-pit formation. (A) Representative example of a fluorescence intensity tracing of AP-2 (σ2-eGFP) from a time series obtained from SUM-AP-2.1 imaged by TIRF microscopy. The tracing corresponds to the formation of a coated pit containing AP-2 tagged by σ2-eGFP; the time series was acquired every 150 ms with an exposure of 60 ms/frame. The inset shows the fitted steps and highlights the first and second steps. (B) Histogram of the fluorescence intensities associated with the first and second steps (gray). The best fit (dark blue) corresponds to the added contributions (orange) of one, two, and so on σ2-eGFP molecules. The data from three cells correspond to 253 first and 224 second steps detected during the initiation of 253 independent coated pits. The combined dwell time for both steps was 2.6 ± 1.9 s (mean ± SD). (C) Selection of the best model describing the recruitment of AP-2 to the plasma membrane during the initiation phase of coated-pit formation. The data show the results from the process used to identify the best combination of simultaneous recruitment of AP-2 complexes fitting the experimental data for the first and second steps shown in B. The best models were identified following the procedure described in Cocucci et al. (2012) based on the BIC, where lower values indicate a better fit. Top, results obtained assuming that all AP-2s were tagged with σ2-eGFP (substitution fixed at 1); bottom, results obtained when the algorithm was allowed to search for the optimal solution, including optimization in the extent of substitution of endogenous σ2 by σ2-eGFP. Both approaches converged to similar results, in agreement with the preferential recruitment of two AP-2s during each of the steps. Right, arrival of AP-2 to the first and second steps of the models highlighted on the left with the lowest (best) BIC score. The histograms show the frequency distribution of AP-2s recruited in the initial steps.
We validated the recruitment model with an independent search that included exploration for partial replacement of σ2 by the σ2-eGFP or incomplete maturation of a fluorescent eGFP (Figure 2C, bottom, and associated models). The models iii and iv with the lowest BIC scores (<3400) converged to ∼93% substitution of endogenous AP-2 with AP-2-eGFP and a very strong preference for two AP-2 complexes (>90 and ∼80% during the first and second steps, respectively). Recruitment of 2 AP-2 complexes is thus a favored event during coated-pit initiation in cells whether they are expressing only fluorescently tagged AP-2 (this study) or a mixture of native AP-2 and fluorescently tagged AP-2 (Cocucci et al., 2012).
Imaging endocytic coated pits across the entire plasma membrane surface of SUM-AP-2.1 cells
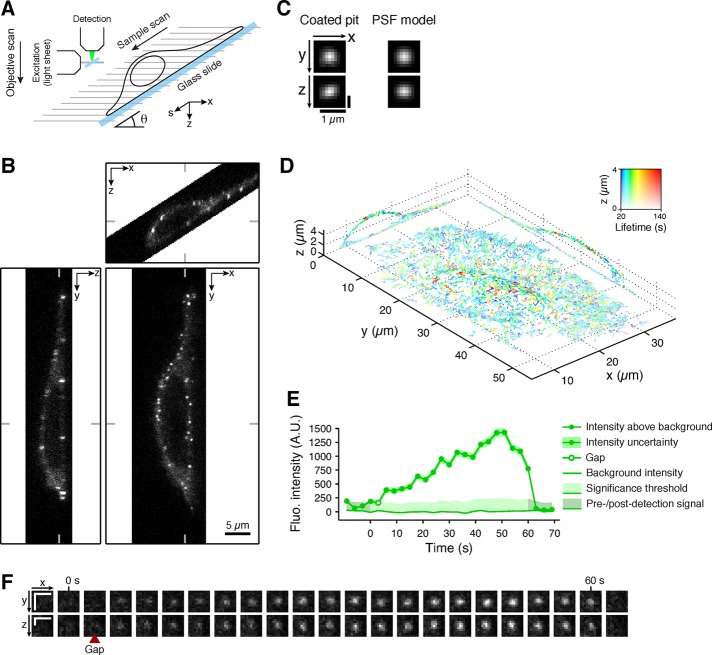
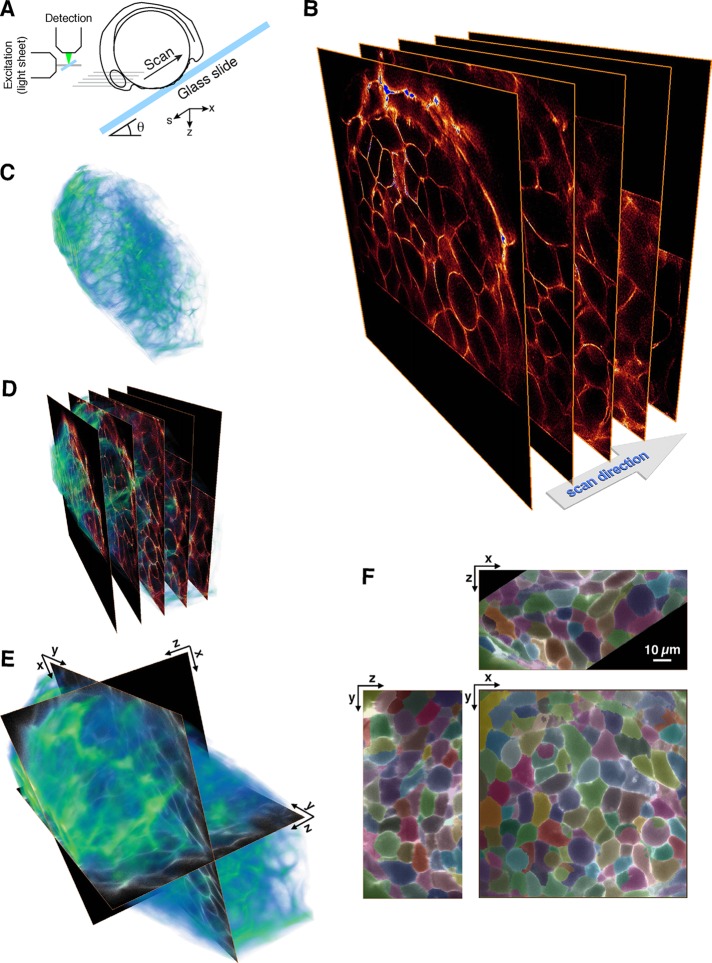
A limitation in all previous studies of coated-pit dynamics has been an effective restriction to a single cell surface (either free or attached) due to effects of bleaching and phototoxicity. The LLSM (Chen et al., 2014; Figure 3A) reduces these effects sufficiently that we can now study coated-pit dynamics or other cell biological processes throughout the cell for extended time periods. As an illustration, Supplemental Movie SM 1 shows the substantial decrease in photobleaching observed when using LLSM by comparing 3D time series obtained using spinning-disk confocal microscopy or LLSM of two cells expressing a mitochondrial marker. We followed recruitment of fluorescently tagged AP-2 over the entire plasma membrane surface of gene-edited SUM AP-2.1 cells in interphase for time periods of up to 450 s. We find no differences in the mean lifetimes or maximum intensities of coated pits assembling on the top and bottom cell surfaces, allowing us to extend the conclusions drawn from TIRF microscopy (Saffarian and Kirchhausen, 2008; Saffarian et al., 2009; Cocucci et al., 2012; Aguet et al., 2013; Merrifield and Kaksonen, 2014) and spinning-disk confocal microscopy (Ehrlich et al., 2004; Kural et al., 2015) to pit dynamics over the entire plasma membrane. For this analysis, we extended previously applied two-dimensional (2D) detection and tracking algorithms (Aguet et al., 2013) to three dimensions and showed that we can follow the trajectories of most diffraction-limited coated pits and vesicles in the imaged cell volume during an observation time much longer than their mean lifetime from initiation to uncoating.
FIGURE 3:
Three-dimensional tracking of all coated pits at the plasma membrane of cells imaged using LLSM. (A) Schematic representation of the LLSM imaging experimental setup. (B) Example of orthogonal optical sections obtained using LLSM through the approximate center of a gene-edited SUM-AP-2.1 cell expressing σ2-eGFP; raw frames obtained after deskewing the data set, corresponding to a single time point from a time series. (C) Fluorescence intensity of a single diffraction-limited spot corresponding to an AP-2-containing coated pit and its 3D PSF model used for detection (see Materials and Methods). (D) 3D trajectories color-coded for lifetime of all diffraction-limited fluorescent structures containing AP-2-eGFP tracked from a time series of the cell shown in B and identified by using automated 3D detection (see Materials and Methods and Supplemental Movie SM 2a). (E) Representative example of a fluorescence intensity trace of a coated pit tracked in D and the fluorescence immediately next to it (background). Uncertainties are shown as 95% confidence intervals. The small gap (white circle) in the intensity tracing indicates failure by the detection algorithm to detect the signal due to insufficient signal-to-noise ratio. (F) Orthogonal cross-sections of individual volume frames for all of the time points corresponding to the coated pit analyzed in E. Scale bars, 1 μm.
The data sets contained 90–100 _z_-stacks, composed of ∼50 sequential optical sections, each acquired with ∼40-ms exposure time and spaced ∼250 nm apart along the detection axis. Representative orthogonal sections (Figure 3B) from an image volume acquired at a single time point illustrate the distribution of AP-2 spots as restricted to the cell surface, as expected (Robinson, 1987; Ahle et al., 1988; Ehrlich et al., 2004).
The diffraction-limited fluorescent AP-2 spots (representative example shown in Figure 3C) had a point-spread function (PSF) with an invariant Gaussian profile, consistent with the 3D quasi-isotropic properties of the LLSM (Chen et al., 2014; Gao et al., 2014). We could therefore use a 3D Gaussian model to generalize to three dimensions the automated spot detection algorithm developed previously for 2D detection (Aguet et al., 2013). The algorithm (described in Materials and Methods) uses a computationally efficient filtering step to identify locations with statistically significant signal in volumetric data, enabling rapid detection of coated pits in the large LLSM data sets (∼2 GB/channel for a movie with 100 frames). Implementation of the 3D detection algorithm in a previously described software framework (Jaqaman et al., 2008; Aguet et al., 2013) enabled us to detect 3D trajectories of all AP-2–containing endocytic coated pits and vesicles formed asynchronously on both the top and bottom surfaces of the SUM-AP-2.1 cells first described in Kural et al. (2015). The example in Figure 3D shows the 3D trajectories of bona fide coated pits and vesicles color-coded for their lifetimes. The fluorescence intensity trace for a single coated pit, including confidence intervals derived from background noise, is shown in Figure 3E, and the cross-sections of individual volume frames obtained from the same pit are shown in Figure 3F. Supplemental Movie SM 2a (related to Figure 3D) shows the 3D time series, in which all of the coated-pit tracings were color-coded for their fluorescence intensity and then overlaid on the cell volume.
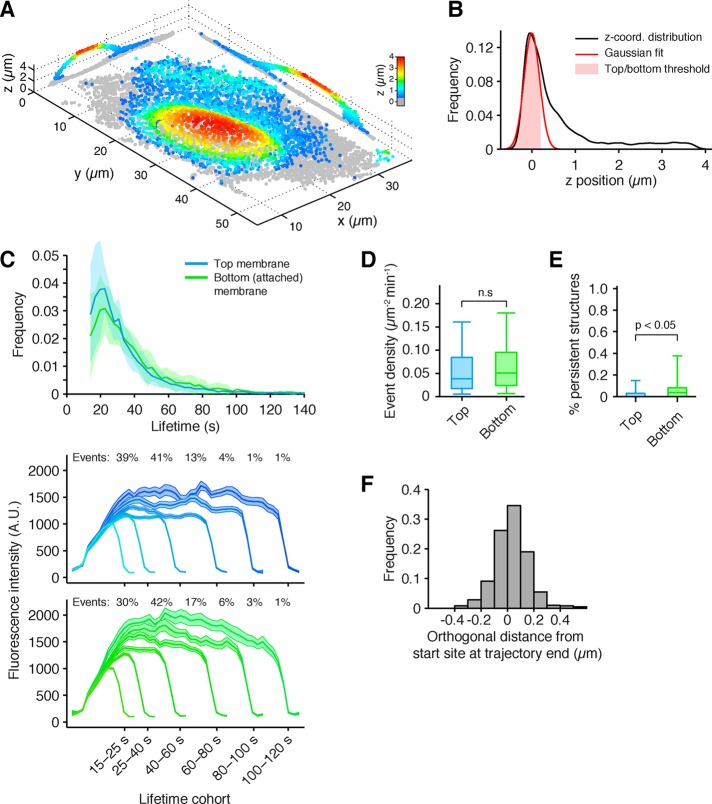
The improved 3D detection algorithm allowed us to determine the mean location of each AP-2 spot as it formed on either surface of each analyzed cell. The example in Figure 4A shows the location of AP-2 spots in the SUM-AP-2.1 cell presented in Figure 3D color-coded for their relative _z_-position with respect to the surface of the glass coverslip. Their locations were determined from the centroid position of the fluorescence spot; those close to the glass defined the baseline corresponding to the bottom surface (Figure 4A, gray spots); the remaining AP-2 spots were sorted into the upper surface based on their distance from this baseline (Figure 4A, other colors). The location of the bottom surface was defined by thresholding the position of the AP-2 spots with the mean plus 1 SD of a Gaussian distribution fitted to the lowest maximum (closest to the glass) of the distribution of all _z_-positions of AP-2 spots in each analyzed cell (Figure 4B). This procedure allowed us to compare the pit dynamics on both surfaces of any given cell. The ensemble analysis (Figure 4C) performed for >250,000 AP-2 containing structures at both surfaces from 45 cells showed ∼33,000 bona fide nonabortive coated pits and vesicles with similar distributions of lifetimes, indicating similar assembly dynamics, and equivalent maximum fluorescence intensities, indicating similar coated vesicle sizes (Ehrlich et al., 2004). The analysis also showed a similar surface density of pits (Figure 4D) and the presence of a small number of persistent AP-2 spots (likely coated plaques) on the bottom surface of the cells (Figure 4E). The density of persistent objects increased with the duration of plating (unpublished data), as often observed with other adherent cells studied in vitro (Ehrlich et al., 2004; Cocucci et al., 2012, 2014). Rare persistent AP-2 objects (∼0.1% of events) were also detected on the top surface (Figure 4E); the coat geometry of such objects remains to be determined. Similar results were obtained using SUM AP-2.2 and SUM AP-2.3 cells gene edited in both alleles to express σ2-eGFP and μ2-eGFP, respectively (Supplemental Figures S1 and S2).
FIGURE 4:
Dynamics of coated-pit and coated-vesicle formation throughout the entire surface of the cell. (A) Example showing the average position over time of all AP-2–containing endocytic coated pits and vesicles detected in a gene-edited SUM159-AP-2.1 cells expressing σ2-eGFP and imaged with LLSM.1. The coated pits and vesicles located at the dorsal (free) surface are color coded (rainbow) according to their distance from the glass coverslip. Those at the ventral (attached) surface are shown as gray dots. The orthogonal views correspond to optical sections through the center of the cell. (B) Distribution of the _z_-position of all detected coated pits and vesicles; the pits and vesicles associated with the ventral membrane were automatically detected by fitting a Gaussian model to the distribution of _z_-positions (see Materials and Methods). (C–E) Automated analysis of coated-pit and coated-vesicle formation obtained from 45 cells and ∼250,000 AP-2 traces. The results from the analysis exclude abortive coated pits (lifetime <15 s) and highlight the lifetime distribution from the 45 cells (mean ± SD) and average intensity of all valid coated structures (∼31,000) detected in the top (dorsal, free; ∼18,000) and bottom (ventral, attached; ∼13,000) surfaces (C), their spatial density (D), and the density of persistent structures (E). The intensities are shown as median ± SE; box plots show median, 25th, and 75th percentiles and outermost data points. The p values are from a permutation test for medians. (F) Distribution of the orthogonal distance relative to the closest cell membrane, determined as the displacement between the beginning and end of the trajectory for each AP-2–containing coated pit/vesicle in the 11 cells analyzed (see Materials and Methods). Owing to uncertainty in the measurement of the membrane and coated vesicle positions, vesicle positions are in some instances measured as outside the cell boundary, resulting in negative distances.
We took advantage of the high spatial precision of the LLSM data to determine the distance from the plasma membrane of all coated vesicles immediately before uncoating. The measurement (∼35 ± 130 nm; Figure 4F) represents the orthogonal displacement of the centroid of a given AP-2 spot from the membrane between the beginning and the end of its trajectory (marked by loss of fluorescence signal and hence used as a proxy for uncoating). The SD reflects uncertainty in pit and membrane positions, the latter determined by segmentation (see Materials and Methods). These measurements provide direct experimental evidence for short-range displacement of the coated vesicle away from the plasma membrane before the start of the uncoating reaction, as proposed previously (Ehrlich et al., 2004).
Coated-pit dynamics during cell division
Before the advent of LLSM, we used spinning-disk confocal fluorescence microscopy to trace the formation of coated pits and vesicles during mitosis in naturally dividing cells (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013). From these results, we proposed uniform pit assembly dynamics during all stages of cell division (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013). The time series were restricted, however, to brief single-plane data sets acquired from the bottom surface, as it was not possible to obtain 3D sets from the top surface due to extensive photobleaching and phototoxicity. Taking advantage of LLSM, we now traced the formation of most AP-2–coated pits and vesicles across the entire plasma membrane surface of a naturally dividing cell (Figure 5). During mitosis, clathrin-coated pits continue to form, as we found previously (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013).
FIGURE 5:
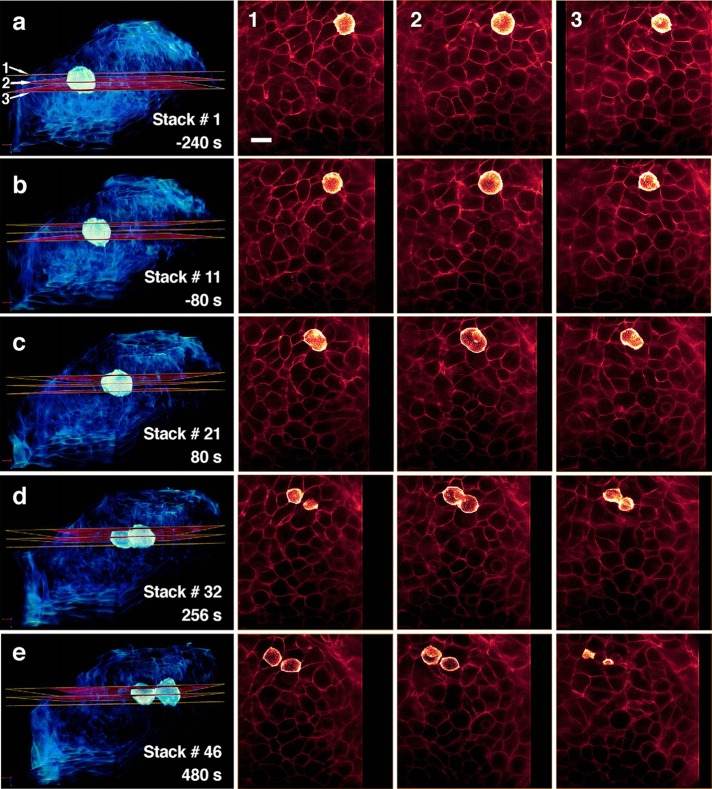
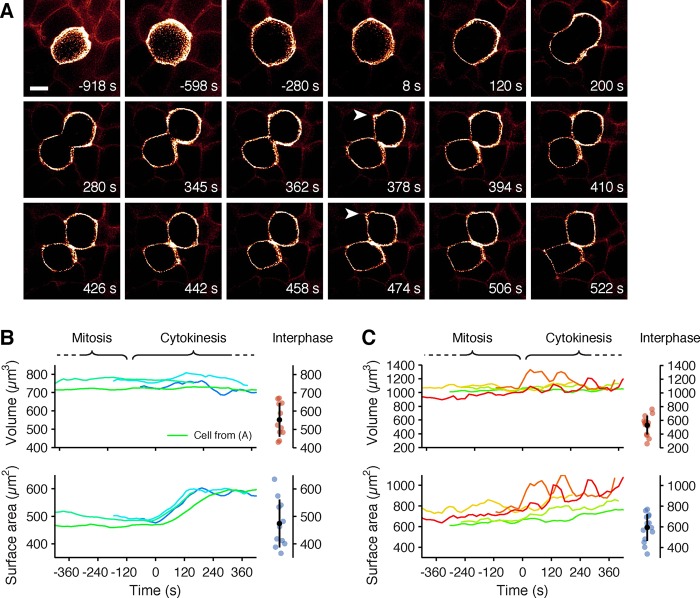
Plasma membrane and volume dynamics of SUM-AP-2.1 cells during cell division. (A) Examples of orthogonal sections from different time points of six consecutive time series obtained in three dimensions with LLSM.1 during cell division of a gene-edited SUM-AP-2.1 cell (Supplemental Movies SM 2b and 2c). Arrowheads highlight examples of transient blebs typically observed at the onset of anaphase (Boucrot and Kirchhausen, 2007). (B) Example of another gene-edited SUM-AP-2.1 cell undergoing cell division imaged using LLSM.1 (Supplemental Movies SM 2d and 2e). (C) Example of a third cell undergoing cell division imaged using LLSM.2. This set of images highlights a common behavior by which the cell interior rotates as it undergoes mitosis. The first three columns show deconvolved 3D projections of a mitotic cell in coordinates orthogonal to the coverslip. The fourth column corresponds to the center optical section of the raw data oriented parallel to the coverslip. (D) Plots corresponding to the values of cell volume, surface area, and event density for the appearance of AP-2 spots at the plasma membrane as determined from multiple time series of 2.5–2.8 min in duration for eight different cells undergoing cell division. The volume and surface area of cells during cytokinesis correspond to the added value of the two offspring cells. The event density includes all objects with lifetimes of 10 s or longer that appeared and disappeared during the duration of the time series. The intervals i–vi correspond to the time points for the cell depicted in A. Images from two of the remaining cells are shown in C and B. Dots correspond to additional data from different independent cells obtained from a single time series acquired during mitosis or interphase. (E) Lifetime distributions of all AP-2–containing coated pits and vesicles in the cell from A detected during each of the recorded intervals.
Metaphase SUM-AP-2.1 cells, identified by their spherical appearance, were imaged in three dimensions during the ensuing stages of cell division. We generated consecutive imaging bursts of 2.4- to 3-min duration, with 3D stacks at 2.4- to 3.0-s intervals, each composed of 50–60 planes spaced 500 nm apart. This imaging protocol provided the required temporal resolution (∼3 s; Ehrlich et al., 2004; Aguet et al., 2013) and spatial resolution (∼230 nm in xy and ∼600 nm in z; Chen et al., 2014) to resolve and track each assembling pit. The snapshots in Figure 5, A–C (see also Supplemental Movies SM 2b–2f), show raw images from single optical sections of the full volumetric data for three different cells, each at three different time points. Figure 5C includes projected orthogonal views (see Supplemental Movie SM 2f). These figures illustrate the presence of AP-2 spots on the plasma membrane throughout mitosis and cytokinesis. The complete data set used for analysis included results from eight cells followed during their division and from 23 cells imaged for a single ∼3-min interval during either metaphase or interphase. The results obtained for objects with lifetimes >10 s are shown in Figure 5D, bottom panel, and for objects with lifetimes >25 s in Supplemental Figure S3. Analysis of pit dynamics showed invariant surface density of endocytic coated pits and vesicles in cells imaged during interphase and during late phases of cytokinesis but a transiently lower density in cells imaged during metaphase. In four cases in which we followed the activity of pit dynamics for the same dividing cell, recovery of the original surface density coincided with cell reattachment to the substrate and spreading, whereas in one case, the density remained low in the daughter cells, which failed to fully reattach and spread (cell from Figure 5B and Supplemental Movie SM 2e). In all cases, however, the distribution of AP-2 lifetimes was unaffected throughout cell division (selected example shown in Figure 5E for cell from Figure 5A).
Surface area and volume of dividing cells grown in culture
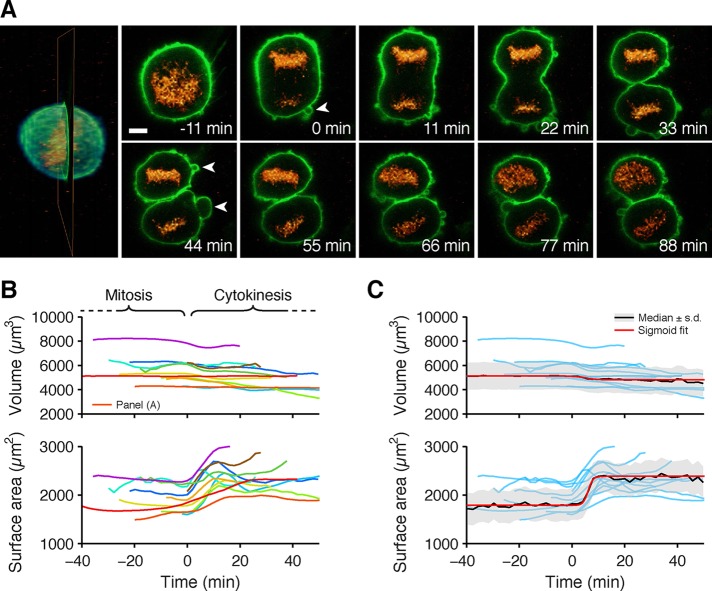
From the same 3D data sets used to trace AP-2 events, we determined the location of the plasma membrane as defined by the boundary between soluble cytosolic fluorescent AP-2 and the surrounding extracellular medium lacking AP-2 (see Materials and Methods). The cell surface area and the corresponding cell volume were then calculated from the location of the plasma membrane as the cell progressed through division (Figure 5D). As shown earlier (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013), the surface area of a typical cell was smallest during mitosis (less in individual prometaphase than in metaphase cells) and was relatively constant during the last ∼20 min of mitosis, including metaphase, anaphase, and telophase (tracking of selected cells). The total surface of the two daughter cells increased rapidly during the transition from telophase to early stages of cytokinesis (ingression of the membrane furrow along the equator), after which the surface area remained relatively constant for at least 30 min, until abscission. We obtained similar results with 11 BSC1 cells, visualizing the plasma membrane directly by ectopic expression of eGFP fused at its C-terminus with the plasma membrane–sorting motif CAAX (Figure 6, A and B, and Supplemental Movies SM 3a and 3b) used as a way to more accurately delineate the cell surface. The rapid increase in surface area was accompanied by plasma membrane blebbing (examples highlighted by arrows in Figures 5, A and B, and 6A and Supplemental Movie SM 3b), as previously noted for adherent BSC1 and HeLa cells and nonadherent Jurkat and Sf9 cells (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013).
FIGURE 6:
Plasma membrane and volume dynamics of BSC1 cells during cell division. BSC1 cells stably expressing eGFP-CAAX (green) to label the plasma membrane and H2b-mCherry (orange) to label the chromosomes were imaged using LLSM.1 in three dimensions during cell division. (A) Example of an image (left) rendered in 3D, highlighting the optical section used to show selected examples (right) obtained from the time series acquired during mitosis. Examples show plasma membrane blebs (arrowheads) appearing during anaphase and continuing through cytokinesis. Scale bar, 5 μm. (B) Plots correspond to the values of cell volume and surface area determined for 11 cells undergoing cell division. The volume and surface area of cells during cytokinesis correspond to the combination of the two offspring cells. Traces were smoothened using the smooth function with default parameters in MATLAB. (C) Traces from B (light blue) were normalized to their respective starting values, scaled to the median value of all the cells (black), and fitted with a sigmoid function (red). During cytokinesis, 50% of surface area was recovered in ∼6 ± 0.6 min.
Our data sets for individual cells undergoing division do not include the corresponding interphase cell just before mitosis due to lack of a cellular marker that could highlight the onset of the interphase-to-prometaphase transition. Because we could determine the surface area of only interphase cells of unknown longevity, we measured a range of sizes representing cells imaged at different stages of growth during G1 and S phase and then used this range for comparison with the surface areas of the cells traced during cell division (Figure 5D). As expected, the data showed that the surface area decreased as cells entered mitosis and recovered rapidly as they exited. The recovery was complete before abscission.
From the same 3D LLSM data sets used for the surface area calculations, we determined the volume of the SUM-AP-2.1 cells (analyzed using the AP-2 signal) and BSC1 cells (analyzed using the surface marker) as they transitioned from late stages of mitosis through cytokinesis. The volume of individual metaphase cells was slightly larger than that of prometaphase cells and decreased slightly or remained relatively constant afterward, as determined by the combined volume of the two daughter cells (Figures 5C and 6B).
Surface area and volume of dividing cells in the developing eye of a zebrafish embryo
Because cells within a living tissue are exposed to force and space constraints supplied by neighboring cells, it is possible that the changes in area and volume of dividing cells just described in culture are different in living tissues. We used LLSM to investigate these properties. We imaged the developing eye and the spinal tissue of zebrafish embryos, in which the cells undergo active cell division ∼17 h postfertilization. As with the BSC1 cells, we directly visualized the plasma membrane of cells, in this case marked by fluorescent citrine containing the palmitoylation and myristoylation sequence motifs from lyn kinase (Mosaliganti et al., 2012; Swinburne et al., 2015) expressed as a transgene in all cells. The _z_-stacks of the 3D time series, acquired for periods of 60–120 min, were obtained by translating the sample stage; they comprised ∼250 optical sections spaced at 400 nm along the s-axis, acquired with ∼40-ms exposures per frame. Figure 7, A–E, shows a schematic diagram of the imaging setup, highlighting the relative orientation of the zebrafish embryo and the eye, a volumetric representation of a 3D capture, and a display of selected planes. The associated movies (Supplemental Movies SM 4a and 4b) demonstrate the remarkable aggregated 3D motility of the cells during the imaging period. All cells in the time series were uniquely identified with Automated Cell Morphology Extractor (ACME) software, which reconstructs the cellular boundary and segments out cells from 3D membrane images in dense tissues (Mosaliganti et al., 2012; see Materials and Methods). An example for a single time point within the tissue volume of the eye is shown in Figure 7F. Supplemental Movie SM 5 illustrates two cells undergoing division located visually and whose segmented cell boundaries were verified manually. We used a custom MATLAB routine to track cells as they divided and then used their cell boundaries, determined by ACME, to calculate the variation of surface area and volume with time. Figure 8 shows a dividing cell within a representative volumetric view of the eye and three planes for five different time points. As in the aforementioned measurements of cultured cells, the area of mitotic cells in the eye and spine increased at the onset of cytokinesis and then was relatively constant during the remaining phases of cytokinesis (Figure 9). Membrane blebbing similarly accompanied the rapid deposition of new membrane (Figure 9A, arrows for the eye, and data not shown for the spine). The combined volume of the two daughter cells barely decreased during cytokinesis and was similar to that of the mitotic cell before birth (Figure 9B). We obtained similar results with five dividing cells in the spinal tissue of zebrafish embryos from the same citrine-tagged line (two cells) and from wild-type zebrafish strain AB (three cells) in which the citrine tag was introduced into oocytes by injecting mRNA encoding fluorescent citrine fused to the palmitoylation and myristoylation sequence motifs (Figure 9C).
FIGURE 7:
Three-dimensional visualization of single cells within the multicellular developing eye of a zebrafish embryo using LLSM. (A) Schematic representation of the optical setup and the position of the zebrafish embryo mounted in the LLSM.2. Each image stack was acquired during a 10-s period followed by a 6-s pause and was composed of 251 planes obtained by scanning the embryo along the s-axis (sample scan mode) with consecutive lattice light sheets placed at 400-nm intervals. (B–D) Different views obtained at a single time point from the same volume (∼80 × 80 × 100 μm) of the developing eye of zebrafish embryos expressing fluorescent citrine targeted to the plasma membrane imaged 17 h postfertilization; the images were deconvolved in order to facilitate their visualization. The examples in B and C show selected optical sections separated by ∼10 μm (50 planes); the fluorescence outline of the plasma membrane is indicated in orange. The images in C and D were rendered at 50% transparency. (E) Relationship between the full 3D image from a single raw (nondeconvolved) time point of the time series and its three orthogonal optical sections (F) approximately centered in the imaged volume. (F) Orthogonal sections showing the outcome of the automated 3D segmentation of the plasma membrane for the cells within the imaged volume of the developing zebrafish eye. The cells in the volume were color coded randomly to illustrate the results from the membrane delineation (see Materials and Methods).
FIGURE 8:
Automated tracking of a dividing cell in the developing eye of a zebrafish embryo visualized using LLSM. Images from LLSM.2 showing the appearance of a representative cell within the zebrafish embryo undergoing cell division obtained from the 3D time series depicted in Figure 7. The deconvolved images in the left column were acquired at the specified time points and highlight the location of three consecutive optical sections from the image stack intersecting the dividing cell. Deconvolved versions of these sections are shown in the three rightmost columns. The fluorescence signals generated by the cells surrounding the mitotic cell are shown at 20% of their intensity, and the volumetric image is displayed with 50% volume transparency. Scale bar, 10 μm.
FIGURE 9:
Membrane and volume dynamics of dividing cells in the developing eye of zebrafish embryos. (A) Representative deconvolved images corresponding to the central cross-section obtained using LLSM.2 from a 3D time series of a dividing cell within the developing eye of a zebrafish embryo expressing fluorescent citrine targeted to the plasma membrane. Selected examples of membrane blebs appearing during early stages of cytokinesis are highlighted with arrowheads. Scale bar, 5 μm. (B) Cell volume and surface area corresponding to four dividing eye cells (time courses) and 11 cells in interphase (dots) imaged using LLSM.2. Values obtained during cytokinesis correspond to the sum of the values from the two offspring cells. All traces were aligned with the onset of cytokinesis, defined as t = 0 s. (C) Cell volume and surface area for five dividing spinal cells (time courses) and 15 cells in interphase (dots) imaged using LLSM.2. Values obtained during cytokinesis correspond to the sum of the values from the two offspring cells. All traces were aligned with the onset of cytokinesis, defined as t = 0 s.
The distributions of surface area and volume of the round (i.e., metaphase) cells were relatively narrow, but the corresponding values for 11 nonspherical (e.g., interphase) cells randomly selected from the same imaging views of the eye were relatively broad and centered on a smaller mean than those of the mitotic cells (Figure 9B). We interpret these comparisons to reflect that in the rapidly developing eye, the imaged interphase cells are a “sampling” of cells biased toward the most abundant population representing early interphase, when the cells are still growing.
DISCUSSION
The experiments we report here illustrate the quantitative application of three new and powerful features of lattice light-sheet microscopy. The first is time resolution of ∼2 s across an entire cell for repeated periods of several minutes with low photodamage, high signal-to-noise ratio, and excellent 3D resolution. We used this property to determine the assembly dynamics of most endocytic coated pits and vesicles that form at the plasma membrane of cells during interphase and cell division. The second is determination of changes in the area and volume of single cultured cells over different stages of the cell cycle. The third is extension of area and volume measurements to cells within intact, living tissues. The developing eye of zebrafish embryos is a particularly useful model system in this regard due to its relatively high frequency of cell division. Instrumental to these studies was the implementation of new analytical tools for the automated identification and 3D tracking over time of the fluorescence signal generated by diffraction-limited objects.
The earliest studies of coated-pit dynamics in living cells relied either on spinning-disk confocal microscopy to distinguish top and bottom surfaces of a cell (Ehrlich et al., 2004; Boucrot and Kirchhausen, 2008; Kural et al., 2015) or TIRF microscopy to achieve high signal-to-noise ratio on the adherent surface only (Merrifield et al., 2002, 2005; Merrifield and Kaksonen, 2014; Saffarian and Kirchhausen, 2008; Saffarian et al., 2009; Aguet et al., 2013; Cocucci et al., 2014). The LLSM offers the low background and reduced photobleaching of TIRF in three dimensions rather than two. In addition, the speed and high axial resolution of LLSM permit many more optical sections to be acquired over the thickness of the cell, permitting cells to be studied over their entire dorsal surface. These include cells well suited for complete replacement of endogenous proteins by gene editing, such as those of the largely diploid human SUM159 line. Expression of a protein bearing a fluorescent tag at physiological levels and in the absence of any untagged protein (Doyon et al., 2011; Cocucci et al., 2012, 2014; Grassart et al., 2014; Hong et al., 2015; Kural et al., 2015) circumvents many of the confounding factors in previous efforts to count the number of molecules that participate in limiting events such as initiation (Cocucci et al., 2012) or termination (Cocucci et al., 2014; Grassart et al., 2014) of a clathrin-coated pit. We thus reinforced our conclusion from earlier work that the predominant molecular event for initiating coated-pit assembly is arrival at the site of the future pit of a clathrin triskelion captured at the membrane by two AP-2 complexes (Cocucci et al., 2012). Cross-linking (by clathrin) of two AP-2 complexes extends the membrane residence lifetime of AP-2, initially localized by association with PI-4,5-P2 head groups, to increase the likelihood of capturing an additional, AP-2-bound clathrin (Cocucci et al., 2012). We now further showed that the dynamics and size distribution of coated pits are uniform over the entire cell surface of the SUM 159 cells and that long-lived “coated plaques” accumulate only on the adherent cell surface and only after extended periods after initial attachment to the coverslip (Kirchhausen, 2009; Saffarian et al., 2009; Grove et al., 2014). This property of a stationary cell contrasts with the uneven distribution of coated pits and vesicles at the leading edge of a migrating cell. These structures are notably absent on the ventral surface near the leading edge of lateral membrane protrusions (Kural et al., 2015). Finally, we used the high 3D spatial resolution afforded by LLSM to measure the mean separation from the plasma membrane of budded coated vesicles at the time uncoating begins.
We extended our studies to dividing cells in an effort to resolve a debate about the persistence of clathrin-mediated endocytosis during mitosis (Boucrot and Kirchhausen, 2007; Fielding et al., 2012; Tacheva-Grigorova et al., 2013; Kaur et al., 2014). We showed in work using spinning-disk confocal microscopy that coated-pit assembly continues during mitosis, even though transferrin uptake ceases (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013). We further showed that cessation of transferrin uptake mainly comes from loss of transferrin receptors at the cell surface (Boucrot and Kirchhausen, 2007), later confirmed using mass spectrometry (Cocucci et al., 2012; Ozlu et al., 2014), due to cessation of exocytosis rather than from absence of any clathrin-mediated endocytic activity (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013).
Better measurements of surface area have now given us more accurate numbers for this parameter and the density of coated-pit activity. We confirm our earlier interpretation that the contribution to decreased overall transferrin uptake is primarily due to the decreased surface area over which it occurs, and in addition we now detect during metaphase a decrease of up to 50% of overall coated-pit/vesicle density, which we could not previously have observed. The combined effect, that is, decrease in surface area and endocytic rate, is that the absolute rate of coat formation per cell normalized by surface area drops to approximately one-fourth of its late interphase level when the surface area of the cell is at a minimum (metaphase). Nevertheless, the dynamics of the residual clathrin activity remain normal. It is possible that the earlier interpretation that endocytosis ceases completely (Fielding et al., 2012; Kaur et al., 2014) was based on failure to detect this reduced but nonnegligible activity (Boucrot and Kirchhausen, 2007; Tacheva-Grigorova et al., 2013) combined with the substantial depletion of transferrin receptor at the cell surface (Boucrot and Kirchhausen, 2007; Ozlu et al., 2014).
Various factors might account for a decreased density of endocytic coated pits during metaphase through telophase. Pit initiation depends in part on the concentration of PI-4,5-P2 in the plasma membrane, but we have no information about the potential variation of this component during division of SUM or BSC-1 cells. The surface concentration of many proteins, including the transferrin receptor, decreases during mitosis (Boucrot and Kirchhausen, 2007; Ozlu et al., 2014), and because cargo capture commits a coated pit to continued growth and completion (Ehrlich et al., 2004; Liu et al., 2010), a lower frequency of cargo capture could result in an increased fraction of abortive initiation events and a decrease in fully formed functional coated pits and vesicles. Increased membrane tension during mitosis (Stewart et al., 2011; Fischer-Friedrich et al., 2014) in the absence of actin dynamics is not likely to account for the decreased coated pit density, as in one previous suggestion (Kaur et al., 2014), because tension per se, together with absence of actin dynamics, does not lead to decreased initiation but instead to “frozen” assemblies (Boulant et al., 2011).
As recently described by using a fluorescence exclusion (Zlotek-Zlotkiewicz et al., 2015) or a suspended microchannel resonator approach (Son et al., 2015), depending on cell type, the cell volume increases briefly during metaphase by up to 30%, whereas the total volume of the two daughter cells is, within experimental error, equal to that of the mother cell immediately before entry into mitosis (as we concluded previously; Boucrot and Kirchhausen, 2008). A recent study (Zlotek-Zlotkiewicz et al., 2015) also showed similar cell volume estimates from the fluorescence exclusion approach and from a geometric calculation derived by fitting the maximal diameter of the circle defined by the exclusion volume or the cortical actin fluorescent signal of metaphase cells probed with Lifeact (similar to determination of the cell boundary using membrane or cytosolic fluorescent probes done here). The easier-to-quantify measurements of volume afforded by the LLSM eliminate an anomaly in our earlier work, which appeared to show a transient drop in cell volume from prometaphase to anaphase. The discrepancy in the total volume determination was due to a systematic error in the masking procedure originally used to mark the cell boundary from data acquired using spinning-disk confocal microscopy, induced by the considerable dispersion (∼1.2 μm) of the PSF along the optical _z_-axis. Instead of locating the membrane as the position with the maximal _z_-axial intensity containing the fluorescence signal generated by a membrane marker, the previous approach selected the outermost _z_-axial location containing a fluorescence signal. The resulting error artificially raised the relative position of the plasma membrane, leading to an overestimate of the calculated volume, which was particularly noticeable in regions associated with the peripheral flat regions where top and bottom surfaces are in close proximity. Reevaluation of all of the original images, using the algorithm used here, to map analytically the location of the cell membrane is consistent with a slight increase between prophase and metaphase and minimal volume change thereafter.
Despite the increase in spatial precision provided by the live-cell LLSM measurements, we are unable to account directly for potential contributions that might be provided to the surface area by subresolution features such as microvilli. We believe, however, that the presence of a large number of such membrane folds particularly during mitosis is unlikely, as they would have been detected as a relative increase in fluorescence intensity of the cell membrane marker. In the future, one way to address this question more precisely could be by using focused ion beam scanning electron microscopy to obtain high-resolution full volumetric images of cells during different stages of cell division.
We previously showed the appearance of nondeleterious blebs that rapidly appear and disappear in a time frame of seconds during the reactivation of exocytosis (Boucrot and Kirchhausen, 2007). Blebbing is at the outer surface of adherent and nonadherent mammalian cells dividing at 37°C in culture, mostly at the distal poles and away from the cleavage furrow until late stages of cytokinesis. These observations were extended here to cells dividing in situ and at room temperature in the developing eye of zebrafish embryos. The correlation of plasma membrane recovery with formation of surface blebs seems to be a general property of dividing animal cells.
Taking advantage of powerful features of full-cell imaging provided by the lattice light-sheet microscope, our study clarifies a debated point by showing that coated-pit dynamics indeed persist during cell division of mammalian cells in culture. It also shows that the volume remains relatively constant during cell division for the cell types we studied in vitro and for those in the developing zebrafish embryo. Finally, it confirms that, like in cells grown in culture, the surface area of dividing cells in tissue is modulated, reaching a minimum during mitosis and rapidly increasing during cytokinesis.
MATERIALS AND METHODS
Cell culture
Human-derived, mostly diploid SUM159 cells were grown in DMEM/F-12/GlutaMAX (10565-042; Thermo Fisher Scientific, Waltham, MA) supplemented with 5% fetal bovine serum (FBS; S11150; Atlanta Biologicals, Flowery Branch, GA), 100 U/ml penicillin and streptomycin (45000-652; VWR International, Radnor, PA), 1 μg/ml hydrocortisone (H4001; Sigma-Aldrich, St. Louis, MO), 5 μg/ml insulin (I9278; Sigma-Aldrich), and 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES; 25-060-CI; Mediatech, Manassas, VA), pH 7.4. The BSC1 monkey kidney epithelial cells stably expressing eGFP-CAAX (Boucrot and Kirchhausen, 2007) together with H2B-mCherry were generated by transfection with a plasmid encoding H2B-mCherry. Cells simultaneously expressing eGFP-CAAX and H2B-mCherry were selected for 7 d using 50 μg/ml puromycin, followed by cell sorting with FACSAria II (BD Biosciences, San Jose, CA). Cells were grown in DMEM (10569-044; Life Technologies) supplemented with 10% FBS, 100 U/ml penicillin and streptomycin, and, when required, 50 μg /ml puromycin.
Gene editing
SUM159 cells were gene edited in both alleles to replace the σ2 subunit of AP-2 with σ2 fused at its C-terminus to eGFP using a TALEN-based protocol (Sanjana et al., 2012). The resulting cell line, first described in Kural et al. (2015), is here named SUM-AP-2.1. The downstream targeting sequence, 5′ TGCTGAAACAGCTGCTGATG 3′, overlapped the σ2 TGA stop codon (antiparallel, underlined), and the upstream targeting sequence, 5′ TGGGGCTCGCCTGCCCTCAC 3′′, is located 14 nucleotides upstream (Figure 1A). The donor construct was generated using the following primers:
| σ2 up | F1 AGTGGTGCAATCTTGGCTCATTGC |
|---|---|
| R1 CATGGTGGCGACCGGTGGATCCTCCAGGGAC-TGTAGCATCAG | |
| σ2 eGFP | F2 GATCCACCGGTCGCCACCATG |
| R2 GGGGTGGGGCTCGCCTGCCCTTACTTGTACA-GCTCGTCCATGCC | |
| σ2 down | F3 GGGCAGGCGAGCCCCACC |
| R3 CCAGGTATGGTGGCACACATC |
In brief, SUM159 cells were cotransfected with 600 ng each of the upstream and downstream TALEN targeting sequences and the pCR8/GW vector containing the donor construct transfected using TransIT 2020 Transfection Reagent (Mirus Bio, Madison, WI) into 1.5 × 105 SUM159 cells plated the day before in six-well plates. A monoclonal cell line gene edited in both alleles for σ2-eGFP was obtained by flow cytometry single-cell sorting using a FACSAria 2-SORP (BD Biosciences) equipped with a 300-mW, 488-nm laser and a 70-μm nozzle. Clone D8 (SUM-AP-2.1) was identified by PCR amplification from purified genomic DNA using GoTaq Polymerase (Promega, Madison, WI) with forward primer 5′ TGAGGTCTGTGTCCCAGCTC 3′ and reverse primer 5′ GGTTACTCGGGACACACACG 3′. These primers map a genomic region containing the σ2 stop codon; amplified wild-type σ2 generates a 426–base pair product, and insertion of eGFP results in a 1151–base pair product. Expression of σ2-eGFP instead of σ2 was confirmed by SDS–PAGE and Western blot analysis.
SUM AP-2.2 cell line (expressing the σ2 subunit of AP-2 fused at its C-terminus to eGFP instead of σ2) and SUM AP-2.3 cell line (expressing the μ2 subunit of AP-2 with eGFP inserted between residues 236 and 237 of μ2) gene edited in both alleles were obtained by using a clustered regularly interspaced short palindromic repeats/Cas9 protocol as previously described (Chou et al., 2016). A free PCR strategy (Ran et al., 2013) was used to generate the small guide RNAs with target sequences specific for AP2-σ2 or AP2-μ2. A DNA fragment containing the U6 promoter was generated by PCR with forward primer 5′ GCCGGTACCTGAGGGCCTATTTCCC 3′ and reverse primer 5′ ACCTCTAGAAAAAAAGCACCGACTCGGTGCCACTTTTTCAAGTTGATAACGGACTAGCCTTATTTTAACTTGCTATTTCTAGCTCTAAAACNNNNNNNNNNNNNNNNNNNNCGGTGTTTCGTCCTTTCCACAAG 3′, with the underlined nucleotides representing the complimentary sequences of the target sequences for σ2 and μ2, GCTACAGTCCCTGGAGGGGC and GATTGCTTCCCGCTGCAAGC, respectively.
Cloning into the pcDNA3.3 vector a genomic DNA fragment containing the sequence for eGFP generated the donor constructs. PCRs with primers F1and R1 and with F3 and R3 amplified ∼800 base pairs of genomic sequences upstream and downstream of the stop codon of σ2 or of amino acid 236 of μ2, respectively. Primer R1 contains complementary sequences to the linker at the 5′ end of eGFP, and F3 primer contains complementary sequences to the 3′ end of the eGFP. The eGFP sequence containing the GGS linker was amplified using primers F2 and R2 from an eGFP expression plasmid used as template. Overlapping PCR performed using primers F1–R3 and the three DNA fragments (PCR products using primers F1 and R1, F2 and R2, and F3 and R3) as templates generated DNA fragments of eGFP open reading frame (ORF) flanked by either σ2 or μ2 genomic DNA sequences. These ∼2400–base pair PCR products were purified by electrophoresis in 1% agarose and cloned into pcDNA3.3 using a pcDNA3.3-TOPO TA cloning Kit (ThermoFisher Scientific).
The sequences of the σ2 primers were as follows:
| σ2.2 up | F1 AGTGGTGCAATCTTGGCTCATTGC |
|---|---|
| R1 GGAACCACCAGAACCACCAGAACCTCCC-TCCAGGGACTGTAGCATCAGC | |
| σ2.2 eGFP | F2 GTTCTGGTGGTTCTGGTGGTTCCCTGGTG-AGCAAGGGCGAGGAGCTG |
| R2 TTACTTGTACAGCTCGTCCATGCC | |
| σ2.2 down | F3 GGACGAGCTGTACAAGTAAGGGCAG-GCGAGCCCCA |
| R3 CCAGGTATGGTGGCACACATC |
The sequences of the μ2 primers were as follows:
| μ2 up | F1 GTCACAGATCACCAGCCAGGT |
|---|---|
| R1 GATCCACCGGATCCTCCTTGCTTCCCGCT-GCAAGCAGG | |
| μ2 eGFP | F2 GAAGCAAGGAGGATCCGGTGGATCTCTGGTGA-GCAAGGGCGAGG |
| R2 AGAACCACCAGAACCTCCCTTGT | |
| μ2 down | F3 CAAGGGAGGTTCTGGTGGTTCTTCAATTGCCAT-TGATGACTGCACC |
| R3 CATTACAAAGGGAAATGCCAAAGCAT |
SUM159 cells (1.5 × 105) were cotransfected with 800 ng each of the Cas9 expression plasmid, pcDNA3.3 vector containing the donor construct, and the free PCR DNA fragment expressing the small guide RNA. Double allele-edited monoclonal cell lines were obtained using the same procedure described to obtain the SUM-AP-2.1 cell line. In brief, transfected cells were expanded and single-cell sorted using flow cytometry for expression of eGFP. Single cells expressing eGFP were isolated, allowed to clonally expand, and screened by PCR for eGFP insertion in both alleles. The primers used with genomic DNA to identify SUM-AP-2.2 (expressing σ2-eGFP) were the same used to identify SUM-AP2-2.1. SUM-AP-2.3 (expressing μ2-eGFP) was identified using the PCR forward primer 5′ GAGCAAGCCCCTTTGTTTGG 3′ and reverse primer 5′ TGATGTCCTTGGTTGTGCGA 3′ targeting genomic regions in the vicinity of amino acid 236 of μ2; the size of the PCR products for wild-type and eGFP-inserted μ2 were 526 and 1279 base pairs, respectively.
Immunoprecipitation and Western blotting
SUM159 cells wild-type, gene-edited SUM-AP-2.1, or SUM159 cells stably expressing σ2-eGFP were trypsinized, washed in phosphate-buffered saline (PBS), and resuspended at 4°C in lysis buffer (50 mM HEPES, pH 7.4, 150 mM NaCl, 15 mM MgCl2, 1 mM ethylene glycol tetraacetic acid, 10% glycerol, and 1% Triton X-100) with a protease inhibitor cocktail (Roche). The lysate was centrifuged for 5 min at 800 × g at 4°C and then 10,000 × g for 10 min at 4°C. The cell lysate was then precleared by incubation with G-Sepharose beads (GE Healthcare) at 4°C on a rotator for 2 h, 30 min to exhaust the lysate with nonspecific binding to the beads. In parallel, G-Sepharose beads were incubated with the mouse monoclonal antibody 10A (Clairmont et al., 1997; Ehrlich et al., 2004; Aguet et al., 2013) raised against the β1/β2 subunit of AP-2 for 2 h at 4°C on a rotator. The antibody–beads complex was washed twice and subsequently incubated with precleared lysate for 2 h at 4°C on a rotator. The beads were then pelleted at 800 × g and washed twice in lysis buffer and twice in Tris-buffered saline (200 mM NaCl, 0.5% Tween-20, and 50 mM Tris, pH 7.4). SDS–PAGE and Western blotting were used to analyze the immunoprecipitated proteins. Electrophoretic transfer to polyvinylidene fluoride membranes was performed on an iBlot Gel Transfer device (Life Technologies). The membrane was treated for 1 h with 5% nonfat dry milk in PBS and 0.05% Tween-20 (PBST) at room temperature, followed by incubation overnight at 4°C with a rabbit monoclonal antibody raised against the σ2 subunit of AP-2 (ab128950; Abcam). After three 10-min washes with PBST, the membrane was incubated for 1 h with 1 mg/ml donkey anti-rabbit immunoglobulin G horseradish peroxidase–conjugated secondary antibody (GE Healthcare). After extensive washes with PBST, the membranes were imaged with a Las 3000 system (Fujifilm) using the LumiGLO Chemiluminescent Substrate (KPL).
Endocytosis assay using flow cytometry
SUM159-AP-2.1 cells plated in six-well plates and grown to 80% confluency were transfected with plasmids coding for CD8 chimera containing in its cytosolic tail the endocytic motif YAAL, EAAALL, or FANPXAY, using TransfeX transfection reagent (ATCC). The day after transfection, the cells were trypsinized, and one-sixth of the cells were replated in 12-well plates in triplicate for 24 h, after which the CD8 antibody uptake assay was performed. Cells were incubated with Alexa Fluor 647 anti-human CD8a antibody (clone RPA-T8; Biolegend) for 15 min at 4 or 37°C. After incubation, the plates were cooled on ice, rinsed with ice-chilled PBS, and briefly incubated or not twice with 150 mM NaCl, 1 mM MgCl2, 0.125 mM CaCl2, and 0.1 M glycine, pH 2.5, to remove the surface-bound CD8-A647 antibody. The cells were then resuspended, rinsed with 200 μl SUM medium, and resuspended in 200 μl of PBS containing 1% bovine serum albumin and 0.5 mM EDTA at 4°C. The amount of CD8 antibody associated with each cell, reflecting the extent of endocytosis, was determined by flow cytometry as the mean fluorescence intensity of CD8-A647 after the acid wash, using the 633-nm laser line of the FASCSCanto II (BD Biosciences).
TIRF microscopy visualization and corresponding analyses
Glass coverslips (#1.5; Warner Instruments, Hamden, CT) were cleaned by sonication for 15 min in 100% ethanol, dried, and then coated with a copolymer of poly-l-lysine and biotinylated poly(ethylene glycol) (PEG; Susos AG) as described (Böcking et al., 2011; Cocucci et al., 2012, 2014). The PEG-modified coverslips were coated with 0.2 mg/ml avidin dissolved in PBS, and after extensive wash with PBS, they were coated with 0.5 mg/ml biotinylated fibronectin dissolved in PBS. After rinsing, the coverslips were used to plate cells for TIRF microscopy.
Glass coverslips with plated cells were washed with sterile PBS and placed in an Attofluor Cell Chamber (Invitrogen, Carlsbad, CA) with 1 ml of prewarmed MEMα without phenol red (GIBCO, Langley, OK) supplemented with 1% FBS. The chamber was then placed into a heated sample holder (20/20 Technology, Wilmington, NC) placed inside the environmentally controlled chamber of the TIRF microscope.
Recombinant eGFP made in Escherichia coli was used for single-molecule fluorescence intensity calibration as described (Cocucci et al., 2012; Kural et al., 2012). TIRF imaging was carried out of coverslips bound to eGFP from a solution containing ∼2 nM eGFP in PBS adsorbed immediately after a 5-min glow discharge at 50 mA (Electron Microscopy Science, Hatfield, PA).
TIRF microscopy was performed using a Marianas–based system (Intelligent Imaging Innovations, Denver, CO) controlled with SlideBook V5.0 (Intelligent Imaging) operating under Windows 7 (Microsoft) on a computer with 12 GB of RAM (Dell, Round Rock, TX) as described (Cocucci et al., 2012, 2014), except that the spherical aberration correction system was replaced by a 2× magnification lens placed in front of the charge-coupled device (CCD) camera, such that each pixel corresponded to 80 nm in object space. The incidence angle of the excitation light was adjusted to generate an evanescent field with a penetration depth of ∼100–200 nm. The illumination power at the back aperture of the objective was 3.3 mW. Time series were acquired with an exposure of 60 ms/frame imaged every 150 ms.
The dynamics of cytosolic AP-2 incorporation during the first 5 s of pit formation was determined from TIRF data with single-molecule sensitivity acquired using gene-edited SUM-AP-2.1 cells as described (Cocucci et al., 2012, 2014). The centroid of diffraction-limited spots was obtained using the u-track software (Jaqaman et al., 2008; Aguet et al., 2013) with psfSigma, 1; integWindow, 1; alphaLocMax, 0.12; and numSigmaIter, 3. Tracking was constrained to objects that remained for at least 15 consecutive frames (∼1.7 s) and with gaps of <5 frames. The selected traces persisted for 15 s or more. Step detection during the initial growth phase of the tracings was done as previously described (Cocucci et al., 2012).
Independent confirmation for the full extent of substitution determined by Western blot analysis from SUM-AP-2.1 cell extracts was obtained by comparing models with variable substitution levels and different combinations of AP-2 recruitment units (monomer, dimer, tetramer, dimers and tetramers, etc.) and using the BIC to search for the model that would best fit the experimental data (Burnham and Anderson, 2002; Cocucci et al., 2012).
LLSM visualization of cells ex vivo and corresponding analyses
Cell cycle synchronization and ex vivo imaging during cell division.
After keeping the cells at 100% confluency for 1 d (a condition that arrests the cells at the end of G1; Coupin et al., 1999; Kozik et al., 2010), they were trypsinized and seeded onto 5-mm-diameter coverslips (Warner Instruments) that were cleaned by sonication in 95% ethanol at ∼30–50% confluency; this procedure helped to synchronize cell division and increase the proportion of cells entering S phase. The cells in prometaphase and metaphase were identified by their spherical appearance 11–16 h after plating. The cells were then imaged in Leibovitz’s L-15 medium without phenol red (21083-027; Life Technologies) supplemented with 5% FBS and 20 mM HEPES, pH 7.4.
LLSM live-cell 3D imaging.
The imaging of gene-edited SUM-AP-2.1 cells was carried out in two labs using the LLSM.1 from the Betzig laboratory at the Howard Hughes Medical Institute Janelia Research Campus (Ashburn, VA) and the LLSM.2 from the Kirchhausen laboratory (Harvard Medical School, Boston, MA). In both microscopes, we generated a light sheet using a square lattice configuration in dithered mode (Chen et al., 2014). The LLSM.1 data were acquired using an Andor iXon 897 electron-multiplying (EM) CCD camera in which the sample was collected by exciting each plane with a 488- nm laser at ∼62 μW (at the back aperture of the excitation objective) for 20 ms and with excitation inner and outer numerical apertures (NAs) of 0.325 and 0.4, respectively. The LLSM.2 data from gene-edited SUM-AP-2.1, SUM-AP-2.2, and SUM AP-2.3 were acquired with either a Hamamatsu ORCA-Flash 4.0 scientific complementary metal-oxide semiconductor (sCMOS) camera or an Andor iXon 897 EMCCD camera, in which each plane of the imaged volume was exposed for 40 ms and excited using a 488-nm laser (operating at _∼_6 mW, with ∼20 μW at the back aperture of the excitation objective) with an excitation NA of 0.35/0.44 and a corresponding light-sheet length of 30 μm. SUM-AP-2.1 cells undergoing division were imagined by scanning the objective and the dithered light sheet at 500-nm step sizes in the _z_-axis (see schematic representation in Figure 3A), thereby capturing a volume of _∼_50 × 50 × 25 μm (512 × 512 × 51 pixels) on the LLSM.1 or ∼ 80 × 80 × 35 μm on the LLSM.2 (768 × 768 × 70 pixels) every 2.4–2.8 s (including a 1.5-s pause between time points for data acquired on the LLSM.1). Measurements of coated-pit dynamics and determination of surface area and volume changes of cells undergoing mitosis were obtained by continuous imaging periods of 2.5 min, followed by ∼2-min pause. Interphase SUM-AP-2.1 cells were imagined by scanning the sample stage with step sizes of 450 nm (LLSM.1) or 500 nm (LLSM.2) and excitation NA of 0.44/0.55 (LLSM.1) or 0.35/0.44 (LLSM.2). The _z_-axis step sizes were ∼235 or ∼261 nm, corresponding to pre-deskewed volume data sets of _∼_13 × 50 × 36 μm or 128 × 512 × 81 pixels (LLSM.1) and ∼80 × 80 × 35 μm or 768 × 768 × 70 pixels (LLSM.2), respectively. The time series lasted 5 min, and each stack was obtained during a period of ∼2.8–3.0 s (which included a 1.5-s pause between time points for data acquired using LLSM.1).
The BSC1 CAAX-eGFP-H2B-mCherry cells were prepared and plated as described for the SUM-AP-2.1 cells. These cells were imaged using LLSM.1 with an excitation NA of 0.325/0.4; eGFP-CAAX was excited using a 488-nm laser operating at ∼68 μW, and H2B-mCherry was excited using a 560-nm laser operating at ∼20 μW. Each plane was imaged for 30 ms and spaced 250 nm apart along the _z_-axis (see schematic representation in Figure 3A) by jointly scanning the detection objective and the dithered light sheet; a total volume of ∼ 50 × 50 × 38 μm was continuously imaged every 120 s. Time series used to generate figures and, when indicated, movies were deconvolved in MATLAB using the Lucy–Richardson algorithm (deconvlucy function in MATLAB) by providing measured background and an experimentally measured PSF for 15 iterations on a 3-GHz 8-core Intel Xeon E5 Apple Mac Pro with 128 GB of memory. Most 3D renderings were generated using FEI’s Amira versions 5.6 and 6.0. Both LLSMs were operated using custom LabVIEW (National Instruments) software on a 3.47-GHz Intel Xeon X5690 workstation with 96 GB of memory running a Windows 7 operating system.
Postprocessing of raw data volumes.
Data volumes were acquired as multipage TIFF files, with each slice of a volume corresponding to a cross-section of the sample. The images in the raw data appeared as a shear-transformed representation of the sample because the samples visualized with scan mode (sample moved along the s-axis) were scanned at a fixed angle to the glass coverslip of 32.8° (LLSM.1) or 31.5° (LLSM.2). To enable data processing in real-world coordinates, these volumes were deskewed using an inverse shear transform (imwarp function in MATLAB). Visualization of the volumetric images was further facilitated by presenting the coverslip oriented horizontally, after applying a scaling factor to correct for anisotropy between x, y, and z sampling, followed by rotation by the scanning angle.
Automated detection in three dimensions of clathrin-coated structures.
Fluorescence-tagged clathrin-coated structures generate a diffraction-limited signal and are therefore accurately detected through numerical fitting with a model of the microscope PSF. The shape of this function for the lattice light-sheet microscope is well approximated by a 3D Gaussian function. Owing to the separability (by multiplication) of a multidimensional Gaussian function into its one-dimensional components, this approximation leads to a computationally efficient approach for the detection of diffraction-limited signals. To this end, we generalized an approach developed for TIRF microscopy, which relied on a Gaussian model for the detection of diffraction-limited spot signals in 2D data (Aguet et al., 2013). A key component of the method is an efficient, filter-based implementation of a t test to determine the statistical significance of the fluorescence at every voxel in a data volume. Briefly, the approach consists of the following three steps: 1) identification of voxels containing a statistically significant fluorescence signal; 2) numerical fitting of a 3D Gaussian model at every location with significant signal to determine fluorescence intensity and subvoxel localization; 3) statistical testing of the fitted intensity against background signal. The proposed detection framework is based on the assumption that the fluorescence signals measured from coated pits can be described by a Gaussian PSF function and by an additive white Gaussian noise term (Aguet et al., 2013). We verified the validity of this approximation for LLSM data by testing areas of homogeneous background and residual signals for normality using the Anderson–Darling test. In the proposed framework, the 3D image of a coated pit was thus modeled as
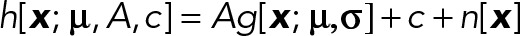
where 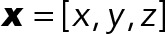 are discrete voxel coordinates, A is the fluorescence amplitude, c is a constant representing the local background intensity for the coated pit, and
are discrete voxel coordinates, A is the fluorescence amplitude, c is a constant representing the local background intensity for the coated pit, and 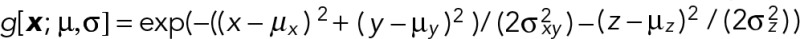 defines the Gaussian approximation of the microscope PSF. The SDs σ_xy_ and σ_z_, denoted vectorially as σ, are fixed parameters and will henceforth be omitted from the notation for simplicity; their estimation is described at the end of this section. Noise was assumed to follow a Gaussian distribution with SD σ_r_ over the support of the coated pit, that is,
defines the Gaussian approximation of the microscope PSF. The SDs σ_xy_ and σ_z_, denoted vectorially as σ, are fixed parameters and will henceforth be omitted from the notation for simplicity; their estimation is described at the end of this section. Noise was assumed to follow a Gaussian distribution with SD σ_r_ over the support of the coated pit, that is, 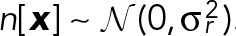 . The problem of detecting a diffraction-limited signal can then be formulated as a least-squares minimization problem: at a candidate location, the parameters, µ, A and c of the model are estimated around a candidate location k = [_k_1, _k_2] in an image volume f [_x_] by subvoxel localization through the minimization of
. The problem of detecting a diffraction-limited signal can then be formulated as a least-squares minimization problem: at a candidate location, the parameters, µ, A and c of the model are estimated around a candidate location k = [_k_1, _k_2] in an image volume f [_x_] by subvoxel localization through the minimization of
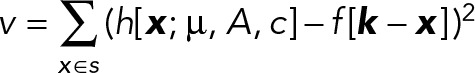 (1)
(1)
The spatial support was defined as 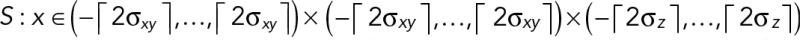 centered on k. Coated-pit fluorescence was considered significant and retained for further analysis if the estimated amplitude  was above a defined threshold level of the local background noise distribution (see later discussion).
centered on k. Coated-pit fluorescence was considered significant and retained for further analysis if the estimated amplitude  was above a defined threshold level of the local background noise distribution (see later discussion).
Using the foregoing model, we obtain a pixel-level mask of significant signal positions by minimizing
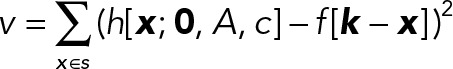
at each voxel k in frame f, i.e., by minimizing
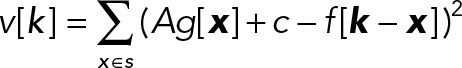
where _g_[_x_] denotes _g_[x; 0]. Specifically, estimates of the amplitude A and local background c for the Gaussian centered at each voxel k are obtained by solving the system
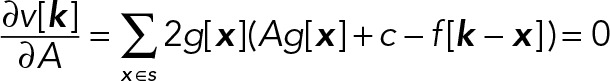
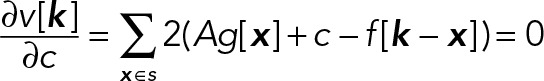
yielding
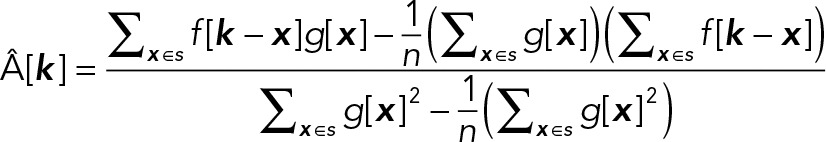
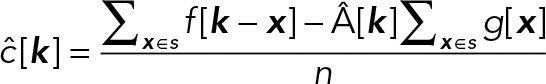
where n is the number of voxels in S. By defining 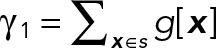 and
and 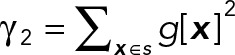 (this is numerically more accurate than using the corresponding analytical values), we can rewrite these equations as
(this is numerically more accurate than using the corresponding analytical values), we can rewrite these equations as
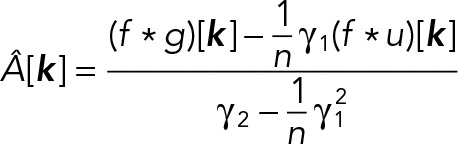
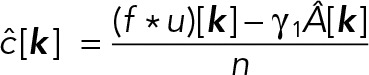
where the asterisk denotes convolution and _u_[_x_] is a summation filter defined over S, that is, _u_[_x_] = 1 if x ∈ S; 0 otherwise.
To identify voxels with a significant value of  by means of a statistical test, estimates of the uncertainties on  and the background noise, given by the residuals of the fit, are needed. At each voxel k, the residual sum of squares (RSS) of the fit is given by
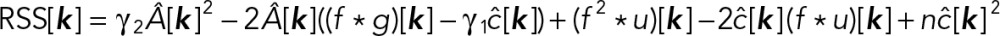
and the variance of the residuals is calculated as
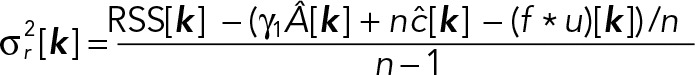
The uncertainty (SD) on _Â_[_k_] is obtained by error propagation:
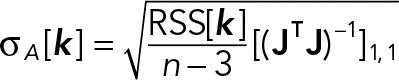
where J = [g1] is the Jacobian matrix (identical for all voxel positions), g is the column-vector representation of _g_[_x_], and 1 is the unit vector. The probability densities of the fluorescence amplitude and noise in support S at each voxel are 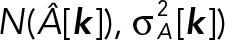
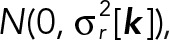 respectively.
respectively.
An estimated amplitude was considered significant if its value was above a threshold value κσr of the noise distribution, where 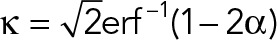 and α is the significance level (i.e., α = 0.05). Significance was determined using a one-sided, two-sample t test with _H_0: Â ≤ κσr, yielding the statistic
and α is the significance level (i.e., α = 0.05). Significance was determined using a one-sided, two-sample t test with _H_0: Â ≤ κσr, yielding the statistic
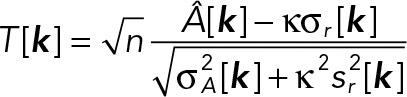 (2)
(2)
where the uncertainty on σr is calculated using an estimator for the SE of the variance:
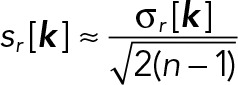
A mask of significant voxels was then obtained as _m_[_k_]: = _p_[_k_] < α, where p is the p value of the test.
Candidate coated-pit signals were identified as statistically significant voxels _m_[_k_] in that coincided with local maxima of the 3D Laplacian-of-Gaussian filtered image volume f [_x_] (Aguet et al., 2013). At each candidate location, a 3D Gaussian fit was performed by minimization of Eq. 1, yielding estimates of A, c, and μ at subvoxel resolution. The significance of the resulting amplitude estimate  was then tested using Eq. 2.
In areas of high coated-pit density, local maxima occurring within the same mask region were either localized individually or through a mixture-model extension of the fitting approach, replacing the single Gaussian in Eq. 1 with a sum of Gaussians. In the latter case, automated selection of the optimal number of mixture components was performed based on iterative F tests incrementally identifying the statistical justification for additional components. In all instances, each estimated amplitude was individually tested for significance based on the criterion of Eq. 2. The algorithm was implemented as a C/MEX function for MATLAB (MathWorks, Natick, MA) using nonlinear optimization routines from the GNU Scientific Library (https://www.gnu.org/software/gsl/). These routines provide a robust and efficient implementation of the Levenberg–Marquardt algorithm.
The SDs σxy and σz of the 3D Gaussian PSF were precalculated by fitting the model to an average of bright coated-pit signals or to PSF measurements obtained with fluorescent beads with the SDs as free parameters.
Automated tracking of clathrin-coated structure dynamics.
Coated pit trajectories were calculated from the detections obtained in individual frames with the u-track software package (Jaqaman et al., 2008), using the parameters described in Aguet et al. (2013). The u-track software implements tracking in a generic _n_-dimensional framework, and thus few adaptations were required. Positions in voxel coordinates were rescaled to correct for _z_-anisotropy. Tracking was performed using positional information only (ignoring amplitude values), and merging and splitting of tracks was enabled. Coated structures forming in close vicinity (i.e., within the search radius used for linking individual detections) were thus identified as compound tracks and excluded from further analysis. Tracks were postprocessed to identify valid trajectories as described in Aguet et al. (2013).
Calculation of lifetime distributions and intensity cohorts.
Lifetime distributions, intensity cohorts, and initiation density statistics were calculated as described in Aguet et al. (2013). Event densities were calculated using all trajectories with lifetimes of >10 or >25 s (equivalent to at least four to eight _z_-stacks, respectively) without the need to include filtering of trajectories with gaps (missing frames) because of the relatively high signal-to-noise ratios of the LLSM data.
Surface area and volume measurements.
The signal-to-noise ratio of cytosolic signal relative to background in SUM-AP-2.1 cell data was sufficiently high to apply threshold-based segmentation to generate a mask of the cell outline. Specifically, cell masks were obtained by 1) smoothing the deskewed data volumes with a Gaussian filter (SD = 2) and interpolating to isotropic voxels, 2) applying the Otsu thresholding method, and 3) closing potential holes resulting from lower fluorescence at chromatid locations (using the imfill function in MATLAB). Surface area and volume traces extracted from BSC1 cells and zebrafish eye and spinal tissue were smoothed using the smooth function with the default parameters in MATLAB.
Implementation.
All image and data analyses were carried out in MATLAB, using custom-written software available from https://github.com/francois-a/llsmtools.
Zebrafish embryos
Animal studies.
Zebrafish work was carried out with the approval of Institutional Animal Care and Use Committee at Harvard University under Protocol 04487.
Crossing of zebrafish embryos.
To image dividing cells in the developing eye of zebrafish, we used 1) the fluorescent transgenic zebrafish strain Tg(actb2:mem-citrine-citrine)hm30 and 2) Tg(actb2:mem-citrine)/(actb2:Hsa.H2b-tdTomato)hm32,hm33, where hm32 and hm33 are two separate alleles of divergent constructs. These three alleles were combined for the brightest membrane signal. The transgenic was generated using the Tol2 method (Gao et al., 2014), where mem corresponds to two copies of the plasma membrane–localized palmitoylation/myristoylation motif of lyn kinase of the sequence ATGGGCTGCATCAAGAGCAAGCGCAAGGACAACCTGAACGACGACGAGGCCGCCATGGGCTGCATCAAGAGCAAGCGCAAGGACAACCTGAACGACGACGAG fused to citrine and expressed in all cells (the marker used for membrane imaging; Mosaliganti et al., 2012). Mosaic zebrafish were generated using wild-type animals injected at the 4- to 16-cell stage with 2.3 nl of 10–20 ng/μl mRNA encoding _mem_-citrine (Megason, 2009). For each zebrafish pair, male and female fish were set up the previous night in crossing tanks with a separator the and subsequently crossed in the morning using natural spawning methods. The eggs were collected and screened for health before being transferred to a 28°C incubator and kept at this temperature, except during injection/dechorionation and imaging, which were performed at room temperature. Natural twitching of embryos when visualized beyond 20 h postfertilization was prevented by injection into 1-cell-stage embryos of 2.3 nl of 20 ng/μl mRNA encoding α-bungarotoxin used as anesthetic (Swinburne et al., 2015). Injections were performed using a glass needle (15- to 25-μm diameter) with the Nanoinject system and a Leica stereoscope (Leica MZ12.5). The time postfertilization was recorded according to the single-cell stage of each clutch aligned according to the normal table (Kimmel et al., 1995). All zebrafish were housed in fully equipped, regularly maintained, and fully inspected aquarium facilities at Harvard Medical School.
Mounting of zebrafish embryos.
To ensure proper development and adequate expression of _mem_-citrine and before mounting in the stage of the LLSM, the zebrafish embryos were screened using a Leica stereomicroscope for their health and fluorescence brightness. The embryos were then carefully placed in the center of a 5-mm-diameter glass coverslip (CS-5R; Warner Instruments) directly above a drop of rapidly setting 1% (wt/wt; in 1× Danieau buffer) low-melt agarose (UltraPure Low Melting Point Agarose; LMA). During the fluid agarose phase, suspended embryos were gently nudged using a hair-loop to occupy a dorsolateral position; this orientation prevented possible occlusion from the yolk during the imaging at 17–24 h postfertilization of the eyes and the spinal cord. Excessive deterioration of the quality of the light sheet generated by LLSM and reduced light scattering by the agarose was avoided by using Kimmel tissue paper to remove by wicking the extra fluid above the zebrafish before solidification.
LLSM in vivo imaging of zebrafish embryos.
The zebrafish embryos were imaged using the LLSM.2 from the Kirchhausen laboratory in 1× Danieau buffer at 22 ± 2ºC starting at 17–22 h postfertilization. A light sheet was generated using a square lattice configuration in dithered mode. Each plane of tissue was illuminated for 40 ms using a 488-nm laser operating at _∼_6 mW, with ∼20 μW measured at the back aperture of the excitation objective. The inner and outer NAs of excitation were 0.35 and 0.44, respectively, with a beam length on the light sheet of >100 μm; the nondiffracting region used for imaging had an approximate length of 30 μm. The optical planes were acquired with a Hamamatsu ORCA-Flash 4.0 sCMOS camera. Cells in the developing eye were imagined by scanning the sample stage with a 400-nm step size along the s-axis, equivalent to ∼209-nm steps along the _z_-axis (see schematic representation in Figure 7A), capturing a volume of _∼_80 × 80 × 100 μm every 16.0 s (including a 6-s pause between _z_-stacks). At each time point, we recorded an image stack volume deskewed at 31.5° and stored as 32-bit images to avoid rounding errors from the interpolated image slices; the image stacks were then cropped to 768 × 768 × 251 pixels and used for surface area and volume determinations. The LLSM.2 was under control of custom LabVIEW (National Instruments) software operating on a 3.47-GHz Intel Xeon X5690 workstation with 96 GB of memory under Windows 7 operating system. As indicated, the zebrafish figures and movies were deconvolved for 15 iterations using the Lucy–Richardson algorithm in MATLAB with an experimentally measured PSF. This postacquisition processing was done immediately after acquisition using a 3-GHz eight-core Intel Xeon E5 Apple Mac Pro with 128 GB of memory.
Detection and analysis of surface area and volume in isolated BSC1 cells and cells in zebrafish embryos.
The single BSC1 cells and the multicellular assemblies in the imaged tissues were segmented using ACME (Mosaliganti et al., 2012). Briefly, the deskewed images were 1) preprocessed using a median filter to remove high-frequency noise, 2) down-sampled to make x-, y-, and _z_-voxels isotropic, which is necessary for optimal watershed operation, 3) filtered using a combination of a Hessian matrix of the intensity function and normalized Gaussian derivatives for planarity detection to locate membrane planes, 4) tensor voted to fill any structural gaps in the membrane voxels, and 5) segmented using the watershed algorithm, in which the salient images generated from tensor voting served as a topographic map for robustly delineating cell boundaries. Errors in segmentation (primarily hypersegmentation) were manually corrected, and the cells were linked over time to compute and track the changes in surface area and volume. The surface area and volumes were calculated in MATLAB using the generated (and manually corrected, when necessary) watershed masks. The original ACME segmentation source code was modified and compiled to take advantage of the dynamic range of the 16-bit images acquired from the BSC1 cells expressing the eGFP-CAAX fluorescence plasma membrane marker, and the subsequent processing of segmentation corrections and surface area/volume calculations were performed as described for the zebrafish images.
Supplementary Material
Supplemental Materials
Acknowledgments
We thank Ian Swinburne from Sean Megason’s laboratory for helpful advice and discussions associated with the zebrafish work and Margaret Robinson for the CD chimera constructs. S.U. is a Fellow at the Image and Data Analysis Core at Harvard Medical School and thanks Hunter Elliott and Tiao Xie for helpful discussions. T.K. gratefully acknowledges support from the Janelia Visitor Program. The construction of the lattice light-sheet microscope LLSM.2 in the Kirchhausen laboratory was generously supported by grants from Biogen and IONIS Pharmaceuticals (to T.K.). This work was supported by National Institutes of Health Grants R01 GM075252 (T.K.) and K25 HD071969 (K.M.).
Abbreviations used:
ACME
Automated Cell Morphology Extractor
BIC
Bayesian information criterion
GFP
green fluorescent protein
LLSM
lattice light-sheet microscope
PSF
point spread function
TIRF
total internal reflection fluorescence.
Footnotes
REFERENCES
- Aguet F, Antonescu CN, Mettlen M, Schmid SL, Danuser G. Advances in analysis of low signal-to-noise images link dynamin and AP2 to the functions of an endocytic checkpoint. Dev Cell. 2013;26:279–291. doi: 10.1016/j.devcel.2013.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahle S, Mann A, Eichelsbacher U, Ungewickell E. Structural relationships between clathrin assembly proteins from the Golgi and the plasma membrane. EMBO J. 1988;7:919–929. doi: 10.1002/j.1460-2075.1988.tb02897.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boucrot E, Kirchhausen T. Endosomal recycling controls plasma membrane area during mitosis. Proc Natl Acad Sci USA. 2007;104:7939–7944. doi: 10.1073/pnas.0702511104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boucrot E, Kirchhausen T. Mammalian cells change volume during mitosis. PLoS One. 2008;3:e1477. doi: 10.1371/journal.pone.0001477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boucrot E, Saffarian S, Massol R, Kirchhausen T, Ehrlich M. Role of lipids and actin in the formation of clathrin-coated pits. Exp Cell Res. 2006;312:4036–4048. doi: 10.1016/j.yexcr.2006.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boulant S, Kural C, Zeeh J-C, Ubelmann F, Kirchhausen T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nat Cell Biol. 2011;13:1124–1131. doi: 10.1038/ncb2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böcking T, Aguet F, Harrison SC, Kirchhausen T. Single-molecule analysis of a molecular disassemblase reveals the mechanism of Hsc70-driven clathrin uncoating. Nat Struct Mol Biol. 2011;18:295–301. doi: 10.1038/nsmb.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Model Selection and Multimodel Inference. New York: Springer; 2002. [Google Scholar]
- Chen B-C, Legant WR, Wang K, Shao L, Milkie DE, Davidson MW, Janetopoulos C, Wu XS, Hammer JA, Liu Z, et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science. 2014;346:1257998. doi: 10.1126/science.1257998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou Y-Y, Cuevas C, Carocci M, Stubbs SH, Ma M, Cureton DK, Chao L, Evesson F, He K, Yang PL, et al. Identification and characterization of a novel broad spectrum virus entry inhibitor. J Virol. 2016;90:4494–4510. doi: 10.1128/JVI.00103-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clairmont KB, Boll W, Ericsson M, Kirchhausen T. A role for the hinge/ear domain of the beta chains in the incorporation of AP complexes into clathrin-coated pits and coated vesicles. Cell Mol Life Sci. 1997;53:611–619. doi: 10.1007/s000180050080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocucci E, Aguet F, Boulant S, Kirchhausen T. The first five seconds in the life of a clathrin-coated pit. Cell. 2012;150:495–507. doi: 10.1016/j.cell.2012.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocucci E, Gaudin R, Kirchhausen T. Dynamin recruitment and membrane scission at the neck of a clathrin-coated pit. Mol Biol Cell. 2014;25:3595–3609. doi: 10.1091/mbc.E14-07-1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupin GT, Muller CD, Rémy-Kristensen A, Kuhry JG. Cell surface membrane homeostasis and intracellular membrane traffic balance in mouse L929 cells. J Cell Sci. 1999;112:2431–2440. doi: 10.1242/jcs.112.14.2431. [DOI] [PubMed] [Google Scholar]
- Doyon JB, Zeitler B, Cheng J, Cheng AT, Cherone JM, Santiago Y, Lee AH, Vo TD, Doyon Y, Miller JC, et al. Rapid and efficient clathrin-mediated endocytosis revealed in genome-edited mammalian cells. Nat Cell Biol. 2011;13:331–337. doi: 10.1038/ncb2175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrlich M, Boll W, van Oijen A, Hariharan R, Chandran K, Nibert ML, Kirchhausen T. Endocytosis by random initiation and stabilization of clathrin-coated pits. Cell. 2004;118:591–605. doi: 10.1016/j.cell.2004.08.017. [DOI] [PubMed] [Google Scholar]
- Fielding AB, Willox AK, Okeke E, Royle SJ. Clathrin-mediated endocytosis is inhibited during mitosis. Proc Natl Acad Sci USA. 2012;109:6572–6577. doi: 10.1073/pnas.1117401109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer-Friedrich E, Hyman AA, Jülicher F, Muller DJ, Helenius J. Quantification of surface tension and internal pressure generated by single mitotic cells. Sci Rep. 2014;4:6213. doi: 10.1038/srep06213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao L, Shao L, Chen B-C, Betzig E. 3D live fluorescence imaging of cellular dynamics using Bessel beam plane illumination microscopy. Nat Protoc. 2014;9:1083–1101. doi: 10.1038/nprot.2014.087. [DOI] [PubMed] [Google Scholar]
- Grassart A, Cheng AT, Hong SH, Zhang F, Zenzer N, Feng Y, Briner DM, Davis GD, Malkov D, Drubin DG. Actin and dynamin2 dynamics and interplay during clathrin-mediated endocytosis. J Cell Biol. 2014;205:721–735. doi: 10.1083/jcb.201403041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grove J, Metcalf DJ, Knight AE, Wavre-Shapton ST, Sun T, Protonotarios ED, Griffin LD, Lippincott-Schwartz J, Marsh M. Flat clathrin lattices: stable features of the plasma membrane. Mol Biol Cell. 2014;25:3581–3594. doi: 10.1091/mbc.E14-06-1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grover WH, Bryan AK, Diez-Silva M, Suresh S, Higgins JM, Manalis SR. Measuring single-cell density. Proc Natl Acad Sci USA. 2011;108:10992–10996. doi: 10.1073/pnas.1104651108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habela CW, Sontheimer H. Cytoplasmic volume condensation is an integral part of mitosis. Cell Cycle. 2007;6:1613–1620. doi: 10.4161/cc.6.13.4357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong SH, Cortesio CL, Drubin DG. Machine-learning-based analysis in genome-edited cells reveals the efficiency of clathrin-mediated endocytosis. Cell Rep. 2015;12:2121–2130. doi: 10.1016/j.celrep.2015.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid SL, Danuser G. Robust single-particle tracking in live-cell time-lapse sequences. Nat Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaur S, Fielding AB, Gassner G, Carter NJ, Royle SJ. An unmet actin requirement explains the mitotic inhibition of clathrin-mediated endocytosis. Elife. 2014;3:e00829. doi: 10.7554/eLife.00829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimmel CB, Ballard WW, Kimmel SR, Ullmann B, Schilling TF. Stages of embryonic development of the zebrafish. Dev Dyn. 1995;203:253–310. doi: 10.1002/aja.1002030302. [DOI] [PubMed] [Google Scholar]
- Kirchhausen T. Imaging endocytic clathrin structures in living cells. Trends Cell Biol. 2009;19:596–605. doi: 10.1016/j.tcb.2009.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozik P, Francis RW, Seaman MNJ, Robinson MS. A screen for endocytic motifs. Traffic. 2010;11:843–855. doi: 10.1111/j.1600-0854.2010.01056.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kural C, Akatay AA, Gaudin R, Chen B-C, Legant WR, Betzig E, Kirchhausen T. Asymmetric formation of coated pits on dorsal and ventral surfaces at the leading edges of motile cells and on protrusions of immobile cells. Mol Biol Cell. 2015;26:2044–2053. doi: 10.1091/mbc.E15-01-0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kural C, Tacheva-Grigorova SK, Boulant S, Cocucci E, Baust T, Duarte D, Kirchhausen T. Dynamics of intracellular clathrin/AP1- and clathrin/AP3-containing carriers. Cell Rep. 2012;2:1111–1119. doi: 10.1016/j.celrep.2012.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu AP, Aguet F, Danuser G, Schmid SL. Local clustering of transferrin receptors promotes clathrin-coated pit initiation. J Cell Biol. 2010;191:1381–1393. doi: 10.1083/jcb.201008117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megason SG. In toto imaging of embryogenesis with confocal time-lapse microscopy. Methods Mol Biol. 2009;546:317–332. doi: 10.1007/978-1-60327-977-2_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrifield CJ, Kaksonen M. Endocytic accessory factors and regulation of clathrin-mediated endocytosis. Cold Spring Harb Perspect Biol. 2014;6:a016733. doi: 10.1101/cshperspect.a016733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrifield CJ, Feldman ME, Wan L, Almers W. Imaging actin and dynamin recruitment during invagination of single clathrin-coated pits. Nat Cell Biol. 2002;4:691–698. doi: 10.1038/ncb837. [DOI] [PubMed] [Google Scholar]
- Merrifield CJ, Perrais D, Zenisek D. Coupling between clathrin-coated-pit invagination, cortactin recruitment, and membrane scission observed in live cells. Cell. 2005;121:593–606. doi: 10.1016/j.cell.2005.03.015. [DOI] [PubMed] [Google Scholar]
- Mosaliganti KR, Noche RR, Xiong F, Swinburne IA, Megason SG. ACME: automated cell morphology extractor for comprehensive reconstruction of cell membranes. PLoS Comput Biol. 2012;8:e1002780. doi: 10.1371/journal.pcbi.1002780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozlu N, Qureshi MH, Toyoda Y, Renard BY, Mollaoglu G, Ozkan NE, Bulbul S, Poser I, Timm W, Hyman AA, et al. Quantitative comparison of a human cancer cell surface proteome between interphase and mitosis. EMBO J. 2014;34:251–265. doi: 10.15252/embj.201385162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ran FA, Hsu PD, Wright J, Agarwala V, Scott DA, Zhang F. Genome engineering using the CRISPR-Cas9 system. Nat Protoc. 2013;8:2281–2308. doi: 10.1038/nprot.2013.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MS. 100-kD coated vesicle proteins: molecular heterogeneity and intracellular distribution studied with monoclonal antibodies. J Cell Biol. 1987;104:887–895. doi: 10.1083/jcb.104.4.887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saffarian S, Cocucci E, Kirchhausen T. Distinct dynamics of endocytic clathrin-coated pits and coated plaques. PLoS Biol. 2009;7:e1000191. doi: 10.1371/journal.pbio.1000191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saffarian S, Kirchhausen T. Differential evanescence nanometry: live-cell fluorescence measurements with 10-nm axial resolution on the plasma membrane. Biophys J. 2008;94:2333–2342. doi: 10.1529/biophysj.107.117234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjana NE, Cong L, Zhou Y, Cunniff MM, Feng G, Zhang F. A transcription activator-like effector toolbox for genome engineering. Nat Protoc. 2012;7:171–192. doi: 10.1038/nprot.2011.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Son S, Kang JH, Oh S, Kirschner MW, Mitchison TJ, Manalis S. Resonant microchannel volume and mass measurements show that suspended cells swell during mitosis. J Cell Biol. 2015;211:757–763. doi: 10.1083/jcb.201505058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart MP, Helenius J, Toyoda Y, Ramanathan SP, Muller DJ, Hyman AA. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469:226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- Swinburne IA, Mosaliganti KR, Green AA, Megason SG. Improved long-term imaging of embryos with genetically encoded α-bungarotoxin. PLoS One. 2015;10:e0134005. doi: 10.1371/journal.pone.0134005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tacheva-Grigorova SK, Santos AJM, Boucrot E, Kirchhausen T. Clathrin-mediated endocytosis persists during unperturbed mitosis. Cell Rep. 2013;4:659–668. doi: 10.1016/j.celrep.2013.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor MJ, Perrais D, Merrifield CJ. A high precision survey of the molecular dynamics of mammalian clathrin-mediated endocytosis. PLoS Biol. 2011;9:e1000604. doi: 10.1371/journal.pbio.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zlotek-Zlotkiewicz E, Monnier S, Cappello G, Le Berre M, Piel M. Optical volume and mass measurements show that mammalian cells swell during mitosis. J Cell Biol. 2015;211:765–774. doi: 10.1083/jcb.201505056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoncu R, Perera RM, Sebastian R, Nakatsu F, Chen H, Balla T, Ayala G, Toomre D, De Camilli PV. Loss of endocytic clathrin-coated pits upon acute depletion of phosphatidylinositol 4,5-bisphosphate. Proc Natl Acad Sci USA. 2007;104:3793–3798. doi: 10.1073/pnas.0611733104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Materials