Uncovering transcriptional regulation of metabolism by using metabolic network topology (original) (raw)
Abstract
Cellular response to genetic and environmental perturbations is often reflected and/or mediated through changes in the metabolism, because the latter plays a key role in providing Gibbs free energy and precursors for biosynthesis. Such metabolic changes are often exerted through transcriptional changes induced by complex regulatory mechanisms coordinating the activity of different metabolic pathways. It is difficult to map such global transcriptional responses by using traditional methods, because many genes in the metabolic network have relatively small changes at their transcription level. We therefore developed an algorithm that is based on hypothesis-driven data analysis to uncover the transcriptional regulatory architecture of metabolic networks. By using information on the metabolic network topology from genome-scale metabolic reconstruction, we show that it is possible to reveal patterns in the metabolic network that follow a common transcriptional response. Thus, the algorithm enables identification of so-called reporter metabolites (metabolites around which the most significant transcriptional changes occur) and a set of connected genes with significant and coordinated response to genetic or environmental perturbations. We find that cells respond to perturbations by changing the expression pattern of several genes involved in the specific part(s) of the metabolism in which a perturbation is introduced. These changes then are propagated through the metabolic network because of the highly connected nature of metabolism.
Keywords: bioinformatics, reporter metabolites, metabolic subnetworks
Linking the genome to its functioning metabolism is of substantial interest not only in studying human diseases (1) but also for identifying metabolic engineering targets in biotechnological applications (2, 3). Transcriptional analysis represents a high-throughput and genome-wide approach for linking the set of expressed genes to functional metabolism of the cell. Indeed, several studies using genome-wide gene-expression analysis have shown that transcriptional regulation plays an important role in regulating metabolism in response to perturbations (4–6). Although many statistical methods and clustering algorithms provide tools to analyze such transcriptomics data (7–9), these methods seldom provide insight into the regulatory architecture of the metabolic networks without intelligent analysis of the results (up/down-regulation of genes of interest or correlation between genes of interest). This shortcoming is primarily due to the hypothesis that there may be all-to-all interactions among the genes being analyzed, resulting into many biologically nonsignificant results. One of the ways to address this problem is to integrate known biological interactions, e.g., protein–protein interactions, in the analysis of transcription data (10). Such an approach essentially reduces the degrees of freedom in data analysis by using knowledge of molecular interactions occurring in the cell. The organization and functioning of the cell can be viewed as a complex network of molecular interactions. These interactions are mediated not only by physical contacts between individual molecules (e.g., protein–protein and protein–DNA interactions) but also result from the functional coupling of certain molecules or groups of molecules (11). Cellular metabolism thus can also be viewed as a network of functional interactions between enzymes and metabolites. This metabolic network represents the channels for the flow of material and generation of Gibbs free energy, which are constrained by the conservation laws of mass and energy. Consequently, we hypothesized that the topology of the interactions involved in metabolism can be used to understand the underlying regulatory mechanisms (e.g., at transcriptional level) controlling this flow of mass and energy. To test this hypothesis, we developed an algorithm that integrates gene-expression data with topological information from genome-scale metabolic models, which enabled systematic identification of so-called reporter metabolites that represent hot spots in terms of metabolic regulation. This study was an attempt to infer the global role of a metabolite based on mRNA-expression patterns and metabolic stoichiometry without direct measurement of metabolite concentration. The algorithm also identifies the significantly correlated metabolic subnetworks after direct or indirect perturbations of the metabolism.
Algorithm
Fig. 1 schematically illustrates the proposed algorithm, which is described step by step in the following.
Fig. 1.
Illustration of the proposed algorithm for identifying reporter metabolites and subnetwork structures signifying transcriptionally regulated modules. A metabolic network (set of reactions) is converted to bipartite (metabolic) and unipartite (enzyme-interaction) graph representations. Gene-expression data from a particular experiment then is used to identify highly regulated metabolites (reporter metabolites) and significantly correlated subnetworks in the enzyme-interaction graph.
Graph-Theoretical Representation of the Metabolic Network. The complete metabolic network in the cell can be represented as a bipartite undirected graph, here referred to as a metabolic graph (Fig. 1) (also see supporting information, which is published on the PNAS web site). In this metabolic graph, metabolites as well as enzymes are represented as nodes, and interactions between them are represented as edges. Thus, a metabolite node is connected to all of the enzyme nodes that catalyze a reaction involving that particular metabolite, and an enzyme node is connected to all of the metabolites that take part in the corresponding reaction. This graph is bipartite, because neither metabolite nor enzyme nodes are directly connected among them.
We also define a unipartite undirected graph, here referred to as an enzyme (or reaction) interaction graph (Fig. 1) (also see supporting information). In this graph, only enzymes are represented as the nodes, and the two enzymes sharing a common substrate in the corresponding reactions are connected to each other. Thus, edges in this graph represent the metabolites shared by two enzymes. Some enzymes catalyze several different reactions, and these enzymes are represented by a single node. This node is linked to all enzyme nodes that are connected to the different reactions carried out by this enzyme.
Mapping and Scoring of Transcription Data. The transcriptional data used in this study can be classified into two categories. The first category includes data in which two different strains (or conditions) are compared and with multiple measurements for each strain (or condition). We refer to this data type as differential data. The second category of data are multidimensional data, e.g., gene expression measured over a time course or with analysis of multiple strains, with or without multiple measurements at the same time point or strain.
Differential data can be mapped on the enzyme nodes of the metabolic or enzyme-interaction graph with a specification of the significance of differential gene expression. Here we used the student's t test to obtain p values, with pi representing the significance of the change for each enzyme. Each pi can subsequently be converted to a Z score of the enzyme node (Zni) by using the inverse normal cumulative distribution (θ–1).
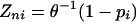
In the case of multidimensional data, the absolute Pearson correlation coefficient, Pj is calculated between all pairs of nodes (enzymes) connected by an edge in the enzyme-interaction graph. The Pj of an edge can be converted to a Z score for that edge (Zej) by using the inverse normal cumulative distribution.
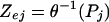
The Z score follows a standard normal distribution for random data, where p values or Pearson coefficients follow a uniform distribution.
Method for Identification of Reporter Metabolites. To identify the reporter metabolites, each metabolite node in the metabolic graph is scored based on the normalized transcriptional response of its neighboring enzymes. In case of differential data, the normalized transcriptional response was calculated as size-independent aggregated Z scores of the k neighboring enzymes.
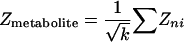
Z_metabolite scores can be corrected for the background distribution by subtracting the mean (μ_k) and dividing by the standard deviation (σ_k_) of the aggregated Z scores of several sets of k enzymes chosen randomly from the metabolic graph.
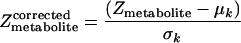
For multidimensional data, the neighboring enzymes of a metabolite in the metabolic graph are represented as an enzyme-interaction graph with all enzymes connected to each other, and hereby Z scores for each edge (Zej) can be calculated as described before. Subsequently, the _Z_metabolite score can be calculated and corrected for the background distribution in the same way as for differential data.
The scoring used for identifying reporter metabolites is basically a test for the null hypothesis, “neighbor enzymes of a metabolite in the metabolic graph show the observed normalized transcriptional response by chance.” The metabolites with the highest score (typically up to 10) are defined as reporter metabolites, and they mark spots in the metabolism, where there is substantial regulation either to maintain homeostasis (i.e., a constant level of the metabolite) or adjust the concentration of the metabolite to another level required for proper functioning of the metabolic network.
Method for Identification of Highly Correlated Subnetworks. As the next step in uncovering the transcriptionally correlated parts of the metabolism after a perturbation, we addressed the problem of identifying highly correlated connected subgraphs (subnetworks) within the enzyme-interaction graph. First we define the score Zs of a connected subnetwork s, which characterizes the biological activity, or the aggregate transcriptional response of the subnetwork as:
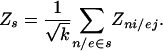
We used the Z score of the node, Zni, in case of differential data and Z score of the edge, Zej, in case of multidimensional data. As in case of the reporter metabolites, we corrected the Zs score for the background distribution of the subnetworks of the same size, randomly sampled from the same network.
Finding the subnetwork with the highest score is a nondeterministic-polynomial-hard problem and was approached by using a simulated annealing algorithm (12) (see supporting information for the details of the implemented algorithm). Within the identified subnetwork, additional subnetworks may be searched by repetition of the algorithm over the subnetwork previously obtained (subnetworks reported in Table 1 was obtained after applying the simulated annealing to larger subnetworks resulting from analysis of the whole metabolic network). We also note that simulated annealing is a stochastic method and does not guarantee that the global optimal solution is found. Moreover, the resulting subnetwork solution might differ depending on the initial conditions and parameters. We addressed these problems by repeating the simulated annealing search several times (≈10) and selecting the subnetwork with the highest score. We observed that it was possible to obtain robust solutions with high scores and biological significance by optimizing the parameters of simulated annealing.
Table 1. Genes included in the subnetworks obtained by analysis of gene-expression data sets for Δ_gdh1_, Δ_grr1_, and carbon sources.
| Data set | Genes |
|---|---|
| Δ_gdh1_ | PFK2, PMP2, PFK1, QNS1, MEP2, GDH1, ADE3, PFK26, HTS1, UGP1, SAM1, BIO3, ERG6, SAH1, PCT1, PRS2, TKL1, TRP5, TPS3, GND1, ALD6, SCS7, BNA1, HOM6, PUR5, YML082W, ASP1, KGD1, LEU4, LSC1, ARG5, MET13, PUT4, UGA4 |
| Δ_grr1_ | HXK1, HXT3, MAL32, STL1, DIP5, YGL186C, TAT2, MUP1, SHM2, ADE3, YER053C, FBP1, ARO2, GLC3, ARO3, ADE6, HIS7, GUA1, RIB1, ACS2, HIS1, PFK2, YDR341C, URA6, ARG1, ADE12, CPA2, PDC5, LEU2, LEU1, MDH3, YAR075W, ADH5, GAD1, ASN2, MET22, SER2, GDH3, PNC1, ILV1, YMR293C, LYS21, LYS20, KGD1, NDI1, RIP1, CYB2, ACH1, XKS1, PGI1, INO1, PGM2 |
| Carbon source | HXK1, HXT2, ACS1, MET22, ARO2, THR4, SER1, GSH1, INM1, TOR1, PRO1, PIK1, PRS2, FUR1, QRI1, LYS20, NAT2, HMGS, HMG1, PAN5, ERG3, YJR078W, ERG11, ERG25, YBR006W, ERG2, CAT2, CIT2, AAT2, BAT2, BAP2, SAM3, BIO2, MDH2, FDH1, GCV1, DFR1, GND2, GND1, PCK1, SOL3, NDH2, YFL030W, ICL1, SFC1, MLS1, ACH1, PGM1 |
Results
We implemented the algorithm for analysis of transcription data from the yeast Saccharomyces cerevisiae. Besides its use as a cell factory, this yeast is used extensively as a model system for studying human diseases (13). We used the recently reconstructed genome-scale metabolic network of S. cerevisiae (14) to generate the metabolic and the reaction–interaction graphs and subsequently applied the algorithm to many yeast gene-expression data sets to illustrate the algorithm.
Deletion of a Gene Encoding an Enzyme. We first analyzed transcription data from a wild-type strain of S. cerevisiae and a mutant with deletion of the gene GDH1, which encodes for NADPH-dependent glutamate dehydrogenase, an enzyme that plays an important role in ammonia assimilation. Physiological analysis of this strain demonstrated an effect on redox metabolism, as observed through increased ethanol yield and decreased glycerol yield (15). However, conventional transcriptome analysis of this mutant, in which differentially expressed genes are identified by using a statistical test (e.g., t test analysis with Bonferroni correction), did not enable identification of the overall effect of this genetic perturbation on the metabolism. Despite these results, using our algorithm we identified several key reporter metabolites, which include: ammonia, glucose 6-phosphate, fructose 6-phosphate, and sedoheptulose 7-phosphate (Table 2). The fact that ammonia (both intracellular and extracellular ammonia) is identified as a reporter metabolite is biologically reasonable, because ammonia assimilation has been altered. It may intuitively be more difficult to understand why the three sugar phosphates appear as reporter metabolites. However, these three metabolites represent branch points between the Embden–Meyerhof–Parnas and pentose-phosphate pathways. After deletion of GDH1, the requirement for NADPH in connection with cellular growth is reduced by >40% (16), which reduces the requirement for shunting glucose through the pentose-phosphate pathway, which acts as the primary source for NADPH in S. cerevisiae.
Table 2. Reporter metabolites for Δ_gdh1_, Δ_grr1_, and carbon source data sets.
| Metabolite | No. of neighbors | No. of KEGG pathways |
|---|---|---|
| Δ_gdh1_ | ||
| Fructose 6-phosphate | 15 | 5 |
| Glucose 6-phosphate | 11 | 6 |
| NH3xt | 3 | — |
| NH3 | 32 | 7 |
| GABAxt | 2 | — |
| CTP | 8 | 1 |
| Fructose 1,6-bisphosphate | 4 | 4 |
| Sedoheptulose 7-phosphate | 5 | 2 |
| CO2M | 12 | — |
| _N_-Acetyl-l-glutamate 5-semialdehydeM | 2 | — |
| Δ_grr1_ | ||
| l-Glutamine | 20 | 5 |
| Glucose-xt | 14 | — |
| Mannose | 15 | 2 |
| Fructose | 14 | 3 |
| Fructose-xt | 12 | — |
| Glycogen | 4 | — |
| Orthophosphate | 65 | 3 |
| Glucose | 28 | 6 |
| Mannose-xt | 11 | — |
| Homocitric acid | 2 | 2 |
| Carbon source | ||
| Maltose | 4 | 1 |
| Carnitine | 3 | 1 |
| (R)-Pantoate | 2 | 1 |
| Glyoxylate | 6 | 5 |
| 6-phospho-gluconate | 5 | 1 |
| Episterol | 2 | — |
| 3-Demethylubiquinone-9M | 2 | — |
| H+EXT | 42 | — |
| 3-Phosphonooxypyruvate | 3 | 1 |
| 1-Phosphatidyl-1-d-_myo_-inositol 4-phosphate | 4 | 2 |
Looking at the highly correlated metabolic subnetwork, we found the high-scoring subnetwork to consist of 181 genes distributed in 68 Munich Information Center for Protein Sequences (MIPS) functional categories (17) (supporting information), of which 31% belong to MIPS functional categories amino acid metabolism and transport, carbohydrate utilization, and nucleotide metabolism. Additional analysis of the 181-gene subnetwork resulted in identification of a 34-gene subnetwork (Table 1). This subnetwork consists of 10 genes (apart from GDH1) encoding enzymes catalyzing oxidoreductive reactions involving the cofactors NADPH/NADH, clearly demonstrating the effect of GDH1 deletion on redox metabolism. In fact, these cofactors represent the main links in this subnetwork, which involves two key nodes in the cellular metabolism (Fig. 2): (i) the node between the Embden–Meyerhof–Parnas pathway and the pentose-phosphate pathway and (ii) the node around α-ketoglutarate. The first node is known to be controlled by the requirement for NADPH. The decrease in expression of genes of the pentose-phosphate pathway is consistent with a decreased flux through this pathway in a similar mutant (18). The second node is directly perturbed, and it makes sense that this change results in a transcriptional response of enzymes around this node. It has indeed been shown that in a Δ_gdh1_ mutant, the level of α-ketoglutarate is increased (19), which is consistent with a decreased expression of the genes KGD and LSC, both encoding enzymes downstream of α-ketoglutarate.
Fig. 2.
Parts of S. cerevisiae metabolism that are represented in the subnetwork identified for the Δ_gdh1_ data set. Genes present in the subnetwork are shown in boxes.
Deletion of a Gene Encoding a Regulatory Protein. To further evaluate the method, we also analyzed transcription data from a Δ_grr1_ mutant of S. cerevisiae compared with a wild-type strain, both grown at high glucose concentrations (20). Grr1p is a ubiquitin-protein ligase that plays a role in glucose repression (21). Overall, it is known that Grr1p deactivates the Rgt1p transcriptional repression of several hexose transporters, and the important role of Grr1p in regulating sugar transporters is clearly seen from the list of reporter metabolites identified in this case (Table 2). Among the 10 most important reporter metabolites, six are hexoses, all transported by the group of HXT genes in S. cerevisiae. The other reporter metabolites include glutamine, orthophosphate, and glycogen. Glutamine plays a key role in the nitrogen metabolism, which is normally considered also to be regulated by Grr1p, although a direct link has not been established (22). Orthophosphate is involved in a large number of reactions in the central carbon metabolism, and the identification of this reporter metabolite is a clear indication of the multitude of effects caused by deletion of GRR1. In the Δ_grr1_ mutant, a high-scoring metabolic subnetwork of 204 genes was identified, and additional analysis of this network resulted in identification of a 52-gene subnetwork (Table 1). Besides several genes encoding sugar and amino acid transporters that are known to be regulated by Grr1p, this subnetwork also contains many other genes involved in amino acid metabolism.
Multidimensional Data. To illustrate the application of the method for analysis of transcription data measured over several different environmental conditions, we analyzed transcription data for S. cerevisiae grown on four different carbon sources, glucose (a hexose), maltose (a disaccharide), and two C-2 compounds, ethanol and acetate (23). For analysis of this type of data set, it is intuitively more difficult to interpret the results in terms of the changes in physiology, because the data span a multidimensional space. However, the reporter metabolites (Table 2) still reflect the metabolic reprogramming in response to the changes in carbon source. Maltose is an obvious reporter metabolite, because enzymes involved in uptake and metabolism of this sugar are induced only in the presence of maltose. The presence of glyoxylate and carnitine as reporter metabolites is due to the key roles of these metabolites during growth on C-2 compounds (24). Appearance of H+ as a reporter metabolite illustrates the ability of the algorithm to identify metabolites indirectly involved in metabolism, because transport of maltose and acetate is coupled with proton transport across the cell membrane. We also performed a pairwise comparison of the four carbon sources, and the results are provided in the supporting information.
Large-Scale Reporter Metabolite Analysis. To further evaluate the algorithm, we performed reporter metabolite analysis of 47 transcriptional data sets (see supporting information). In all these cases, reporter metabolites provided useful information about the metabolic changes underlying the particular experiment, e.g., the reporter metabolites identified for the comparison of carbon- and nitrogen-limited conditions clearly show the underlying metabolic changes in major pathways for utilization of these substrates. We also found that relatively few metabolites were identified as reporter metabolites for many of the conditions analyzed, which is due to the fact that similar types of perturbations are introduced in many of these studies (e.g., change in substrate, comparison between aerobic and anaerobic conditions). Nevertheless, it is interesting to note that one third of all the metabolites in the metabolic graph were identified as a reporter metabolite in at least one of the studies (see supporting information for the complete distribution). Moreover, the average rank of any metabolite (defined as arithmetic average of ranks of a metabolite, based on _Z_metabolite score, from all conditions analyzed) was found to be >150, further illustrating the uniqueness of reporter metabolites for the particular experiment.
Discussion
Reporter metabolites and corresponding subnetworks from all three cases, representing three different types of perturbations (namely deletion of a gene-encoding enzyme, deletion of a gene-encoding regulatory protein, and change in environment of a cell) clearly project the metabolic changes after these perturbations. Because the transcriptional changes at individual gene levels are small, they are not identified by using conventional statistical significance tests or clustering methods (see supporting information), whereas our hypothesis-driven analysis of transcription data enables identification of small and coordinated changes in expression levels. We also note that several of the identified reporter metabolites are involved in a relatively large number of reactions (Table 2) that are distributed in several different Kyoto Encyclopedia of Genes and Genomes (KEGG) (25) pathways. Thus, mapping of transcriptional changes onto KEGG pathways, as is often done for visual representation of the transcriptional changes, may be misleading.
The metabolic graph of S. cerevisiae consists of 2,000 nodes (825 metabolites and 1,175 reactions) and 4,196 edges, whereas the reaction–interaction graph has 1,175 nodes and 57,217 edges. Notably, a large fraction of these edges represents interactions caused by energy and redox cofactors giving highly connected graphs (the average path length between any two nodes is 5.17 and 2.49 for the metabolic and reaction–interaction graphs, respectively) with “small-world properties” (26, 27). The high degree of connectivity of the metabolic network implies that the disturbance at any node in the network can affect all branches of the metabolism and hence demands a global control, which can be seen from the subnetwork analysis in which we found large significant subnetworks spanning all branches of the metabolism (supporting information). Such changes, however, are centered on the perturbed node (/s), as can be seen from the reporter metabolite analysis that identifies such nodes in the metabolism.
Because of the high connectivity of the metabolic network, the here-reported algorithm is found to be quite robust to alterations in the metabolic graph (e.g., removal of certain metabolites). To evaluate this robustness, we removed some of the highly connected cofactors from the graph and studied the effect on the network connectivity and subnetworks obtained for the GDH1 data set (see supporting information). It was possible to obtain ≈75% overlap with the original subnetwork even after the removal of both redox cofactors (NAD+/NADH and NADP+/NADPH) and an ATP/ADP pair, which resulted in 27% reduction in the number of edges. The result was most sensitive to the removal of NADP+/NADPH, which is consistent with the fact that GDH1 encodes for a NADPH-dependent enzyme. It is notable that the removal of NAD+/NADH did not influence the results significantly, although it resulted in a substantial decrease in the number of edges in the network
Although the regulatory network structure defines the details of how the transcriptional regulatory program is executed, the metabolic network itself seems to guide this machinery, which we see as the consequence of the fact that metabolic regulation has been designed and evolved for and around the metabolites. We exploited this hypothesis by developing an effective algorithm that enables understanding the transcriptional changes of the metabolism after genetic and environmental perturbations. Apart from uncovering the architecture of the transcriptional changes after known perturbations, our approach will be useful also in identifying the effects of unknown or poorly characterized disturbances, e.g., deletion of an ORF with unknown function or exposure to a drug, and hereby provide clues to the role of the ORF or the drug on the cellular metabolism.
Supplementary Material
Supporting Information
Acknowledgments
We are grateful to I. Rocha and M. Åkesson for fruitful discussions. We also thank J. Villadsen, M. Hjortsø, G. Lettier, A. P. Oliveira, T. Grotkjær, and M. Jewett for helpful suggestions.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviation: KEGG, Kyoto Encyclopedia of Genes and Genomes.
References
- 1.Peltonen, L. & McKusick, V. A. (2001) Science 291**,** 1224–1229. [DOI] [PubMed] [Google Scholar]
- 2.Patil, K. R., Akesson, M. & Nielsen, J. (2004) Curr. Opin. Biotechnol. 15**,** 64–69. [DOI] [PubMed] [Google Scholar]
- 3.Nielsen, J. & Olsson, L. (2002) FEMS Yeast Res. 2**,** 175–181. [DOI] [PubMed] [Google Scholar]
- 4.Ihmels, J., Levy, R. & Barkai, N. (2004) Nat. Biotechnol. 22**,** 86–92. [DOI] [PubMed] [Google Scholar]
- 5.DeRisi, J. L., Iyer, V. R. & Brown, P. O. (1997) Science 278**,** 680–686. [DOI] [PubMed] [Google Scholar]
- 6.Miki, R., Kadota, K., Bono, H., Mizuno, Y., Tomaru, Y., Carninci, P., Itoh, M., Shibata, K., Kawai, J., Konno, H., et al. (2001) Proc. Natl. Acad. Sci. USA 98**,** 2199–2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eisen, M. B., Spellman, P. T., Brown, P. O. & Botstein, D. (1998) Proc. Natl. Acad. Sci. USA 95**,** 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Herrero, J., Vaquerizas, J. M., Al-Shahrour, F., Conde, L., Mateos, A., Diaz-Uriarte, J. S. R. & Dopazo, J. (2004) Nucleic Acids Res. 32**,** W485–W491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sherlock, G. (2000) Curr. Opin. Immunol. 12**,** 201–205. [DOI] [PubMed] [Google Scholar]
- 10.Ideker, T., Thorsson, V., Ranish, J. A., Christmas, R., Buhler, J., Eng, J. K., Bumgarner, R., Goodlett, D. R., Aebersold, R. & Hood, L. (2001) Science 292**,** 929–934. [DOI] [PubMed] [Google Scholar]
- 11.Lee, I., Date, S. V., Adai, A. T. & Marcotte, E. M. (2004) Science 306**,** 1555–1558. [DOI] [PubMed] [Google Scholar]
- 12.Ideker, T., Ozier, O., Schwikowski, B. & Siegel, A. F. (2002) Bioinformatics 18**,** 233S–240S. [DOI] [PubMed] [Google Scholar]
- 13.Botstein, D., Chervitz, S. A. & Cherry, J. M. (1997) Science 277**,** 1259–1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Forster, J., Famili, I., Fu, P., Palsson, B. O. & Nielsen, J. (2003) Genome Res. 13**,** 244–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bro, C., Regenberg, B. & Nielsen, J. (2004) Biotechnol. Bioeng. 85**,** 269–276. [DOI] [PubMed] [Google Scholar]
- 16.Nissen, T. L., Kielland-Brandt, M. C., Nielsen, J. & Villadsen, J. (2000) Metab. Eng. 2**,** 69–77. [DOI] [PubMed] [Google Scholar]
- 17.Mewes, H. W., Amid, C., Arnold, R., Frishman, D., Guldener, U., Mannhaupt, G., Munsterkotter, M., Pagel, P., Strack, N., Stumpflen, V., et al. (2004) Nucleic Acids Res. 32**,** D41–D44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Moreira dos, S. M., Thygesen, G., Kotter, P., Olsson, L. & Nielsen, J. (2003) FEMS Yeast Res. 4**,** 59–68. [DOI] [PubMed] [Google Scholar]
- 19.DeLuna, A., Avendano, A., Riego, L. & Gonzalez, A. (2001) J. Biol. Chem. 276**,** 43775–43783. [DOI] [PubMed] [Google Scholar]
- 20.Westergaard, S. L., Bro, C., Olsson, L. & Nielsen, J. (2004) FEMS Yeast Res. 5**,** 193–204. [DOI] [PubMed] [Google Scholar]
- 21.Flick, K. M., Spielewoy, N., Kalashnikova, T. I., Guaderrama, M., Zhu, Q., Chang, H. C. & Wittenberg, C. (2003) Mol. Biol. Cell 14**,** 3230–3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bernard, F. & Andre, B. (2001) FEBS Lett. 496**,** 81–85. [DOI] [PubMed] [Google Scholar]
- 23.Daran-Lapujade, P., Jansen, M. L. A., Daran, J. M., van Gulik, W., de Winde, J. H. & Pronk, J. T. (2004) J. Biol. Chem. 279**,** 9125–9138. [DOI] [PubMed] [Google Scholar]
- 24.Gancedo, J. M. & Gancedo, C. (1997) in Yeast Sugar Metabolism: Biochemistry, Genetics, Biotechnology, and Applications, eds. Zimeermann, F. K. & Entian, K. D. (Technomic, Lancaster, PA), pp. 359–377.
- 25.Kanehisa, M., Goto, S., Kawashima, S., Okuno, Y. & Hattori, M. (2004) Nucleic Acids Res. 32**,** D277–D280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fell, D. A. & Wagner, A. (2000) Nat. Biotechnol. 18**,** 1121–1122. [DOI] [PubMed] [Google Scholar]
- 27.Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N. & Barabasi, A. L. (2000) Nature 407**,** 651–654. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information

