Rates of intron loss and gain: Implications for early eukaryotic evolution (original) (raw)

Abstract

We study the intron–exon structures of 684 groups of orthologs from seven diverse eukaryotic genomes and provide maximum likelihood estimates for rates and numbers of intron losses and gains in these same genes for a variety of lineages. Rates of intron loss vary from ≈2 × 10–9 to 2 × 10–10 per year. Rates of gain vary from 6 × 10–13 to 4 × 10–12 per possible intron insertion site per year. There is an inverse correspondence between rates of intron loss and gain, leading to a 20-fold variation among lineages in the ratio of the rates of the two processes. The observed rates of intron gain are insufficient to explain the large number of introns estimated to have been present in the plant–animal ancestor, suggesting that introns present in early eukaryotes may have been created by a fundamentally different process than more recently gained introns.

Keywords: genome evolution

The debate over the relative importance of intron loss and gain in shaping the pattern of imperfect conservation of intron–exon structures between homologues has been long and hard fought (1–51). For the first 25 years, the debate was waged in the context of the introns-early/introns-late question. Proponents of introns-late believe that spliceosomal introns are relatively recent arrivals whose modern restriction to eukaryotes reflects their absence in the common ancestors of prokaryotes and eukaryotes and subsequent origin within eukaryotes (1, 12, 24, 37, 52–56). Their task was thus to demonstrate that modern intron–exon structures could be explained primarily or solely by intron gain in eukaryotes, without a necessarily major role for intron loss. Introns-early adherents believe that introns are primordial structures whose presence in eukaryote–prokaryote ancestors facilitated the construction of early genes (2–11, 15, 22, 23, 25, 33, 35, 40). The presence of large numbers of introns in modern genomes thus does not necessarily require active intron insertion in eukaryotes, although the lack of spliceosomal introns in prokaryotes, as well as the existence of some introns with spotty phylogenetic distributions within eukaryotes, require significant intron loss. In this way was the more fundamental debate about the timing of origin of the first spliceosomal introns, with all its implications for the origins of early genes, the emergence of complex genomes, and the divergence of the three kingdoms of life, projected onto the issue of intron loss and gain. Since that time, both perspectives have been softened, intronsearly by discoveries of introns whose very limited phylogenetic distributions suggest their recent gain (3, 7–12, 20, 22, 33, 42–44) and introns-late by the discovery of introns and spliceosomal components in very deep-branching eukaryotes (57–60). However, the basic disagreements over when spliceosomal introns first appeared in significant numbers and whether eukaryotic evolution has been characterized by generally decreasing, stable, or increasing intron density persist (30–50).

In the first characterized case of intron discordance, Perler et al. (1) found that an intron specific to one of a pair of recent insulin duplicates in rat is shared with chicken, demonstrating intron loss. The next two decades brought cases of intron loss and gain in steadily increasing streams (3, 4, 7–14, 17–22, 28, 29, 33), although the largely anecdotal nature of these early studies prevented firm general conclusions about the relative importance of the two processes. With the genomic age came more comprehensive surveys. Studies of large numbers of ortholog pairs described extents and patterns of intron conservation and showed much variation across groups, with >90% intron conservation between humans and fish (20, 61), whereas more recently diverged pairs of dipteran, Caenorhabditis, and Plasmodium species showed far more differences (62, 63). At a deeper level, as many as 25–33% of intron positions are shared between multiple eukaryotic kingdoms (34, 64). Other studies have analyzed the causes of such differences (intron loss or gain). One uncovered a mere five losses and no gains in 1,576 human–mouse–pufferfish ortholog trios (36), and another found roughly balanced intron losses and gains in four species of euascomyces fungi (49). Studies of intron–exon structures in large paralogous gene families from one or a few organisms (3, 14, 16–18, 21, 22, 28, 31, 47) or from large amounts of available sequence (6, 10, 39, 40) tended to conclude that intron evolution was a mixed bag, with some lineages dominated by intron loss, others by gain.

In the most extensive study of intron–exon structure in orthologs, Rogozin et al. (34) used Dollo parsimony to reconstruct the history of 684 sets of orthologs from eight eukaryotic species. They presented a varied picture of intron evolution, with some lineages experiencing sharp reductions in intron number, and others seeing sharp increases. In a previous publication, we argued that parsimony is not appropriate for such reconstructions because it fails to recover ancestral introns in cases of loss (50). A maximum likelihood analysis of their data showed a different picture, with generally intron-rich eukaryotic ancestors and net intron losses in most branches: 6 of 10 studied branches experienced a significant net loss, and 2 showed a net gain (50).

We extend that analysis here. Previously, we estimated only net changes in intron number in the studied regions (e.g., there are 3,345 introns in these regions in humans versus an estimated 3,321 in the bilateran ancestor, thus a change of +24). We here provide individual estimates for numbers of losses and gains for each branch (976 gains and 952 losses along the same branch). We find significant variations in rates of intron loss and gain between branches. Rates of intron loss range from ≈2 × 10–10 to 2 × 10–9 per year, whereas rates of intron gain per possible insertion site are orders of magnitude smaller, from ≈6 × 10–13 to 4 × 10–12. There is an inverse relationship between rates of the two processes. The estimated rates suggest that early eukaryotic ancestors predating even the plant–animal split were very intron-rich and that introns in early eukaryotes may have arisen by qualitatively different processes than more recent insertions.

Methods

Data Set and Programs. We downloaded amino acid level alignments and corresponding intron positions for 684 clusters of orthologous genes from eight eukaryotic species, compiled and previously studied by Rogozin et al. (34). Only intron positions in conserved regions were considered (see ref. 34 for details). Introns at the exact same position (between the exact corresponding pair of nucleotides in the alignment) in different species were assumed homologous and not due to independent multiple insertions, an assumption supported by independent evidence (ref. 46; discussed in ref. 50). Only introns present at the exact same position were considered homologous (34). Saccharomyces cerevisiae was excluded because of its dearth of introns. We wrote Perl programs to perform the analyses described.

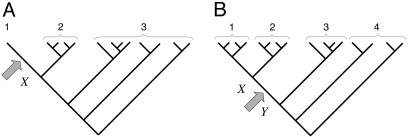
Estimates of Numbers of Intron Losses and Gains. External branches. Fig. 1_A_ depicts a scenario in which species 1 diverges from (a group of) species 2 at node X with (a group of) outgroups 3. We call the probabilities that an intron present in ancestor X is present in species 1, in some species from group 2, and in some species from group 3: _o_1, _o_2, and _o_3, respectively. An intron present in ancestor X will have one of the following six modern phylogenetic distributions with respect to species 1 and groups 2 and 3, with probabilities: (i) Pr{present in 1, 2, and 3|present in X} = _o_1_o_2_o_3; (ii) Pr{present in 1 and 2; absent in 3|X} = _o_1_o_2(1–_o_3); (iii) Pr{present in 1 and 3; absent in 2|X} = _o_1(1–_o_2)_o_3; (iv) Pr{present in 2 and 3; absent in 1|X} = (1–_o_1)_o_2_o_3; (v) Pr{present in 1; absent in 2 and 3|X} = _o_1(1–_o_2)(1–_o_3); and (vi) Pr{absent in 1; present in 2 or 3 or neither|X} = (1–_o_1)(1–_o_2_o_3). The total number of introns present in X but lost along the branch leading from X to 1, which we call l, is equal to the number in categories iv and vi. Introns found only in species 1 are either gained since X or present in X but absent in 2 and 3 (category v); the number gained along the branch from X to 1, which we call g, is thus the total number found only in species 1 minus the number in category v. The conditional probability of seeing the data is:

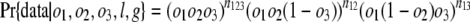graphic file with name M1.gif [1]

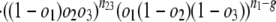
graphic file with name M2.gif

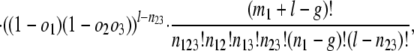
graphic file with name M3.gif

where n values give numbers of introns present in exactly the indicated groups [e.g., _n_123 is the number present in species 1 and (some species from) each of groups 2 and 3, _n_12 the number present in 1 and 2 but not 3]; and m values give numbers of introns present in at least the indicated groups (e.g., _m_1 is the number of all introns present in group 1, regardless of presence elsewhere: _m_1 = _n_123 + _n_12 + _n_13 + _n_1). The likelihood of a set of parameters is then L{_o_1, _o_2, _o_3, l, g} = Pr{data|_o_1, _o_2, _o_3, l, g} with maximum likelihood estimates (MLE) at

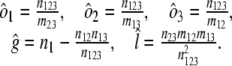graphic file with name M4.gif [2]

Confidence intervals for l, g, and _o_1 were derived by using the profile likelihood method, which treats all parameters except one as nuisance parameters and maximizes over them (67, 68).

Fig. 1.

Fig. 1.

General phylogenies for demonstrating the method. (A) External branch. (B) Internal branch. Arrows indicate the branches analyzed.

Internal branches. Fig. 1_b_ depicts the scenario for an internal branch. Here we define _o_1 = Pr{1|X}, _o_2 = Pr{2|X}, _o_3 = Pr{3|Y}, _o_4 = Pr{4|Y}, and r = Pr{X|Y}, where for instance Pr{1|X} is the probability that an intron is present in some species in group 1 given that it is present in ancestor X, and Pr{X|Y} is the probability that an intron present in ancestor Y is retained in ancestor X.

Table 1 gives all possible histories of an intron present in Y. To estimate numbers of Y-X branch losses, alternative histories leading to identical modern phylogenetic patterns are treated separately: for instance, both x and xi lead to presence in 3 and 4 and absence in 1 and 2, but xi includes loss along the Y-X branch, whereas x includes retention along the Y-X branch, followed by independent loss in 1 and 2.

Table 1. Possible histories of introns.

graphic file with name 5774_f01.jpg

n and m values (except nX) are known values similar to those above (e.g., _n_124 is the number of introns present in 1, 2, and 4, but not 3; _m_124 = _n_124 + _n_1234). _l, g, l_34, and nX are unknown quantities to be estimated: l and g are the total number of introns lost and gained along the Y-X branch, respectively, _l_34 is the number present in both 3 and 4 but lost along the Y-X branch, and nX is the number present in X but absent in 3 and 4. g is thus nX minus the number of introns present in Y, retained in X, and absent in 3 and 4 (xii_–_xv). Introns with histories xvi and xvii are neither gained or lost along the Y-X branch nor directly observable as ancestrally present and are thus uninformative and ignored. For each of the nX introns present in X but absent in 3 and 4, Table 2 gives the possible subsequent histories.

Table 2.

Possible histories and modern phylogenetic distributions for an intron present in ancestor X but absent in groups 3 and 4

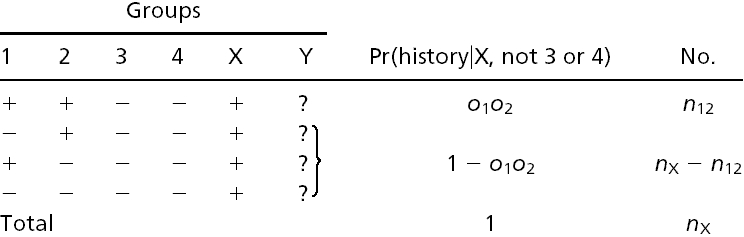
graphic file with name 5775_f01.jpg

The conditional probability of seeing the data simplifies to:

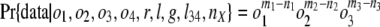graphic file with name M5.gif [3]

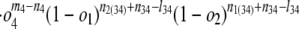
graphic file with name M6.gif

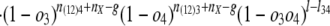
graphic file with name M7.gif

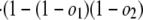
graphic file with name M8.gif

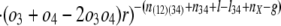
graphic file with name M9.gif

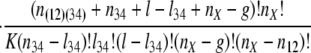
graphic file with name M10.gif

where K is the product of the factorials of several known n values (see Supporting Text, which is published as supporting information on the PNAS web site). The likelihood of a set of parameters is then L{_o_1, _o_2, _o_3, _o_4, _r, l, g, l_34, nX} = Pr{data|_o_1, _o_2, _o_3, _o_4, _r, l, g, l_34, nX}, which has its MLE at

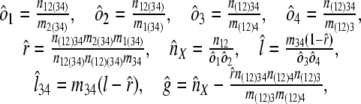graphic file with name M11.gif [4]

where parentheses indicate that an intron must be present in at least one of the parenthesized groups to be counted (e.g., n(12)3 = _n_13 + _n_23 + _n_123; m(12)3 = _n_13 + _n_134 + _n_23 + _n_234 + _n_123 + _n_1234).

Introns Gained and Subsequently Lost Along the Same Branch. For each branch, the estimated g includes only gained introns that survive to the end of the branch; the estimated l includes only introns present at the beginning of the branch and then lost. Both values exclude introns that are gained and then lost along the same branch. As such, g and l underestimate the real numbers of introns gained and lost along the branch (call them _g_′ and _l_′, respectively).

If introns are lost at constant rate along the branch and a total fraction 1 – x of introns present at the beginning of a branch are lost before the end of that branch, an intron gained at a fraction f of the way along the length of the branch has an x_1–_f chance of being retained until the end of the branch. If intron gains also occur at constant rate along the branch, then

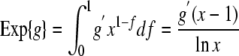graphic file with name M12.gif [5]

For each external and internal branch, we used the MLE of g and x (equals _ô_1 for external branches and_r̂_for internal branches) to give estimates for _g_′, and then simply _l_′ = l + _g_′ – g.

Rates of Intron Gain and Loss. For each branch, the estimated number of intron gains in the studied regions per year is simply the estimated g_′ divided by T, the estimated branch length in years. The rate per site is then simply the rate for the whole region divided by the total number of possible insertion sites (488,157) in the region. The estimated yearly rate of loss is d = 1 – x_1/T.

Intron Number in the _Plasmodium_-Crown Ancestor. The MLE for the probability that an intron present in the animal–plant (crown) ancestor is retained in Arabidopsis thaliana is 0.61, and the MLE for the probability it is retained in Schizosaccharomyces pombe and/or an animal is 0.75 (because 73 of 97 introns present in Arabidopsis thaliana and Plasmodium falciparum are present in S. pombe and/or an animal), so the chance that an intron present in the crown ancestor is found in some modern descendent is 1 – (1–0.75) × (1–0.61) = 0.90.

Postulating a rate of intron loss per year d for the deepest branches of the tree and divergence times of t_1 and t_2 years for the plant–animal and crown–apicomplexan divergences, respectively, the probability that an intron present in the ancestor is retained in P. falciparum and some modern crown descendent is 0.9(1–_d)2_t_2–_t_1. The observed 143 introns shared between P. falciparum and crown group taxa thus suggest some 143/[0.9(1–_d)2_t_2–_t_1] total introns present in the common ancestor.

Results

Data Set. We studied the intron–exon structures of conserved regions of 684 sets of orthologs from seven eukaryotic species. For each set of orthologs, intron positions are mapped onto the protein sequence, and the protein sequences aligned, giving numbers of intron positions shared between any group (pair, trio, etc.) of species. The data are summarized in Tables 3 and 4. An earlier study used Dollo parsimony to reconstruct the history of intron gains and losses in this data set (34). Such a reconstruction is provided in Fig. 2 for comparison.

Table 3. Summary of the data used in estimating intron losses and gains along external branches.

Introns shared exclusively between groups
Branch Species 1 Group 2 1 2 3 1-2 1-3 2-3 1-2-3
D. melanogaster D. melanogaster A. gambiae 147 137 6,204 87 194 156 295
A. gambiae A. gambiae D. melanogaster 137 147 6,204 87 156 194 295
C. elegans C. elegans Diptera 798 371 4,970 36 436 411 198
H. sapiens H. sapiens Ecdysozoan 1,844 1,205 2,558 594 568 112 339
S. pombe S. pombe Bilateran 200 3,643 2,331 92 27 796 131
A. thaliana A. thaliana Opisthokont 2,001 3,935 306 835 24 46 73

Table 4. Summary of the data used in estimating the numbers of intron losses and gains along internal branches.

Group Introns shared exclusively between groups
Branch 1 2 3 1 2 3 4 1-2 1-3 2-3 1-4 2-4 3-4 1-2-3 1-2-4 1-3-4 2-3-4 1-2-3-4
Ecdysozoan-Diptera D. melanogaster A. gambiae C. elegans 147 137 798 4,970 87 13 10 136 101 436 13 174 45 45 108
Bilateran-Ecdysozoan Diptera C. elegans H. sapiens 371 798 1,844 2,558 36 244 246 35 71 568 104 6 132 119 88
Opisthokont-Bilateran Ecdysozoan H. sapiens S. pombe 1,205 1,844 200 2,331 594 11 46 96 463 27 35 237 5 59 67
Crown-Opisthokont Bilateran S. pombe A. thaliana 3,643 200 2,001 306 92 711 24 35 1 24 100 10 50 2 21

Fig. 2.

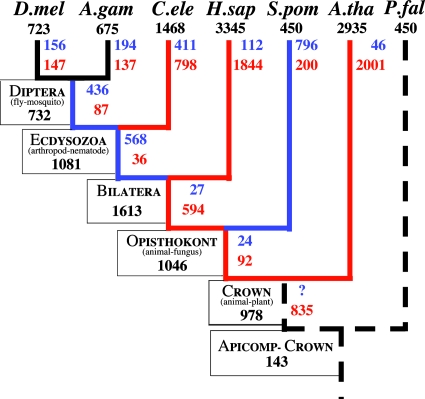
Fig. 2.

A Dollo parsimony reconstruction of the data for comparison with our results.

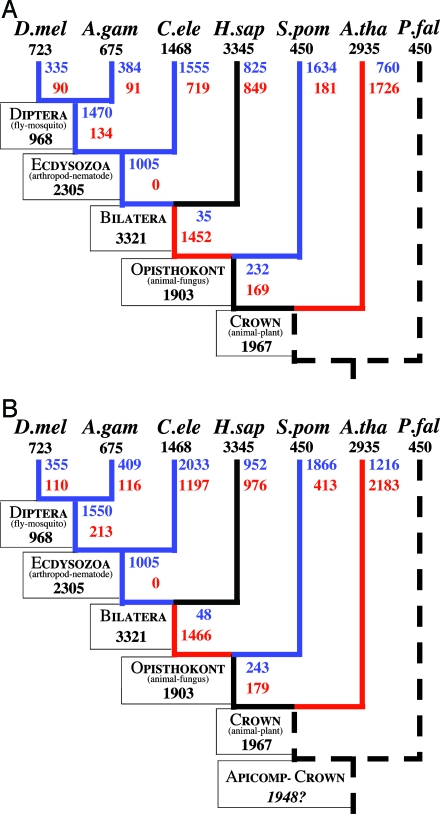
Numbers of Intron Losses and Gains. We used the pattern of intron conservation in the conserved regions of 684 groups of orthologs from seven eukaryotic species to calculate MLE for numbers of intron gains and losses in these genes along each branch of the tree. The estimates are shown in Fig. 3_A_ with confidence intervals given in Fig. 4, which is published as supporting information on the PNAS web site. These estimates exclude introns gained and then lost along the same branch. Assuming constant rates of intron loss and gain along the length of each branch, we corrected our estimates for such introns (Fig. 3_B_).

Fig. 3.

Fig. 3.

MLE of the numbers of intron losses and gains for 684 groups of orthologs. Number of introns present in modern species or previously estimated present in ancestors (50) are given in black. MLE of the number of intron losses and gains along each branch are given in blue and red, respectively. Blue branches are inferred to have experienced >1.5 losses per gain; red branches >1.5 gains per loss. (A) Initial estimates, excluding introns that are gained and subsequently lost along the same branch. (B) Final results, correcting for introns that are gained and subsequently lost along the same branch. The estimate of the number of introns present in the studied regions in the Plasmodium crown ancestor is derived assuming that the deepest branches had an average rate of loss (see Discussion).

Overall Probabilities of Loss and Rates of Intron Loss and Gain. We calculated MLE for the fraction of introns lost along each external branch (Table 5; confidence intervals in Fig. 5, which is published as supporting information on the PNAS web site). Given estimates of the length of each external branch, we then estimated yearly rates of loss of existent introns and of insertion of new introns per possible insertion site (adjacent pair of nucleotides) (Table 5).

Table 5. Estimates of intron loss and gain for external branches.

Number Rate
Branch Length, MY Losses (%) Gains Ratio Loss × 10-9 Gain × 10-12 Ratio
D. melanogaster 250-300 355 (35) 110 3.2 1.4-2.0 0.7-0.9 1,958
A. gambiae 250-300 409 (40) 116 3.5 1.7-2.2 0.8-0.9 2,202
C. elegans 500-700 2,033 (67) 1,197 1.7 1.6-2.2 3.4-4.8 463
H. sapiens 600-800 952 (25) 976 1.0 0.4-0.5 2.4-3.3 147
S. pombe 1,000-1,500 1,866 (86) 413 4.5 1.3-2.0 0.6-0.8 2,380
A. thaliana 1,500-2,000 1,216 (39) 2,183 0.6 0.2-0.3 2.2-2.9 113

Discussion

We provide MLE for the numbers and rates of intron gain and loss in 684 sets of orthologs over a variety of eukaryotic lineages. These results show significant variations between lineages in rates of both intron loss and gain and in relative rates of the two processes. Rates of intron loss along external branches vary ≈10-fold, from ≈2 × 10–10 to 2 × 10–9. Rates of gain are orders of magnitude smaller, at 6 × 10–13 to 4 × 10–12 per year per possible insertion site (pair of adjacent nucleotides).

Ratios of the rates of the two processes also vary considerably between lineages. Among external branches, ratios of the rates of intron loss and gain vary 20-fold from 113 up to 2,380; ratios of the total numbers of intron losses to gains vary 10-fold from one-half to five. There is an inverse correspondence across branches between rates of intron gain and intron loss: some branches have high rates of loss and low rates of gain (Drosophila melanogaster, Anopheles gambiae, and S. pombe); others have high rates of gain and low rates of loss (H. sapiens and Arabidopsis thaliana). This pattern is not predicted by a purely neutral model of intron evolution but is instead suggestive of differential intensity or efficiency (because of differences in population size) of selection across lineages. The sole exception to this pattern is the branch running from the ecdysozoan ancestor to C. elegans, which shows high rates of both intron loss and gain. This observation joins a host of other differences in intron evolution between nematodes and other groups, with nematodes showing unusually strict splice junction consensus sequences (discussed in ref. 43) as well as a lack of a suite of otherwise general biases in the pattern of intron loss (51).

In contrast to the pattern seen among external branches, two of the internal branches show extremely skewed patterns, with the bilateran–ecdysozoan branch showing 1,005 intron losses but no intron gains and the opisthokont–bilateran branch showing 1,466 gains and only 48 losses. These aberrant patterns are most likely due to unaccounted for differences in loss rates between introns along the same branch. Such differences cause systematic underestimation of intron losses and overestimation of intron gains on external branches (thus our finding of an excess of intron loss is conservative); the pattern is not so predictable for internal branches (unpublished data). Future work should explore the effects of such interintron rate differences on intron loss and gain estimates for internal branches.

Comparison with Parsimony. Our results stand in contrast to those of Rogozin et al. (34), who used Dollo parsimony to reconstruct the history of intron gain and loss in this same data set. Such a reconstruction is given in Fig. 2. Comparison of Figs. 2 and 3 shows consistent differences in the estimates of numbers of intron losses and gains between the two methods, with parsimony generally favoring intron gain over intron loss. Whereas parsimony infers that 5 studied branches of 10 experienced at least 50% more intron gains than losses, maximum likelihood shows only 2 such branches. On the other hand, parsimony infers that only three branches have experienced 50% more losses than gains, whereas maximum likelihood shows six. Parsimony suggests that the bilateran–human branch has experienced 17 gains for each loss, whereas maximum likelihood shows equal numbers of gains and losses; parsimony shows two gains per loss in the ecdyosozoan–C. elegans branch versus maximum likelihood's two losses per gain. These differences are caused by the failure of parsimony to estimate intron losses that are not directly observed, leading to an overemphasis of intron gain.

Early Eukaryotic Evolution. The external branches studied show 0.3 to 2 intron gains in the studied regions per million years. We previously estimated that the common ancestor of animals and plants harbored some 2,000 introns in these regions (50). If even earlier ancestors had accumulated 0.3 introns per year, nearly 7 billion years of constant gain would be required to reach this density. Even at the highest rates observed (2 introns per year), this intron density requires 1 billion years of steady intron accretion, still presumably predating the prokaryote–eukaryote splits.

This apparent paradox suggests that recent intron creation may be very different from the process that created the first spliceosomal introns. Two such two-tiered systems have been proposed. First, the introns present in the plant–animal ancestor could have been largely due not to insertion, but to retention of introns present at the time of formation of their resident genes, as envisioned by the introns-early hypothesis. The number of such introns would thus be unrelated to more recent intron insertion rates.

Alternatively, introns in early eukaryotes could also have been gained, but by difference processes than more recent gains. Indeed, proposed models for insertion of new introns (intron transposition, ref. 2; transposon insertion, ref. 69; tandem genomic duplication, ref. 70; and transfer of introns from paralogs through gene conversion, ref. 71) assume a preexistent spliceosome and cannot explain the initial emergence of the spliceosomal system. Yet the only proposed model that offers such an explanation, transfer of type II introns from bacterial endosymbionts (5), cannot explain observed recent intron gains in species whose endosymbionts lack such introns (e.g., ref. 44). Thus, if any proposed models of intron gain are correct, new intron gains in at least some species must result from processes different from those that created the first spliceosomal introns.

The first introns could have arisen by a major event in early eukaryotic evolution coincident with the creation of the splicing machinery, most plausibly a massive invasion of the eukaryotic nucleus by type II introns from early endosymbionts (5). At this time, the self-splicing type II intron apparatus would have transformed into the nascent eukaryotic spliceosome (72). More recent introns could then arise either by further type II intron insertions or completely unrelated processes. In this case, early arising introns would be well defined, truly homologous, type II-related elements; more recent introns would not necessarily be homologous either to earlier-arising introns or to each other. Instead, new introns would arise from any mutation causing an insertion of sequence into a coding region that is then efficiently removed from transcripts by the spliceosome.

An additional corollary of our results, depending on the phylogeny (e.g., ref. 73), concerns the intron density of the common ancestor of apicomplexans with plants, animals, and fungi. Although the lack of an outgroup in the data set prohibits direct estimation of the number of introns present in that ancestor, we can make inferences assuming that intron loss rates in those deepest branches were similar to rates observed in other branches. Assuming the branches from the Plasmodium crown divergence [assumed to be 1.75 billion years ago (Bya)] to the crown ancestor (assumed 1.5 Bya) and to modern Plasmodium experienced a low rate of intron loss similar to rates in chordates and plants (say 3.5 × 10–10 per year) gives an estimate of 305 introns in the deep ancestor in the studied regions. Assuming a high rate of loss such as that found along other branches (say 1.5 × 10–9 per year) yields an estimate of 4,099 introns, more than in any studied species. The presumably unicellular character of such an ancestor suggests evolutionary pressures more similar to those in yeast than in vertebrates, favoring the latter estimate and suggesting extraordinarily deep intron-rich eukaryotic ancestors. Using the average estimated rate of loss over all external branches (1.24 × 10–9) gives an estimate of 1,948 introns in this ancestor, close to the estimates for the crown group and opisthokont ancestors (Fig. 3). Intron-dense gene structures thus may be even older than previously appreciated.

Using similar methods, Nielsen et al. (49) recently found that intron losses and gains in four species of euascomyces fungi had been roughly balanced for the past ≈330 million years. This finding contrasts with the general excess of losses over gains found here and is particularly surprising in view of the observed correlation of intron number with organismal complexity, which might predict high loss rates in euascomyces. One possible explanation is that, having shed most of their unnecessary introns in early fungal evolution, euascomyces have experienced a more recent equilibration in intron number. A large fraction of the few remaining ancestral introns could be retained because of some selective advantage, whereas other introns are gained and lost in roughly equal numbers.

Conclusion

These results illuminate the relative importance of intron loss and gain in eukaryotic evolution. Rates of loss of existent introns are slightly lower than nucleotide substitution rates. The rate at which introns are gained per site is orders of magnitude smaller. Over a range of external branches, the ratio of total intron losses to gains varies from one-half to five. Studied lineages appear to be gaining introns at a rate that cannot explain the apparently high intron density of very early eukaryotic genomes, suggesting that the processes of intron birth in early eukaryotes could be fundamentally different from the processes in more recent evolution.

Abbreviation: MLE, maximum likelihood estimates.

References