Estimating the Selective Effects of Heterozygous Protein Truncating Variants from Human Exome Data (original) (raw)

. Author manuscript; available in PMC: 2017 Oct 3.

Published in final edited form as: Nat Genet. 2017 Apr 3;49(5):806–810. doi: 10.1038/ng.3831

Abstract

The dispensability of individual genes for viability has interested generations of geneticists. For some genes it is essential to maintain two functional chromosomal copies, while others may tolerate the loss of one or both copies. Exome sequence data from 60,706 individuals provide sufficient observations of rare protein truncating variants (PTVs) to make genome-wide estimates of selection against heterozygous loss of gene function. The cumulative frequency of rare deleterious PTVs is primarily determined by the balance between incoming mutations and purifying selection rather than genetic drift. This enables the estimation of the genome-wide distribution of selection coefficients for heterozygous PTVs and corresponding Bayesian estimates for individual genes. The strength of selection can discriminate the severity, age of onset, and mode of inheritance in Mendelian exome sequencing cases. We find that genes under the strongest selection are enriched in embryonic lethal mouse knockouts, putatively cell-essential genes, Mendelian disease genes, and regulators of transcription. Screening by essentiality, we find a large set of genes under strong selection that likely have critical function but have not yet been extensively annotated in published literature.

The evolutionary cost of gene loss is a central question in genetics and has been investigated in model organisms and human cell lines1–3. In humans, the question of dispensability and haploinsufficiency of individual genes is intimately related to their causal role in genetic disease. However, estimates of the selection and dominance coefficients in humans have proved elusive as inference techniques used in other sexual organisms generally require cross-breeding over several generations.

The analysis of patterns of natural genetic variation in humans provides an alternative approach to estimating selection intensity and dispensability of individual genes. Despite substantial methodological progress in the ascertainment and analysis of population sequence data4–8, estimation of parameters of natural selection in humans has been complicated by genetic drift, complexities of human demographic history4,5,7,9–12 and the role of non-additive genetic variation13–15. Additionally, naturally occurring PTVs are infrequent in the population, so datasets of thousands of individuals are underpowered for the estimation of gene dispensability in humans.

The Exome Aggregation Consortium (ExAC) dataset now provides a sufficiently powered sample to assess the selection that constrains the number of gene-specific PTVs in the general population16. We restrict our analysis to PTVs predicted to be consequential17, which allows the assumption that all PTVs within a gene likely incur the same selective disadvantage. We can then treat each gene as a bi-allelic locus with a functional state and a loss-of-function state. In each gene, the cumulative frequency of rare deleterious PTVs (the sum of PTV allele frequencies throughout the gene) is then primarily determined by the balance between incoming mutations and selection rather than reassortment of alleles by stochastic drift. This makes our estimates robust to drift, population structure and historical changes in population size, which we evaluate analytically and with simulations (Methods and Supplementary Figure 1).

Using population frequency data from 60,706 individuals without severe Mendelian disorders, we estimate both the overall distribution of gene-based fitness effects and individual gene fitness cost in heterozygotes. Given gene-specific estimates of the de novo mutation rate18,19, the observed number of PTV alleles throughout each gene, and number of chromosomes sampled, we estimate the genome-wide distribution of selective effects for heterozygous PTVs, _s_het. We parameterize the distribution of selective effects using an inverse Gaussian, which is fit using maximum likelihood (Figure 1). We then estimate individual gene selection coefficients using the posterior probability for _s_het given gene-specific values of the observed number of PTVs, number of chromosomes sampled and estimated mutation rate (Supplementary Table 1).

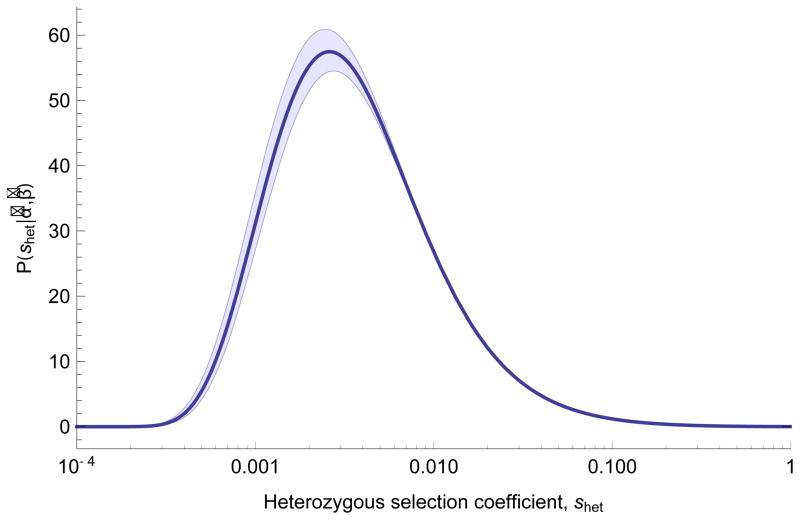
Figure 1.

Figure 1

Inferred distribution of fitness effects for heterozygous loss of gene function. Estimates of parameters (α̂, β̂) from maximum likelihood fit to the observed distribution of PTV counts across 15,998 genes in terciles of mutation rate, assuming _s_het ~ IG(α, β). Shaded areas show 95% CI obtained from 100 bootstrapping replicates, intended to quantify the influence of sampling noise in the data set on parameter inference, with fixed estimates of local mutation rate.

Although the distribution is broad, suggesting the effect of losing one copy of a gene is variable, the mode of the distribution corresponds to a fitness loss around 0.5% (_s_het = 0.005). Despite the large sample size, resolution to distinguish between very high selective effects is limited. There are 2,984 genes with _s_het > 0.1, a result concordant with previous estimates of loss of function intolerance derived from population data16. Even though some genes are heavily depleted of PTVs in ExAC as compared with mutational expectation, these values suggest that heterozygote PTVs in many genes are not necessarily responsible for observable, severe clinical consequences.

Unsurprisingly however, Mendelian diseases genes have higher _s_het values. Among them, genes annotated exclusively as autosomal dominant (AD, N=867) have significantly higher _s_het values than those annotated as autosomal recessive (AR, N=1,482)20 [Mann-Whitney p-value 3.14×10−64] (Figure 2[a,b]). This suggests it may be possible to prioritize candidate disease genes identified in clinical exome sequencing analysis using the observed mode of inheritance and _s_het value.

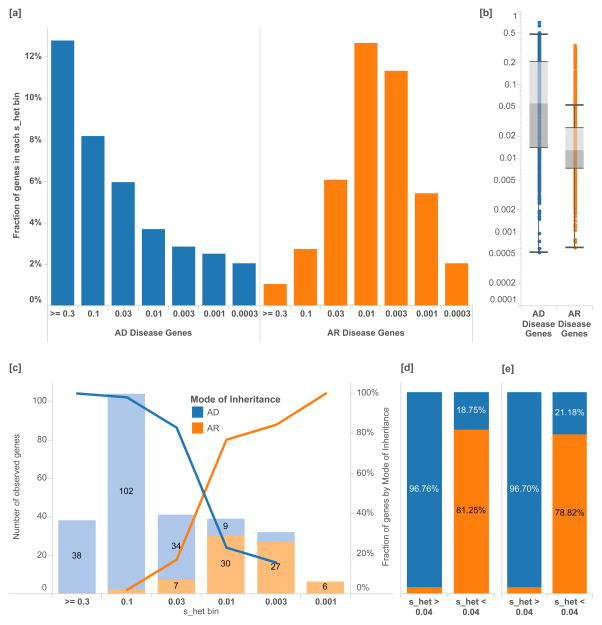
Figure 2.

Figure 2

Separation of disease genes and clinical cases by mode of inheritance. [a] The percentage of genes associated with exclusively autosomal dominant (AD, N=867) disorders versus autosomal recessive (AR, N=1,482) disorders as annotated by the Clinical Genomics Database (CGD) in each _s_het bin. Logarithmic bins are ordered from greatest to smallest _s_het values. [b] Overall, AD genes have significantly higher _s_het values than AR genes [Mann-Whitney U p-value 3.14×10−64]. [c] Similarly, in solved Mendelian clinical exome sequencing cases (Baylor)21, _s_het values can help discriminate between AR and AD disease genes, as annotated by clinical geneticists. [d] A _s_het value of 0.04 can be used as a simple classification threshold for AD genes with a PPV of 96%. [e] This finding is replicated in a separately ascertained sample from UCLA. Box plots range from 25th–75th percentile values and whiskers include 1.5 times the interquartile range.

In 504 clinical exome cases that resulted in Mendelian diagnosis21, we find a similar enrichment of cases by MOI and selection value (Figure 2[c]). We find that 90.4% of novel, dominant variants are associated with heterozygous fitness loss greater than 0.04 (Figure 2[d]). Among disease variants, a cutoff of _s_het > 0.04 provides a 96% positive predictive value for discriminating between AD and AR.

To test the generalizable utility of prioritizing candidate genes in Mendelian sequencing studies using _s_het, we compared the overall prevalence of genes with _s_het > 0.04 to the corresponding fraction in an independently ascertained dataset of new dominant Mendelian diagnoses (Figure 2[e])22. This analysis suggests that restricting to genes with _s_het > 0.04 would provide a three-fold reduction of candidate variants, given the overall distribution of _s_het values. Thus, initial effort in clinical cases can be focused on just a few genes for functional validation, familial segregation studies, and patient matching. We summarize the classification accuracy (AUC 0.9312) and generate mode of inheritance probabilities for each gene using the full set of clinical sequencing cases (Supplementary Figure 2 and Supplementary Table 2).

Beyond mode of inheritance, we find that _s_het helps predict phenotypic severity, age of onset, penetrance, and the fraction of de novo variants in a set of high-confidence haploinsufficient disease genes (Figure 3). In broader sets of known disease genes, _s_het estimates significantly correlate with the number of references in OMIM MorbidMap and the number of HGMD disease “DM” variants (Supplementary Figure 3).

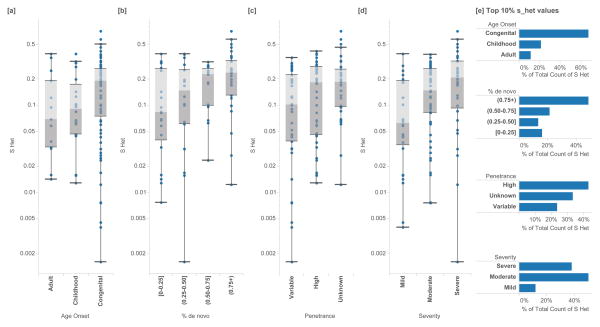
Figure 3.

Figure 3

Enrichments of _s_het in known haploinsufficient disease genes of high confidence (ClinGen Dosage Sensitivity Project). In (N=127) autosomal genes, we annotate the _s_het scores of genes associated with each disease category and classification. Higher _s_het values are associated with [a] earlier age of onset (Mann-Whitney U p=1.46 ×10−2), [b] a larger fraction of de novo variants (p=8×10−5), [c] high or unspecified penetrance (p=1.79 ×10−2) and [d] increased phenotypic severity (p=4.87×10−3). Box plots range from 25th–75th percentile values and whiskers include 1.5 times the interquartile range. [e] Genes with the 10% highest _s_het values are also similarly enriched with more severe clinical annotations.

Gene-specific fitness loss values allow us to plot the distribution of selective effects for different disorders. This provides information about the breadth and severity of selection associated with various disorder groups using both well-established genes (Figure 4[a]) and findings from Mendelian exome cases (Figure 4[b]). Overall, genes involved in neurologic phenotypes and congenital heart disease appear to be under more intense selection compared with other disorder groups, or tolerated knockouts from a consanguineous cohort (Figure 4[c,d])23. Interestingly, genes recessive for these disorders appear to have only partially recessive effects on fitness, so selection on heterozygotes is not negligible in these genes (Figure 4).

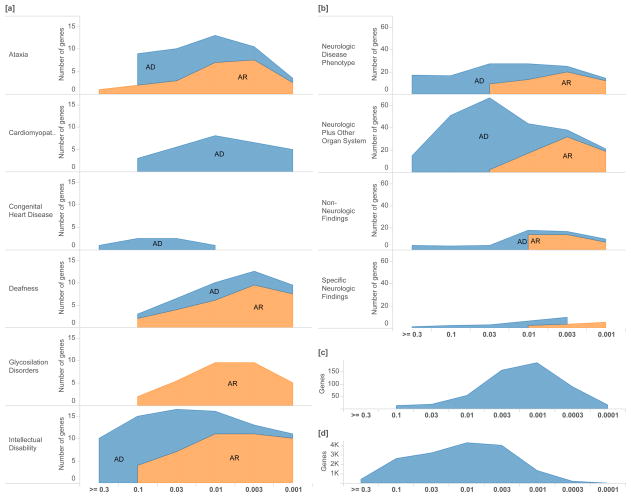
Figure 4.

Figure 4

Distribution of _s_het values for phenotypes in known disease genes and clinical cases. We plot the distribution of selective effects for different disorder groups, providing information about the breadth and severity of selection associated with each group. [a] We include known Mendelian disease genes (Clinical Genomic Database) annotated as either Autosomal Recessive or Autosomal Dominant and [b] clinical exome sequencing cases21. We contrast these with [c] all tolerated knockouts in a consanguineous cohort (PROMIS)23 and [d] the distribution of selective effects in all scored genes. Logarithmic bins are ordered from greatest to smallest _s_het values.

In germline cancer predisposition, genes under stronger selection are enriched in individuals with cancer over those in ExAC (Supplementary Figure 4). This suggests that genes with low _s_het values should not be prioritized in prospective genetic screening for cancer predisposition. Consistent with previous studies18, we find de novo mutations in patients with autism spectrum disorder are significantly enriched in genes under stronger selection than those identified in controls (Supplementary Figure 5 and Supplementary Table 3).

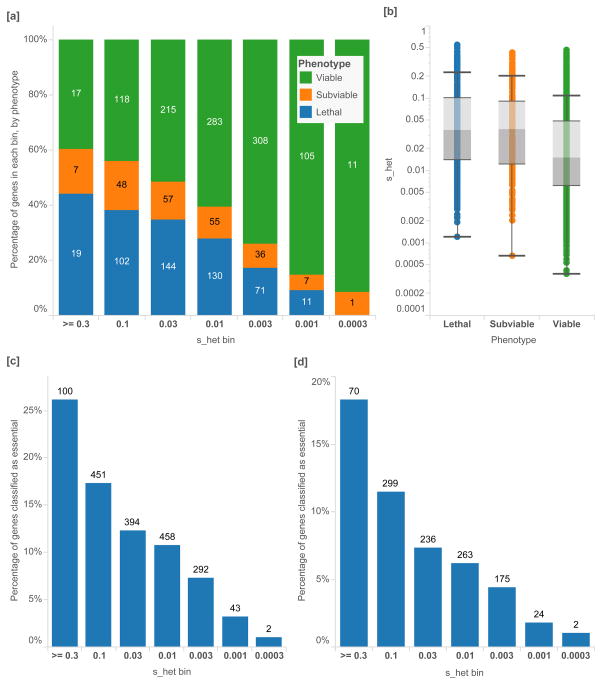
Next, we analyze _s_het in the context of developmental and functional assays. In a large set of neutrally-ascertained mouse knockouts (N=2,179)24, mice that are null mutant for orthologous genes with higher _s_het estimates are enriched for embryonic lethality or sub-viability, while those with the lowest _s_het estimates are depleted for embryonic lethality [Mann-Whitney p=2.95×10−28] (Figure 5[a,b]).

Figure 5.

Figure 5

High-throughput screens of gene essentiality in mice and cell assays, as a percentage of all genes in each _s_het bin. [a] Proportion of orthologous mouse knockout genes by phenotype, from a neutrally-ascertained set of genes generated by the International Mouse Phenotyping Consortium (IMCP). Logarithmic bins are ordered from greatest to smallest _s_het values. [b] ICMP mice are separated into viable (N=1,057), sub-viable (N=211) and lethal knockouts (N=477), and lethal knockouts have significantly higher _s_het values than viable [Mann-Whitney U p-value 2.95×10−28]. [c] Cell-essential genes as reported by Wang et al. 3 from genome-wide KBM-7 tumor cell CRISPR assay (N=1,740) have significantly higher _s_het values [p-value 5.13×10−16] [d] as do genes that were characterized as essential in a gene trap assay (N= 1,081) [p-value = 4.90×10−18]. In the CRISPR assay, all genes with adjusted p-values < 0.05 and negative assay scores are included, and genes with gene trap scores < 0.4 or lower are included. Box plots range from 25th–75th percentile values and whiskers include 1.5 times the interquartile range.

It is well known that mutations that are haploinsufficient in humans can often be well-tolerated when heterozygous in mice25. A classic example is SHH; heterozygous null mutations in this important developmental signaling gene result in holoprosencephaly26. Haploinsufficiency for other genes in this signaling pathway also results in developmental defects; e.g. GLI3 (Pallister-Hall syndrome and Greig cephalopolysyndactyly syndrome)27–29 and GLI2 (Holoprosencephaly 9)30. Interestingly, haploinsufficiency for these genes is tolerated in mouse models; mice heterozygous for null variation in the SHH signaling pathway are phenotypically normal, while homozygous mutant mice have defects that recapitulate features of the human syndrome31–33. This extends to many other human developmental disorders, enabling the experimental characterization of the molecular consequences of these mutations. Thus, it is notable that homozygous null mice in orthologous genes with higher _s_het values are enriched for lethality.

High-throughput genetic analysis of cell-essentiality provides an orthogonal dataset for comparison with _s_het. In genes putatively essential for human cell proliferation using CRISPR-based inactivation (Figure 5[c]) and gene trap inactivation assays3 (Figure 5[d]), we find that essential genes are heavily enriched with high _s_het values [p-values 5.13×10−16, 4.90×10−18, respectively].

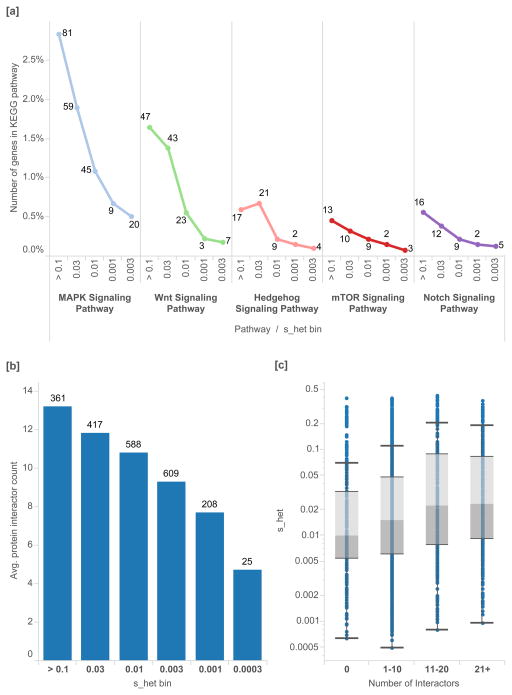
Key developmental pathways are dramatically enriched in genes under strong selection (Figure 6[a]). We also find a significant positive correlation between the number of protein-protein interactions for each gene and its _s_het value (Figure 6[b,c]), identified from high-throughput mass spectrometry data. In the context of molecular and cellular function, a set of genes with very high selective effects (_s_het > 0.15, 2,072 genes) is enriched in biological process categories “transcription regulation” (Bonferroni p=1.8×10−39), “transcription” (7.5×10−36), and “negative regulators of biosynthetic processes” (Supplementary Material)34. Nucleus was the most enriched cellular compartment for these genes (4.8×10−76). The enrichment of transcription factors in these genes is consistent with literature that describes dosage dependence for enzymatic proteins and haploinsufficiency for transcriptional regulators35.

Figure 6.

Figure 6

Protein pathways and protein-protein interactions, as a percentage of the associated developmental genes in each _s_het bin. [a] In key developmental pathways in KEGG, we find that genes with higher _s_het values are enriched in genes important to development. [b] We plot the distribution of the number of protein-protein interactions for each gene, as determined by a genome-wide mass spectrometry assay51 versus _s_het value. [c] We find that _s_het values are positively correlated with the number of observed interactors for each gene. Box plots range from 25th–75th percentile values and whiskers include 1.5 times the interquartile range.

Selection estimates from human PTVs provide a measure of gene dispensability unbiased with respect to existing knowledge. Thus, these estimates may potentially highlight genes playing a key role in development or in maintaining core cellular functions. There are many genes with high fitness costs not previously described in human genetics studies. Given the marked enrichment of genes with high _s_het values associated with Mendelian disorders, cell essentiality, embryonic lethality and development, it is plausible that many genes with high _s_het values that have not been previously associated with human disease may be so detrimental that they are required for embryonic development.

We inspect genes that lack disease annotations and publications but that have high _s_het values to determine whether they share functional and genetic features reminiscent of known genes with central roles in cell housekeeping and developmental biology. We measure the relative knowledge about each gene in the primary literature from Entrez and PubMed36 using the number of gene reports connected with each manuscript, and sum the weighted contributions across all available manuscripts37 (PubMed score, Methods). While the PubMed score is positively correlated with _s_het values, a substantial number of understudied genes fall in the highest _s_het decile (Supplementary Figure 6).

We selected the 250 most cited and least cited genes within the top _s_het decile, and compared their frequency of protein-protein interactions, viability of orthologous mouse knockouts and cell essentiality assays. Genes with the fewest publications (no more than one individual citation) have nearly the same number of embryonic lethal mouse knockouts as genes with the most publications. Other assays are only slightly depleted in genes with the fewest publications (Supplementary Figure 7). These findings suggest there may be additional essential developmental pathways yet to be uncovered in genes under strong selection that lack functional or disease annotations, and provides a promising gene set for further exploration. We have created a prioritized list of genes using developed from functional evidence to indicate the most promising candidates for future functional screening (Supplementary Table 4).

To place our inferences in the broader evolutionary context, we use comparable estimates from model organisms including flies and yeast, based on knockout competition with wild type or explicit crosses. In yeast, the analysis of a library of PTV knockouts provides a mean estimate of _s_het ≈ 0.013, which is close to our inferred results (_s_het ≈ 0.059) in humans38, given that the functional experiments excluded genes with very high s, and we have excluded genes with high cumulative allele frequency. Estimates in flies derived from homozygote lethal mutations which reduce viability in heterozygotes (rather than only PTVs) suggest values of _s_het on the order of 1–3%, which is also in broad agreement with our estimates in humans1,39. While values of s in this range have a small impact in each generation, they may have dramatic evolutionary consequences40.

In conclusion, we use the genome-wide distribution of PTVs to estimate fitness loss due to heterozygous loss of each gene. Unlike recent work on genic intolerance18,41, we explicitly estimate the distribution of selection coefficients for PTVs. Our estimates are also distinct from earlier work on the estimation of fitness effects of allelic variants in humans42 as the large sample size coupled with the assumption of strong selection makes our approach robust with respect to complexities of demographic history and dominance, and allows gene-based inferences. Conversely, our assumptions are justified for many but not all genes, as the method has limited resolution for genes under the strongest and weakest selection. These results may be useful in Mendelian disease gene discovery efforts and provide clinical utility in the inference of severity and mode of inheritance underlying Mendelian disease.

Data Availability

The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files. All original population frequency data are available through the ExAC Aggregation Consortium [http://exac.broadinstitute.org/]. Updated selection estimates will be made available at: [http://genetics.bwh.harvard.edu/genescores/].

Online Methods

Model of deterministic mutation-selection balance

For most genes, protein-truncating alleles are both individually and collectively rare. For genes where they are collectively rare, estimation of the selective effect against heterozygous PTVs (s_het ) can be greatly simplified. We model each gene as a single bi-allelic locus with cumulative frequency X_= Σ_jxj, where the sum is over PTVs in gene i for PTV sites j. This is motivated by the simplifying assumption of identical selection coefficients for all PTVs within a gene, and the observation that the frequency of the vast majority of PTVs is extremely low such that the occurrence of multiple variable sites within a gene on a single haplotype is also extremely low (2_Nxijxik < 1 for sample size N). Moreover, multiple PTVs in a gene in an individual would be functionally equivalent to a single PTV resulting in a loss of function state.

Then for each gene, the cumulative allele frequency X is influenced by incoming mutation, selection and the random reassortment of alleles (genetic drift). When selection is strong, s ≫ 2.5×10−5 (i.e. when 4_Nes_ ≫ 1, with effective population size Ne 104), drift is much smaller than the contribution of selection. Furthermore, the strength of genetic drift is weakest for genes at low frequencies: for a variant with cumulative frequency of X = 0.001 the expected frequency change due to drift is only 〈Δ_X_2〉~X/4_Ne_ = 2.5×10−8 per generation. Notably, at the locus level assuming X ≪ 1 the drift contribution is also much smaller than the mutational influx. Hence under strong selection and for small allele frequencies the expected cumulative frequency of PTVs is determined by the equilibrium between the influx of de novo mutations (estimated to increase the cumulative frequency by an average 1.4×10−6 per locus per generation by mutational model) and the outflux due to natural selection.

In the presence of selection on both heterozygotes and homozygotes and ignoring back mutations, the dynamics of X are captured by the following equation:

∂tX=-shetX(1-X)-shomX2(1-X)+U (1)

Here U represents the PTV mutation rate at the gene locus per individual per generation, and _s_het = > 0 and s_hom = > represent the strength of negative selection against PTV heterozygotes and homozygotes, respectively. We note that compound heterozygotes (with a single PTV on each chromosome) are treated as homozygotes under the bi-allelic assumption. Provided X ≪ 1, as is the case for PTVs under strong selection (2_Nes ≫ 1 ), this equation simplifies dramatically:

Because X ≪ 1, selection against heterozygotes (the linear term) generally also dominates over selection against homozygotes (the quadratic term), provided _s_het/_s_hom ≫ X. This is only violated in cases of extreme recessivity (where the dominance coefficient h ≪ 0.001 ), but even in that case the expected cumulative frequency of PTVs in essential genes is unlikely to exceed 0.001 (the characteristic X in the completely recessive case is U/s~10-3 when _s_~1, see simulations in Supplementary Figure 1). The strong selection regime thus corresponds to mutation-selection balance in the heterozygote state of a PTV mutation. In our model, we do not assume that selection acts exclusively on heterozygotes, but aim at estimating only fitness loss due to the lack of one functional copy of a gene. Even in the case of strong selection against homozygotes, the population frequency is primarily controlled by efficient selection against heterozygotes.

Notably, there is no dependence on the demography or population size in this regime, as the contribution from drift vanishes because selection drives alleles out of the population efficiently and on very short time scales. Classic papers by Li43,44 and Maruyama45,46 showed that relevant time scales are short, even in the case of exponential expansion, because individual deleterious alleles are predominantly recent, with an allelic age on the order of 1/s. Current estimates of recent population histories for most of populations included in the ExAC dataset suggest that 4_Ns_ safely exceeds 1. Even if individual alleles are subject to stochastic drift, this effect is mitigated by the aggregation of variants on the gene level. One possible concern is the inclusion of individuals with Finnish ancestry, as this population underwent an intense, relatively recent bottleneck. We address this population explicitly using forward simulations and by removing them from our analysis to show no significant deviation from our initial estimates in their absence (below).

From Eq. 2 follows that for a population sample of size N chromosomes, sample allele counts n = NX̂ = N_Σ_j x̂j are expected to be Poisson distributed around the expectation given by:

Generally, genes under the strongest and weakest selection are expected to have greater estimation uncertainty, as the resolution to estimate _s_het deteriorates when variants are so common that they may not only be controlled by heterozygote selection, but also by drift or complex demography. However, the overwhelming majority of genes conform to our assumptions of cumulative PTV allele frequency not exceeding 0.001. Despite issues such as the admixture of populations, consanguineous samples in ExAC23, and the Wahlund effect, very few genes (1,201 of 17,199 covered genes) have higher estimated cumulative allele frequencies X̂, which we restrict from the estimation procedure. On the other end of the spectrum, genes under strong selection may lack PTVs by chance alone in ExAC, which limits the ability to distinguish between large selective effects.

Population genetics simulations of model assumptions

To validate the assumption that estimates of selection can be made under mutation-selection balance independent of demography or population size for variants under sufficiently strong selection, we used SLiM 2.0 to conduct forward population genetics simulations47. We ran 10,000 replicates each of simulations with selection coefficients of −5×10−1, −5×10−2, −5×10−3, −5×10−4, and −5×10−5 through a realistic demography derived from previously published histories for African, Non-Finnish European, and Finnish populations48,49 (Supplementary Figure 1). We compare the theoretical expectation of cumulative allele frequency (U/_s_het [Equation 3]) with the simulated cumulative allele frequency. We do this in three populations (African, Non-Finnish European and Finnish), plus a “Combined” population which includes pooled site frequency spectra from all three populations in proportions represented in the ExAC dataset. The simulations support our assumption of mutation-selection balance in the strong selection regime (|_s_het| >= 1×10−3), which appears to be appropriate for PTVs. This is true for all three populations examined and for the combined population, demonstrating that this assumption is robust to differences in the strength of drift due the distinct demographic histories of included human populations.

All simulations had a length of 1 kilobase, mutation rate of 2×10−8 per generation per base pair, and recombination rate of 1×10−5 per generation per base pair. The high recombination rate was chosen to simulate largely unlinked sites, as we are simulating PTVs which are infrequent enough that they are expected not to be in linkage with other PTVs in the same gene.

Dataset for _s_het estimation

In this analysis, we use Exome Aggregation Consortium (ExAC) dataset version 0.3, a set of jointly-called exomes from 60,706 individuals ascertained with no known severe, early-onset Mendelian disorders. The mean coverage depth was calculated for each gene (canonical transcript from Ensembl v75, GENCODE v19) in the ExAC dataset (mean 57.75; s.d. 20.96). Genes with average coverage depth of at least 30x were used in further analysis (N=17,199). Single nucleotide substitution variants annotated as PASS quality with predicted functional effects in the canonical transcript of “stop_gained”, “splice_donor”, or “splice_acceptor” (as annotated by Variant Effect Predictor) were included in the analysis. Variants such as indels, in-frame mutations, and frameshift variants were excluded from this analysis, as many of these variants may have annotation issues or may not be functionally impactful. Along the same lines, we are mindful that not all PTVs will result in complete loss of gene function, due to alternative transcripts or nonsense mediated decay. To address this, variants were filtered using LOFTEE50 and restricted to those predicted with high confidence to have consequences in the canonical transcript.

For each of the 17,199 genes we have observable values for (n, U, N), where n denotes the total number of observed PTV alleles in the population sample of N chromosomes covered in the gene, and U the PTV mutation rate across the canonical gene transcript from a mutational model18,19. Values of U for each gene from Samocha et al. were used along with the number of well-covered chromosomes N in each gene to generate the null mutational expectation of neutral evolution, NU. Incorrectly specified values from this mutational model could alter estimates of selection for individual genes, as higher estimates of selection are made in genes with greater depletions from the null expectation model. Our inference of selection coefficients relies on the assumption that the cumulative population frequency of PTV mutations, X, is small due to strong negative selection, so genes with X̂ = n/N > 0.001 are omitted from the analysis, leaving 15,998 genes.

Estimation of P(_s_het)

A genome-wide ensemble of observed (n) and expected (NU ≡ ν ) genic PTV counts enables the inference of the distribution of heterozygous loss-of-function fitness effects, P(_s_het), which underlies the evolutionary dynamics of this class of mutations. We estimate the parameters (α,β) of this distribution by fitting the observed distribution of PTV counts across genes:

P(n∣α,β;ν)=∫P(n∣shet;ν)P(shet;α,β)dshet. (4)

For a given gene under negative selection PTV mutations are rare events, such that we expect a Poisson distribution for the likelihood of the observed number of PTVs P(n|_s_het; ν) = Poiss(n;λ), where λ = ν/_s_het (Eq. 3). We parameterize by using the functional form of an inverse Gaussian distribution, i.e. P(_s_het; α,β) = IG(_s_het; α,β), so Eq. 4 becomes:

P(n∣α,β;ν)=∫Poiss(n;λ=ν/shet)IG(shet;α,β)dshet=1n!eβα2βπα(να)n(ββ+2ν)1+2n4K12+n(β(β+2ν)α), (5)

where Kn(z) is the modified Bessel function of the second kind. To estimate parameters of the distribution of selection coefficients, P(_s_het;α,β), we fit Eq. 5 to the observed distribution of PTV counts, Q(n) by maximizing the log-likelihood

log[L(α,β∣{n})]=log∑i=1GP(ni∣α,β;νi) (6)

on the regime α ∈ [10−2, 2] and β ∈ [10−4, 2], where G is the number of genes. In order to account for a slight positive correlation between the mutation rate and selection strength (Supplementary Figure 8), we separately perform the fit on U terciles of the data set and combine the results in a mixture distribution with equal weights. The mean mutation rates in the three terciles are _Ū_1 = 4.6 · 10−7, _Ū_2 = 1.1 · 10−6, and _Ū_2 = 2.6 · 10−6. We estimate (_α̂_1, _β̂_1) = (0.057±0.010,0.0052±0.0003), (_α̂_2, _β̂_2) = (0.046±0.005,0.0087±0.0004), and (_α̂_2, _β̂_2) = (0.074±0.005,0.0160±0.0005), with error margins denoting two s.d. from 100 bootstrapping replicates of the set of ~5,333 genes in each tercile. This error estimate is intended to quantify the effect of the sampling noise in the data set on the parameter inference while local mutation rate estimates are assumed fixed. The resulting fitted distributions of counts are shown in Supplementary Figure 9 together with the corresponding Q(n), while Figure 1 shows the inferred P(_s_het; α̂, β̂) = (IG(_s_het; _α̂_1, _β̂_1) + (IG(_s_het; _α̂_2, _β̂_2) + (IG(_s_het; _α̂_3, _β̂_3))/3. The choice for the functional form of P(_s_het) is motivated by the shape of the empirical distribution of the naïve estimator ν/n (given by a simple inversion of Eq. 3). We also compared the log-likelihood of the fit to Q(n) obtained with this model to that obtained from two other two-parameter distributions, _s_het ~ Gamma and _s_het ~ InvGamma, and chose the model with the highest likelihood, which is _s_het ~ IG.

To assess the relative change in the distribution of heterozygote selection coefficients when different population subsets are included, we first estimated the distribution of _s_het using only non-Finnish Europeans (NFE) in Supplementary Figure 10. We find high concordance between the overall distribution generated using all ExAC samples and NFE specific estimates. We also separately removed Finnish individuals from the estimation of the distribution of selection coefficients, and find very high concordance between estimates made using all ExAC samples and ExAC without Finnish individuals (Supplementary Figure 11). These analyses demonstrate that the model is robust to concerns about recent demographic history in Finnish individuals, supporting the validity of the deterministic approximation. We cannot completely rule out the possibility that other included populations may have issues related to complexities of their recent demographic history.

Inference of _s_het on individual genes

From the inferred distributions P(_s_het; α̂t, β̂t) in each tercile t of the mutation rate U, we construct a per-gene estimator of _s_het for genes in the tercile using the posterior probability given n, which mitigates the stochasticity of the observed PTV count:

P(shet,i∣ni;νi)=P(ni∣shet,i;νi)P(shet,i;α^t,β^t)∫P(ni∣s;νi)P(s;α^t,β^t)ds, (7)

where the denominator is given by Eq. 5. Supplementary Table 1 provides the mean values derived from these posterior probabilities for each gene.

Predicted mode of inheritance in clinical exome cases

We trained a Naïve Bayes classifier to predict the mode of inheritance in a set of solved clinical exome sequencing cases from Baylor College of Medicine (N=283 cases)21 and UCLA22 (N=176 cases). Using data from UCLA as the training dataset, we are able to cross-predict the mode of inheritance in separately ascertained Baylor cases with classification accuracy of 88.0%, sensitivity of 86.1%, specificity of 90.2%, and an AUC of 0.931. Genes that were related to diagnosis in both clinics (overlapping genes) were removed from the larger Baylor set (Supplementary Figure 2).

Using a logistic regression based on the full set of cases from Baylor and UCLA, we generated predictions for all 15,998 genes where there is a _s_het value (Supplementary Table 4).

Mouse knockout comparative analysis

We reviewed mouse knockout enrichments from two datasets: the full set of mouse knockouts from a neutrally-ascertained mouse knockout screen (N=2,179 genes) generated by the International Mouse Phenotyping Consortium24. Genes were classified as ‘Viable’, ‘Sub-Viable’, or ‘Lethal’ based on the results for the assay.

PubMed gene score and enrichment analysis

We developed a score to estimate the relative importance of each gene in the published medical and scientific literature. First, we connected literature from Entrez which included both PubMed citations and references to Entrez genes. We assigned a weight to each article referencing a gene of 1/ai, where ai was the number of genes referred to by article i. For example, an article referring to four genes would receive a weight of 1/4. Finally, we assigned each gene a score which was the sum of the weighted article scores. These scores ranged from 4,672 articles per gene (p53) to 0.0001 articles/gene.

Next, we focused on genes that are estimated to be under very strong selection but that lack functional or clinical annotations. In the top decile of _s_het values, we separated the top 250 and bottom 250 genes by PubMed score. We then annotated each of these with unbiased genome-wide assays, including the number of protein-protein interactions (as determined by a genome-wide mass spectrometry assay)51, whether each gene is determined to be cell-essential in genome-wide CRISPR and gene trap assays3, and whether there is a mouse knockout in the neutrally-ascertained orthologous nonviable mouse knockout52. To limit the number of genes with incorrect _s_het estimates in this set of 500 genes, we pre-filtered any genes with only a single exon, as they may be enriched for recent pseudogenes, and also removed any olfactory, mucin, and zinc finger proteins.

Functional enrichment analysis

We inspected the functional annotations related to approximately the top 10% of selectively disadvantageous genes (with _s_het > 0.15, N=2,072 genes) that were successfully mapped using Database for Annotation, Visualization, and Integrated Discovery (DAVID) version 6.734, DAVID. Separately, two other cutoffs (_s_het > 0.25, N=897 genes and _s_het > 0.5, N=32 genes) were also tested and similar results were identified.

Using DAVID, we identified functional annotation terms and keywords that were enriched and clustered. Functional annotation terms were generated using the Functional Annotation tool, which includes protein information resource keywords, GeneOntology (GO) terms, biological processes and pathways, and protein domains. Using the default settings (Count 2 and EASE 0.1), 247 statistically significant (Bonferroni corrected) terms were identified and are included in Supplementary Table 5.

Using the DAVID Functional Annotation clustering feature, we identified clusters using the same set of 2,072 genes with the default settings. The first annotation cluster includes core, essential cellular components including the nuclear lumen, nucleoplasm, organelle lumen (Enrichment score 32.63), and the second includes transcription regulation and transcription factor activity (Enrichment score 27.94), detailed in Supplementary Table 6.

Supplementary Material

1

2

3

4

5

6

7

Acknowledgments

This work was supported by National Institutes of Health Grant HG007229 (C.C.), GM078598 (S.S., D.J., D.J.B.), and MH101244 (S.S., D.W.). We thank I. Adzhubei, K. Karczewski, and A. Kondrashov for helpful advice.

Footnotes

Author Contributions

Overall concept and approach conceived and developed by C.C., D.B., and S.S. Implementation, data analysis and interpretation conducted by C.C., D.W., D.J.B., D.J., and D.N. Datasets and helpful advice were provided by D.M., M.D., K.S., and A.O. The article was written by C.C. and S.S. with contributions from D.W. and D.J.B. All authors read and discussed the manuscript.

Competing Financial Interests Statement

The authors have no competing interests as defined by Springer Nature, or other interests that might be perceived to influence the results and/or discussion reported in this paper.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1

2

3

4

5

6

7

Data Availability Statement

The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files. All original population frequency data are available through the ExAC Aggregation Consortium [http://exac.broadinstitute.org/]. Updated selection estimates will be made available at: [http://genetics.bwh.harvard.edu/genescores/].