Developing and evaluating polygenic risk prediction models for stratified disease prevention (original) (raw)

. Author manuscript; available in PMC: 2018 Jun 27.

Published in final edited form as: Nat Rev Genet. 2016 May 3;17(7):392–406. doi: 10.1038/nrg.2016.27

Abstract

Knowledge of genetics and its implications for human health is rapidly evolving in accordance with recent events, such as discoveries of large numbers of disease susceptibility loci from genome-wide association studies, the US Supreme Court ruling of the non-patentability of human genes, and the development of a regulatory framework for commercial genetic tests. In anticipation of the increasing relevance of genetic testing for the assessment of disease risks, this Review provides a summary of the methodologies used for building, evaluating and applying risk prediction models that include information from genetic testing and environmental risk factors. Potential applications of models for primary and secondary disease prevention are illustrated through several case studies, and future challenges and opportunities are discussed.

Common chronic diseases have complex, multifactorial aetiologies that involve the interplay of both genetic susceptibility and environmental risk factors, which are broadly defined as lifestyle, behavioural, occupational or environmental exposures, and other health conditions. Historically, family-based linkage studies have led to the identification of rare high-penetrant mutations underlying some of these diseases, such as those in the breast cancer 1 (BRCA1) and BRCA2 genes for breast and ovarian cancers, and in multiple genes involved in Lynch syndrome, which predisposes individuals to colorectal and other cancers. With these discoveries, genetic testing became part of the clinical management of individuals in high-risk families in whom there is a high disease burden caused by the variants. The cost of genetic testing has declined following technological advances and the recent ruling by the US Supreme Court stating that genes cannot be patented; consequently, debate has now shifted towards the implications of performing genetic testing in the general population (for example, BRCA1 and BRCA2 mutation testing)1,2. Debate has also begun on standards for the regulation and clinical utility of increasingly available commercial gene-panel tests, which may screen for high-to moderate-penetrance susceptibility variants for various diseases3–6.

As the majority of cases of common diseases do not occur in highly affected families, the development of broad public health strategies for disease prevention requires the identification of risk factors that contribute to the substantial burden of disease in the general population. Recent genome-wide association studies (GWAS) have clearly shown that common single-nucleotide polymorphisms (SNPs) have important roles in defining susceptibility to common diseases. For any given disease, there could be a large number of underlying susceptibility SNPs, each exhibiting only modest disease association, but in combination they could explain a significant portion of the variation in disease incidence in the general population. The success of GWAS indicates that gene-panel and whole-genome tests will continue to emerge in the future for the assessment of polygenic disease risks. This will require critical evaluation of both the statistical validity of the estimated risk and its potential clinical or public health utility.

The utility of genetic testing for disease prevention cannot be fully evaluated unless it is assessed along with environmental factors, which may not only be important determinants of risk but could also be potentially modifiable through changes in lifestyle or appropriate interventions. Thus, there is a need for continuous development and evaluation of risk models that incorporate our expanding knowledge of the risk factors for diseases. Critical to this research are epidemiological prospective cohort studies that can take advantage of the increasingly available electronic medical records, technological advances in the collection and analyses of biological specimens, and big data management platforms and analytics. Steps are being taken towards attaining these goals, as demonstrated by the establishment of new cohorts and biobanks, including UK Biobank, China Kadoorie Biobank, the German National Cohort7, the American Cancer Society’s Cancer Prevention Study-3 and the US National Institutes of Health’s Precision Medicine Initiative Cohort Program announced by President Obama in 2015.

In this Review, we provide an overview of the different steps for building and evaluating models to estimate the disease risks of individuals in the general population based on polygenic risk associated with common SNPs and environmental risk factors (FIG 1). We emphasize the importance of building absolute risk models for clinical applications. We review the criteria for evaluating the statistical validity and clinical utility of models. Using several recent examples from the literature, we illustrate potential applications of absolute risk models for primary and secondary disease prevention. Future challenges and opportunities in risk modelling and in its translation to the clinic are also briefly discussed.

Figure 1. Steps for building and evaluating absolute risk models for the general population.

Figure 1

The flowchart shows the different steps involved in building and evaluating models for the estimation of disease risks of individuals in the general population based on polygenic risk associated with common single-nucleotide polymorphisms (SNPs) and environmental risk factors. Adapted with permission from David Check, US National Institutes of Health.

Risk stratification overview

In broad terms, the clinical utility of a risk model largely depends on its ability to stratify a population into categories with sufficiently distinct risks to substantially affect the risk–benefit balance of public health or clinical interventions (FIG. 2). As illustrated below through several case studies, the evaluation of absolute risks — that is, the probability that an asymptomatic individual will develop the disease over a certain time interval — is critical for determining the risk–benefit implications for each individual. The absolute risk thresholds to determine how individuals should be assigned to distinct risk categories will depend on the risk–benefit implications of specific procedures in the underlying population. The uptake of recommendations for health interventions may also vary from individual to individual based on their personal preferences and values.

Figure 2. Hypothetical distribution of absolute risk for breast cancer.

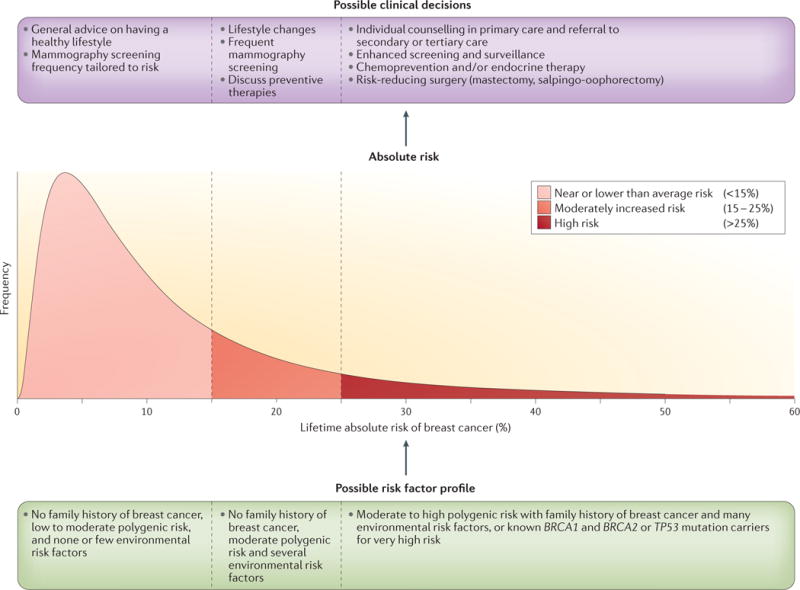
Figure 2

Risk stratification of the population based on a hypothetical distribution of the lifetime risk of breast cancer — that is, the probability that a woman in the population is diagnosed with breast cancer between the ages of 30 and 80 years. A comprehensive model including genetic and environmental risk factors can be used to obtain estimates of the absolute risk of individuals in the population. Women may make different lifestyle choices or decisions about possible preventive interventions depending on their level of risk and their personal values. The more spread the model-based distribution of risk in the population is, the larger the number of individuals the model will be able to assign to risk categories for which the risk–benefit implications of potential interventions could be different. BRCA1, breast cancer 1; TP53, tumour suppressor p53. Adapted with permission from David Check, US National Institutes of Health.

The risk stratification ability of a model depends on how much variation in estimated risk it can provide in an underlying population. In the absence of any known risk factor, the risk of all individuals may be estimated by the average risk for the whole population, potentially using data from population-based registries. Such a model for estimating risk, however, will not provide any variation in risk estimates across individuals and thus would not be useful for risk stratification. As more risk factors are identified for a disease and incorporated into a model, assigned risks will be more variable between individuals and a larger proportion of people could be identified as belonging to more extreme risk categories.

Heritability and polygenic risk scores

Estimates of heritability from different sources can be used to understand the limits of genetic risk stratification8,9. Notwithstanding the differences in various definitions of heritability based on the choice of scale used10, all measures of heritability essentially relate to the degree of variation in the ‘true’ polygenic risk score (PRS) for individuals in the underlying population. In this Review, the PRS of an individual is defined as a quantitative measure of the total genetic risk burden of the disease over multiple susceptibility variants. Risk associated with the true PRS, which is unobserved, is defined by a weighted combination of common, intermediate and rare variants that cause disease susceptibility, and by the interactions within and between these different types of variants. The ability of different types of variants and associated effects to contribute to risk stratification depends on their relative contribution to total heritability.

Historically, family studies have long been used to assess the heritability of diseases, as underlying genetic components of variability are expected to determine, to a large extent, the correlation among disease statuses in related individuals. Recent developments in mixed-model techniques11–14 have facilitated the estimation of various components of heritability using genome-wide sets of markers. Intuitively, these methods use the marker sets to define a genetic distance, sometimes referred to as a kernel function, between pairs of individuals in the study sample. The regression relationship between the genetic and phenotypic similarity of pairs, after adjustment for ascertainment and relatedness of the subjects, can be used to estimate specific components of heritability depending on the set of genetic markers and the type of effects incorporated in the underlying kernel function. For example, pioneering techniques such as genome-wide complex trait analysis (GCTA) and various extensions have been recently used to analyse population-based GWAS and have shown that the additive effects of common variants explain a very substantial fraction of heritability across almost all common complex diseases15–21. Furthermore, analyses of GWAS markers for related subjects and ethnically admixed samples have been used to obtain estimates of heritability, which include contributions of rare variants that are not tagged by GWAS markers in the general population22,23.

However, the use of estimates of heritability as a guide for the future potential of genetic risk-prediction models has several caveats. Estimates based on studies of familial aggregation could be biased owing to confounding by shared environmental factors. Nevertheless, modelling of familial aggregation using different types of relatives with varying degrees of genetic separation (including monozygotic twins and dizygotic twins) has suggested limited contribution of shared environmental factors in familial aggregation of most diseases22,24,25. Estimates of familial risks that are widely reported in epidemiological cohort and case–control studies could be underestimated owing to the poor accuracy of self-reported family history of disease. Case–control studies are also susceptible to biases away from the null owing to differential recall or knowledge of family history of disease reported by cases and controls26–28. Estimates of heritability using mixed-model techniques could also be biased owing to violation of modelling assumptions, mis-specification of disease rate and improper accounting for ascertainment in case–control studies29,30.

Estimates of heritability alone, even when they are unbiased, may not be a useful guide to assess the potential utility of risk stratification. For example, first-degree familial relative risks for a variety of cancers are quite similar and vary between 1.5 and 2.0 (REFS 31–34). Such measures of relative risk quantify the risk in individuals with a family history of disease relative to the risk in those without. For clinical applications, however, it is more crucial to assess the absolute risks of individuals with and without a family history of disease. For the same degree of familial relative risk (explained, for example, by known genetic variants), much stronger stratification is possible for common diseases than for less common diseases. Furthermore, the utility of the PRS depends on other aspects of the disease, including information on the residual effects of family history (that is, the effects of family history that cannot be explained by known genetic variants) and other risk factors, as well as the available strategies for reducing risk or for early detection of the disease.

In summary, unbiased estimates of heritability can be useful for understanding the theoretical limits of genetic risk-prediction models. The clinical utility of models, however, depends on various other factors, including the absolute risk of diseases and the available strategies for disease prevention in the population.

Building absolute risk models

Throughout this Review, we emphasize the importance of evaluating absolute risks in order to determine the clinical utility of risk models. Thus, it is useful to begin with a broad framework for developing absolute risk models and then to describe specific steps for model building and evaluation using this general framework. We focus on an epidemiological framework for model building in which risks are quantified in terms of underlying age-specific incidence rates of diseases based on the proportional hazard model (BOX 1).

Box 1. ncidence-based model for absolute risk of diseases.

Models for evaluating absolute risk need to account for age, which is the strongest risk factor for many adult-onset chronic diseases. In epidemiological studies, disease risks are commonly modelled using the age-specific incidence rate based on the proportional hazard model35 of the following form:

I(a|Z)=I0(a)×exp(∑K=1KβkZk)

The model assumes that the conditional age-specific incidence rate of the disease, I(a | Z), defined as the probability of developing the disease at a particular age, a, given that a subject has been disease-free until that age, is given by the multiplicative effect of a set of risk factors, Z = (_Z_1,…,_Z_K), on the baseline hazard of the disease, (_I_0(a)). The set of variables in Z could include genetic and environmental risk factors, and their interaction terms. The associated hazard ratio parameters, exp(_β_k), quantify the corresponding effect sizes for individual factors, and the term:

is referred to as the underlying multivariate relative risk model.

Based on the above model, the probability that an individual who is disease-free at current age a will develop the disease over an age interval [_a, s+a_] can be defined as in REF. 113:

Ra,a+s=∫aa+sI(u|Z)exp(−∫au{I(v|Z)+m(v|Z)}dv)du

where m(v|Z) is the age-specific mortality from other causes. In other words, the absolute risk of the disease over a specified age interval is defined by the sum (over all ages within the interval) of the probability that the subject will develop the disease at a given age, u, given that the person remains disease-free and does not die from other causes until then.

The development of an absolute risk model requires the synthesis of data from different sources. Prospective cohort studies can be used for direct estimation of hazard ratio parameters using the Cox partial-likelihood framework35. Moreover, incident case– control studies can be used to approximate hazard ratio parameters based on odds ratios that can be obtained from logistic regression analysis36. Data from either representative cohort studies or population-based registries can be used to estimate the baseline rate of the disease35,113. For the application of models to general populations, it may be preferable to calibrate absolute risk models using disease rate information from population registries and the representative distribution of risk factors in the underlying population. The overall incidence rate of the disease, I(a), in a population is given by a weighted average of the covariate-specific incidence rate of the disease where the average is evaluated with respect to the underlying population distribution of the covariates. Mathematically, the relationship can be expressed as:

I(a)=I0(a)Ea{exp(∑K=1KβkZk)}

where the expectation, E, in general, needs to be computed with respect to the distribution of risk factor Z in the underlying population of subjects who are disease-free and did not die from other causes until age a. For relatively rare diseases, with fixed risk factors (such as single-nucleotide polymorphisms) that do not change over time and are unlikely to have large effects on either the disease or competing mortality, the distribution can be assumed to be constant with respect to age. Analogously, absolute rates of mortality from competing risks can be estimated from representative cohort studies and population registries.

The authors have developed and distributed a software tool, iCARE, that follows the basic steps described above for building absolute risk models by synthesizing information from different data sources.

Defining absolute risk using underlying models for disease incidence rates has numerous advantages over modelling in other scales. Prospective cohort studies can be used to directly estimate disease incidence rates and hazard ratio parameters after accounting for censoring due to loss to follow up or death35. Moreover, case–control studies can be used to obtain approximate estimates of the hazard ratio parameters under certain assumptions. Population-based incident case– control studies allow unbiased estimation of hazard ratios based on odds ratios that can be obtained from logistic regression analysis after adjusting for age using fine categories36. Case–control studies that include prevalent cases can lead to biased estimates of hazard ratio parameters if the risk factors for disease incidence are also related to survival following disease37. Case– control studies that do not follow a population-based design can suffer from other types of selection bias due to non-differential participation of subjects by both risk factor and disease status38. For common susceptibility SNPs, which have weak effects on risk and are typically not related to survival and the likelihood of study participation, estimates of odds ratios available from case–control studies are expected, in general, to provide a good approximation for the hazard ratio parameters.

The proportional hazard regression model for disease incidence provides a convenient way of building models for absolute risk by synthesizing data from various types of studies. These include cohort and case–control studies for the estimation of risk parameters and population-based registries for the estimation of underlying disease incidence and competing mortality rates.

Choice of scale for multivariate risk

The assumptions underlying the proportional hazard model (BOX 1) require scrutiny. The model assumes that the effects of the covariates (Z; BOX 1) are multiplicative (or additive after log transformation) with respect to the effect of age on the incidence rate of the disease. Similarly, if the covariate terms include only the main effects of individual risk factors, then the model implies that the effects of individual factors are multiplicative with respect to each other. The model can be extended to test for and incorporate interaction parameters that capture non-multiplicative effects between sets of risk factors.

Some alternative models for specifying disease risk merit attention. The logistic regression model, widely used to analyse case–control studies, specifies disease risk in the logit scale. For incident case–control studies, odds ratio parameters in logistic models, when finely adjusted for age, can be used to approximate hazard ratio parameters of the proportional hazard model36. Liability-threshold regression39, popularly used in statistical genetics literature, models the effect of the risk factors on an underlying, normally distributed liability score. The model assumes that a disease is manifested when the liability score exceeds a certain threshold and corresponds to the use of the probit link function.

The liability threshold model closely resembles logistic regression in its functional form and thus requires similar assumptions. For example, an assumption of the additivity of multiple risk factors in the probit scale indicates that their effects are approximately additive in the logit scale and vice versa40. The regression parameters across the two models, however, may not be directly comparable owing to differences in standardization with respect to underlying phenotype variance. In particular, case–control sampling affects the interpretation of regression parameters in the liability threshold model but not the interpretation of odds ratio parameters in the logistic regression model. However, because of similarities in their functional forms, it may be possible that risk scores (such as PRS) that are generated under one model can be transported into the other model after suitable calibration by scale factors.

Yet another approach to model disease risk could involve using the identity link function — that is, to model the effects of risk factors directly on the risk of the disease itself without any transformation. It has long been argued that testing for a departure from additivity under the identity link, referred to as additive interaction, can be useful for obtaining insights into the biological mechanisms of action of the risk factors, and also for assessing the public health impact of risk factor interventions41. Multivariate risk profiles generated by additive models under the identity link function can be very different from those under closely related proportional hazard, logistic and probit link functions. In particular, the absolute risk could increase (or decrease) much more rapidly with the increasing (or decreasing) number of risk factors under the latter types of models than under the identity link function42. Investigations of SNP-by-SNP and SNP-by-environment interactions using data from large GWAS generally suggest that the assumption of multiplicative effects is often adequate and an additive model under the identity link can be soundly rejected43–46.

In summary, proportional hazard models and closely related logistic regression models specify the risk of disease on a multiplicative scale. Assumption of multiplicative effects often provides reasonable initial models for specifying the joint effects of multiple risk factors.

Building a model for relative risk

Building a model of absolute risk first requires the development of a model for the multivariate relative risk (BOX 1) of the disease associated with a set of risk factors, termed Z (BOX 1). When simultaneously considering the risk associations of many different genetic markers, such as SNPs evaluated in GWAS, a parsimonious strategy could be to first develop a risk model for the SNPs through an underlying PRS variable and to then develop a model for the joint effects of the PRS and other risk factors. Such an approach could also be statistically efficient, as a model for PRS alone could be built based on data from GWAS, including multiple studies with very large sample sizes for which detailed data on environmental risk factors may not be available.

GWAS-PRS

Information from large GWAS provides an opportunity for the development of risk models that incorporate SNPs. A critical step towards this effort is the development of an optimal PRS defined by the combination of SNPs that yield the best predictive model for a given disease. GWAS heritability estimates for many diseases indicate that SNPs have significant potential for risk prediction using the underlying true PRSs that capture the precise effects of all the SNPs; however, such a model could be built only if an infinite amount of data was available. In practice, we can only hope to build an imperfect PRS owing to the imprecision associated with model building algorithms and imperfect tagging of the underlying causal variants by marker SNPs.

All algorithms for constructing PRSs have two essential elements. The first is a procedure for ‘variable selection’ to determine which SNPs need to be included in the model. The second is a procedure for the estimation of coefficients, or weights, that will be attached to the selected variables. Statistical imprecision in both of these steps can cause the predictive ability of the GWAS-PRS to fall short of that of the true PRS (BOX 2). Mathematical power analysis indicates that the challenge is particularly severe in GWAS because the total heritability could be distributed over thousands, and in some cases tens of thousands, of common SNPs each with extremely small effects47–51. Under such extreme polygenic architecture, selection of the true set of susceptibility SNPs for the model is particularly challenging, and the rate of improvement in the precision of the model, as a function of sample size, is expected to be slow (FIG. 3). The extreme polygenic architecture of many common diseases indicates that the predictive performance of the PRS will slowly improve in the future with increasingly large studies and will reach a plateau only after GWAS reach huge sample sizes that could involve hundreds of thousands of individuals.

Box 2. Risk distribution and discrimination with true and estimated PRS for a rare disease.

Let D denote the disease status for a rare disease and PRST denote the underlying true polygenic risk score (PRS), expressed in log-risk scale:

The parameter σ2 = Var(PRST) can be referred to as the heritability of the disease in the log-risk scale. If it can be assumed that PRST is distributed normally in the population, then the distribution of PRST in cases will also follow a normal distribution with the same variance (σ2) but with the mean shifted rightward by a value that is also equal to σ2 (see the figure, part a). In other words, the degree of separation in the distribution of PRST between cases and controls is determined by the heritability (σ2) itself. Thus, measures of the discriminatory ability of models, such as the area under the curve (AUC), have a one-to-one relationship with heritability8.

Now suppose that PRSE denotes an ‘estimated’ value of PRS that could be obtained from a model built from empirical studies. By definition, PRSE will be imperfect compared to PRST owing to various types of errors. For example, in a typical PRS that is built based on data from genome-wide association studies (GWAS), the errors could come from the inability of common SNPs to tag all underlying causal SNPs, and from statistical imprecision in algorithms of SNP selection and coefficient estimation owing to the finite sample size of current GWAS. The risk stratification ability of PRSE depends on the key quantity47:

where s2 = Var(PRSE) and c = Cov(PRSE, PRST).

In particular, if we assume that PRSE is normally distributed in the underlying population, its distribution in cases will also follow a normal distribution with the same variance but the mean now shifted by c instead of s2 (see the figure, part b). Intuitively, the covariance term c will increase as the PRSE includes more ‘signal’ terms that contribute to true genetic risk (PRST) irrespective of the inclusion of ‘noise’ terms that are unrelated to the PRST. However, inclusion of more noise terms will increase the variance of PRSE (s2) and will thus dilute the discrimination of the distribution between cases and controls.

Furthermore, as the true odds ratio of the disease is given by:

logPr(D=1|PRSE)/(D=0|PRSE)=c/s2×PRSE

a calibration factor c/s2 needs to be multiplied by PRSE if it is to be used as an unbiased estimation of risk. Once PRSE is calibrated, the variability of the estimated score is r2, which also determines its discriminatory ability (see the figure, part c). Adapted with permission from David Check, US National Institutes of Health.

Box 2

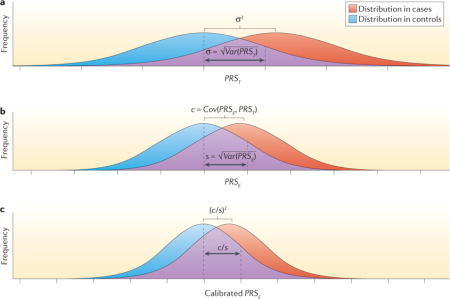
Figure 3. Effect-size distribution for susceptibility markers and implications for risk prediction.

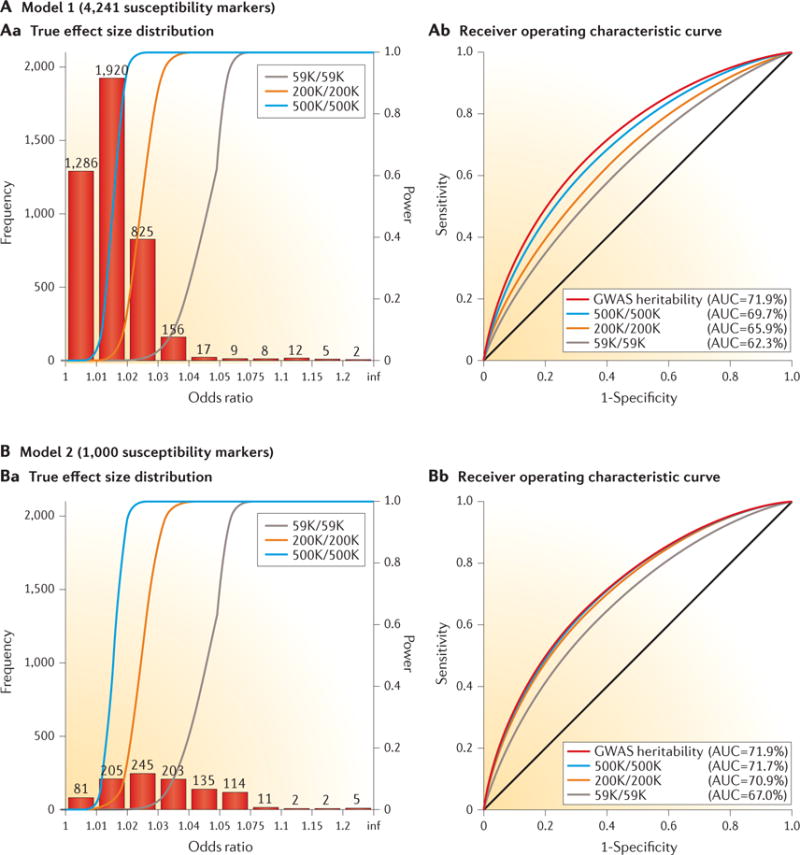
Figure 3

True effect-size distribution of individual single-nucleotide polymorphisms (SNPs) and predictive power of polygenic risk scores (PRSs) under two distinct models (model 1 (panel A) and model 2 (panel B)) for the genetic architecture of breast cancer. The total heritability explained by the additive effect of SNPs from genome-wide association studies (GWAS), termed narrow-sense GWAS heritability, is assumed to be the same (sibling relative risk ~1.4) between the two models, but the number of underlying susceptibility SNPs over which the heritability is dispersed is allowed to be different. The estimates of GWAS heritability and the value of M = 4,241 as the number of underlying, independent susceptibility SNPs are obtained empirically based on an analysis of effect-size distribution using summary-level results available from the DRIVE (discovery, biology, and risk of inherited variants in breast cancer) project of the Genetic Associations and Mechanisms in Oncology (GAME-ON) Consortium. Under this model for effect-size distribution (panel A), a single-stage GWAS study including 59,000 cases and an equal number of controls is expected to lead to the discovery of the same number of susceptibility SNPs for breast cancer as has been reported to date. The value of M = 1,000 is chosen to represent a hypothetical effect-size distribution where the same degree of GWAS heritability is explained by a smaller number of SNPs (panel B). In both models, it is assumed that the PRS is defined by the additive effects of SNPs reaching genome-wide significance (P < 5 × 10−8). The different coloured lines in panel Aa and panel Ba represent the power curve for the detection of SNPs at a genome-wide significance level as a function of effect size for studies of different sample sizes (numbers of cases/number of controls; K = 1,000). The different coloured lines in panel Ab and panel Bb show the expected receiver operating characteristic curves for PRSs that were built based on studies of different sample sizes and a PRS that can be built based on infinite sample size, thus explaining GWAS heritability. Comparison of panel Ab with panel Bb illustrates that when the number of underlying susceptibility SNPs is larger, the effect sizes are smaller, the average power of detecting individual susceptibility SNPs is lower, and the discriminatory ability of PRSs improves at a slower rate with sample size. AUC, area under the curve. Adapted with permission from David Check, US National Institutes of Health.

Incorporating disease association information for SNPs

Despite the inherent limitations of GWAS-PRS that are associated with sample size, it is worthwhile to investigate the optimal PRS that could be constructed based on a given set of GWAS data. The simplest and most popular approach is to select SNPs based on the significance of the individual association test statistics, and then weight the SNPs in the PRS according to the corresponding estimated regression coefficients, such as log odds ratio parameters from an underlying model. Many genetic risk-prediction studies48,52–59 have investigated the risk stratification ability of the PRSs that include independent SNPs reaching genome-wide significance levels in existing studies. These studies show that such SNPs, with the exception of those in the human leukocyte antigen (HLA) region associated with autoimmune disorders, typically provide small to modest discriminatory ability.

It may be possible to improve the predictive power of a PRS by the inclusion of additional SNPs that are below the genome-wide significance level. An inclusion threshold that is more liberal than the genome-wide significance level allows the contribution of ‘signals’ from additional susceptibility SNPs at the cost of adding noise from SNPs that are not truly associated with the disease (BOX 2). In theory, the optimal threshold in which the signal-to-noise ratio is balanced to yield the best predictive power depends on the sample size of the discovery GWAS and the genetic architecture of the trait47. In practice, the optimal threshold can be determined based on the performance of the model in an independent sample, or using cross-validation techniques. For many common complex diseases, such as certain cancers, type 2 diabetes and heart disease, both theoretical evaluation (based on inferred effect-size distributions) and empirical assessment (using large GWAS) suggest that the gain in predictive ability from an optimized threshold is likely to be modest at current sample sizes47. More notable gains have been observed for diseases like schizophrenia, bipolar disorder and multiple sclerosis, which are highly heritable and have an extremely polygenic architecture, possibly involving tens of thousands of susceptibility SNPs60–63.

Handling of correlated SNPs in the calculation of PRSs requires particular attention. Inclusion of correlated SNPs that do not contain independent signals can significantly reduce the predictive performance of models64. A common method for dealing with this problem is association-informed linkage disequilibrium (LD)-based pruning, which is implemented in the popular whole-genome association analysis toolset PLINK65. This method involves sorting SNPs based on the strength of association signals, then removing the SNPs that are in linkage with the strongest signal within LD regions. Typically, a fairly stringent threshold (for example, _r_2 < 0.05) is needed to remove the detrimental effects of correlation. Stringent LD-pruning, however, can also reduce the predictive power of PRSs by eliminating susceptibility SNPs that are in LD but contain independent association signals. Multivariate methods that allow the modelling of independent associations accounting for LD have been shown to improve the performance of PRS models in some settings66. In summary, building an optimal PRS based on GWAS requires careful consideration of sample size, the threshold for SNP selection, weight assignment for selected SNPs and the underlying linkage disequilibrium.

Incorporating external information

Incorporation of various types of external information, including pleiotropic, functional and annotation information, to prioritize SNPs may improve the predictive power of PRSs. A variety of closely related mixed models, Bayesian methods and penalized regression methods allow the incorporation of external information to inform ‘priors’ for effect-size distribution in the analysis of GWAS data67–70. Typically, in these methods, the log odds ratio association parameters are assumed to have a symmetric distribution with a mean of zero and the spread defined by one or more variance component parameter or parameters, depending on the complexity of the model. In these methods, the underlying prior allows ‘shrinkage’ of the estimated association coefficients of the SNPs towards the null value to provide a better trade-off between bias and variance, both of which contribute to PRS imprecision. The degree of shrinkage depends on the form of the prior. For example, although a single normal model for effect-size distribution imposes the same degree of shrinkage for all SNP coefficients, a two-component normal mixture model allows some coefficients to be shrunk to a lesser degree than others, to allow for the possibility that a fraction of SNPs have relatively large effect sizes69.

As the optimal shrinkage towards the null depends on the true nature of the effect-size distribution, no method that assumes a particular form of prior will perform most effectively for every genetic architecture. Empirical-Bayes type methods that allow data-driven flexible modelling of effect-size distributions can be expected to perform robustly across different settings. Information from pleiotropic analysis, functional annotation, and expression- and methylation-quantitative traits loci can all be incorporated in a structured manner to form differential priors for the associations of different SNPs. Various recent studies have demonstrated that the use of well-informed priors, including information on both pleiotropic and functional annotation, can accelerate the discovery of susceptibility loci compared to more agnostic approaches that have dominated GWAS analysis to date71–74. In addition, recent studies have shown that for some psychiatric disorders and two autoimmune diseases (Crohn disease and ulcerative colitis), each with a strong genetic correlation, pleiotropic information can substantially improve the performance of genetic risk prediction models for individual traits75,76. Although recent heritability partitioning studies have demonstrated that specific functional categories of SNPs are strongly enriched for common diseases77, the impact of functional annotation on the performance of polygenic risk prediction models needs extensive empirical investigation in the future, especially as sample sizes increase and more refined external information becomes available.

Modelling joint effects

Once an optimal PRS has been developed, the next task is to develop a model for hazard ratios associated with the joint effects of the PRS and other risk factors for a disease. This requires the characterization of risk (hazard ratios) associated with individual factors and the exploration of possible interactions (non-multiplicative effects) between these factors. Ideally, data from prospective cohort studies should be used to estimate the risk associated with lifestyle, behavioural and environmental factors. Such estimates can be affected by various types of selection and recall bias when data from case–control studies are used. However, carefully conducted population-based incident case– control studies, such as those nested within well-defined cohort studies, could provide valid estimates of the risk associated with such factors. Furthermore, tests for multiplicative interactions, which are less sensitive to selection bias78, may be performed based on broader sets of studies. Typically, logistic regression methods are preferred for the evaluation of multiplicative interactions. For case– control studies, if it can be assumed that environmental risk factors are independent of the SNPs in the underlying population, then case-only and related methods can be used to increase the power of tests for gene– environment interactions79–81. To date, post-GWAS epidemiological studies of gene– environment inter actions have generally reported multiplicative joint associations between low-penetrant SNPs and environmental risk factors, with only a few exceptions.

Accounting for family history in risk models is important, as a PRS typically can explain only a fraction of the disease risk associated with family history. In models developed for the general population, family history is often modelled as a simple binary variable that indicates the presence or absence of the disease among first-degree relatives of study subjects. The use of more extended family history information, including age of disease onset, could improve the risk stratification ability of models especially in clinical settings that involve counselling of highly affected families82,83. Furthermore, models in such settings can be improved by incorporating information on carrier status for rare high-penetrant mutations in major genes — for example, mutations in BRCA1 and BRCA2 for breast and ovarian cancers. Although the same basic framework as described above can be used for the development of such extended models, data from affected families, in whom the mutations are relatively common, will be needed to reliably estimate hazard ratios associated with these mutations and explore their interactions with other factors, including PRS.

It is important to note that tests for multiplicative interactions, or any other form of interaction, may not be significant because of insufficient power. Model misspecification owing to the omission of gene–gene or gene–environment interactions, although unlikely to have a major impact on discriminatory ability84, can affect the calibration performance of models. Therefore, goodness-of-fit tests should be performed when assessing the adequacy of models. As knowledge of risk estimates is likely to be most relevant for subjects at extreme levels of high or low risk, evaluating the adequacy of risk models at the extremes of risk requires special attention for clinical applications43.

In summary, the development of models for the joint effect of PRS and other risk factors requires characterization of the risk associated with individual factors, exploration of interactions and testing of the goodness of fit of the selected models. Data from various types of studies, including cohort and case–control studies, and affected families could be used, but careful consideration is needed to avoid the effects of selection or recall biases.

From relative to absolute risk

As described earlier, the proportional hazard regression model provides a convenient framework for building models for absolute risk. Once a model for relative risk is built, evaluation of absolute risk requires estimation of the baseline hazard, which is the incidence rate of the disease associated with a baseline risk profile, with respect to which relative risks are estimated. Data from either representative cohort studies or population-based registries can be used to estimate the baseline rate from the underlying overall rate of disease (BOX 1).

When evaluating absolute risk, it is important to adjust for competing risks of mortality, especially at older ages when the risk of dying from other causes could be high; typically, overall mortality rates are used, assuming that the disease and risk factors being studied have modest effects on overall mortality within a population. More sophisticated risk-factor-dependent models for mortality could also be built from cohort studies and could be incorporated into models for risk prediction for specific diseases85.

Whenever possible, the use of disease and mortality rates available from population-based registries is recommended to ensure the generalizability of absolute risk models to the underlying populations. If relative risks could be assumed to be applicable to different ethnic populations, then models for absolute risk could be quickly adapted by simply incorporating registry-based information on the underlying disease incidence and mortality rates. Furthermore, population-based registries can be used to assess secular trends in disease incidence and mortality rates, and to appropriately update absolute risk models over time.

Risk model evaluation

Once a model for absolute risk has been built, both its calibration and risk stratification ability must be evaluated.

Evaluation of model calibration

Calibration of a model refers to its ability to produce unbiased estimates of risk for subjects in different risk factor profiles in the underlying population. Model calibration needs to be evaluated in a representative sample that is independent of the studies that contributed to the model building procedure. Ideally, prospective cohort studies are needed to compare the observed and predicted number of incident cases over specified time intervals. Subjects can be classified into strata based on their predicted risks, and the observed and expected number of cases can be compared within these different strata to evaluate the calibration of models at different levels of risks. Graphical displays for visual inspection and formal tests for goodness of fit86 can be used to assess model calibration. Nested case–control studies, in which subjects are sampled from well-defined cohorts, can also be used in calibration studies, as sampling weights can be used to recover the underlying disease incidence rate in the cohort.

Absolute risk models may be miscalibrated in a number of different ways, resulting in over- or underestimation of risks. A model may produce an unbiased estimate of the overall risk of the cohort, but it may be miscalibrated for certain risk strata. Such a pattern could arise if the baseline risk has been estimated by calibrating the model using a representative disease rate for the overall population, but the underlying model for relative risk has been misspecified. By contrast, a model may consistently over- or underestimate the risks for different risk strata if the underlying disease incidence rate that is used is not representative of the population for which the prediction is desired. A recent study, for example, found that a number of different risk calculators for heart disease that were developed based on older cohorts overestimated the disease risk in individuals from a multi-ethnic, contemporary cohort87.

As the calibration of models can vary by ethnic and demographic factors, birth cohort and calendar time, it is important that validation studies for established risk models continue to be conducted for relevant populations (that is, those groups for which the models may be used in clinical applications). It is also important that models are developed in a flexible way so they can be easily updated using new information on risk factors and disease incidence rates as it becomes available. As a single study may not have all the relevant information, keeping models up to date in the future will require synthetic model-building procedures that allow the integration of information from multiple data sources.

Assessing risk stratification

Once a model is found to be valid in assessing risk — that is, well calibrated for an underlying population of interest — it needs to be further assessed for its utility in clinical or public health applications. As noted earlier, the clinical utility of a well-calibrated model generally depends on how much spread of risk the model can provide for the underlying population of interest. However, the exact criteria based on which the utility of the model should be evaluated, on its own or relative to others, depend heavily on the clinical application under consideration.

Historically, many studies have assessed models based on their discriminatory ability — that is, how much separation they can produce in the distribution of risks among individuals who will develop the disease in the future compared to those who will not (BOX 2). The area under the curve (AUC), which is defined as the probability that a randomly selected individual with a disease will have a higher risk than a randomly selected individual without the disease, is a commonly used summary statistic for assessing the discriminatory ability of models. AUC values of 50% and 100% correspond to models with no and perfect discriminatory power, respectively. For most common complex diseases, common susceptibility SNPs identified through GWAS alone provide low (AUC < 60%) to modest (AUC = 60–70%) discriminatory ability. Estimates of GWAS heritability indicate that common SNPs alone may not lead to models with very high discriminatory ability (AUC > 80 or 90%) for common complex diseases; however, substantial scope for improvement remains.

As the AUC does not have a direct clinical interpretation, researchers have recently attempted to define alternative, more clinically relevant criteria for evaluating risk models. For applications that target high-risk individuals for screening, one may evaluate the proportion of populations and the proportion of future cases that may be identified, based on a model, as exceeding a certain risk threshold88,89. To maximize benefit and minimize harm associated with unnecessary screening and other procedures, an ideal model should be able to identify a small fraction of the overall population that will give rise to the majority of future diseases. Models with modest discriminatory ability, such as those involving PRS for breast cancer52, can identify a substantial fraction of the population that could be at meaningfully higher risk than the general population. However, the majority of cases in a population can still arise outside the groups identified as being at high risk, unless the discriminatory ability of the underlying model is high90.

To evaluate the added value of new risk factors incorporated into a model, it has been increasingly common to carry out an ‘assessment of reclassification’. Specific risk thresholds that affect clinical decision making may be used to cross-classify subjects based on risk strata that have been assigned according to an existing model and a new model. Several types of net reclassification indices (NRIs) have been proposed to quantify the degree to which the new model can provide more accurate classification — that is, shift the disease cases to higher-risk categories and the controls to lower-risk categories91,92. These summary measures, however, are generally abstract in nature and do not directly relate to any measure of net benefit achieved by the use of a new model at a population level. Measures of NRI have also been proposed for comparison of models in the absence of pre-specified risk thresholds; however, this approach has faced severe criticism because of its tendency to produce false-positive results regarding improved performance of models with additional factors93,94. In summary, the clinical utility of models depends on the degree of risk stratification they can produce for the population, and the optimal criterion for evaluating risk stratification depends on the clinical application under consideration.

Case studies

In this section, we discuss case studies that illustrate the potential value of polygenic risk prediction in stratified or precision approaches to disease prevention. For this purpose, we have chosen four diseases with varying lifetime risks in the US population, varying levels of knowledge on risk factors and with different strategies available for primary prevention (that is, prevention of the development or delay of the onset of disease) and secondary prevention (that is, strategies for early detection and prevention of disease progression). Each study examined genetic risk based on previously validated SNPs that have achieved genome-wide significance. Supplementary information S1 (table) shows the study designs, the methods used in different steps for model building and validation, and the criteria used for evaluating the clinical utility of the models.

Coronary heart disease

Coronary heart disease (CHD) is a common but preventable disease in many instances, as many causes are known and can be modified. Advice to adopt a healthy lifestyle (for example, a healthy diet, healthy weight, low or no alcohol use, adequate physical exercise and avoidance or cessation of smoking) to lower the risk of CHD applies to the general population, as it has clear health benefits with regard to multiple diseases and has no associated harms. In this context, risk assessment could be used to identify individuals at elevated risk who could benefit most from these lifestyle changes or from initiating preventive treatment with statins. For instance, the joint American College of Cardiology and American Heart Association Task Force recommend treatment with statins to reduce low-density lipoprotein (LDL) cholesterol levels for the primary prevention of CHD in individuals with a 10-year risk of CHD that is 7.5% or higher95.

The potential value of knowledge on genetic risk was nicely illustrated by a recent study that reanalysed several statin prevention trials by risk stratification based on a 27-SNP PRS96. The study showed that taking statins reduces the absolute risk of CHD to a greater extent in individuals at higher compared to lower polygenic risk. For instance, after 6 years of follow up in the ASCOT (Anglo-Scandinavian Cardiac Outcomes Trial) primary prevention trial, the risk of developing CHD was reduced following statin therapy from 3.0% to 1.9% (1.1% absolute risk reduction (ARR)) among individuals in the lower quintile of genetic risk, whereas it was reduced from 6.6% to 3.6% (3.0% ARR) among individuals in the highest quintile of genetic risk (FIG. 4). This translates into an almost threefold reduction in the number of people needed to prevent one CHD event in high-versus low-risk groups. Estimates of ARR can be affected if the underlying incidence rate of disease in the studies is not representative of the general population. To assess the potential risk reduction achievable for the general population, one may use hazard ratio parameters associated with the joint effect of PRS and treatment categories from these trials, and then obtain estimates of absolute risk by calibrating the model using external population-based estimates of disease incidence rate.

Figure 4. Role of polygenic risk in determining absolute risk reduction for coronary heart disease and bladder cancer achievable by modification of environmental risk factors.

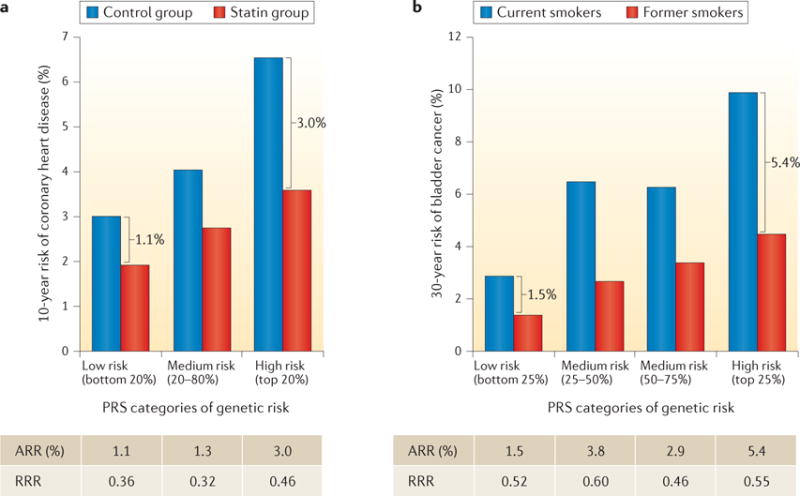
Figure 4

Ten-year risk of coronary heart disease associated with statin therapy (panel a) and 30-year risk of bladder cancer associated with smoking status (panel b), across genetic risk categories defined by the polygenic risk score (PRS) distribution. Brackets indicate the absolute risk reduction (ARR) between treatment or exposure groups for subjects in different PRS categories. The tables show the ARR and relative risk reduction (RRR) between treatment or exposure groups (panel a, statin versus control group; panel b, former versus current smokers), across PRS categories. The studies illustrate that subjects at higher polygenic risk may benefit more (that is, have a greater reduction in absolute risk) from risk-reducing interventions, such as statin therapy or smoking cessation. Data in panel a from REF. 96. Data in panel b from REF. 101, American Association for Cancer Research.

Breast cancer

Breast cancer is common in women in the United States and other Western countries, and its incidence rates are now rapidly increasing in many developing countries. There are multiple risk scores for predicting breast cancer risk in the general population; however, their discriminatory accuracy is limited and additional risk factors usually result in small improvements in the AUC97.

A recent study evaluated the risk stratification ability of a 77-SNP PRS for breast cancer52. Instead of evaluating the AUC, the study examined a related but more meaningful measure of the value of risk models — the ability to identify individuals in the population who have crossed clinically relevant risk thresholds. For instance, women in the United Kingdom are invited to start mammographic screening when they turn 47 years old, which corresponds to a 2.4% 10-year risk threshold, as this is the average risk for women at this age. The study found that women in the top 10% of genetic risk, according to the 77-SNP PRS, would reach this risk threshold in their early 30s, whereas women in the bottom 10% of the polygenic risk would remain below this threshold throughout their lifetime (FIG. 5). Thus, information on genetic risk, in addition to family history, is more effective than an age-based criterion in guiding decision making on when mammographic screening should be initiated98. Another recent study used published estimates of odds-ratio association parameters for SNPs and non-genetic risk factors to develop a ‘synthetic’ risk model under the assumption of multiplicative effects. This study showed that risk models could also be relevant for communicating risks and benefits to individuals regarding decision making, such as taking menopausal hormone therapy or preventive endocrine therapies99. Both of these models, however, require further evaluation of model calibration in independent prospective cohort studies.

Figure 5. Role of polygenic risk in determining the optimal age of initiation for screening of breast and colon cancers.

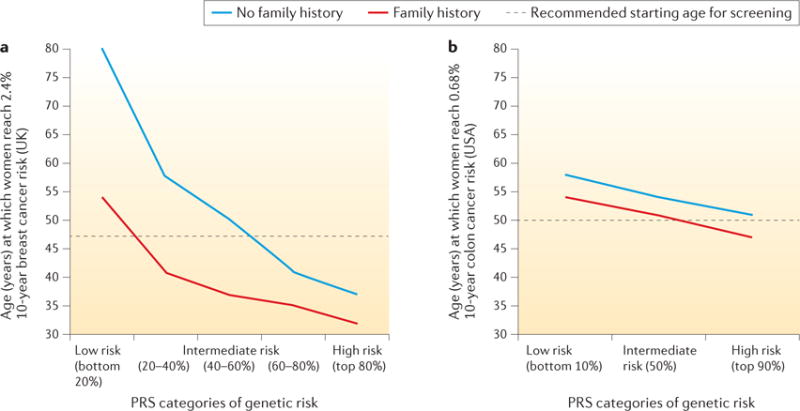
Figure 5

Age at which the risk of developing breast cancer reaches 2.4% (panel a) or the risk of developing colon cancer reaches 0.68% (panel b) over the next 10 years, for women at different levels of polygenic risk, with and without a family history of the disease. The risk levels of 2.4% and 0.68% correspond to the average population 10-year risk of developing each disease for women at the currently recommended starting ages for screening in the countries where the original studies were conducted (that is, 47 years old for breast cancer in the United Kingdom, and 50 years old for colorectal cancer in the United States). The studies illustrate that the risk threshold for screening is reached at earlier ages for subjects with higher genetic risk, defined by the polygenic risk score (PRS) and a family history of the disease. Data in panel a from REF. 52. Panel b adapted with permission from REF. 53, Elsevier.

Colorectal cancer

The US Preventive Services Task Force100 recommends colorectal cancer (CRC) screening for men and women from the age of 50 to 75; enhanced screening is recommended for those at elevated risk owing to family history of CRC, inflammatory bowel disease or suspected hereditary CRC syndromes. One CRC study investigated the utility of 27 SNPs, together with information on family history and endoscopy records, to guide the recommendation of screening53.

The study showed that, despite its low discriminatory ability (AUC < 60%), risk determined by the 27-SNP PRS in combination with family history can have a substantial impact on the age at which individuals reach the average absolute risk of a 50-year-old individual; this threshold was reached 10 years earlier for individuals at the top 10% of genetic risk (42 years in men and 47 years in women) than for those at the bottom 10% of genetic risk (52 years in men and 58 years in women) (FIG. 5). The risk stratification ability of PRSs for CRC is currently lower than that for breast cancer because of the much larger number of SNPs associated with the latter condition. Identification of additional SNPs, together with consideration of known environmental risk factors, can be expected to improve the risk stratification ability of CRC risk models in the future. An improved estimation of the risk of developing CRC would allow individuals to make more informed decisions on CRC screening, aided by the advice of their doctors. Undergoing screening is a personal decision that needs to take into account the potential benefits of early detection as well as the potential costs, such as the potential complications of colonoscopy.

Bladder cancer

In contrast to breast and colorectal cancers, bladder cancer is relatively uncommon with a very strong environmental causal component — primarily, cigarette smoking and occupational exposures — and there is no existing screening programme at the population level. Therefore, the most effective means of prevention are smoking cessation and occupational safety measures.

A recent study evaluated whether the impact of smoking prevention and/or cessation on bladder cancer risk could be different for subjects with different genetic risks, as defined by a PRS that used information from 12 genetic variants (11 SNPs and 1 deletion)101. The study showed that the potential benefit from smoking cessation, in terms of a 30-year ARR, is substantially more pronounced among individuals with higher genetic risk than those with lower genetic risk (FIG. 4). By contrast, measures of relative risk reduction (RRR) were similar for subjects in the top and bottom groups of genetic risk, illustrating the value of absolute risk measures in the context of prevention. In particular, ARR estimates indicated that 8,200 cases of bladder cancer could be prevented if smoking cessation occurred in 100,000 men in the upper PRS quartile, whereas 2,000 cases would be prevented by a similar effort in the lowest PRS quartile. Thus, these analyses indicate that genetic information could potentially be used for targeted smoking cessation programmes that are not applicable to the whole population — for example, because of associated costs. However, the authors also noted that, before making any recommendations, the impact of genetic stratification on other smoking-related diseases, such as lung cancer and cardiovascular diseases, should be considered along with the acceptability and ethical aspects of using genetic information in public health interventions.

Future directions

Future polygenic risk models will need to include disease susceptibility variants that have a wide range of allele frequencies, including common, low-frequency and rare variants. Clearly, rare and high-penetrant variants in known major genes, such as those in BRCA1 and BRCA2, will have an important role in determining the disease risk of individuals in highly affected families. In the near future, large-scale sequencing and imputation-based association studies will provide a more comprehensive assessment of the role of rare and low-frequency variants that may confer more moderate risk to diseases. Although the number of discoveries of these types of variants has been quite limited to date102–104, some studies indicate that rare and low-frequency variants have the potential to explain a substantial fraction of the heritability and, thus, variation of disease risks in the general population105. The underlying genetic architecture of complex diseases with respect to rare and low-frequency variants is likely to be as polygenic as has been observed for common variants. Therefore, studies of very large sample sizes will be required for the discovery of sufficiently large numbers of such variants to make a meaningful contribution to genetic risk prediction models.

Unlike genetic variants, environmental risk factors can change over the lifespan of individuals. Thus, repeated measurements of environmental risk factors or risk biomarkers will be needed to provide a risk assessment for diseases associated with both long-term average exposure levels and trends in exposure levels over time. Prospective cohort studies with longitudinally measured risk factor data will be needed for the development of dynamic models for risk prediction. Research is also needed on statistical methodology for the development, validation and application of risk models with time-dependent risk factors.

Improvements in models, through the incorporation of polygenic risk and possibly other predictive factors, to identify people at different levels of risk for developing diseases, could be translated into improvements in primary and secondary prevention by tailoring interventions according to risk. However, important questions will need to be addressed on how this approach could work in practice within the current health systems106. This will require: addressing organizational, legal and ethical factors that affect risk perception; acceptance and adoption of new risk-stratified programmes that use genetic information107–109; identifying the optimal service delivery mechanisms, including (but not limited to) cost-effectiveness and cost–benefit evaluations of alternative implementation plans110,111; educating and training health professionals in developing new risk communication tools and facilitating the implementation of risk-based strategies of intervention112; and conducting feasibility studies for implementation plans and, when possible, randomized trials to directly evaluate the impact of new programmes on health outcomes.

Supplementary Material

Supplemental Table

Acknowledgments

The research was supported by intramural funding from the National Cancer Institute, which is part of the US National Institutes of Health, and a Bloomberg Distinguished Professorship endowment from Johns Hopkins University.

Glossary

Penetrance

The proportion of individuals in a population with a genetic variant who develop the disease associated with that variant. Common single-nucleotide polymorphisms (SNPs) are referred to as low-penetrant, as risk alleles typically confer modest risk

Polygenic disease

A disease caused by a large number of underlying susceptibility genes

Prospective cohort studies

Studies that collect information on potential risk factors (based on questionnaires, devices and biological samples) in a sample of healthy individuals and then longitudinally follow them to record future disease incidence. Information on risk factors can be updated longitudinally over time

Heritability

The proportion of phenotypic variation attributed to genetic variation among individuals in a population

Polygenic risk score

(PRS)A score for predicting disease risk, calculated as the weighted sum of risk alleles with the weights specified by association coefficients

Ascertainment

Non-random selection of study participants, often arising in genetic studies owing to the selection of subjects based on personal and/or family history of disease

Ethnically admixed samples

Samples from subjects who have inherited genetic materials from two or more previously separated populations

Confounding

A false association between a disease and an exposure caused by the presence of a risk factor for the disease that is correlated with the exposure

Case–control studies

Studies that sample subjects with and without a disease and collect information on potential risk factors in a retrospective fashion

Incidence rates

(Also known as hazard rates). The rates at which new diseases are observed in a population during a specific time interval (for example, between specific ages)

Proportional hazard model

A model for incidence rate that assumes a multiplicative effect of risk factors on the age-specific incidence rate of a disease

Hazard ratio

The ratio of hazard rates (also known as incidence rates) between groups of subjects with different risk factor profiles

Incident case–control studies

Case–control studies that aim to recruit representative samples of new cases that arise in a population during a specified time period

Odds ratios

Quantitative measures of the strength of association between a binary disease end point and risk factors that can be estimated by logistic regression models

Prevalent cases

The number of individuals with a disease condition in a population at a given time point

Selection bias

Bias in risk estimates due to non-random selection of study participants. Case–control studies can be particularly prone to selection bias, as the likelihood of participation may be affected by both disease status and risk factor history

Logit

The transformation log{p/(1–p)} where p is the probability of disease occurrence in a population

Liability score

A score that represents the underlying progression of a disease through the accumulation of risks on a continuous scale. The risk of binary disease outcomes can be modelled by assuming the existence of an underlying, normally distributed liability score that leads to the manifestation of disease when it exceeds a threshold

Probit

The transformation Φ−1(p) where Φ−1 denotes the inverse of the cumulative distribution function for a standard normal random variable and p is the probability of disease occurrence in a population

Additive interaction

The presence of non-additive effects of multiple risk factors on the risk of a disease. Absence of additive interaction indicates that the risk difference parameter associated with one factor does not vary with that of other factors

Genome-wide significance

A stringent level of statistical significance, often set at p − val = 5 × 10−8 for genome-wide association studies (GWAS) of common variants, for the avoidance of false positives

Linkage disequilibrium

(LD). The non-random association of alleles at different loci, frequently measured by _r_2, the square of the genotypic correlation between two single-nucleotide polymorphisms (SNPs)

Pleiotropic analysis

Analysis to identify variants associated with two or more distinct phenotypic traits

Recall bias

Bias in risk estimates that could arise in case–control studies owing to differential recall or reporting of disease status by study participants

Multiplicative interactions

Presence of the non-multiplicative effects of multiple factors on the risk of a disease. Absence of multiplicative interaction implies that the risk ratio parameter associated with one factor does not depend on that of the other factors

Footnotes

Competing interests statement

The authors declare no competing interests.

SUPPLEMENTARY INFORMATION

See online article: S1 (table)

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Table