Strong triaxial coupling and anomalous Poisson effect in collagen networks (original) (raw)

Significance

Networks of collagen fibers are the primary mechanical component of the extracellular matrix of many soft tissues. In common pathological and physiological conditions, collagen networks experience a combination of multiaxial and shear deformation modes. Here, we show that the fibrous nature of the extracellular matrix leads to strong coupling between these modes due to bending, buckling, and stretching of the fibers. We have developed a 3D framework to describe the unusual nonlinear mechanics of these networks, in particular, the abnormally large lateral contraction and concomitant stiffening when stretched. Our model can guide improved design of engineered tissues for regenerative medicine and identify the mechanisms of pathological stiffening of extracellular matrices and their interactions with cells in cancer and fibrosis.

Keywords: fibrous matrices, matrix realignment, 3D cell traction force microscopy, tissue swelling

Abstract

While cells within tissues generate and sense 3D states of strain, the current understanding of the mechanics of fibrous extracellular matrices (ECMs) stems mainly from uniaxial, biaxial, and shear tests. Here, we demonstrate that the multiaxial deformations of fiber networks in 3D cannot be inferred solely based on these tests. The interdependence of the three principal strains gives rise to anomalous ratios of biaxial to uniaxial stiffness between 8 and 9 and apparent Poisson’s ratios larger than 1. These observations are explained using a microstructural network model and a coarse-grained constitutive framework that predicts the network Poisson effect and stress–strain responses in uniaxial, biaxial, and triaxial modes of deformation as a function of the microstructural properties of the network, including fiber mechanics and pore size of the network. Using this theoretical approach, we found that accounting for the Poisson effect leads to a 100-fold increase in the perceived elastic stiffness of thin collagen samples in extension tests, reconciling the seemingly disparate measurements of the stiffness of collagen networks using different methods. We applied our framework to study the formation of fiber tracts induced by cellular forces. In vitro experiments with low-density networks showed that the anomalous Poisson effect facilitates higher densification of fibrous tracts, associated with the invasion of cancerous acinar cells. The approach developed here can be used to model the evolving mechanics of ECM during cancer invasion and fibrosis.

The elastic modulus, strain–stiffening, and mechanical relaxation timescale of the extracellular matrix (ECM) regulate cellular behaviors such as differentiation and spreading (1–3), as well as the susceptibility of cells to infection by bacterial pathogens (4), and the response of cells to drugs. Mechanical cues and chemical signals are among the key factors that influence the migration of cells. Many cell types migrate toward stiffer regions of a substrate (5, 6) and follow the direction of fiber alignment (7, 8). The characterization and modeling of the mechanics of collagen matrices are important for understanding the interaction between invading cancer cells and the tumor microenvironment, and the relation between mechanosensing and matrix biosynthesis in fibrosis, as well as tuning the cellular microenvironment in tissue engineering applications. Most previous microstructural studies and constitutive models of ECM mechanics have focused on either the uniaxial, biaxial, or shear loading of the fibrous ECMs, whereas fiber networks physiologically experience combinations of these modes of mechanical loading. For instance, large Poisson effects are involved in fiber densification at collagen tracts, which promote the invasion of cancerous acinar cells (9). Moreover, factors such as overexpression of hyaluronic acid in cancerous tissues cause swelling in the ECMs of tumors (10, 11). In this state, the swelling of ECM is accompanied by the triaxial tension of the fiber networks and alters the mechanics of fibrous ECMs (12). Understanding the behavior of fibrous ECMs in multiaxial loading will help to elucidate the mechanobiology of cells in both healthy and diseased tissues.

Reconstituted collagen type I gels have been extensively used as a model system in the study of ECM mechanics and mechanobiology. Previous studies have found that in shear deformation, collagen networks behave as linearly elastic materials up to a certain threshold of strain. After the threshold, the networks strain–stiffen, following an exponential stress–strain behavior (13), signified by a power-law relationship between the differential modulus and shear stress with an exponent of 1.0. Recent experiments and computational modeling of collagen-mimetic disordered lattices showed that the stiffening exponents might differ from 1.0, depending on the conditions of polymerization and network connectivity (14). Strain–stiffening behaviors were also reported in uniaxial stretch tests (15). Reorientation of collagen fibers toward the direction of stretching, their alignment, and a transition from fiber bending to stretching have been described as the mechanisms underlying strain–stiffening in shear and uniaxial stretch tests (13, 16). Reconstituted fiber networks (17–19) and collagen-rich tissues such as tendons (20) and cartilage (21) exhibit large Poisson effects in stretch tests. In comparison with the response to tensile loads, collagen networks are orders of magnitude softer and exhibit negligible Poisson effects in compression tests (22). Equibiaxial tests and axial/shear tests have demonstrated synergistic stiffening of the networks under the application of a combination of loading modes (23). Previous biaxial tests also indicate that collagen-rich tissues such as the skin and blood vessel walls are stiffer in biaxial stretch than uniaxial stretch (24, 25). Coupling of multiaxial and shear loading and triaxial deformation of the networks, however, have not yet been the focus of modeling and experimental studies. Furthermore existing models of ECM mechanics (26–28), used in models of cancer invasion (29, 30) and fibrotic diseases (31, 32) do not account for the coupling of the axial modes of deformation and the nonlinear apparent Poisson ratios, larger than 1 (17–19).

The present paper describes the mechanisms of the triaxial deformation of fibrous networks, including the coupling of the modes of deformation and the large apparent Poisson ratios of collagen networks and its variation with changing collagen concentration. Microstructural fiber network models are presented to explain the stiffening of the networks in triaxial and biaxial loading and the Poisson effect. The effect of multiaxial loading on shear stiffness is described, and the influence of network pore size on multiaxial coupling and Poisson effect is reported. A coarse-grained constitutive law is developed for collagen networks to describe the pore size-dependent coupling of the multiaxial modes of deformation and Poisson effect at the scale of interacting cell clusters. Finally, two applications of the theoretical models are explored: the density-dependent Poisson effect observed in collagen matrices deformed by cancerous mammary acini, and a drastic increase in the apparent stiffness of thin collagen networks in extensional rheology tests.

Results and Discussion

Pore Size Dependence of the Anomalous Poisson Effect and Decrease of the Threshold Strain of Stiffening in Multiaxial Loading.

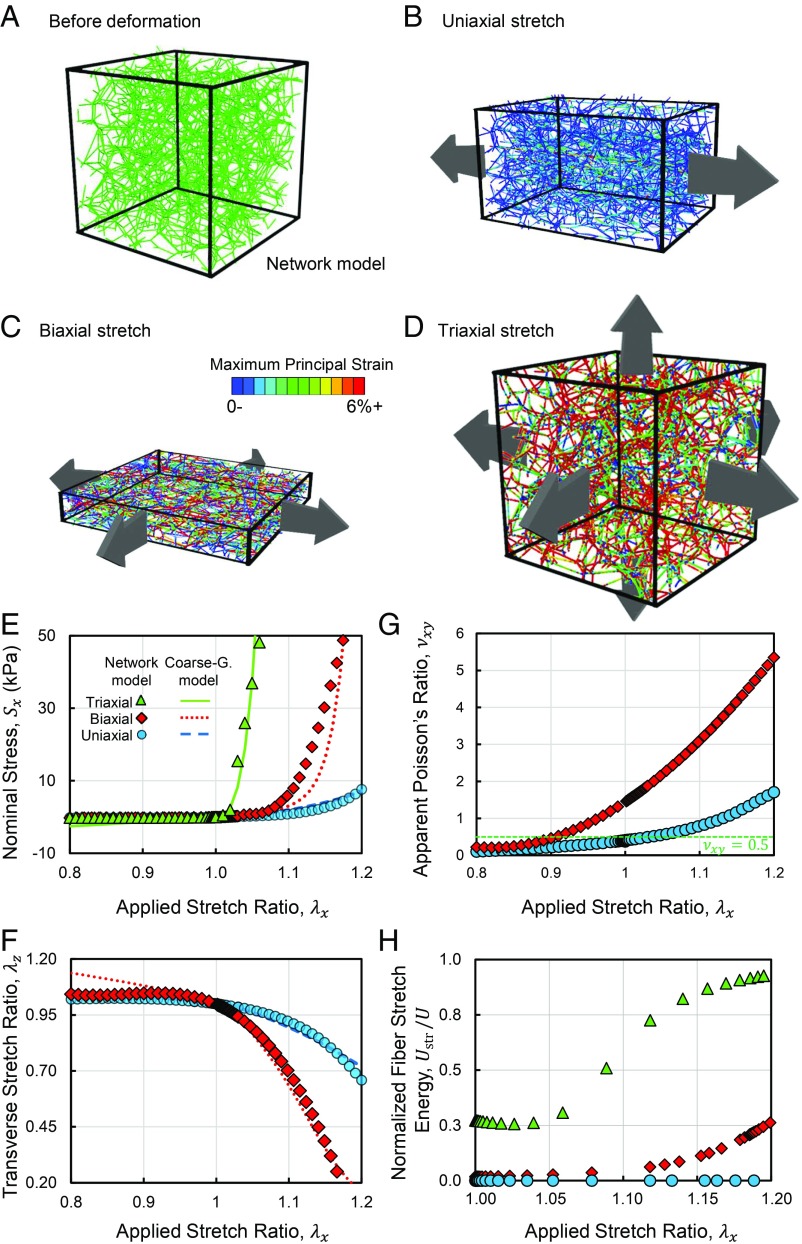
We began by studying the microstructure of collagen networks in uniaxial, biaxial, and triaxial deformation using a 3D fiber network model, consisting of connected elastic filaments (Fig. 1 A_–_D). The network was stretched in displacement-controlled uniaxial tests as it was free to contract in the directions transverse to loading. As expected, in the uniaxial stretch tests, where the network was stretching only in one direction, a linear stress–strain response was initially observed that later transitioned to an exponential strain–stiffening behavior (Fig. 1_E_, blue circles). During uniaxial tension, fibers bent and reoriented toward the direction of the applied stretch, eventually leading to fiber alignment. Variations of the distribution of the orientation of fibers in the tests with different modes of loading are marked on the unit spheres shown in SI Appendix, Fig. S1. Uniaxial tensile deformation was accompanied by contraction of the network in directions transverse to loading (Fig. 1_F_, blue circles). The apparent Poisson ratio, νxy, started from 0.4, below the limit of 0.5 for isotropic materials, and increased to 1.7 at an applied stretch of 1.2 (Fig. 1_G_). The apparent Poisson ratio was calculated as νxy=(1−λy)/(λx−1), where λx and λy denote the stretch ratios in the extension and transverse directions, respectively (33, 34). The large apparent Poisson ratios of the networks indicate a decrease of sample volume during uniaxial extension. The network exhibited a smaller Poisson effect and strain-dependent change in stiffness in compression tests compared with tension (Fig. 1 E and G and SI Appendix, Fig. S2). The stiffer network response in multiaxial deformation was accompanied by a higher stretching of individual fibers, quantified using the stretch energy of fibers (Fig. 1_H_ and SI Appendix, Fig. S2). Because the fibers are long and thin, they are softer in bending compared with stretching, rendering the networks stiffer in the presence of more fiber stretching.

Fig. 1.

Fig. 1.

The early onset of triaxial and biaxial stiffening of fibrous networks is accompanied by greater stretching of individual fibers compared with bending and rotation. Snapshots of the fiber network model (A) before loading and after (B) uniaxial tension, (C) equibiaxial tension, and (D) triaxial tension. The network snapshots show the microstructure of the network and the anomalous Poisson effect in uniaxial and biaxial deformation. A_–_D visualize the difference in the microstructural evolution of fiber reorientation, realignment, stretching, and buckling in the various modes of loading, quantified in Figs. 1_H_ and 2_D_, and SI Appendix, Fig. S2. In A, all fibers are colored green, whereas in B_–_D fibers are colored by maximum principal strain. (E) Stress versus stretch response of the fiber networks in uniaxial, equibiaxial, and volumetric tension and compression. (F) The stretch ratio in the transverse direction in uniaxial and biaxial tension and compression. (G) The apparent Poisson ratios of the networks are smaller than 0.5 for the isotropic networks but grow larger than 1 in the case of the anisotropically deformed networks. The large apparent Poisson ratio of the networks is associated with a decrease in sample volume during deformation. (H) The stretch energy of fibers normalized by the total strain energy as a function of the applied stretch. The curves in E and F correspond to results from the coarse-grained constitutive model (Eq. 1).

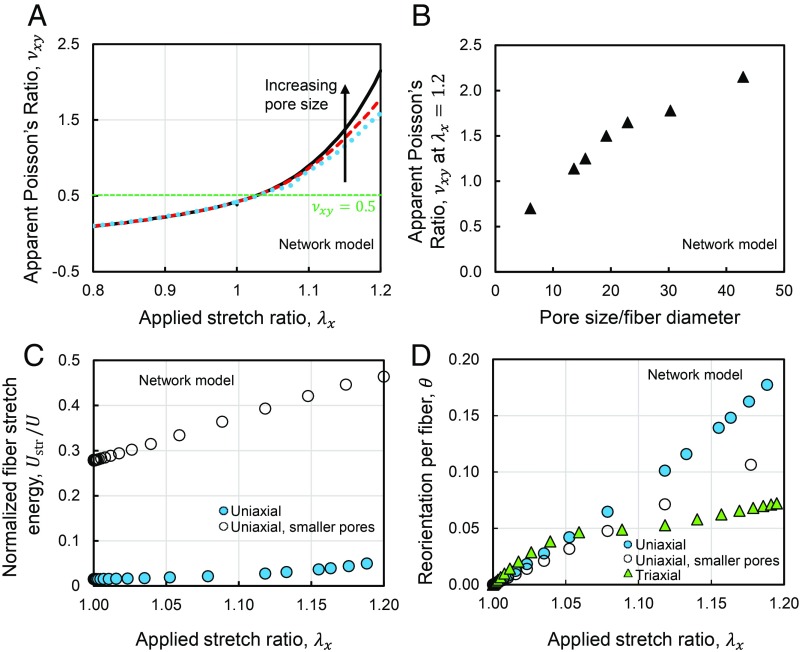
Next, we studied the effect of network pore size on the apparent Poisson ratio. We tested networks with different pore sizes by changing the number of random seeds used to generate the Voronoi fiber networks. Tests using networks with smaller pores demonstrated that the apparent Poisson ratio increases with increasing network pore size (Fig. 2 A and B). In networks with larger pores, the free segments of the fibers are longer. Because longer fibers buckle at smaller forces (35), the observed increase in the apparent Poisson ratio was caused by more frequent buckling of fibers in the transverse direction. The decreased apparent Poisson ratio in networks with smaller pores was also accompanied by a decreased share of fiber bending energy compared with stretching energy (Fig. 2_C_). The original network and the tested network with smaller pores (Fig. 2 C and D) correspond to ratios of pore size/fiber diameter of 43 and 23, respectively. In equibiaxial stretch deformation, the network was simultaneously stretched in the x and y directions, while it was free to contract in the transverse direction. The biaxially stretched networks exhibited a much larger transverse contraction compared with the uniaxially stretched networks. This behavior was accompanied by a stiffer response and an earlier transition to strain–stiffening (Fig. 1_E_), signified by a smaller threshold stretch at which stiffening became significant. The threshold stretch was even smaller when the network was subjected to triaxial expansion, and the network exhibited less fiber reorientation in triaxial tests than in uniaxial and biaxial tests (Fig. 2_D_). The degree of fiber reorientation was associated with straightening of individual fibers and groups of fibers, transmitting tensile forces. The straightening of fibers has also been previously observed in shear deformation of fiber networks (36). Despite the smaller fiber reorientation and the absence of fiber alignment, the network behavior was stiffer in triaxial expansion tests compared with the uniaxial case. The stiffer network response and the earlier transition to strain–stiffening were accompanied by higher levels of stretching of individual fibers compared with bending (Fig. 1_H_). As the long and thin collagen fibers are much stiffer in stretching compared with bending, the stretch-dominated network response in triaxial deformation causes a stiffer behavior compared with the response observed in the uniaxial tests.

Fig. 2.

Fig. 2.

The role of fiber reorientation and fiber stretching in the pore size-dependent multiaxial coupling and Poisson effect of fibrous networks. (A) The apparent Poisson ratio of fiber networks versus uniaxial stretch at different concentrations of collagen. The network pore size was tuned by changing the number of random seed points used to generate the network geometry. (B) Apparent Poisson’s ratio of the networks at a stretch of 1.2 for networks having different pore sizes. (C) The normalized fiber stretch energy is larger in networks with smaller pores subjected to uniaxial stretch. (D) The reorientation per fiber as a function of the applied stretch in uniaxial and triaxial deformation and uniaxial deformation of a network with smaller pores. The reorientation of each fiber was calculated as the angle between the vectors marking the orientation of the fiber before and after deformation. In C and D, the original network and the network with smaller pores correspond to values of pore size/fiber diameter of 43 and 23, respectively.

Motivated by recent studies on the connectivity of collagen networks polymerized in different conditions, we used our network models to test the presence of the anomalous apparent Poisson ratios in networks with various network connectivities. Previous measurements reported a value of 3.4 for the mean nodal coordination number of collagen networks, 〈z〉 (the average number of fiber segments attached at a junction) (37). Moreover, 〈z〉 varies with the conditions of network polymerization, such as temperature, pH, and ionic concentrations (14). We used our 3D Voronoi network model and a 3D lattice-based network model (SI Appendix) to test the Poisson effect in networks with 〈z〉 values close to parameters for networks polymerized at 37 °C and various collagen concentrations. The parameter 〈z〉 was changed by randomly detaching a pair of fiber segments from a shared junction, following a procedure similar to the common approach in the studies on network connectivity (14, 38). These tests demonstrated the presence of an anomalous apparent Poisson ratio larger than 0.5 in the networks having a range of 〈z〉 values (SI Appendix, Fig. S3). The connectivity of the lattice-based network was also changed by varying the mean number of lattice spacings per straight fibers, L/lc. Networks having a range of L/lc also exhibited apparent Poisson’s ratios larger than 0.5 (SI Appendix, Fig. S3_C_). The L/lc and 〈z〉 values were tuned to reproduce the recent values reported on collagen networks (14) as well as a network with hypothetically high connectivity. The network with hypothetically high connectivity had 〈z〉=4, which is still below the isostatic limit of 6 in 3D networks (39–41).

Taken together, our network model demonstrated the dependence of anomalous multiaxial stiffening and Poisson effect in fiber networks on pore size and network connectivity. In uniaxial tension, external loading causes fiber rotation and buckling in the transverse direction, whereas simultaneous stretching of the network in the other directions prevents the reorientation and buckling of fibers in the transverse directions. In this state, the fibers are forced to stretch to accommodate the externally applied strains, causing a stiffer response due to the higher stiffness of fiber stretching compared with bending. Therefore, the biaxial and triaxial stretch tests were accompanied by earlier transitions to strain–stiffening and higher magnitudes of stiffening compared with the uniaxial tests.

The Anomalous Ratio of the Biaxial to Uniaxial Stiffness of the Networks Increases with Increasing Network Pore Size.

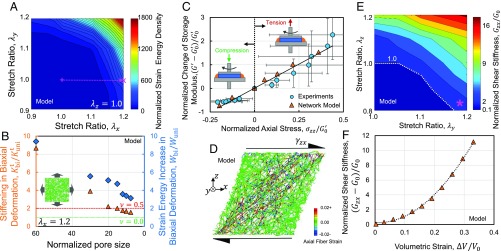
Next, we tested networks stretched by λx and λy in the x and y directions, respectively (SI Appendix, Fig. S1_E_). Stretch values ranging from 0.9 (compression) to 1.2 (tension) were applied along each axis. We characterized the network deformation by measuring the strain energy per unit volume of the material in the undeformed state, W. The results indicate the presence of stronger strain–stiffening when the two axes were simultaneously subjected to stretch. The stiffening effects persisted if at least one of the applied stretches was larger than the threshold of strain–stiffening (Fig. 3_A_). We also measured the change of the tangent stiffness (ratio of the instantaneous changes in stress and stretch), Kt, and strain energy density of the equibiaxially stretched networks as a function of network pore size. Surprisingly, the ratio of the biaxial to uniaxial stiffness was about 8. This ratio is much larger than the maximum value of 2 for linear isotropic materials. The relative stiffening, Kbit/Kunit, and increase in strain energy, Wbi/Wuni, decreased with decreasing network pore size (Fig. 3_B_), demonstrating a trend similar to the apparent Poisson ratio (Fig. 2_B_).

Fig. 3.

Fig. 3.

The pore size-dependent stiffening of fibrous networks in triaxial and biaxial deformation. (A) Map of the normalized strain energy density of a fiber network in biaxial stretch tests. (B) Stiffening of networks in equibiaxial deformation increases with increasing network pore size. The stiffening in biaxial deformation and strain energy increase in biaxial deformation are displayed using red triangles and blue diamonds, respectively. In these tests, pore size was tuned by changing the number of random seed points used to generate the network geometry. The reported pore size was normalized by the fiber diameter. The maximum possible biaxial-to-uniaxial stiffness ratio for linear elastic isotropic materials corresponds to materials having ν = 0.5 (red dashed line). The biaxial and uniaxial stiffnesses are equal for linear elastic isotropic materials exhibiting no Poisson effect, ν = 0.0 (green dotted line). The Inset displays a snapshot of a fiber network tested in equibiaxial tension. The horizontal axis is plotted in reverse. (C) Variation of network storage modulus against axial stress. Two different samples were used in the tension and compression rheological experiments. The Insets display schematics of the coupled axial–shear rheometry experiments in tension and compression. A _G_′0 value of 450 Pa was used in normalizing the rheological data. (D) Snapshot of a fiber network model in shear loading after multiaxial deformation. Colors display the axial strain of fibers. (E) The map of the network shear modulus after biaxial deformation indicates that the networks become stiffer in shear if at least one of the applied axial stretches is larger than the strain–stiffening threshold. The purple asterisk marks the increase in shear modulus of a network under compression in one direction and tension past the stiffening threshold in another direction. (F) The apparent shear stiffness of a fiber network increases with volumetric expansion. The dashed curve is plotted to guide the eye. All panels present results obtained using the computational fiber network model, and C also includes results from the axial–shear rheometry experiments.

Effect of Shear: The Storage Shear Moduli of Collagen Networks Change in Proportion to Applied Axial Stresses.

To further study the coupling of the deformation modes, we assessed the influence of axial deformation on the shear response of the collagen networks in rheometry experiments. We performed small-strain oscillatory shear tests on stretched and compressed samples. We repeated these tests at various amounts of stretch and compression, measuring the shear storage modulus, G′, and applied axial stress. The network G′ increases and decreases linearly with increasing axial tensile and compressive stress, respectively (Fig. 3_C_). The increase of G′ with increasing axial stress is larger in tension compared with its decrease in compression. We obtained similar results in combined axial and shear tests of thin fiber network models (Fig. 3_C_). This result is consistent with previous experimental and theoretical reports of the increase of G′ with increasing tensile stress and decreasing G′ with increasing compressive stress in collagen and fibrin networks (23, 42, 43).

Effect of Shear: The Shear Modulus of the Networks Increases with Biaxial and Volumetric Expansion.

Next, we investigated the influence of shear deformation on the networks that are initially deformed in biaxial and triaxial tests using the network model (Fig. 3_D_). In the biaxial–shear case, we conducted tests that reproduce the loading conditions similar to those experienced by the collagen-rich capsular ligaments of the spine (44, 45). We stretched the networks by λy and λz in the y and z directions, respectively, and then subjected them to shear loading by moving the top and bottom surfaces of the network in opposite directions along the x axis. The network was stiffer in shear if it was stretched beyond the stiffening threshold in at least one of the axial stretch directions (Fig. 3_E_). In particular, the shear stiffness increases even if the smaller stretch ratio corresponds to compression.

When the network was uniaxially stretched past the stiffening threshold, a group of fibers reoriented and aligned toward the direction of tension, whereas another group buckled in the transverse direction. Subsequent compression of the network transverse to the stretch direction caused more buckling of fibers in that direction. At this state, if the network was sheared, deformation of the network required reorientation and stretching of the fibers that were aligned as tension was applied. The stiff response of the aligned and stretched fibers dominates the network’s shear response, and therefore the network’s shear stiffness is larger than the shear modulus of the undeformed network.

Finally, we studied the combination of shear deformation and triaxial expansion. In this case, we applied deformations that reproduce the loading conditions mimicking the shear deformation of swollen tissues, such as those occurring in the rheological testing of osmotically swollen gels. We simultaneously stretched the network in all three directions and then displaced the top and bottom faces in opposite directions along the x axis. Shear deformation was accompanied by the stretching of fibers oriented diagonally, along the maximum principal stretch direction (Fig. 3_D_). During shear, in the absence of volumetric expansion, stretching of groups of fibers was accompanied by bending and reorientation of fibers. In contrast, after volumetric expansion, the groups of fibers, which coincided with the maximum principal stretch direction in shear, were already straightened. Subsequent shear deformation of the network was, therefore, accompanied by large stretching of fibers. Since the fibers are much stiffer in tension than in bending, the network shear stiffness increased with increasing volumetric strain (Fig. 3_F_).

A Coarse-Grained Constitutive Model for Multiaxial Coupling and Poisson Effect of Collagen Networks.

To efficiently model the multiaxial effects at large-scale fibrous matrices, we used insights from our microstructural fiber network model and developed a coarse-grained constitutive model. The present model has the same spirit as our previous constitutive model (26) of the long-range transmission of cellular forces in fibrous matrices (16). Notably, the present model also accounts for the coupling between the different modes of deformation and the Poisson effect. Here, the mechanical response of the fibrous matrices is represented by a strain energy density function:

W=Wb(I¯1,J)+∑i=13f(λi)+g(∑i=13∑j≠iζij). [1]

The terms that include Wb and f were introduced in our previous model (26), whereas the term including g is added here to account for the coupling of the multiaxial deformations and the Poisson effect. Wb represents the strain energy of the fibers, which are not reoriented toward the loading direction. Wb follows a neo-Hookean form:

Wb(I¯1,J)=μ02(I¯1−3.0)+κ2(J−1.0)2, [2]

where μ0 and κ define the stiffness of the unaligned fibers in the shear and volumetric modes of deformation, respectively. I¯1 is the trace of the isochoric right Cauchy–Green deformation tensor, and J is the matrix volume normalized by the volume in the undeformed configuration. The function f represents the strain–stiffening response of the aligned fibers in each of the principal directions. The second derivative of f with respect to the principal stretches is related to the stiffness of the network as follows:

∂2f(λi)∂λi2={μ,λi≤1.0μexp(mf(λi2−1.0)),λi>1.0. [3]

The stiffness is μ in compression, whereas strain–stiffening is present in tension and follows an exponential trend. mf is the exponent that controls the magnitude of strain–stiffening in uniaxial tension. The exponential response mimics the constitutive laws previously proposed by Fung to model the stretch of collagen-rich soft tissues (46, 47), and the strain–stiffening response of certain reconstituted collagen networks (13).

To model the coupling of the deformation modes in the different principal axes, the principal stretches, λi, are combined, and six parameters ζij are defined as follows:

Here, α is a parameter that governs the strength of the coupling of the principal axial modes (SI Appendix). The sum of the six ζij parameters, t, is input to the function g, defined using a piecewise expression similar to f,

∂2g(t)∂t2={0,t≤6.0μexp(mg(t−6.0)),t>6.0. [5]

Before deformation, the principal stretches equal 1.0, the ζ parameters are 1.0, and, therefore, t=6.0. g grows exponentially with triaxial stretching, where t>6.0, and vanishes in triaxial compression, where t<6.0. The exponent mg tunes the magnitude of multiaxial coupling in the strain–stiffening regime. We implemented the coarse-grained constitutive model as a user-defined material in the finite element package COMSOL 5.3 (Comsol Multiphysics) (48).

We tested the coarse-grained model in uniaxial, biaxial, and triaxial tests using procedures similar to those used in the case of the network model. The parameters of the coarse-grained model were calibrated by comparing the resulting stress–strain curves and the stretch ratios transverse to the loading direction with the results from our fiber network model (Table 1). The resulting stress–strain curves (Fig. 1_E_) and the transverse stretch ratios (Fig. 1_F_) obtained using this model agree with the results obtained using the microstructural fiber network model. The magnitude of the Poisson effect can be tuned by changing the parameter α (SI Appendix, Fig. S4).

Table 1.

The parameters used in the coarse-grained constitutive model

Parameter Value
μ 1.00 (kPa)
μ0 0.03 (kPa)
κ 1.67 (kPa)
mf 5.00
mg 0.01
α 10

Poisson Effect Leads to a 100-Fold Increase in the Perceived Stiffness of Thin Collagen Gels in Extensional Rheology.

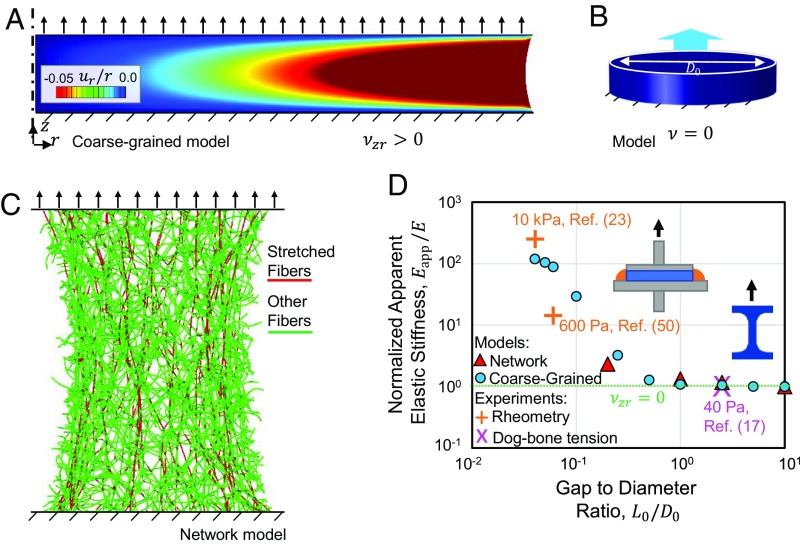
We apply our computational coarse-grained model to study the geometry dependence of the multiaxial coupling of the networks. The model predicts a stiffer response as thin collagen gels are stretched while they are not free to contract in the transverse directions. Our computational model comprised short disk-shaped samples of diameter D0 and height L0 subjected to uniaxial tension. The top and bottom faces of the disks were stretched in the vertical direction, z, while they were fixed in the radial direction, r (Fig. 4_A_). Tests using the computational coarse-grained model demonstrated that the lateral free surface of the stretched gel curves inward (Fig. 4_A_). Preventing the transverse contractions of the network hinders its contraction by the Poisson effect. The computationally observed curving is accompanied by a highly inhomogeneous strain field (Fig. 4_A_). The elastic stiffness measured in these tests was orders of magnitude larger than the initial elastic modulus computationally obtained in the uniaxial tests of longer samples, where the samples are less constrained to contract in the transverse directions.

Fig. 4.

Fig. 4.

Influence of the Poisson effect on the apparent stiffness of thin collagen networks in extensional rheology tests. (A) The response of the computational coarse-grained constitutive model in the instantaneous extension of a thin sample. The sample curves inward at the free boundary due to the positive apparent Poisson ratio. The axis of symmetry is marked by a vertical dashed-dotted line. (B) Computational models of isotropic linear elastic materials do not exhibit curving or inhomogeneity of strain in the absence of the Poisson effect, for ν = 0.0. The dark blue color indicates vanishing radial strain in the sample. The color scale of A is also used in plotting the snapshot in B. (C) Snapshot of a computational fiber network model in tension. (D) The ratio of apparent elastic stiffness over the elastic modulus of the gels as a function of the specimen length (or thickness)-to-diameter ratio. The experimental data points were collected from rheometry experiments (23, 50) and tension experiments using dog bone-shaped samples (17). In addition to experiments, results are plotted from the computational network model and the computational coarse-grained model. Both axes are plotted logarithmically. The Insets display gels tested using (Left) extensional rheometry and (Right) uniaxial stretch of dog bone-shaped samples.

When we repeated the computational stretch tests, using isotropic linear elastic samples with vanishing Poisson’s ratios, we did not observe curving at the free lateral surfaces (Fig. 4_B_), and the elastic stiffness was equal to the material’s elastic modulus, corresponding to stiffness in the uniaxial tests of long samples. This result signifies the relation between the Poisson effect and the increased apparent stiffening of thin samples. Repeating the stretch tests using the computational fiber network model demonstrated a stiffened response with inward curving of the sample close to the free lateral surface (Fig. 4_C_). The apparent elastic stiffness, in this case, was also higher than the elastic modulus, observed in the uniaxial tests. We observed fiber reorientation and highly stretched fibers, which formed paths connecting the top and bottom surfaces, whereas aligned fiber bundles were absent (Fig. 4_C_).

To measure the apparent elastic stiffness of samples having various aspect ratios, we performed calculations using both the computational network model and the computational coarse-grained model. We computationally tested samples of length-to-diameter ratios ranging from 0.05 to 10. The apparent elastic stiffness was calculated as the ratio of the normal component of the surface traction over the top sample surface to the applied strain in the vertical direction. As we decreased the sample length (or thickness)-to-diameter ratio, L0/D0, by about two decades, the apparent stiffness of the sample increased by about 10 times (Fig. 4_D_).

The reported stiffening effect computationally observed during the extension of thin reconstituted collagen samples was verified by comparison with the experimental results collected from the literature (Fig. 4_D_). We ensured that in all experiments, collagen type I was used, and the conditions of network polymerization, such as temperature and pH, were similar, and treatment with pepsin during collagen purification, which greatly decreases the stiffness of collagen gels (49), was not used in any the experiments. SI Appendix, Table S1 summarizes the conditions under which the collagen networks were polymerized in the different cited experiments. The experimental elastic stiffness values were obtained by evaluating the slope of the line fitted to the stress–strain curves of stretched collagen gels at 3% strain. The 40-Pa data point corresponds to uniaxial stretch tests conducted using long dog bone-shaped samples (15). In this case, the sample shape differed from the other cylindrical samples, and the sample aspect ratio provides a rough estimation for comparisons. We calculated the 600-Pa and 10-kPa values using the stress–strain results of extensional rheology tests performed at various sample gap and diameter sizes (23, 50). This result confirms the orders of magnitude of increase in the apparent elastic stiffness of short samples.

By considering the linear elasticity of the isotropic networks at small strains, we expect the shear modulus, G, and the elastic modulus, E, to be related as G=E/(2(1+ν)), where ν is the small-strain Poisson ratio. The extensional rheology tests, however, report values measured in kilopascals (23, 50), whereas the values obtained using shear rheology tests of similar networks are measured in pascals (13). Our model relates these seemingly disparate values by accounting for the stiffening by the sample thinness in extensional rheology tests. The thickness effect dominates the changes in stiffness, although some of the tests were performed using slightly different methods and cross-sectional sample shapes. Our calculation results in elastic moduli from extensional rheology tests that are consistent with the shear moduli measured using shear rheology experiments (13), relating the seemingly disparate values previously reported in extensional and shear rheology experiments.

The Poisson Effect Facilitates Higher Fiber Densification Induced by Cellular Contractility in Less Dense ECMs.

To test the effect of network density on the Poisson effect and assess its role in ECM mechanics in the tumor microenvironment, we conducted cell–ECM experiments using transformed mammary epithelial cells and collagen type I gels. We prepared mammary acini, seeded them atop collagen gels, and using particle image velocimetry (described in Materials and Methods) measured the strain fields over the collagen networks induced by the contractile cell clusters.

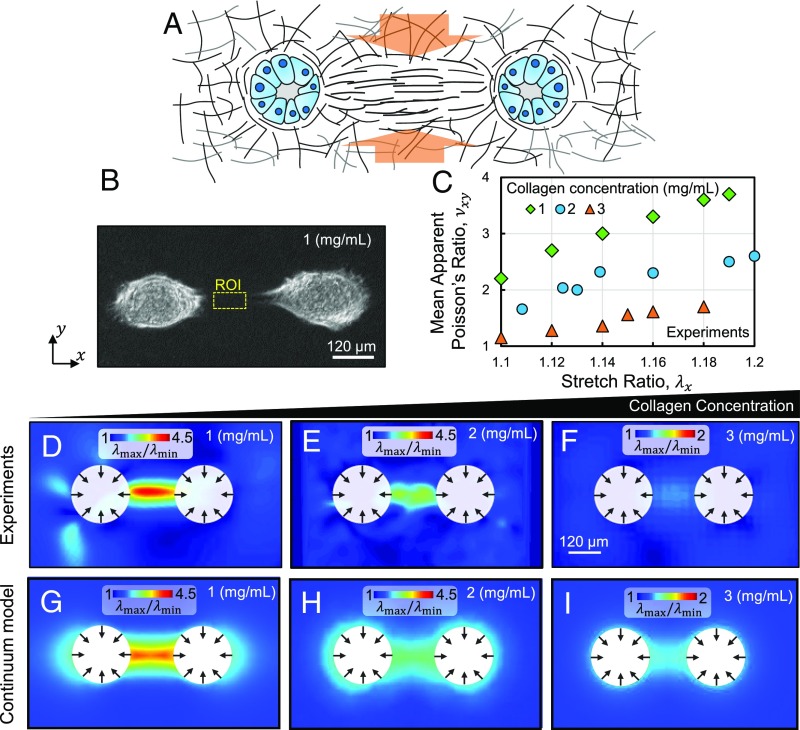
Ten hours after seeding, tensile stretches developed in the matrix along the lines connecting nearby pairs of cell clusters. The tensile stretches were accompanied by contractions in the transverse direction. Fig. 5 A and B displays a schematic of the transverse stretch ratio and bright-field image of a pair of interacting acini. The resulting strain field exhibits a large ratio of the maximum to minimum principal stretches at the line connecting the nearby acini, signifying large Poisson effects. We evaluated the mean axial stretch ratio and apparent Poisson ratio over a region of interest (ROI) selected along the line connecting the nearby acini (Fig. 5_B_, yellow dashed lines). Our calculations demonstrated that, in agreement with the observations from our network model, the mean apparent Poisson ratio in the ROI increases with increasing mean stretch ratio (Fig. 5_C_). Also, in agreement with results from our network model, the apparent Poisson ratio was larger than 1.

Fig. 5.

Fig. 5.

The density-dependent Poisson effect in collagen ECMs induced by cellular forces. (A) Schematic of the Poisson effect in a collagen tract formed by a pair of mechanically interacting cell clusters. The studied fibrous tracts promote the invasion of cancerous acinar cells. (B) Bright-field image of a pair of interacting acini, showing the two cell clusters atop a gel formed at a collagen concentration of 1 mg/mL. The region of interest (ROI) is marked by the yellow dotted box. (C) Mean apparent Poisson’s ratio at the ROI as a function of stretch in the horizontal direction. (D_–_F) The ratio of the largest to smallest principal stretch ratios in collagen gels deformed by a pair of mammary acini. Collagen gels polymerized at collagen concentrations of (D) 1, (E) 2, and (F) 3 mg/mL were tested. (G_–_I) The corresponding results obtained using the coarse-grained model. D_–_I correspond to a mean _λ_max = 1.1 at the ROI. All panels except C correspond to a pair of cell clusters, seeded atop the horizontal surface of a gel, as viewed from the top.

Next, we assessed the density dependence of the Poisson effect by polymerizing gels at collagen concentrations of 1, 2, and 3 mg/mL. The transverse contractions of the denser networks were smaller at the same axial stretch ratios, signified by a smaller ratio of the principal stretches (Fig. 5 D_–_F). The orientations corresponding to the maximum and minimum principal stretches are parallel and perpendicular to the orientation of the fibrous tracts (SI Appendix, Fig. S5 B and C). The mean apparent Poisson ratio was also smaller in the gels formed at a higher collagen concentration (Fig. 5_C_). The larger Poisson ratio of the less dense networks facilitates the densification of fibers at the collagen tracts, associated with the invasion of the cancerous acinar cells.

We qualitatively compared the experimentally observed increase of the apparent Poisson ratio with decreasing collagen concentration with the variation of the apparent Poisson ratio observed in network models as a function of the various microstructural parameters. Gels formed at 37 °C and pH values between 7.0 and 7.5 were considered here, and variations of these parameters were not investigated. We begin by recalling the previous experimental reports of the variation of network parameters in collagen gels formed at various concentrations. First, we note that a recent study reported the average nodal coordination number, 〈z〉, values of 2.91, 3.07, 3.05, 3.10, and 3.18 for gels formed at collagen concentrations of 1, 2, 3, 4, and 5 mg/mL polymerized at 37 °C (14). Second, previous experiments consistently indicated an inverse relationship between the square of pore size and polymer concentration in collagen gels (13, 51, 52), signifying that with decreasing collagen concentration, the pore size increases. Finally, previous experiments using confocal reflectance and fluorescence microscopy (52), turbidimetry (14), and a combination of second harmonic generation imaging microscopy and transmission electron microscopy (53) indicated that, with decreasing collagen concentration from 3 to 1 mg/mL, fiber diameter either decreases or changes insignificantly. [We note that experiments using dried fibers imaged using scanning electron microscopy reported increasing fiber diameter with decreasing collagen concentration (3). Here, we did not consider the measurements using dried fibers as the studied networks were submerged in all cases. In the network models, at the same applied strain, the diameters of the fibers, rather than their Young’s moduli, are important in determining the apparent Poisson ratio.] These results indicate a larger dimensionless ratio of pore size to fiber diameter in the gels formed at a lower concentration. The results of our network models indicate increases of apparent Poisson’s ratio with increases in the ratio of pore size to fiber diameter (Fig. 2_B_), and either unchanged or increasing apparent Poisson’s ratio with decreasing network connectivity (SI Appendix, Fig. S3). The results of our experiments, therefore, qualitatively agree with the trends predicted by our network models.

We reproduced the density-dependent Poisson effect induced by cell contractility using our coarse-grained model (Fig. 5 G_–_I). In these figures, cellular contractility of a cell cluster was modeled by an isotropic distribution of displacements over the perimeter of a circle. The effects of anisotropic distributions of displacement are discussed in SI Appendix (SI Appendix, Fig. S6). The 1, 2, and 3 mg/mL networks were modeled using α values of 12, 10, and 8, and the finite-element simulations were performed using 3D tetrahedral elements.

Conclusions and Outlook

Multiaxial coupling of deformation modes and the underlying Poisson effect characterize important aspects of the mechanical response of collagen networks and demonstrate synergistic stiffening of the fiber networks in multiaxial loading. These results point to a counterintuitive effect: When a network is stretched in one direction, despite the buckling of fibers in the transverse directions, the network becomes stiffer in the transverse direction. In fact, stress drastically increased as we stretched the fiber networks in the transverse direction following uniaxial tension. The magenta markers in Fig. 3_A_ show that the contour curves of strain energy are closer in the vertical direction in a uniaxially stretched network (cross sign) in comparison with the networks before deformation (plus sign). The reported effect is distinguished from the behavior of an incompressible material partly because the networks shrink in volume when subjected to uniaxial tension. Similar large changes in volume, accompanied by the expulsion of water/interstitial fluid, have also been previously reported in stretch tests of collagen-rich tissues such as tendons (54, 55). The deformation of the networks is distinguished from materials with a Poisson ratio of 0.5 also by their higher biaxial-to-uniaxial stiffness ratio (Fig. 3_B_).

Poroelastic effects should also be considered in analyzing the mechanics of collagen gels and collagen-rich tissues since they include a large concentration of interstitial fluid. In a gel stretched by 20% strain in the x direction, the relative volume of the gel, J, is related to the apparent Poisson ratio as J=1.2(1−νxy/5)2. This relationship indicates a drastic reduction in the volume of the gels, associated with the observation of the anomalously large apparent Poisson ratios (Fig. 5_C_). In soft gels, it is commonly assumed that the individual polymers and water molecules are incompressible and that there is negligible void space in the gel (56). Consequently, the change in the volume of the gel during mechanical loading is entirely due to the volume of the absorbed/expelled fluid. This condition of molecular incompressibility allows us to express the change in the concentration of the fluid, ΔC, in terms of the change in the volume of the gel as 1+vΔC=J, where v is the volume per water molecule. Compared with uniaxial deformation conditions, a larger fluid pressure is expected in biaxial deformation due to the larger Poisson effect in latter case. The mechanical response of the fluid-filled networks consists of two components associated with network deformation and the fluid pressure. We expect that, with time, stresses relax as water is expelled from the gel, and that the water pressure should decrease. At higher concentration of collagen, smaller network pore sizes (51, 52) lead to decreased permeability of water (57, 58), and consequently a more gradual relaxation response is expected. Our network model also showed an anisotropic evolution of the size of pores in uniaxial and biaxial loading, implying anisotropic permeability of the networks. Studying the time-dependent multiaxial behavior of water-filled networks of various collagen concentrations can be an interesting topic for future studies.

The network pore size changes during network deformation because fibers reorient, stretch, and buckle. The pores become smaller in compression tests. Similarly, in the biaxial stretch tests, the substantial transverse contraction causes compaction of the fibers in the plane of stretching and hence reduces pore size. In the cases where pore size decreases, we expect the formation of new adhesions between fibers that come in contact (59). The newly formed adhesions prevent the elastic recovery of the network deformation, leading to residual deformation after the external forces are removed. In triaxial stretching, however, the network model exhibits no significant decrease in pore size. We, therefore, do not expect the occurrence of viscoplastic effects (27) due to the formation of new adhesions during triaxial swelling of collagen networks. Additionally, the movement of interstitial fluid has been previously suggested as a mechanism of transport in tissues (34, 60). Changes in pore size are expected to influence the patterns of the flow of nutrients and cytokines following matrix deformation (61), giving rise to a chemomechanical coupling in the response of ECMs with the deformation induced by cellular forces. Finally, although our model does not account for the failure of fibers or cross-links, based on the current results, we expect the networks to fail at smaller stretches in triaxial deformation than in biaxial and uniaxial stretch tests because both fibers and cross-links transmit larger stresses in triaxial stretch tests.

Our coarse-grained model was motivated by the fact that the existing continuum models of ECM mechanics do not account for the strong coupling between the axial modes of deformation and the Poisson effect observed in fibrous ECMs accompanied by apparent Poisson’s ratios larger than 1. By accounting for the triaxial coupling and the Poisson effect in collagen networks, our coarse-grained model provides a more accurate method for simulating ECM mechanics. Models of ECM mechanics can aid in the engineering of tissues, for instance by designing engineered tissue folding strategies (62). Such models are also employed in the simulations of the progression of diseases such as cancer (29, 30) and fibrosis. In the long term, computational modeling may help in patient-specific disease diagnosis and prognosis as well as in narrowing the space of possible treatment options.

Materials and Methods

Microstructural Voronoi Fiber Network Model.

Fiber networks were generated using 3D Voronoi tesselations. The initial network geometry was created by placing fibers over the edges of a 3D Voronoi diagram with random seed points. The pore size of the 3D networks was tuned by changing the number of the seed points. Networks had average nodal coordination of 3.2, unless stated otherwise. In the tests with varying network connectivity, the average nodal coordination number of the network was tuned by randomly detaching fibers from junctions shared by multiple fibers. Fiber waviness was then induced by shaping individual filaments into half-sine waves. Individual fibers were modeled as elastic Timoshenko beams that are flexible in stretching, bending, twisting, and transverse shear. The fibers have circular cross-sections of diameter 150 nm and elastic moduli of 6.5 MPa. Implicit finite element modeling was performed using the finite element package Abaqus (Simulia) (63). In triaxial tests, external loading was performed by prescribing the displacements of the nodes located on the sample boundaries, whereas in biaxial and uniaxial tests, the lateral sample surfaces were traction free. All calculations were performed using displacement-controlled boundary conditions.

Rheometry.

Collagen type I gels were prepared using collagen isolated from calf skin (MP Biomedicals), dissolved in 0.005 M acetic acid. 10× PBS, 0.1 M NaOH, and ddH2O were warmed to room temperature and added in appropriate ratios to yield a 3 mg/mL collagen concentration in 1× PBS solution with pH between 7 and 7.5. The gels were polymerized at 37 °C. The gels were tested using a Kinexus rheometer (Malvern). Parallel plates of diameters and gap of 25 mm and 1 mm were used. The bottom plate incorporated a Peltier element, allowing temperature control at 37 °C. The samples were pipetted between the plates before polymerization. After polymerization, the appropriate buffer was pipetted around the free edge of the sample to prevent drying and allow free fluid flow in and out of the samples. The shear moduli of the samples were measured by applying a small oscillatory shear strain of 2% at a frequency of 10 rad/s. Axial strain was applied by changing the gap between the plates. The samples were subjected to a fixed step compression or extension, after which a shear test was performed. During the axial strain series, the samples were allowed to relax between 100 and 1,200 s before continuing to the next level of axial strain.

Collagen Tract Formation by Cellular Contractility.

Rat tail collagen (Corning) was gelled at concentrations of 1, 2, and 3 mg/mL on prechilled glass-bottom imaging dishes (MatTek) according to the manufacturer’s protocol. Briefly, solubilized collagen was diluted using 10× Tris-buffered saline and 5 (mM) NaOH; 300 (μL) was plated on the 20 (mm) glass-bottom portion of a 35 (mm) dish (MatTek). For measuring substrate displacement, 1-μm Nile Red (535/575) fluorescent beads (Life Technologies) were added at 2,000× dilution from a 2% (wt/vol) stock. Dishes were incubated at 37 °C for 30 min. MCF10AT acini were cultured and extracted as previously described (9, 64). Collagen gels were rinsed with MCF10A media, and the acini were seeded on the gel portion of the dish. The dishes were incubated at 37 °C for 2 h to allow the acini to settle before adding more media, collagen staining, and live imaging. Collagen was stained by purified CNA35-SNAP.

In-plane gel deformation was measured by projecting a 30-μm-thick volume centered at the surface of the gel and using particle image velocimetry (65), generating displacement vector fields, u (SI Appendix, Fig. S5). For a material particle moving from initial position X to final position x, displacement, u, was evaluated as x−X. The displacement field was then used to numerically calculate the deformation gradient tensor F=∇Xx, in index notation: Fij=∂xi/∂Xj. The deformation gradient was then used to calculate the stretch tensor as U=(FTF)1/2. The principal stretches, λmax and λmin, are the eigenvalues of U and correspond to the orientations along the directions of the eigenvectors of U (66).

Supplementary Material

Supplementary File

Acknowledgments

This work was supported by National Cancer Institute Awards U01CA202177 (to V.B.S.) and U54CA193417 (to V.B.S. and P.A.J.); National Institute of Biomedical Imaging and Bioengineering Award R01EB017753 (to V.B.S.); NSF Center for Engineering Mechanobiology Grant CMMI-154857); and NSF Grant MRSEC/DMR-1720530.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File