Cell migration and organization in the intestinal crypt using a lattice‐free model (original) (raw)
Abstract.
We present a novel class of spatial models of cell movement and arrangement applied to the two‐dimensional cellular organization of the intestinal crypt. The model differs from earlier approaches in using a dynamic movement on a lattice‐free cylindrical surface. Cell movement is a consequence of mitotic activity. Cells interact by viscoelastic forces. Voronoi tessellation permits simulations of individual cell boundaries. Simulations can be compared with experimental data obtained from cell scoring in sections. Simulation studies show that the model is consistent with the experimental results for the spatial distribution of labelling indices, mitotic indices and other observed phenomena using a fixed number of stem cells and a fixed number of transit cell divisions.
Introduction
The small intestinal tract is lined by a polarized mono‐layer epithelium, which is folded into crypts and villi. The crypts in the small intestine of mice contain about 235–250 cells (Potten et al. 1988), of which about 150 are rapidly proliferating with a cell cycle time of approximately 12 h. Proliferation is restricted to the lower two‐thirds of the crypt. Cell differentiation and function take place primarily in the upper parts of the crypts and on the villi (1975, 1979; Potten et al. 1997).
The present concept of cellular organization implies a cell lineage with a small number of long‐lived self‐regenerating stem cells located near the bottom of the crypt giving rise to transit cells with a limited and decreasing capability of further amplifying cell divisions (Loeffler & Potten 1997).
To resolve the question whether such a pedigree is consistent with the spatial ordering in the intestinal crypt, several modelling studies have been undertaken. The first comprehensive model analysis of the 2‐D cell layer in the murine crypt was introduced in Loeffler et al. (1986) and similar models were independently discussed in Finney et al. (1989), Meinzer et al. (1992), Paulus et al. (1993) and Isele & Meinzer (1998). These models were based on a 2‐D rigid lattice with rectangular cell layouts and included assumptions about the number and spatial positions of stem cells, the number of transit cell divisions, cycle times and migratory properties of daughter cells.
These lattice‐based dynamic models could explain a large amount of experimental data for the steady‐state situation such as positional changes in mitotic and thymidine labelling indices with space and time. However, to satisfy the requirement of a sharp confinement of proliferative cells to the lower half of the crypts and an appropriate mixture of labelled and unlabelled cells in adjacent cell columns, the introduction of migration rules was required to achieve a local homogeneity with regard to cell lineage age (Loeffler et al. 1986). One such hypothetical mechanism involved a cell–cell interaction leading to a local age‐dependent displacement of newborn cells. It was suggested that all cells have a certain ability to sense the age of their direct neighbours and preferentially divide in such a way as to shift their oldest neighbours. Such a process would yield a local age homogeneity by successfully displacing old cells to higher cell positions.
A later model refinement developed in our group (Paulus et al. 1993) was able to explain the differentiated Goblet cell distribution under the assumption that Goblet cells are offspring of specific transit cell generations.
All of these models, however, suffer from several conceptual problems. First, lattice‐based tissue models cannot account for the continuous growth and migration of individual cells as their movement is restricted to discrete spatial steps. Inserting cells within a filled lattice leads to instant, far‐reaching changes in cell arrangement. Entire cell columns must be displaced upwards to generate the free space needed for a newborn cell, requiring the disruption of all cell–cell contacts of the neighbouring cells. Deletion of cells, for example, to model apoptosis, causes similar long‐distance disruptions, when neighbouring cells fill the hole in the lattice. This is biologically implausible. Second, in these models cell movement and cell mitosis are directly coupled, in spite of the observation that migration can be observed even after complete mitotic arrest (Kaur & Potten 1986a). Third, the lattice‐based model crypts did not reflect the effect of the polygonal packing arrangements in crypts, but were designed so that lattice columns could be directly mapped to biological longitudinal sections. The lattice model thus directly mimicked the experimental artefact of 40% overscoring of cell positions within longitudinal sections (Potten et al. 1988).
In contrast, the model presented here was partly designed to mimic the experimental sectioning process appropriately and to control for the overscoring effect, which is due to the polygonal packing of the cells (Potten et al. 1988).
The main objective of our present study was to investigate whether a model based on a more realistic, mechanistic basis involving continuously moving cells on a 2‐D cylindrical surface conforms to the available data at steady state. We specifically examined the necessity of the local age sorting rule and the dependence of the pedigree concept on the lattice assumptions.
MATERIALS AND METHODS
Experimental data
In this paper we use as a reference data set the control data from an experiment published and explained in detail in Kaur & Potten (1986b). In brief, 16 male B6D2F1 mice received 25 µCi 3HTdR intraperitoneally at 9:00. Groups of four mice were killed at four different times (40 min, 3, 6 and 9 h). Samples of small intestine (ileum) were taken, fixed and processed for autoradiography. For each mouse, 25 clearly longitudinally sectioned crypts as identified by the presence of a lumen and Paneth cells at their bases were scored and at each cell nucleus the presence of label and mitotic figures was recorded.
From these 200 sections per time point the following statistics were produced: positional labelling indices (pLI), that is, the percentage of labelled cells at each cell position; positional mitotic indices (pMI), that is, the percentage of mitotic cells per position; run changes (Run), that is, the number of changes between labelled and unlabelled runs of cells within one section (Potten et al. 1982); and positional cell velocities (Qiu et al. 1994).
Model assumptions
The assumptions made about the pedigree concept and the cell kinetics closely follow those published by 1986, 1988, Potten & Loeffler (1987) and Paulus et al. (1993). We summarize the biological knowledge under heading (i) and describe our model assumptions under heading (ii). Heading (iii) gives technical and/or procedural remarks concerning this particular model implementation.
Crypt geometry
(i) The average crypt height is typically measured in numbers of cell nuclei seen in longitudinal sections (on average 21.9 cell nuclei per crypt side). On average 18.3 cell nuclei are counted per crypt circumference. A naive multiplication would suggest a crypt of about 400 cells. However, the intestinal mouse crypt contains only 235–250 cells, as measurements from unsquashed whole crypts showed. This discrepancy is due to the polygonal intercalated packing of cells, which results in experimental overscoring of cells not centred in the plane of sectioning (Potten et al. 1988) (see Fig. 1a,b).
Figure 1.
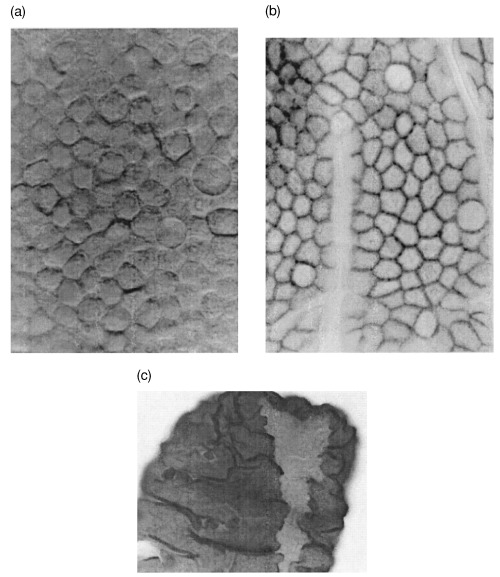
Intestinal villus. (a) Surface (differential interference microscopy); (b) β‐Catenin staining showing cell–cell borders (light microscopy); (c) NEU‐induced ribbon of mutated cells (light microscopy) (Loeffler et al. 1993).
The exact numbers and positions of active intestinal stem cells are unknown. Differentiated and non‐proliferative Paneth cells can be observed and counted easily. They typically form a cluster of cells at the bottom of the small intestinal crypt. The exact shape of this cluster differs from crypt to crypt, but the intracrypt amplitude between the lowest and highest Paneth cell position, measured from the lowest columnar cell, is not greater than 2 for about 90% of all crypts (Chwalinski & Potten 1989). The inter‐crypt amplitude is much larger, ranging from position 1 to 7 (see Table 1).
Table 1.
The average percentage of Paneth cells at each cell position. Experimental data from S. Chwalinski, as published in Loeffler et al. (1986)
| Crypt position | Model fit | Experiment |
|---|---|---|
| 1 | 99 | 75 |
| 2 | 88 | 71 |
| 3 | 71 | 68 |
| 4 | 54 | 60 |
| 5 | 38 | 45 |
| 6 | 21 | 21 |
| 7 | 5 | 5 |
| 8 | 0 | 0 |
(ii) The model crypt is considered as a cylinder. A cell i within the crypt is represented by a point (where ri is a vector to the centre and ri,j is a vector between two cells i and j) on a planar surface with cylindrical boundary conditions. This point is representative of the whole cell and can be interpreted as the centre of the nucleus. The tapered end of the crypt is assumed to be completely filled with kinetically inactive Paneth cells. The positions of the Paneth cells are randomly chosen at the bottom within a band (see i) of no more than two cell diameters. Stem cells are about equally distributed on top of the Paneth cells. The top of the crypt is the orifice to the villus.
(iii) A model crypt has Paneth cells only in positions 1 and 2. The inter‐crypt amplitude is modelled by adding zero to four layers of Paneth cells to the bottom end of the model crypt. Table 1 compares the resulting overall marginal Paneth cell distributions of the modelled crypts with experimental data.
For the crypt size, see (iii) below.
Cell shape and neighbourhood
(i) Seen in projection from the intestinal lumen, columnar cell boundaries have a convex polygonal shape of about equal area (Wright & Alison 1984, Vol. 2, p. 709). This can be seen very clearly on the villi with scanning light microscopy after β‐Catenin staining, as shown in Fig. 1b.
(ii) We assume that the polygonal shape of epithelial cells in the small intestine can be adequately described by a Voronoi diagram. For a given number of points, called generators, a Voronoi diagram describes boundary regions that include all points of the plane that are nearer to the corresponding generator point than to any other generator point. Voronoi diagrams are mathematically well defined and examined and have a number of properties that generally hold for biological cells. A measure of how well cell boundaries can be approximated by Voronoi diagrams was introduced by Honda (1978). This measure varies between different tissues, but Voronoi diagrams generally fit cell sheets with packed, polygonal‐shaped cells well, as exemplified in Honda (1978) for a piece of rat intestine. The individual shape of each cell results only from the location of the centre of the cell in relation to its neighbours. Cells are neighbours if and only if they share a common Voronoi polygon edge. This results in a variable shape of the boundaries and a variable number of neighbours for each individual cell. Epithelial cells are usually tightly linked to their neighbours by a complex of tight junctions and desmosomes (Browder et al. 1991, p. 328). Hence, adhesive forces counteract repelling forces due to volume exclusion.
We assume that all neighbouring cells tend to establish an equal distance from each other. Due to mitotic activity these distances change locally. Distances are not constant, but behave more like damped springs with a constant rest length s. An exception to this is newborn cells that reinsert into the plane after division. In this case, the spring rest length is dependent on the pair of new cells i, j and the time after division. This si ,j(t) value increases linearly from near zero to s within 1 h.
(iii) The graph that connects all neighbouring cell centres is a Delaunay triangulation. The Voronoi diagram, which is used to describe cell boundaries here, can be uniquely constructed from the Delaunay triangulation (Okabe et al. 2000). In our implementation we use as a triangulation algorithm the insertion method presented in Guibas & Stolfi (1985), which has an asymptotic complexity of n log n, where n is the number of generator points.
The Voronoi diagram used is defined on the surface of a cylinder (Okabe et al. 2000, p. 209) This ensures a finite size of the polygons along the circumference. Nevertheless, polygons at the top and bottom may be biased due to potentially unbounded polygons there. The unmoveable Paneth cells prevent this if near the bottom. To minimize infinite size effects at the crypt orifice we elongated the modelled crypt by one‐third beyond the assumed orifice (upper horizon).
The parameter s is set to 1/10 of the crypt circumference for all simulations.
Cell movement
(i) There is an ongoing discussion as to what the driving force of cell migration in the epithelium is (Wright & Alison 1984, p.724; Kaur & Potten 1986c; Heath 1996). The general mechanisms discussed include active basement membrane flow, mitotic pressure and active cell movement.
(ii) Here, we assume, that the essential mechanism responsible for the day‐by‐day cell flux in the crypt is mitotic activity, which causes a pressure‐driven passive movement. Cells move continuously on the crypt cylinder surface. The movement of a cell is driven by local repelling and attracting forces due to elastic cell–cell and adhesive interactive forces. We assume that these forces can be adequately modelled by a network of springs between neighbouring cells. We further assume that motion is overdamped due to strong friction. This leads to first‐order dynamics. Cells cannot be pushed out of the bottom of the crypt, and due to the external constraint, movement is anisotropic. Cells that move over the crypt upper horizon are removed.
(iii) The total force acting on a cell i is equal to the sum of all forces coming from the springs of all neighbouring cells j connected to i:
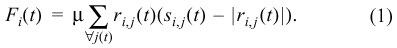
µ is the spring constant, ri ,j is the vector from i to j and ri,j(t ) is the corresponding unit vector. The effective displacement within a small time interval Δ_t_ in the overdamped limit (inertial terms small compared to dissipative terms; see Drasdo 2000) is calculated by
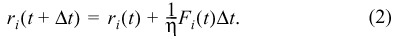
ri is the vector of the centre of cell i and η is the damping constant.
After any displacement of the cell positions, the Delaunay neighbourhoods may have changed, so the triangulation process has to be redone for every time step.
Cell mobility is described by λ = µ/η. λ influences the velocity of the relaxation process. A small λ tends to jam the crypt and a high value leads to unrealistically fast cell mobility. Simulations showed that a λ of 0.01 with a time step Δ_t_ of 30 s is suitable. Small deviations from these values had no noticeable impact on the simulation results.
The url given at the end of this paper links to an online animation of the simulated model crypt.
Cell pedigree concept
(i) The pedigree concept was described in detail previously in Loeffler et al. (1986) and is used in this sense in the following. However, due to the smaller number of cells in a model crypt the number of transit cell divisions per stem cell had to be redetermined.
(ii) The number N(S) and position of stem cells (S) in the unperturbed, steady state are fixed in each crypt. Stem cells are assumed to lie directly on top of the Paneth cells and to divide strictly asymmetrically. Dividing transit cells (T) undergo a fixed number of symmetrical divisions L(T) and then become non‐dividing cells. With regard to mechanical properties, all cells are treated alike.
(iii) N(S), L(T) and the stem cell cycle T C(S) in hours are coupled by P day, the production of cells per day: P day = N(S)2_L_(T)24/T C(S).
Cell kinetics
(i) Cell kinetic parameters for cells in intestinal crypts in lower and higher positions were published in Al‐Dewachi et al. (1975), Tsubouchi (1983) and Potten (1986).
(ii) The Paneth and mature cells do not divide. The stem cells are assumed to have cycle times ranging from 12–13 ± 2 h and the transit cell population to have a cycle time of 12 h with a range of 10–14 h. The S‐phase is assumed to last 8 h and the G2‐ and M‐phases 1 h. The duration of the G1‐phase is assumed to vary stochastically, to be uniformly distributed and to generate the entire variation in the cell cycle duration.
(iii) Cell cycle progression is discretized. After cell division a uniformly distributed randomization is used to allocate each cell the duration of its prospective G1‐phase within the limits given above. Division is spatially modelled by splitting the cell point. One cell takes over the position of the mother cell and the other is placed randomly nearby. We have made no assumptions about the mitotic axis and the arrangement of the new cells within the tissue, but leave this to the movement process.
Assumptions on scoring techniques
Sectioning and scoring
(i) Sections of gut samples were cut at a thickness of about 3–5 µm. Crypts were selected for scoring if they were clearly longitudinally sectioned as identified by the presence of a lumen and Paneth cells at their bases. The sectioned cell nuclei were numbered in the crypts, starting with cell position 1 at the mid‐point of the crypt base and continuing up one side to the neck of the crypt (Kaur & Potten 1986b).
(ii) The model crypts were geometrically cut by a randomly chosen longitudinal section that cuts both the crypt bottom and the upper orifice of the cylinder. We assumed cell nuclei to be circular with the cell points in their centres. A model nucleus was considered to be sectioned if this circle was cut. Sectioned nuclei were sorted according to their vertical position within the crypt and were numbered with the lowest cell defined to be at position 1.
(iii) Section thickness corresponds to about 3 µm.
Labelling, positional label index, positional mitotic index, runs and positional velocity
We stick to the assumptions made in Loeffler et al. (1986):
(i) Tritiated thymidine 3HTdR is incorporated into the cell DNA within the S‐phase. When labelled cells divide, two labelled daughter cells originate. With repeated divisions the label will be diluted and may not be recognized (below the detection level).
(ii) All cells in the S‐phase are marked equally and immediately. The marker is transferred to all daughter cells after division. Dilution of the label is not considered, since, on the whole, short time scales, that is, shorter than one cell cycle, are involved. Paneth cells were assumed to remain unlabelled. Mature cells cannot initially be labelled, but labelled transit cells can become labelled mature cells in the course of time. Cells are counted as mitotic when their cell cycle is in the M‐phase.
(iii) As the simulation produces the same data output as the experiment, all evaluations mentioned (pLI, pMI, Runs) can be made in a similar fashion. The positional velocity values are calculated by comparing the percentiles of two pLI curves from different time points after labelling in the manner shown in Qiu et al. (1994).
Clonal markers, clones and cell trajectories
(i) Clonal analysis of the intestinal epithelium became possible with application of mutagens such as N‐nitroso‐N‐ethylurea (NEU), which induced a mutation at the _D_1_b_–1 locus yielding different staining (Dolichos biflorus lectin binding) for affected cells and their clones in heterozygous mice (Winton et al. 1988; Park et al. 1995; Bjerknes & Cheng 1999; Fig. 1(c) from Potten et al. 1997).
(ii) By introducing a heritable hypothetical clonal marker to individual cells, we can actually visualize the development and structure of a clone in the crypt. By tracking the position of a cell with time we can visualize its trajectory.
(iii) In the model it is possible to give each cell an individual marker that is inherited by all its descendant cells. This makes it possible to determine for each cell which stem cell it was derived from.
Simulation
Stochastic elements
Stochastic elements are included in the model. The duration of the G1‐phase is uniformly distributed in a range of 2–4 h, depending on the cell type.
One of the daughter cells of a dividing cell is positioned at a random position a fixed distance of the mother cell away. Simulations show, however, that this initial position has no noticeable influence, although the position changes quickly within the first iterations of the movement process.
The position and angle of simulated crypt sectioning is chosen randomly. Initial positions of Paneth cells and stem cells are in the first step determined by hand, but both cell types may move freely. After a short simulation fore‐run the resulting positions of these cells are fixed.
Simulation procedure
We developed an interactive simulation environment for this model. It is implemented in C++ using a graphical user interface based on X‐Windows/Motif. It is possible to alter all parameters during a running simulation and to watch the simulation process.
The simulation loop proceeds as follows for each iteration step: 1. we determine neighbourhood relationships via Delaunay triangulation; 2. we calculate forces; 3. cells are moved and emigrated cells are removed; 4. cells age and divide. At specific time points, sectioning and scoring are performed. Simulations were performed on Linux workstations.
RESULTS
Spatial arrangement and cell migrations
Figure 2a shows a snapshot of a simulation. The crypt includes the upper row of Paneth cells at the tapered bottom of the crypt. The cell shapes are Voronoi diagrams and are therefore convex polygons. The distribution of the number of neighbours Ni per cell depends only a little on specific parameters and tends to favour hexagonal shapes (N 3 < 1%, N 4 = 5%, N 5 = 20%, N 6 = 56%, N 7 = 18, N ≥8 < 1%). Randomly generated Poisson Voronoi diagrams, in contrast, show a much wider distribution (N 3 = 1%, N 4 = 10%, N 5 = 26%, N 6 = 20%, N 7 = 9%, N 8 3%, N ≥9 < 1%; Okabe et al. 2000, p. 295). This indicates that the dynamic process of cell movement enables cells to develop into a uniform shape as illustrated in Fig. 1a and b.
Figure 2.
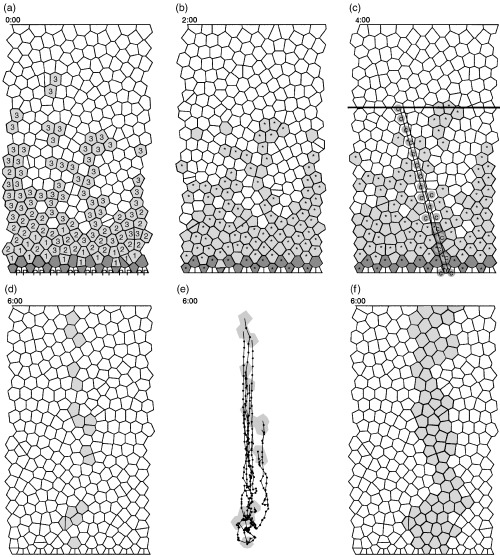
Various simulation snapshots. (a) White non‐differentiating cells, light grey transit cells of shown generation, dark grey stem cells and white Paneth cells, marked with a P. Simulation time t = 0:00. (b) Same simulation at t = 2:00. Cells in S‐phase have been marked by an asterisk. (c) A simulated section at t = 4:00. The S‐phase cells are as in (b). The cell marked with a c represent cells that might occur in a longitudinal section. The black horizontal line marks the crypt–villus junction. (d)–(f) t = 6:00. The grey cells in (d) show a clone from one specific stem cell. The migration trajectories of this clone are shown in (e). The small black dot‐to‐dot distance equals 1 h. (f) shows a combined clone from four neighbouring stem cells.
However, there is a positional dependence of cell size, with cells at the bottom of the proliferative region being smaller and more densely packed than at higher positions. This illustrates that the model is in a dynamic stationary state that is not characterized by relaxation of the inter‐cellular forces (Fig. 3a). This is due to the ongoing mitotic activity and the first‐order movement dynamics. Relaxation can be observed to occur if mitotic activity is blocked. Figure 3b shows how the cell flux decreases gradually after mitotic activity is stopped. Figure 3a shows the relaxation of cell‐to‐cell distances for different time points.
Figure 3.
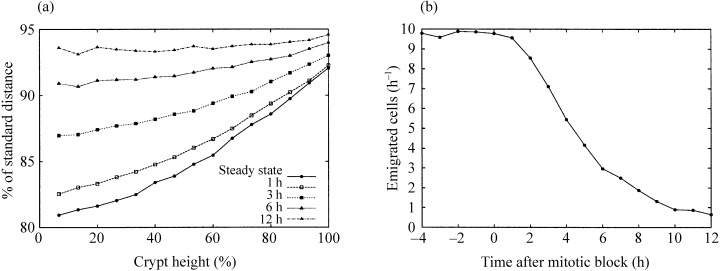
The behaviour of the model crypt at different time points after a simulated mitotic block. (a) The vertical distribution of average cell‐to‐cell distances compared to the standard relaxed distance s. In steady state, cells in lower positions are more compressed than those in upper regions. 12 h later any mitotic activity has ceased and all distances are approximately equal. Vertical positions are measured as percentages of the total model crypt height. (b) For several hours after a mitotic block, at 0 h, cells still leave the crypt as a consequence of the relaxation process.
Figure 2d shows how a single clone spreads over the crypt. The marked cells are all ancestors of one stem cell. A reason for the disruption of this ribbon‐like structure is the unhindered stochastical horizontal migration of all cells. This can be seen in Fig. 2e, where the trajectories of all cells of this clone are shown. Note that cells in the upper regions move upwards in a swarm‐like, directed manner, whereas cells near the bottom move in a much more individualistic fashion. Horizontal and even downward movements can occur. If about a quarter of neighbouring stem cells are marked in this way, a ribbon‐like, non‐disrupted structure with an irregular bounded shape develops (Fig. 2f) that is reminiscent of Fig. 1c.
Simulation of label experiments
3HTdR label experiments were simulated. A set of reference parameters was fixed as shown in Table 2.
Table 2.
Simulation parameter sets. N(S) is the number of stem cells, L(T) is the number of transit cell generations, T(S) is the cell cycle time of stem cells and P day is the resulting cell production per day. T (transit cells) is 12 h for all sets
| N(S) | L(T) | T(S) | P day |
|---|---|---|---|
| 8 | 4 | 13 | 236 |
| 16 | 3 | 13 | 236 best fit, reference |
| 20 | 2.5 | 12 | 226 |
Figure 4 shows simulated positional labelling index curves compared to the corresponding experimental data at 40 min, that is, a flash label (left‐hand panel), and at 9 h after 3HTdR treatment (right‐hand panel). A good fit is obtained with 16 stem cells and a short pedigree. The variants with fewer (a,b) and more stem cells (e,f) did not show such a steep decay in the pLI curve at the top of the proliferative zone.
Figure 4.
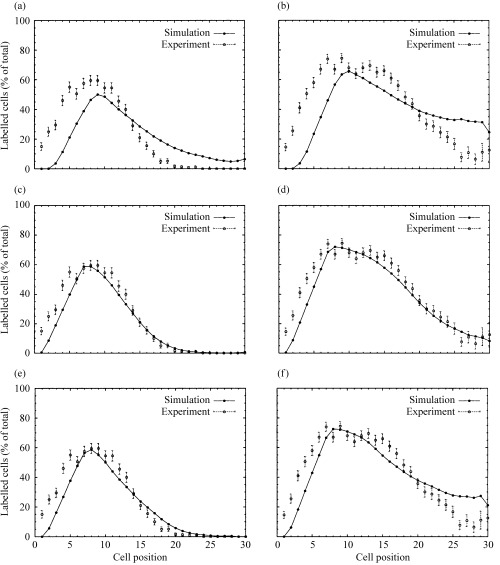
Positional labelling index data for 40 min (left panels: a, c, e) and 9 h (right panels: b, d, f) after 3HTdR labelling for different numbers of stem cells. (a, b) With 8 stem cells; (c, d) with 16 stem cells; (e, f) with 20 stem cells.
A Run measurement for the mixing of adjacent columns based on crypt sections (Loeffler et al. 1986) is shown in Fig. 5. As the distributions vary only a little with different parameter sets, only Run distributions for one parameter set (16 stem cells) are shown. The labelling curves show that the model produces somewhat shorter Runs than observed, suggesting slightly more intermixture between adjacent columns in the model.
Figure 5.
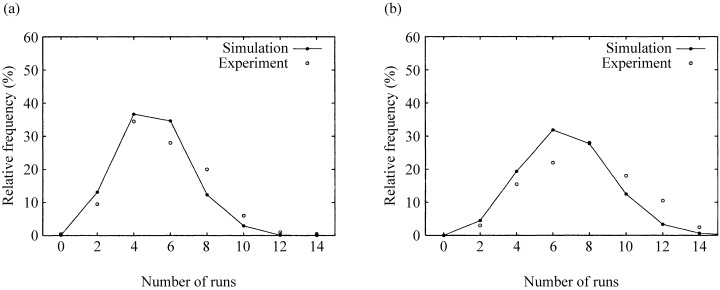
Run distributions comparing simulations with 16 stem cells for the experiment 40 min (a) and 9 h (b) after labelling.
Figure 6a shows simulated positional mitotic index curves for the 16 stem cell variant, which fits the experimental data best. The index increases from position 1 to a maximum of about 5% at positions 6–7 and decreases with a parameter‐dependent steepness. A good fit is also observed for the measurement of cell velocity (Fig. 6b). The underlying experimental pLI curves are those from Fig. 4.
Figure 6. Positional mitotic activity and cell velocity.
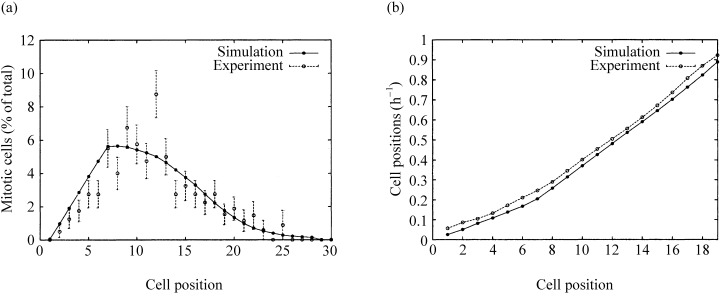
(a) The positional mitotic index using 16 stem cells using a data set of 200 half‐crypt sections from four untreated mice killed at 15:00. (b) Migration velocity data in steady state, simulation versus experimental data. The velocities were calculated from the pLI data sets shown in Fig. 4c and d. The velocity calculations were performed in the way described in Qiu et al. (1994).
A sensitivity analysis shows that there is a distinct but narrow window of acceptable parameters for the number of stem cells and the length of the pedigree.
DISCUSSION
The model presented here is the first lattice‐free model designed to represent the spatial arrangement and migration of cells in the intestinal crypt. Cell movement is characterized by the elasticity between cells and strong friction.
The model parameters may be chosen in line with known cell kinetic facts to achieve a good fit to the experimental data. The best fit is produced when cell migration in the crypt is a laminar flow, which is accomplished by assuming a complete ring of 16 stem cells near the crypt bottom circumference.
In particular, this model implies that local cell sorting rules required in the previous lattice‐based models were not necessary. Furthermore, whenever a cell was born, the lattice‐based models required an entire column of cells to be shifted upwards. Besides the biologically implausible disruption of many next‐neighbour contacts, this model feature induced a long‐distance perturbation of the positional age structure. A local age‐dependent migration process was hence required to adjust for this model artefact. The model presented here removes these artefacts and appears to be much closer to biology and at the same time requires fewer assumptions about cell‐to‐cell interactions. In particular, there is no dependence of the movement on the cell type or age.
The model allows an examination of the geometrical implications of aspects that cannot be included in a non‐spatial model. For example, the influence of the geometrical positions of the Paneth cells and the stem cells has an impact on many positional data (not shown). Moreover, the model provides a much more intuitive and distinct consideration of the measurement process by permitting direct simulations of the sectioning process in which thickness can be considered.
The selection and visualization of cell clones in the model opens up the possibility to investigate much more closely the development of NEU‐induced clones of mutated cells (Winton et al. 1988). The ribbon‐like but irregular and changing shape of these clones can be reproduced by the model. The width of the ribbon is determined by the percentage of affected stem cells. As the mutation of more than one cell per crypt is very unlikely, the conversion to complete monoclonality (Park et al. 1995) needs a relaxation of the model assumptions about the lifelong fixed number of stem cells per crypt. Possible approaches might include the introduction of asymmetrical stem cell divisions (1993, 1997) or ideas from Gerike et al. (1998). Here the number of transit cell divisions is not fixed but controlled by the gradient of a hypothetical growth factor. This can be extended to the stem cell population itself and results in the dropping of the assumptions of a fixed pedigree and fixed number of stem cells.
Cell death was not considered explicitly in this paper. Nevertheless, the model can easily be adapted to deal with the removal of cells to simulate apoptosis, for example. The Voronoi diagram ensures that there will be no holes at any time. The movement process fills the space of a dying cell by smoothly contracting the neighbouring cells.
The model is simplified in several respects. The physical modelling assumptions of the tissue properties are based on unproven assumptions. The model is conceptually constrained to a 2‐D view of the epithelium. The influence of the connective tissue surrounding the crypt is a consideration that is left out. The model crypt is based on a fixed‐size cylinder and cannot change dimensions dynamically. This excludes the simulation of perturbations, which lead to larger changes of the overall crypt size such as seen during post‐irradiation recovery (Paulus et al. 1992).
We left out the modelling of circadian rhythms. Circadian rhythms have a big impact on pLI curves in the small intestine (Qiu et al. 1994). Another point left out here is the modelling of the Goblet cell lineage. Paulus et al. (1993) suggested that Goblet cells derive stochastically from transit cells. This assumption can be included in the lattice‐free model. The new model would allow a finer analysis of the spatial distribution of Goblet cells.
We are currently working on adaptations of our novel model class to other tissues, starting with the murine colonic crypt. Besides the different histology and kinetics, circadian rhythms play an even stronger part here and have to be adequately modelled. Similar modelling approaches may also be useful for other 2‐D tissues such as the cornea and the urogenital or respiratory tract epithelia.
Acknowledgements
We thank V. Werling, who performed some of the simulations, and D. Drasdo and C. Booth for valuable discussions. This work was supported by the Deutsche Forschungsgemeinschaft Lo 342/4–2/3. Additional material and animated sequences of the simulated model can be found at http://www.imise.uni‐leipzig.de/~frank/crypt‐model.
References
- Al‐Dewachi HS, Wright NA, Appleton DR, Watson AJ (1975) Cell population kinetics in the mouse jejunal crypt. Virchows. Arch. B. Cell. Pathol. 18, 225. [DOI] [PubMed] [Google Scholar]
- Al‐Dewachi HS, Appleton DR, Watson AJ, Wright NA (1979) Variation in the cell cycle time in the crypts of Lieberkuhn of the mouse. Virchows. Arch. B Cell Pathol. Incl. Mol. Pathol. 31, 37. [DOI] [PubMed] [Google Scholar]
- Bjerknes M & Cheng H (1999) Clonal analysis of mouse intestinal epithelial progenitors. Gastroenterology 116, 7. [DOI] [PubMed] [Google Scholar]
- Browder LW, Erickson CA, Jeffrey WR (1991) Developmental Biology, 3rd edn Philadelphia: Saunder College. [Google Scholar]
- Chwalinski S & Potten CS (1989) Crypt base columnar cells in ileum of BDF1 male mice–their numbers and some features of their proliferation. Am. J. Anat. 186, 397. [DOI] [PubMed] [Google Scholar]
- Drasdo D (2000) Buckling instabilities of one‐layered growing tissues. Phys. Rev. Lett. 84, 4244DOI: 10.1103/physrevlett.84.4244 [DOI] [PubMed] [Google Scholar]
- Finney KJ, Appleton DR, Ince P, Sunter JP, Watson AJ (1989) Proliferative status of colonic mucosa in organ culture: 3H‐thymidine‐labelling studies and computer modelling. Virchows Arch. B Cell Pathol. Incl. Mol. Pathol. 56, 397. [DOI] [PubMed] [Google Scholar]
- Gerike TG, Paulus U, Potten CS, Loeffler M (1998) A dynamic model of proliferation and differentiation in the intestinal crypt based on a hypothetical intraepithelial growth factor. Cell Prolif. 31, 93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guibas LJ & Stolfi J (1985) Primitives for the manipulation of general subdivisions and the computation of Voronoi diagrams. ACM Trans. Graphics 4, 74. [Google Scholar]
- Heath JP (1996) Epithelial cell migration in the intestine. Cell Biol. Int. 20, 139DOI: 10.1006/cbir.1996.0018 [DOI] [PubMed] [Google Scholar]
- Honda H (1978) Description of cellular patterns by Dirichlet domains: the two‐dimensional case. J. Theor. Biol. 72, 523. [DOI] [PubMed] [Google Scholar]
- Isele WP & Meinzer HP (1998) Applying computer modeling to examine complex dynamics and pattern formation of tissue growth. Comput. Biomed. Res. 31, 476DOI: 10.1006/cbmr.1998.1490 [DOI] [PubMed] [Google Scholar]
- Kaur P & Potten CS (1986a) Cell migration velocities in the crypts of the small intestine after cytotoxic insult are not dependent on mitotic activity. Cell Tissue Kinet. 19, 601. [DOI] [PubMed] [Google Scholar]
- Kaur P & Potten CS (1986b) Circadian variation in migration velocity in small intestinal epithelium. Cell Tissue Kinet. 19, 591. [DOI] [PubMed] [Google Scholar]
- Kaur P & Potten CS (1986c) Effects of puromycin, cycloheximide and noradrenaline on cell migration within the crypts and on the villi of the small intestine. A model to explain cell movement in both regions. Cell Tissue Kinet. 19, 611. [DOI] [PubMed] [Google Scholar]
- Loeffler M & Potten CS (1997) Stem cells and cellular pedigrees – a conceptual In: Potten CS, ed. Stem Cells, p. 1 London: Academic Press. [Google Scholar]
- Loeffler M, Stein R., Wichmann HE, Potten CS, Kaur P, Chwalinski S (1986) Intestinal cell proliferation. I. A comprehensive model of steady‐state proliferation in the crypt. Cell Tissue Kinet. 19, 627. [DOI] [PubMed] [Google Scholar]
- Loeffler M, Potten CS, Paulus U, Glatzer J, Chwalinski S (1988) Intestinal crypt proliferation. II. Computer modelling of mitotic index data provides further evidence for lateral and vertical cell migration in the absence of mitotic activity. Cell Tissue Kinet. 21, 247. [DOI] [PubMed] [Google Scholar]
- Loeffler M, Birke A, Winton D, Potten C (1993) Somatic mutation, monoclonality and stochastic models of stem cell organization in the intestinal crypt. J. Theor. Biol. 160, 471DOI: 10.1006/jtbi.1993.1031 [DOI] [PubMed] [Google Scholar]
- Loeffler M, Bratke T, Paulus U, Li YQ, Potten CS (1997) Clonality and life cycles of intestinal crypts explained by a state dependent stochastic model of epithelial stem cell organization. J. Theor. Biol. 186, 41DOI: 10.1006/jtbi.1996.0340 [DOI] [PubMed] [Google Scholar]
- Meinzer HP, Sandblad B, Baur HJ (1992) Generation‐dependent control mechanisms in cell proliferation and differentiation‐the power of two. Cell. Prolif. 25, 125. [DOI] [PubMed] [Google Scholar]
- Okabe A, Boots B, Sughihara K (2000) Spatial Tesselations: Concepts and Applications of Voronoi Diagrams, 2nd edn Chichester: John Wiley and Sons. [Google Scholar]
- Park HS, Goodlad RA, Wright NA (1995) Crypt fission in the small intestine and colon. A mechanism for the emergence of G6PD locus‐mutated crypts after treatment with mutagens. Am. J. Pathol. 147, 1416. [PMC free article] [PubMed] [Google Scholar]
- Paulus U, Potten CS, Loeffler M (1992) A model of the control of cellular regeneration in the intestinal crypt after perturbation based solely on local stem cell regulation. Cell Prolif. 25, 559. [DOI] [PubMed] [Google Scholar]
- Paulus U, Loeffler M, Zeidler J, Owen G, Potten CS (1993) The differentiation and lineage development of goblet cells in the murine small intestinal crypt: experimental and modelling studies. J. Cell Sci. 106, 473. [DOI] [PubMed] [Google Scholar]
- Potten CS (1986) Cell cycles in cell hierarchies. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 49, 257. [DOI] [PubMed] [Google Scholar]
- Potten CS & Loeffler M (1987) A comprehensive model of the crypts of the small intestine of the mouse provides insight into the mechanisms of cell migration and the proliferation hierarchy. J. Theor. Biol. 127, 381. [DOI] [PubMed] [Google Scholar]
- Potten CS, Chwalinski S, Swindell R., Palmer M (1982) The spatial organization of the hierarchical proliferative cells of the crypts of the small intestine into clusters of ‘synchronized’ cells. Cell Tissue Kinet. 15, 351. [DOI] [PubMed] [Google Scholar]
- Potten CS, Roberts SA, Chwalinski S, Loeffler M, Paulus U (1988) Scoring mitotic activity in longitudinal sections of crypts of the small intestine. Cell Tissue Kinet. 21, 231. [DOI] [PubMed] [Google Scholar]
- Potten CS, Booth C, Pritchard DM (1997) The intestinal epithelial stem cell: the mucosal governor. Int. J. Exp. Pathol. 78, 219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu JM, Roberts SA, Potten CS (1994) Cell migration in the small and large bowel shows a strong circadian rhythm. Epithelial Cell Biol. 3, 137. [PubMed] [Google Scholar]
- Tsubouchi S (1983) Theoretical implications for cell migration through the crypt and the villus of labelling studies conducted at each position within the crypt. Cell Tissue Kinet. 16, 441. [PubMed] [Google Scholar]
- Winton DJ, Blount MA, Ponder BA (1988) A clonal marker induced by mutation in mouse intestinal epithelium. Nature 333, 463. [DOI] [PubMed] [Google Scholar]
- Wright N & Alison M (1984) The Biology of Epithelial Cell Populations, Vols 1 & 2 Oxford: Clarendon Press. [Google Scholar]