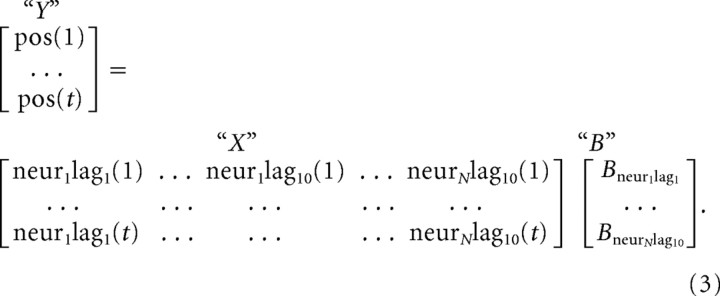Single-Neuron Stability during Repeated Reaching in Macaque Premotor Cortex (original) (raw)
Abstract
Some movements that animals and humans make are highly stereotyped, repeated with little variation. The patterns of neural activity associated with repeats of a movement may be highly similar, or the same movement may arise from different patterns of neural activity, if the brain exploits redundancies in the neural projections to muscles. We examined the stability of the relationship between neural activity and behavior. We asked whether the variability in neural activity that we observed during repeated reaching was consistent with a noisy but stable relationship, or with a changing relationship, between neural activity and behavior. Monkeys performed highly similar reaches under tight behavioral control, while many neurons in the dorsal aspect of premotor cortex and the primary motor cortex were simultaneously monitored for several hours. Neural activity was predominantly stable over time in all measured properties: firing rate, directional tuning, and contribution to a decoding model that predicted kinematics from neural activity. The small changes in neural activity that we did observe could be accounted for primarily by subtle changes in behavior. We conclude that the relationship between neural activity and practiced behavior is reasonably stable, at least on timescales of minutes up to 48 h. This finding has significant implications for the design of neural prosthetic systems because it suggests that device recalibration need not be overly frequent, It also has implications for studies of neural plasticity because a stable baseline permits identification of nonstationary shifts.
Keywords: premotor, arm, macaque, multielectrode array, decoding, brain machine interface
Introduction
Some natural behaviors are repeated frequently, with little variation, whereas other movements are novel and tailored to the current circumstance. It is an open question whether repeated movements are accomplished with similar neural activity patterns or whether the brain uses somewhat different neural activity patterns to generate similar behaviors. By using chronically implanted multielectrode arrays, investigators can simultaneously monitor many neurons over several hours (Jones et al., 1992; Nicolelis et al., 1997; Williams et al., 1999; Wise et al., 2004; Santhanam et al., 2006). We performed multielectrode array recordings in the dorsal aspect of the macaque premotor cortex (PMd) as well as primary motor cortex (M1) to ask whether the neural responses that give rise to similar behaviors are stable or change over time.
This question has relevance for both basic neuroscience and the development of brain-machine interfaces (BMIs). Several studies suggest that the neuron–behavior relationship remains stable across days (Schmidt et al., 1976; Greenberg and Wilson, 2004), and such stability is an implicit assumption in many neurophysiology studies. In contrast, Padoa-Schioppa et al., (2004) found significant shifts in the preferred directions (PDs) of the neurons during an experimental session. Also, computational models have been developed around the concept of neural circuits using single neurons in different ways over time (Maass et al., 2002) or changing tuning readily (Abbott and Blum, 1996; Rokni et al., 2007).
In the development of BMIs, the stability of the neuron–behavior relationship is a crucial design parameter. In BMI studies, a decoder that uses neural activity to infer arm movement behavior is typically built at the beginning of the experiment and then applied across the entire experimental session, often several hours. In support of a stable neuron–behavior relationship, Serruya et al. (2003) reported good performance across 2 d using the same decoder. Similarly, Musallam et al. (2004) predicted movement parameters using both fixed and adaptive neural prosthetic decoders and found no improvement with adaptive decoders. In contrast, Carmena et al. (2005) found that the contributions of individual neurons to the decoder varied dramatically over time, suggesting that neurons changed their relationship to the behavior. Thus, there is evidence from basic science and neural prosthetic experiments both for and against the notion that neural activity in PMd and M1 makes a stable contribution to behavior.
To examine this issue, the relationship between behavior and neural activity in caudal PMd and rostral M1 was examined while three rhesus macaques performed various reaching tasks for multiple hours. In two animals, data were also examined across multiple days. For each neuron across time, we measured (1) average firing rate for similar reaches, (2) preferred direction, and (3) the contribution of the neuron to a linear decoder of hand position. Our results suggest that the relationship between neural activity and reaching-arm behavior is reasonably stable on a timescale from minutes to 48 h.
Parts of this work have been published previously in abstract form (Chestek et al., 2006).
Materials and Methods
Animal behavior.
All protocols were approved by the Stanford University Institutional Animal Care and Use Committee. We trained three rhesus macaques (G, H, and L) to perform reaches to visual targets projected onto a frontoparallel screen (Fig. 1 A). Reaches were performed in complete darkness except for the illuminated target. Hand position was optically tracked with infrared reflective tape attached to the distal digit of the index figure and measured at 60 samples/s (nominal submillimeter resolution) using a Polaris system (Northern Digital, Waterloo, Ontario, Canada). Eye position was tracked optically using Iscan (Iscan, Burlington, MA). In monkeys G and H, fixation was enforced throughout the plan period to control for potential eye-position modulations on activity in PMd (Batista et al., 2007, 2008).
Figure 1.
Experiment setup. A, Animals sat facing a frontoparallel workspace looking at and touching a central target while preparing to reach for a peripheral target. B, Hand trajectories for monkey H, center-out delayed reach task. C, Trajectories for monkey L, grid task. D, Multiple waveforms on one electrode. Blue waveform sorted as very good isolation. E, Example of mean firing rate for repeated reaches to the same target for monkey H. Red line denotes linear regression fit. F, Example of tuning curve for monkey H split into first half (blue) and last half (magenta) of trials. Cosine fits also shown with PD denoted by line. Error bars denote SE. (No significant shift.)
Three monkeys performed many repetitions of the task across many weeks with simultaneous neural recordings. For analysis, we selected main datasets in which the monkeys worked for >1000 trials (which was typical, but not always the case) to have sufficient trial count and span of time to facilitate the present analyses. In this study, we used a total of five single-day datasets for three separate analyses, which are explained in detail below. To summarize, changes across the normal length of experiments (∼0.5–2 h) were examined using two datasets from monkeys G and H and a subset of a very large dataset from monkey L. The complete large dataset for monkey L was used in a second analysis to look at changes across 6.4 h. Finally, an additional two datasets from 1 d before the main dataset in monkey H and 2 d previous in monkey G were used to evaluate stability across days.
Monkeys G and H performed a “center-out” reach task (Georgopoulos et al., 1982; Churchland et al., 2006c). At the start of each trial, a touch point was illuminated at approximately shoulder height. After 400–700 ms, a peripheral target appeared at one of eight locations surrounding the touch point at a radius of 10 cm. Target location was random within blocks of eight. After a plan period of 750 or 1000 ms (randomized), the touch point was extinguished, and the peripheral target increased in size as the GO cue. To ensure that the monkey started planning immediately, one-third of the trials were “catch” trials, with plan periods 200 ms long, which were not analyzed in the present study. After the GO cue, the monkey was required to begin a reach within 400 ms. The criterion for when the hand was moving was a hand speed >0.2 m/s after filtering the velocity to remove high-frequency noise in the measurement. Average movement times were 240 and 280 ms for G and H. After reaching the target within 750 ms, the monkey was required to hold the target for 250 ms and then received a liquid reward. Figure 1 B shows 1 min of trajectories from monkey H, illustrating the task. Monkeys G and H performed 1456 and 1072 successful trials over the course of 1.5 and 2.3 h, respectively, taking several brief breaks. In these datasets, 10.0% of the combined trials were unsuccessful and were eliminated before analysis. The errors consisted of the following types: failing to move at all, moving too slowly to hit the target within 750 ms, moving after target onset but before the GO cue, and bringing their hand too far away from the screen out of range of the infrared camera during the reach. Also, an additional 856 similar reaches from 2 d previous in monkey G and 552 similar reaches from 1 d previous in monkey H were used in a multiday comparison.
The third animal, monkey L, performed a “grid” task, in which he reached to randomly selected targets at one of 25 locations (15 × 15cm grid) as they appeared, each reach beginning where the last left off. Figure 1 C illustrates this task with 1 min of the reach trajectories. This represents an intermediate case between the highly stereotyped reach task used with monkeys G and H and the gridless random target placement tasks like those in the studies of Paninski et al. (2004) and Carmena et al. (2005). The animal had to complete each reach within 750 ms after the GO cue, but the average reach duration was 480 ms. A total of 8.5% of the trials were unsuccessful and were eliminated before analysis. This animal performed 12,982 successful trials over 6.4 h, electing to take 15 breaks up to 8 min in length at various times. This animal generally reaches eagerly, and this represents the longest contiguous dataset available from our experiments. All animals were well trained on their tasks, having performed tens of thousands of trials over 2–6 months before data were collected. Table 1 summarizes the speed and consistency of reaching behavior during successful trials for each animal. When directly comparing data for all three animals, 1000 reaches were used from each of the three datasets. When analyzing monkey L separately, the entire set of 12,982 trials was used. Monkeys G and H have also participated in other studies (Churchland et al., 2006a,c; Santhanam et al., 2006; Batista et al., 2007; Yu et al., 2007).
Table 1.
Behavior statistics (mean ± SD)
| Start point error (mm) | Reactiontime (ms) | Movementtime (ms) | Average speed (mm/s) | End pointerror (mm) | |
|---|---|---|---|---|---|
| Monkey G (center out) | 11.3 ± 3.6 | 236.9 ± 23.4 | 244.6 ± 41.8 | 404.3 ± 67.4 | 8.7 ± 3.3 |
| Monkey H (center out) | 5.6 ± 2.9 | 247.6 ± 22.2 | 278.5 ± 39.3 | 355.2 ± 51.2 | 5.4 ± 2.7 |
| Monkey L (grid) | 373.5 ± 112.5 | 480.6 ± 103.3 | 169.8 ± 83.9 | 13.8 ± 3.1 |
Electrophysiology and behavioral recordings.
A commercially available 96-channel silicon electrode array (Cyberkinetics, Foxborough, MA) was implanted into PMd/M1 of each animal using standard neurosurgical techniques (Hatsopoulos et al., 2004). Arrays were placed rostrocaudally between the central and arcuate sulci and mediolaterally between the spur of the arcuate sulcus and the precentral dimple [supplemental figure of Santhanam et al. (2006) contains array implantation photographs for monkeys G and H[. Arrays were implanted contralateral to the arm used to perform the task. Neural data were recorded using a Cerebus system (Cyberkinetics). Single units were isolated off-line using the Sahani spike sorting algorithm (Sahani, 1999; Santhanam et al., 2004). A total of 65 unit isolations were judged to be “very good” (17, 31, and 17 from monkeys G, H, and L, respectively). Figure 1 D shows an example. The firing rate and tuning curve analyses used these units. An additional 11, 25, and 28, respectively, “good” isolations were included in the linear decoder analyses. For the multiday analysis, spike sorting was performed as described above. Then, two independent observers matched units by size and isolation from other units across days. Only “high-confidence” matches agreed on by both observers were evaluated. These included 24 units of the original 48 for monkeys G and H. For an example of two matched units, see Figure 4, A and B. Ideally, neurons would be recorded overnight, to statistically certify unit correspondence. This is now technically possible for future studies using two electrodes at a time (Santhanam et al., 2007).
Figure 4.

Stability over multiple days in monkeys G and H. A, Change in firing rate across multiple days, using 1552 and 1856 reaches for monkeys G and H for all neuron–direction pairs. B, Shift in preferred direction between first day and last day of analysis (2 d separation for monkey G, 1 d separation for monkey H). C, Linear model performance across days for monkey G (top) and monkey H (bottom). D, Example of tuning curve shifts in monkey G (left) and monkey H (right) with significant (top) and insignificant (bottom) changes. Error bars denote SE. Cosine fits also shown, and PD is denoted by line. E, Example of matched unit waveforms on the same electrode across 2 d. Blue and green units were matched by independent evaluation, whereas the red unit was not.
Analysis 1: firing rate over repeated reaches.
We explored whether average firing rate changed over time for reaches to the same targets (or directions for monkey L). Mean firing rate was measured over a perimovement epoch extending from 200 ms before to 300 ms after movement onset. For monkeys G and H, who performed a delayed reach task, mean firing rate was also obtained during a plan period epoch starting 150 ms after the target was presented and ending 500 ms later before the GO cue was given. Monkey L was not included in any plan period analyses because his task did not involve an enforced delay period. Because we average perimovement activity over a long window to get a stable measurement, average firing rates are considerably lower than their peak values. Perimovement and plan period epochs were analyzed separately. Changes in firing rate were identified between the first half and last half of trials for all reaches in each of eight directions. For the grid task, there were 600 possible trajectories (25 starting points × 24 end points), which were pooled into eight bins according to the angle of the trajectory from the previous target, without regard to distance. Such binning was necessary to compare all three animals and should only increase the amount of observed instability. Distances are uniformly sampled, and this helps reduce any instability attributable to the non-uniformity in direction sampling. A t test was then performed on firing rate between the first half and last half of trials for all neuron target pairs with average firing rate >2 Hz. To determine the proportion of significant effects with multiple comparisons, we used a p value correction method described by Simes (1986) to control the false discovery rate (FDR), or the proportion of falsely rejected null hypotheses (Benjamini and Hochberg, 1995). Also, a bootstrap distribution was computed by randomly resampling the firing rate data many times with replacement. The difference in mean firing rate between the first half and last half of this resampled data are plotted along with the measured changes. Figure 1 E shows an example of mean firing rate for a single neuron across 125 reaches in the same direction spread across the experiment. Similarly, for the multiday comparison, a t test was used to determine whether the two days had different mean firing rates for a given neuron–direction pair (p < 0.05, FDR corrected).
Analysis 2: preferred direction.
Tuning curves were estimated by plotting average firing rates as a function of target angle. Perimovement and plan epochs were analyzed separately. A minimal tuning depth of >2 Hz was required for inclusion of neurons, which was available in 43 of the 65 very-good-quality single units. PD was calculated by fitting the tuning curve with a sine and cosine (Georgopoulos et al., 1982; Churchland et al., 2006b; Churchland and Shenoy, 2007) as in Equations 1 and 2, where θ corresponds to reach angle, and f corresponds to firing rate across different angles. The coefficients in B were determined by regression:
Tuning curves were constructed using the first and second half of the data or the first and second day, and changes in PD were measured between them. Figure 1 F shows example tuning curves constructed using the first half of the trials (blue) and second half of the trials (magenta), along with the cosine fits and the estimated preferred directions (short vertical lines). Statistical significance of changes in PD were determined with a bootstrap analysis. First, for each neuron, firing rates were resampled many times to create distributions of PDs within the first half and within the last half of the trials. The means of these distributions were subtracted to simulate the null hypothesis of identical means, and a distribution of changes was found by sampling one PD from each distribution, subtracting these PDs, and then repeating 1000 times to form a PD difference distribution. The measured change was then compared with this distribution to determine a p value. To determine the percentage of significant shifts with multiple comparisons, the FDR Bonferroni's-type correction described above was used with p < 0.05. The bootstrap PD differences across the entire population also provide a baseline with which the magnitude of significant effects can be compared.
Analysis 3: linear model performance.
We built models that could linearly reconstruct the reach trajectory using neural activity, as by Carmena et al. (2005). The spike count was measured during 100 ms bins. Position and velocity in the horizontal and vertical dimensions were averaged during 100 ms bins from 1160 ms before to 340 ms after movement onset for monkeys G and H, and the entire trial for monkey L. The linear model used the firing rates of the neurons at 10 sequential 100 ms time lags (Eq. 3). Kinematic variables were modeled as a function of firing rate using a linear Wiener filter, determined by a multidimensional linear regression. In Equation 3, the firing rate matrix X has 10 columns for each neuron, and the desired kinematic variable, for example x position, is found in matrix Y. Both X and Y have rows corresponding to the total number of 100 ms bins in the experiment. The resulting linear decoder, matrix B, is computed through linear regression as shown in Equation 3. This is the algorithm used by Serruya et al. (2002), Carmena et al. (2005), and Hochberg et al. (2006) with small differences:
The dataset is not contiguous, because the animals made some errors, took a few breaks, and hand position could not be tracked reliably until the touch point was acquired at the start of the trial. Thus, for a given trial, the linear model had access to the current firing rate and 1 s of past firing rate, with zeros for time periods before the trial began. The average length of a trial was 2.2 s for monkeys G and H and 0.99 s for monkey L. The linear model provides a scalar multiplier for each time lag and for each neural unit in the matrix B, which can then be used to predict kinematic variables from firing rate.
Models for individual neurons (B) were created for all kinematic parameters (Y): horizontal and vertical position and velocity. We assessed stability in the neuron–behavior relationship by building models using subsequent 10 min epochs throughout the dataset and then testing them using the same fixed 5 min epoch of behavioral data at the end of the experiment, similar to Carmena et al. (2005). The first decoder analysis used 1000 reaches from three monkeys with a 30 s sliding step between epochs, whereas the second used 12,982 reaches from monkey L only, and the sliding step was 10 min, which resulted in nonoverlapping epochs. Finally, the multiday analysis used 1856 reaches from monkey H and 1552 reaches from monkey G, with a similar sliding step of 30 s for 10 min epochs within days but not between days. All models were tested against 5 min from the end of the second day. Performance of these models was measured using the correlation coefficient ρ and the normalized squared error between the predictions by the model of hand parameters and their measured values. Models were also created and evaluated using the full ensemble of neurons.
Residual behavioral trends.
We examined whether small changes in neural firing rate over time correlate with small changes in behavior over time. To determine whether these correlations could account for some of the firing rate changes, we performed a multiple linear regression using three behavioral measures (reaction time, mean velocity, and end-point y error) as predictor variables or time alone as the predictor variable, and firing rate as the result variable. Also, the partial correlation coefficient between firing rate and time was found, controlling for these three behavioral variables. The amount of variance explained by these models was compared to assess the effect of time relative to the effect of small behavioral changes.
Results
Relationship between neural activity and behavior
Figure 2 summarizes the relationship between neural activity and behavior for all three animals. Neural data collected during 1000 successful reaches from each animal were evaluated according to average firing rate, preferred direction, and linear decoder performance. These reaches were performed over 76, 140, and 27 min, for monkeys G, H, and L. Figure 2A shows a histogram of changes in perimovement firing rates across all neuron–direction pairs and all three animals, normalized to the average firing rate. Results were similar across monkeys when tested individually. There are statistically significant changes in 12.0% of 326 neuron–direction pairs with firing rate >2 Hz (p < 0.05, FDR corrected). The absolute magnitudes of these changes (denoted in red) are quite small when a bootstrap analysis (green line) is considered. The median absolute change normalized to the average firing rate was 7.4%, which represents a small but significant difference from a 4.4% median change in the bootstrap analysis (p < 0.05). The mean overall change in firing rate was 0.0% across the dataset with a SD of 16.2%, as shown in Table 2. Supplemental Figure 1 (available at www.jneurosci.org as supplemental material) shows similar results for plan period activity in monkeys G and H, in which 23% of 135 neuron–target pairs have significant shifts. In that analysis, the median absolute change was 15% compared with 7% for the bootstrap analysis (p < 0.05).
Figure 2.

Stability of neuron–behavior relationship. A, Change in firing rate across 1000 reaches for all neuron–direction pairs for monkeys G, H, and L between first half and last half of trials, normalized to average rate. B, Shift in preferred direction between first and last half of trials. C, Linear model performance for monkey H. ρ value indicates correlation between parameters predicted using each test epoch (abscissa) and final 5 min of behavior. Neurons are sorted by ρ value in epoch 1 on the ordinate. D, Behavioral trends for repeated reaches to one target (monkey H). Red star, Statistically significant trends. E, Error between predicted and measured hand position as a function of time between model generation and test, normalized to the value closest to test set.
Table 2.
Statistics of changes in firing rate and PD
| Firing rate change | PD change | |||||
|---|---|---|---|---|---|---|
| Median absolute (%) | Mean absolute ± SD (%) | Mean ± SD (%) | Median absolute (degrees) | Mean absolute ± SD (degrees) | Mean ± SD (degrees) | |
| 1000 reach perimove dataset | 7 | 11 ± 12* | 0 ± 16 | 5.7 | 9.5 ± 14.6* | −0.7 ± 17.5 |
| 1000 reach perimove bootstrap | 4 | 7 ± 7 | 0 ± 10 | 3.3 | 6.1 ± 8.9 | 0.0 ± 10.8 |
| 1000 reach plan period dataset | 15 | 20 ± 16* | 4 ± 25* | 6.0 | 7.2 ± 7.0 | 1.0 ± 10.2 |
| 1000 reach plan period bootstrap | 7 | 10 ± 10 | 0 ± 14 | 2.7 | 4.8 ± 5.9 | 0.0 ± 7.6 |
| 12,982 reach dataset | 15 | 18 ± 14* | −17 ± 15* | 3.9 | 6.5 ± 6.1* | 3.9 ± 8.1* |
| 12,982 reach bootstrap | 1 | 2 ± 2 | 0 ± 3 | 1.5 | 2.2 ± 2.2 | 0.0 ± 3.1 |
| Multiday dataset | 30 | 37 ± 27* | 31 ± 33* | 9.9 | 11.4 ± 9.8* | 1.4 ± 15.5 |
| Multiday bootstrap | 5 | 7 ± 6 | 0 ± 10 | 2.4 | 3.9 ± 4.4 | 0.0 ± 5.9 |
Figure 2B shows the shift in preferred direction between the first half and the second half of the 1000 reaches, for 43 neurons with tuning depth >2 Hz. Again, shifts were very small, with a median absolute shift of 5.7° compared with 3.3° for the bootstrap analysis. Only 2 of 43 shifts were statistically significant (p < 0.05, FDR corrected) with magnitudes of −33.1 and 7.6°. For plan period activity, the median absolute shift was 6.0° compared with 2.7° for the bootstrap analysis. Also, 2 of 21 units had statistically significant shifts of −6.0 and 6.7° (_p_ < 0.05, FDR corrected), as shown in supplemental Figure 1_B_ (available at www.jneurosci.org as supplemental material). Comparing the first third to the last third of the dataset instead, 5 of 43 neurons had small but statistically significant shifts (_p_ < 0.05, FDR corrected) of 7.5, 11, 21, 28, and −43°. All significant shifts were smaller than 45°, which was the spacing between targets. The size of the firing rate changes and preferred direction shifts were not significantly correlated with whether the neuron was closer to M1 or PMd on the array (_p_ > 0.05 in both monkeys G and H).
We built a linear decoder that predicts reach kinematics from neural data (see Materials and Methods) and then examined whether the contribution of individual neurons to decoder performance changed over time. Decoders were trained during successive 10 min epochs of neural and behavioral data and then tested in their ability to reconstruct the final 5 min of behavioral data. Figure 2C shows a representative example of this analysis performed using one monkey's neural data and one behavioral parameter. The figure depicts the decoding performance of each individual neuron, assessed as the correlation coefficient between the predicted and the actual kinematic parameter in the test data. The abscissa depicts the epoch used to train the model. Along the ordinate, neurons are sorted by their performance during the first epoch, similar to Carmena et al., (2005). It is evident from the strong horizontal color banding that the contribution of individual neurons stays very stable over time. The average absolute ranking change between the first and last training epoch is 1.0 of a possible 54, with an SD of 1.6. Results were nearly identical across monkeys and across kinematic parameters, which include position and velocity in both the horizontal and vertical dimensions. Supplemental Figure 2 (available at www.jneurosci.org as supplemental material) shows results for all four kinematic parameters in one animal.
Correlation between residual neural changes and residual behavioral changes
Several neurons did exhibit statistically significant changes in firing rate and tuning across 1000 reaches, although the magnitudes of these effects were small. This results in an increase in the error between the actual and predicted kinematic parameters for models generated further back in time from the test set (which was the final 5 min). For monkeys G, H, and L, the total squared error of the ensemble decoder increased by 4.3, 19, and 21% between the first and last training set. Figure 2E plots model prediction error as a function of the time between training and testing for the three best-performing neurons (from each animal) in the linear decoder.
This increase in prediction error may be attributable to changes in the relationship between neural activity and behavior. Alternatively, it may be that this relationship is fixed but animals' behavior changes over time, although still within the bounds set for correct task performance. A linear model captures an approximate relationship within a limited range of values, so decoder performance may decline outside of that range. Figure 2D shows a series of kinematic variables calculated for repetitions of individual trial types plotted as a function of repetition number. Despite being highly practiced at this task over months of training, performance was not (and cannot be) perfectly stationary. Significant trends include a decrease in average velocity (∼50 mm/s) and a droop in hand position (up to 10 mm). These correlations were not uniform across targets. For example, end point hand droop was higher for targets above the midline. A total of 66% of neurons have significant correlations with one or more of these parameters (p < 0.05, Bonferroni corrected within all of the comparisons done for a single neuron).
To estimate how much of the trends in firing rate over time could be accounted for by correlations with other behavioral variables, multiple linear regression was performed using several behavioral parameters along with time to predict firing rate. When regressing firing rate versus time alone, time accounted for 2.4% of the variance in firing rate (mean across all neuron–target pairs, maximum 28%). Using multiple regression to control for the effects of reaction time, mean velocity, and end-point _Y_-error reduced variance explained to an average of 2.0% (maximum 20.1%). For comparison, these three behavioral measures alone (without time) account for an average of 5.1% of the variance (maximum 37%). One might have expected the small uncontrolled residual changes in behavior to explain only a small percentage of the variance in firing rate, but this amount is twice as large as the amount explained by time alone. Thus, the effect of time on firing rate is small relative to the parallel effect of small changes in behavior. Still, the effect of time was reduced only modestly when the regression factored out the drift of behavior with time. This suggests that the effect of time was not entirely attributable to changes in behavior. That said, the analysis included only three of the many potentially relevant behavioral parameters. It is almost certainly the case that the apparent effect of time would be reduced further if more behavioral variables (e.g., EMG) or internal variables (satiation/motivation) could be measured. Whether this reduction would be modest or dramatic is difficult to say.
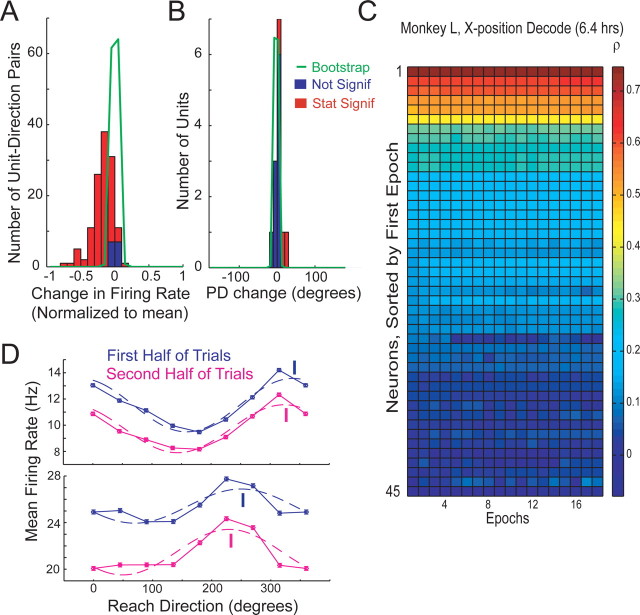
Effects at longer timescales
Monkey L, who generally tends to reach eagerly during experiments, worked for 12,982 successful reaches over 6.4 h during one session. This is our single longest dataset. It offers a unique opportunity to look for neural changes during very long tasks. Figure 3 exhibits the analyses described in Figure 2, which are repeated using this dataset. A significant change in firing rate can be seen in 89.0% of 127 neuron–direction pairs (Fig. 3A) (p < 0.05, FDR corrected). Changes were relatively small with a median absolute change of 14.8% compared with 1.3% in the bootstrap analysis. This is similar to the median value seen in the 1000 reach analysis during the plan periods. However, the overall mean change in firing rate was significantly negative, at −17% (p < 0.05). The decline in firing rate may be attributable to declining motivation across a 6.4 h period. In this dataset, a few small but significant changes in PD are also evident (3 of 13 neurons) (Fig. 3B). Figure 3D shows two of these neurons with both a significant shift in tuning and also a significant decrease in firing rate. The median absolute change was 3.9° compared with 1.5° in the bootstrap analysis. Given the length of this experiment, it seems plausible that these changes result from a change in posture or muscle recruitment: previous results have shown that changes in reach speed (Churchland et al., 2006b; Churchland and Shenoy, 2007) or arm posture (Scott et al., 1997) can significantly alter the preferred direction of a neuron.
Figure 3.
Stability over 6.4 h in monkey L. A, Change in firing rate across 12,982 reaches for all neuron–direction pairs for monkey L between first half and last half of trials, normalized to average rate. B, Shift in preferred direction between first and last half of trials. C, Linear model performance over time for monkey L. D, Example of two neurons with significant shift in PD split into first half (blue) and last half (magenta) of trials. Error bars denote SE. Cosine fits also shown, and PD is denoted by line.
Similarly, for the multiday analyses for monkeys G and H, results are shown in Figure 4. Across days, the median absolute change in firing rate was 30% compared with 5% for the bootstrap analysis. Also, the mean change in firing rate was significantly positive, at 31% (p < 0.05). This positive change may result from selection bias in the datasets. For the main analyses, datasets were chosen in which animals seemed particularly motivated to perform many trials. Therefore, datasets chosen for the multiday analysis may tend to come from less motivated animals. Looking at these individual animals, there was a larger change in firing rate (41%) for monkey H whose data were separated by 1 d than for monkey G (15%) whose data were separated by 2 d. Overall, 79.5% of 88 neuron target pairs show significantly different firing rates (_p_ < 0.05, FDR corrected) (Fig. 4_A_). Across days, there are again small but significant shifts in the PD of 5 of 10 neurons with tuning depth >2 Hz, shown in Figure 4B. Figure 4D shows four examples of tuning curves plotted for 2 d. The largest change is 31° with a target separation of 45° in this task. The median absolute change is 9.9° compared with 2.4° for the bootstrap analysis.
Despite these effects, contributions of individual neurons to linear decoder performance remains relatively stable throughout the long dataset (Fig. 3C) and across days (Fig. 4C) similar to Serruya et al., (2003). Closer inspection of model performance in the long dataset reveals that firing rate changes result in a scaled but similar pattern of activity, which increases the absolute error without strongly affecting the correlation coefficient. The largest change in squared error from a single neuron decoder was 42% across the long dataset and 11% across days. These results are also consistent with previous studies showing a significant decline in open loop decoder performance over time (Wessberg and Nicolelis, 2004; Carmena et al., 2005; Lebedev et al., 2005). However, the relative size of the errors is consistent with a behavioral cause, because the animal's behavior is potentially more similar at the beginning of experiments on different days than after reaching for 6.4 h.
We considered the possibility that recording stability could account for some of the changes observed in long dataset and across days. However, the isolation qualities of the units were evaluated by eye throughout the datasets, and the analyses include only neurons for which stability was independently verified by two observers (see Materials and Methods). Figure 4E shows an example of an electrode containing two units (blue and green) that were matched across days.
Discussion
The central question in this study is whether the relationship between neural activity and behavior is stable or variable over time. That is, if an animal makes highly similar movements, do the properties of the neurons controlling the behavior vary or remain constant? Two experimental techniques allowed us to address this question. First, we are capable of performing stable continuous neural recordings over hours and days with chronic multielectrode arrays. Second, we are capable of tightly controlling our animals' behavior, resulting in reasonably stereotyped movements. Overall, the magnitudes of changes in firing rate and preferred direction were not dramatically larger than those from a bootstrap analysis, as summarized in Table 2. However, several things suggest that there are small but significant changes over time. First, linear decoders tended to show smoothly decaying performance, apparently attributable to changes in mean firing rate. Second, the change in mean firing rate is significantly negative for the 6.4 h analysis and significantly positive for the multiple day analysis. In addition to small kinematic changes, unobserved variables, such as satiation, muscle fatigue, and decreased motivation, may account for these changes (Musallam et al., 2004). Regarding the preferred directions, the median absolute shifts were all smaller than 10°, in a workspace of 360°. Although these values were 2.4–7.5° larger than the shifts for their respective bootstrap distributions, there was no systematic increase in the size of the effects with longer datasets, which is not consistent with a cumulative effect. Rather, this suggests that PD might vary around some intrinsic value (for this task) attributable to noise, subtle changes in behavior, and perhaps plasticity.
These findings corroborate several studies that have found functional stability in neural parameters (Serruya et al., 2003; Greenberg and Wilson, 2004; Musallam et al., 2004) and are consistent with models that assume a stable relationship between motor cortex pyramidal cells and muscle activation (Todorov, 2000). To further consolidate this hypothesis and increase the confidence in identifying neurons across days, it would be desirable to track neural waveforms overnight so their characteristics can be reliably tested over an indefinite time period. Recent advances in autonomous recording devices can be used toward this end (Mavoori et al., 2005; Santhanam et al., 2007).
We designed our study to mimic fairly closely the behavioral task and analysis methods in a study that reported instability in the relationship between neural activity and behavior (Carmena et al., 2005). How can our findings be reconciled with this and other studies that have reported instability? There are at least five possibilities. (1) The relationship between neural activity and behavior may be variable whenever adaptation might occur. (2) The relationship may be variable while an animal is consolidating a new task or switching between tasks. (3) This relationship might appear variable if the task allows for changes in the movement that are still consistent with successful task performance. (4) The relationship might appear variable if there is insufficient data to average out noise. (5) Different brain areas or cortical layers may show different levels of instability.
Consistent with 1, instability during adaptation, this has been documented in cases in which there is active pressure on the system (Li et al., 2001; Paz and Vaadia, 2004). For example, in the study by Padoa-Schioppa et al., (2004), animals often performed force-field adaptation tasks as part of the same experiment. Although data in that study were collected during blocks when no force field was applied, animals might be primed for such changes. Flexibility in the relationship between neural activity and behavior may provide a substrate for rapid adaptation to new environments (Li et al., 2001). Consistent with 2, instability during consolidation of new tasks, monkeys in the study by Carmena et al. (2005) were fairly new to the task. Similarly, in other studies that reported instability (Taylor et al., 2002; Lebedev et al., 2005), the animal switched between manual control and brain control of the on-screen cursor. In our study, there was no pressure to adapt because animals were highly trained on specific tasks.
Consistent with 3, subtle changes in behavior causing apparent instability, all studies have some tolerance for the parameters that define a successful reach. Most studies use manipulanda (Serruya et al., 2003; Padoa-Schioppa et al., 2004; Carmena et al., 2005; Lebedev et al., 2005; Rokni et al., 2007), as opposed to the whole-arm reaches used in our study. Although in both cases only the end point of the hand is monitored, it may be possible to move a manipulandum with a wider range of arm postures and gripping angles. This may be occurring in different ways across different experimental setups and animals. Also, changing the direction of gaze can influence reach-related neurons (Boussaoud et al., 1998; Pesaran et al., 2006; Batista et al., 2007, 2008). In two of our monkeys, eye position was constrained. None of the studies in which variability was reported controlled the eye position. Of course, if the animal changes the actual movement used to achieve task goals, the neural activity associated with that movement will also change, even if the relationship between neural activity and (measured) behavior is stable.
Consistent with 4, the possibility of noise causing perceived nonstationarity in the neuron–behavior relationships, animals in the study by Carmena et al. (2005) reached approximately half as fast as animals in our study, resulting in fewer reaches during the same amount of analyzed neural data. By downsampling our data, we can create instability similar to that observed by Carmena et al. (2005). However, a 5× downsample rather than a 2× downsample is required to qualitatively recreate the variability they observed. Similarly, many of the changes observed by Rokni et al. (2007) might also be attributed to noise. Quantifying the size of PD shifts with the SD of the shift distribution, Rokni et al. (2007) found a change of 19° in the best isolated units. In the most similar analysis presented here, shown in Figure 2B, the SD of the PD shifts was comparable, at 17°. Although small but significant shifts might be important for learning processes, the SD of the corresponding bootstrap distribution was 11°, suggesting that this value is dramatically inflated by the effects of noise. Also, the SD of the differences across days was 16°, which suggests that changes might not increase in size over longer timescales without adaptive pressure to change.
Finally, consistent with 5, different brain areas or cortical layers might exhibit differing degrees of stability and variability. The current study examined the caudal aspect of PMd and the rostral aspect of M1, and instability found was not correlated with position on the electrode array. Previous work showing instability studied neurons recorded in supplementary motor area (Padoa-Schioppa et al., 2004; Carmena et al., 2005) as well as PMd and M1 (Carmena et al., 2005; Rokni et al., 2007). Studies showing a more stable relationship focused on M1 (Serruya et al., 2003), and medial intraparietal area, area 5 and PMd (Musallam et al., 2004). The type and length of the electrodes used may also play an important role. Cortical layers projecting to the spinal cord may exhibit a more stable relationship between neural activity and movements. In the present study, we used an array with electrode lengths (1.0 mm) targeted to record from layer 5. This potentially yielded a larger proportion of corticospinal neurons with a direct relationship to specific muscles (Lemon, 1998) than in other studies.
A few general implications can be drawn from this study. First, the findings of other motor control studies, and perhaps of neurophysiological studies in general, need not necessarily be viewed as time dependent. Data collected across long durations and even multiple days can potentially be combined without much concern that neural tuning may have shifted over the course of the experiment, at least once animals are well trained. Second, this study establishes a stable baseline using several measures on which purposefully induced plastic changes can be reliably detected. Finally, researchers developing brain-machine interfaces can potentially rely on a degree of stability between a patient's intended behaviors and neural activity. Although any neural prosthesis will still need to be adaptable to other changes, such as waveform drift and changing behavioral contexts, this work shows that at least the relationship between neural activity and behavior is reasonably stable on timescales ranging from minutes to a few days.
Footnotes
This work was supported by National Science Foundation Graduate Research Fellowships (C.A.C., B.M.Y., V.G., and G.S.), William R. Hewlett Stanford Graduate Fellowship (C.A.C.), Michael Flynn Stanford Graduate Fellowship (J.P.C), Burroughs Wellcome Fund Career Award in the Biomedical Sciences (A.P.B., K.V.S., and M.M.C.), National Defense Science and Engineering Graduate Fellowships (B.M.Y., V.G., and G.S.), the Christopher Reeve Paralysis Foundation (S.I.R. and K.V.S.), the National Institutes of Health Medical Scientist Training Program (A.A.), Stanford University BioX Fellowship (A.A.), Helen Hay Whitney Foundation Fellowship (M.M.C), and the following awards to K.V.S.: the Stanford Center for Integrated Systems, the National Science Foundation Center for Neuromorphic Systems Engineering at California Institute of Technology, Office of Naval Research, the Sloan Foundation, the Whitaker Foundation, and National Institutes of Health/National Institute of Neurological Disorders and Stroke/Collaborative Research in Computational Neuroscience/Research Project Grant. We thank Mackenzie Risch and Missy Howard for expert surgical assistance and veterinary care, Drew Haven for technical consultation, and Dr. Nicho Hatsopoulos for expert surgical assistance (monkey G implant). We also thank Dr. Jose Carmena for helpful discussion during this project.
References
- Abbott LF, Blum KI. Functional significance of long-term potentiation for sequence learning and prediction. Cereb Cortex. 1996;6:406–416. doi: 10.1093/cercor/6.3.406. [DOI] [PubMed] [Google Scholar]
- Batista AP, Santhanam G, Yu BM, Ryu SI, Afshar A, Shenoy KV. Reference frames for reach planning in macaque dorsal premotor cortex. J Neurophysiol. 2007;98:966–983. doi: 10.1152/jn.00421.2006. [DOI] [PubMed] [Google Scholar]
- Batista AP, Yu BM, Santhanam G, Ryu SI, Afshar A, Shenoy KV. Cortical neural prosthesis performance improves when eye position is monitored. IEEE Trans Neural Syst Rehab Eng. 2008 doi: 10.1109/TNSRE.2007.906958. in press. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc. 1995;57:289–300. [Google Scholar]
- Boussaoud D, Jouffrais C, Bremmer F. Eye position effects on the neuronal activity of dorsal premotor cortex in the macaque monkey. J Neurophysiol. 1998;80:1132–1150. doi: 10.1152/jn.1998.80.3.1132. [DOI] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Henriquez CS, Nicolelis MAL. Stable ensemble performance with single-neuron variability during reaching movements in primates. J Neurosci. 2005;25:10712–10716. doi: 10.1523/JNEUROSCI.2772-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chestek CA, Batista AP, Yu BM, Santhanam G, Ryu SI, Afshar A, Shenoy KV. The relationship between PMd neural activity and reaching behavior is stable in highly trained macaques. Soc Neurosci Abstr. 2006;32:148–5. [Google Scholar]
- Churchland MM, Shenoy KV. Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. J Neurophysiol. 2007;97:4235–4257. doi: 10.1152/jn.00095.2007. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Afshar A, Shenoy KV. A central source of movement variability. Neuron. 2006a;52:1085–1096. doi: 10.1016/j.neuron.2006.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Santhanam G, Shenoy KV. Preparatory activity in premotor and motor cortex reflects the speed of the upcoming reach. J Neurophysiol. 2006b;96:3130–3146. doi: 10.1152/jn.00307.2006. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Ryu SI, Santhanam G, Shenoy KV. Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci. 2006c;26:3697–3712. doi: 10.1523/JNEUROSCI.3762-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci. 1982;2:1527–1537. doi: 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg PA, Wilson AW. Functional stability of dorsolateral prefrontal neurons. J Neurophysiol. 2004;92:1042–1055. doi: 10.1152/jn.00062.2004. [DOI] [PubMed] [Google Scholar]
- Hatsopoulos N, Joshi J, O'Leary JG. Decoding continuous and discrete motor behaviors using motor and premotor cortical ensembles. J Neurophysiol. 2004;92:1165–1174. doi: 10.1152/jn.01245.2003. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Jones KE, Campbell PK, Normann RA. A glass-silicon composite intracortical electrode array. Ann Biomed Eng. 1992;20:423–437. doi: 10.1007/BF02368134. [DOI] [PubMed] [Google Scholar]
- Lebedev MA, Carmena JM, O'Doherty JE, Zacksenhouse M, Henriquez CS, Principe JC, Nicolelis MAL. Cortical ensemble adaptation to represent velocity of an artificial actual controlled by a brain-machine interface. J Neurosci. 2005;25:4681–4693. doi: 10.1523/JNEUROSCI.4088-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemon RN. Pathways and mechanisms subserving cortical control of the hand in primates. Curr Sci. 1998;75:458–463. [Google Scholar]
- Li CS, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- Maass W, Natschlager T, Markram H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. [DOI] [PubMed] [Google Scholar]
- Mavoori J, Jackson A, Diorio C, Fetz E. An autonomous implantable computer for neural recording and stimulation in unrestrained primates. J Neurosci Methods. 2005;148:71–77. doi: 10.1016/j.jneumeth.2005.04.017. [DOI] [PubMed] [Google Scholar]
- Musallam S, Corneil BD, Greger B, Scherberger H, Andersen RA. Cognitive control signals for neural prosthetics. Science. 2004;305:258–262. doi: 10.1126/science.1097938. [DOI] [PubMed] [Google Scholar]
- Nicolelis MAL, Ghazanfar AA, Faggin BM, Votaw S, Oliveira LMO. Reconstructing the engram: simultaneous, multisite, many single neuron recordings. Neuron. 1997;18:529–537. doi: 10.1016/s0896-6273(00)80295-0. [DOI] [PubMed] [Google Scholar]
- Padoa-Schioppa C, Li CS, Bizzi E. Neuronal activity in the supplementary motor area of monkeys adapting to a new dynamic environment. J Neurophysiol. 2004;91:449–473. doi: 10.1152/jn.00876.2002. [DOI] [PubMed] [Google Scholar]
- Paninski L, Fellows MR, Hatsopoulos NG, Donoghue JP. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J Neurophysiol. 2004;91:515–532. doi: 10.1152/jn.00587.2002. [DOI] [PubMed] [Google Scholar]
- Paz R, Vaadia E. Learning-induced improvement in encoding and decoding of specific movement directions by neurons in the primary motor cortex. PLoS Biol. 2004;2:264–274. doi: 10.1371/journal.pbio.0020045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesaran B, Nelson MJ, Andersen RA. Dorsal premotor neurons encode the relative position of the hand, eye, and goal during reach planning. Neuron. 2006;51:125–134. doi: 10.1016/j.neuron.2006.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokni U, Richardson AG, Bizzi E, Seung HS. Motor learning with unstable neural representations. Neuron. 2007;54:653–666. doi: 10.1016/j.neuron.2007.04.030. [DOI] [PubMed] [Google Scholar]
- Sahani M. Computation and neural systems program. Pasadena, CA: California Institute of Technology; 1999. Latent variable models for neural data analysis. [Google Scholar]
- Santhanam G, Sahani M, Ryu SI, Shenoy KV. An extensible infrastructure for fully automated spike sorting during online experiments. the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society; September; San Francisco, CA. 2004. Presented at. [DOI] [PubMed] [Google Scholar]
- Santhanam G, Ryu SI, Yu BM, Afshar A, Shenoy KV. A high-performance brain-computer interface. Nature. 2006;442:195–198. doi: 10.1038/nature04968. [DOI] [PubMed] [Google Scholar]
- Santhanam G, Linderman MD, Gilja V, Afshar A, Ryu SI, Meng TH, Shenoy KV. HermesB: a continuous neural recording system for freely behaving primates. IEEE Trans Biomed Eng. 2007 doi: 10.1109/TBME.2007.895753. in press. [DOI] [PubMed] [Google Scholar]
- Schmidt EM, Bak MJ, McIntosh JS. Long-term chronic recording from cortical neurons. Exp Neurol. 1976;52:496–506. doi: 10.1016/0014-4886(76)90220-x. [DOI] [PubMed] [Google Scholar]
- Scott SH, Sergio LE, Kalaska JF. Reaching movements with similar hand paths but different arm orientations. II. Activity of individual cells in dorsal premotor cortex and parietal area 5. J Neurophysiol. 1997;78:2413–2426. doi: 10.1152/jn.1997.78.5.2413. [DOI] [PubMed] [Google Scholar]
- Serruya M, Hatsopoulos N, Fellows M, Paninski L, Donoghue JP. Robustness of neuroprosthetic decoding algorithms. Biol Cybern. 2003;88:219–228. doi: 10.1007/s00422-002-0374-6. [DOI] [PubMed] [Google Scholar]
- Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Instant neural control of a movement signal. Nature. 2002;416:141–142. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- Simes RJ. An improved Bonferroni procedure for multiple tests of significance. Biometrika. 1986;73:751–754. [Google Scholar]
- Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- Todorov E. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat Neurosci. 2000;3:391–398. doi: 10.1038/73964. [DOI] [PubMed] [Google Scholar]
- Wessberg J, Nicolelis MA. Optimizing a linear algorithm for real-time robotic control using chronic cortical ensemble recordings in monkeys. J Cogn Neurosci. 2004;16:1022–1035. doi: 10.1162/0898929041502652. [DOI] [PubMed] [Google Scholar]
- Williams JC, Rennaker RL, Kipke DR. Long-term neural recording characteristics of wire microelectrode arrays implanted in cerebral cortex. Brain Res Brain Res Protoc. 1999;4:303–313. doi: 10.1016/s1385-299x(99)00034-3. [DOI] [PubMed] [Google Scholar]
- Wise KD, Anderson DJ, Hetke JF, Kipke DR, Najafi K. Wireless implantable microsystems: high-density electronic interfaces to the nervous system. Proc IEEE Inst Electr Electron Eng. 2004;92:76–97. [Google Scholar]
- Yu BM, Kemere C, Santhanam G, Afshar A, Ryu SI, Meng TH, Sahani M, Shenoy KV. Mixture of trajectory models for neural decoding of goal-directed movements. J Neurophysiol. 2007;97:3763–3780. doi: 10.1152/jn.00482.2006. [DOI] [PubMed] [Google Scholar]