Glomerulus-Specific, Long-Latency Activity in the Olfactory Bulb Granule Cell Network (original) (raw)
Abstract
Reliable, stimulus-specific temporal patterns of action potentials have been proposed to encode information in many brain areas, perhaps most notably in the olfactory system. Analysis of such temporal coding has focused almost exclusively on excitatory neurons. Thus, the role of networks of inhibitory interneurons in establishing and maintaining this reliability is unclear. Here we use imaging of population activity in vitro to investigate the mechanisms of temporal pattern generation in mouse olfactory bulb inhibitory interneurons. We show that activity of these interneurons evolves slowly in time but that individual neurons fire at reliable times, with a timescale similar to the slow changes in the patterns of odor-evoked activity and to odor discrimination. Most strikingly, the latency of a single granule cell is highly reliable from trial to trial during repeated stimulation of the same glomerulus, whereas this same cell will have a markedly different latency when a different glomerulus is activated. These data suggest that the timing of granule cell-mediated inhibition in the olfactory bulb is tightly regulated by the source of input and that inhibition may contribute to the generation of reliable temporal patterns of mitral cell activity.
Keywords: olfactory bulb, mitral cell, granule cell, glomerulus, calcium imaging, activation latency
Introduction
The olfactory bulb (and related structures in invertebrates) performs many functions that are remarkably complex, although it is a relatively simple neuronal network (Schoppa and Urban, 2003). The architecture of the olfactory bulb is characterized by reciprocal dendrodendritic synapses between predominantly two cell types: principal cells, mitral/tufted cells, and the local interneurons, granule cells (Rall et al., 1966; Price and Powell, 1970; Jahr and Nicoll, 1980; Shepherd and Greer, 1998). These circuits mediate inhibitory modulation of mitral cell activity (Laurent, 1999; Laurent et al., 2001) and are believed to be critical for refinement of initial odor-evoked mitral cell activity (Yokoi et al., 1995; Friedrich and Laurent, 2001; Luo and Katz, 2001; Shimshek et al., 2005).
Action potential timing is thought to play a key role in coding and computation in the olfactory system. Olfactory stimuli result in reproducible patterns of action potentials lasting tens or hundreds of milliseconds after odor onset (Hamilton and Kauer, 1989; Stopfer and Laurent, 1999; Margrie et al., 2001). Generating such patterns requires reliably timed inhibition, although relatively little is known about the timing of activity of inhibitory interneurons.
Recent work has focused considerable attention on the behavioral and physiological analyses of events that occur between 200 and 800 ms after the onset of odor-evoked activity (Friedrich and Laurent, 2001; Uchida and Mainen, 2003; Abraham et al., 2004; Friedrich et al., 2004). Patterns of odor-evoked activity that are initially highly correlated become progressively more decorrelated over the first several hundred milliseconds after odor stimulation (Friedrich and Laurent, 2001; Stopfer et al., 2003). This decorrelation enhances the discriminability of patterns of mitral cell activity. Evolution of these activity patterns occurs over a time period of hundreds of milliseconds (∼250–800 ms), during which spiking patterns of principle cells (mitral cells and projection neurons) are odor-specific and remarkably reliable trial to trial (Laurent et al., 1996; Wehr and Laurent, 1999; Margrie et al., 2001). Behavioral experiments also have shown that a similar timescale (up to ∼600 ms) is required for rodents to make difficult odor discriminations (Abraham et al., 2004; Rinberg et al., 2006) (also see Uchida and Mainen, 2003). Both time-dependent decorrelation and behavioral discrimination are likely to involve lateral inhibitory interactions between principle cells (Yokoi et al., 1995; MacLeod and Laurent, 1996; Stopfer et al., 1997), most probably mediated by granule cells (Shimshek et al., 2005). Interestingly, lateral inhibition between mitral cells has been shown to have slow rise and decay times (Urban and Sakmann, 2002), reaching peak amplitude in ∼100 ms and having a decay time of ∼350 ms.
The evolution and reliability of such temporal spiking patterns will depend on the inhibitory circuitry of the olfactory bulb. Here we investigate the properties of and mechanisms underlying the slow evolution of dendrodendritic inhibition, focusing on the activity of granule cells. By monitoring the activity of populations of granule cells in vitro, we find that granule cells fire with long but reliable latencies after stimulation of single mitral cells or populations of mitral cells. Although latencies ranged widely across cells, latencies of single granule cells were input specific, thus linking the timing of inhibitory modulation of mitral cell activity to odor identity.
Materials and Methods
Slice preparation
Slices were prepared using methods adapted from previous work (Urban, 2002). Mice (2–3 weeks old, C57BL/6) were deeply anesthetized with a mixture of 0.1% ketamine and 0.1% xylazine (∼100 μl dose, monitored by responsiveness to tail pinch) and then decapitated. Brains were removed and placed in ice-cold Ringer's solution (in mm: 125 NaCl, 25 glucose, 2.5 KCl, 25 NaHCO3, 1.25 NaH2PO4, 1 MgCl2, and 2.5 CaCl2). Sagittal or coronal slices (300 μm thick) of olfactory bulbs were cut using a vibratome (VT1000S; Leica, Nussloch, Germany). After cutting, slices were incubated in the above Ringer's solution (continuously oxygenated) at 37°C for 30 min before being loaded with calcium dye.
Electrophysiology
Whole-cell recordings were made using patch pipettes filled with internal buffer (130 mm potassium gluconate, 10 mm HEPES, 2 mm MgCl2, 2 mm MgATP, 2 mm Na2ATP, 0.3 mm GTP, 4 mm NaCl, and, in some cases, 1% biocytin), using a Multiclamp 700A amplifier (Molecular Devices, Palo Alto, CA) and ITC-18 data acquisition board (InstruTech, Port Washington, NY). Cells were visualized under infrared differential interference contrast (DIC) optics (BX51WI; Olympus Optical, Tokyo, Japan). Physiological data were collected via software written in Igor Pro (WaveMetrics, Lake Oswego, OR). Depending on the type of cells, appropriate whole-cell patch pipettes (1–3 MΩ for mitral cells and 5–10 MΩ for granule cells) were used to make current-clamp recordings. Extracellular stimulation was delivered via theta glass electrodes pulled to a tip size of ∼1 μm using a single constant-current pulse (300 μs). All of the experiments were done at 35°C in modified Ringer's solution (in mm: 125 NaCl, 25 glucose, 2.5 KCl, 25 NaHCO3, 1.25 NaH2PO4, 0.2 MgCl2, 2.5 CaCl2) unless stated otherwise.
Fura-2/fura-4F AM loading
Olfactory bulb slices were transferred to a special chamber containing 500 μl of Ringer's solution in which they were loaded with membrane-permeable calcium indicators using methods adapted from previous work in cortical slices. Humidified air was passed above the surface of liquid in the chamber to keep the solution oxygenated. To the incubation chamber, we added 3 μl of 0.01% pluronic (Invitrogen, Carlsbad, CA) and 5 μl of a 1 mm solution of either fura-2 or fura-4F AM (Invitrogen) in 100% DMSO solution Slices were incubated in this solution at 37°C for 60–90 min. Data reported here were collected with fura-2-loaded slices unless stated otherwise. After tissue loading, the tissue is much more fluorescent than control tissue, suggesting that considerable dye is contained in neuropil structures that are not individually identifiable (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). However, under our conditions, the neuropil staining does not show stimulus-evoked changes in fluorescence, as indicated in supplemental Figure 3 (available at www.jneurosci.org as supplemental material).
Imaging
After loading, slices were placed in a submersion recording chamber under an upright microscope using 20, 40, or 60× water immersion objectives (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). For a particular experiment, an objective was chosen to give the best tradeoff between field of view (330 vs 165 vs 110 μm) and brightness of the image (numerical aperture of 0.5, 0.8 or 0.9). Slices were visualized for successful loading using excitation wavelength of 360–400 nm and emission wavelength of 480–520 nm. Experiments were performed at 37°C unless stated otherwise. A cooled back-illuminated frame transfer CCD camera (Micromax 512 BFT; Princeton Instruments, Trenton, NJ) was used to capture single fluorescent images and sequences of images (movies). Exposure times were 30–60 ms per frame with 3 × 3 binning (final image size, 170 × 170 pixels). Images were acquired and stored using software written in Igor Pro (WaveMetrics) using drivers (SIDX) from Bruxton Scientific (Seattle, WA).
After loading, extracellular stimulation elicited decreases in fluorescence in many imaged neurons. In response to a given stimulus, only a fraction of the cells visibly labeled in the raw fluorescence image showed calcium transients. To investigate the response profile of granule cells, we acquired 2-s-long movies (30–60 ms/frame) of the granule cell layer in fura-2-loaded slices after glomerular stimulation (300 μs constant-current pulse). Movies were analyzed by calculating Δ_F_/F frame by frame for whole movies and then identifying cells showing decreases of fluorescence across the frames of individual movies. The response profiles of different granule cells were plotted as Δ_F_/F (change in fluorescence/basal fluorescence) versus time by calculating the change in average pixel values over a particular region of interest. We chose not to perform background subtraction before calculating Δ_F_/F because identifying a background region in which fura fluorescence did not contribute to the total signal was not possible. This presumably reflects the fact that calcium dye is distributed in the cytoplasm of cell bodies and neuronal processes throughout the thickness of the slice.
Data analysis
The response profiles of different granule cells were plotted as Δ_F_/F (change in fluorescence/basal fluorescence) versus time by calculating the change in average pixel values over a particular region of interest. These regions of interest were the size of single granule cells and, in many cases, were identifiable as single cells in either fluorescence or the DIC image. Activation latency was calculated as the time of first deviation from the basal florescence, and rise time was the difference between the time of first deviation and time taken to attain the peak florescence. We used the total rise time of granule cell calcium transients as a measure of total duration of granule cell activity.
Probability.
Probability of a single cell was defined as the ratio of number of trials on which a given cell showed any measurable activity to the total number of trials (experiments in which a minimum of 10 trials was performed were used to calculate this probability). The probability index was calculated as mean of probability of all of the cells imaged for a given condition.
For IPSC reliability analysis, we used custom mini-analysis software to detect IPSCs and then convolved these train of events with a square function of width 50 ms. These convolved trials were used to calculate the pairwise cross-correlation across trials.
The correlogram computed from these data were compared with the same computed from simulated trials. To generate simulated IPSC trains, we computed the average rate of events for all trials (50 trials). New simulated spike trains were generated randomly from this measured time-dependent frequency of events.
Analysis.
For clustering trials based on response latency vectors or binary activity vectors, we calculated the distance between a vector representing a given trial and a vector that was the ideal vector (defined below) for all of the trials on which a given glomerulus was stimulated. Specifically, dij = [vector]Gi × [vector]gj − [vector]gj × [vector]gj, where [vector]Gi is ideal response vector for _i_th glomerulus (i = 1 or 2). [vector]gj is trial vector for _j_th trial (j = 1–20, 10 trials each for two glomeruli). For clustering analysis based on latencies, [vector]Gi is the vector of mean response latencies for granule cells (for all trials on which the cell was activated). For clustering analysis based on binary activity, [vector]Gi is a vector giving the reliabilities of granule cell activity in response to stimulation of a given glomerulus. After computing the distance a trial was from the two ideal vectors, we plotted each trial in two dimensions to generate Figure 7, G and H.
Figure 7.
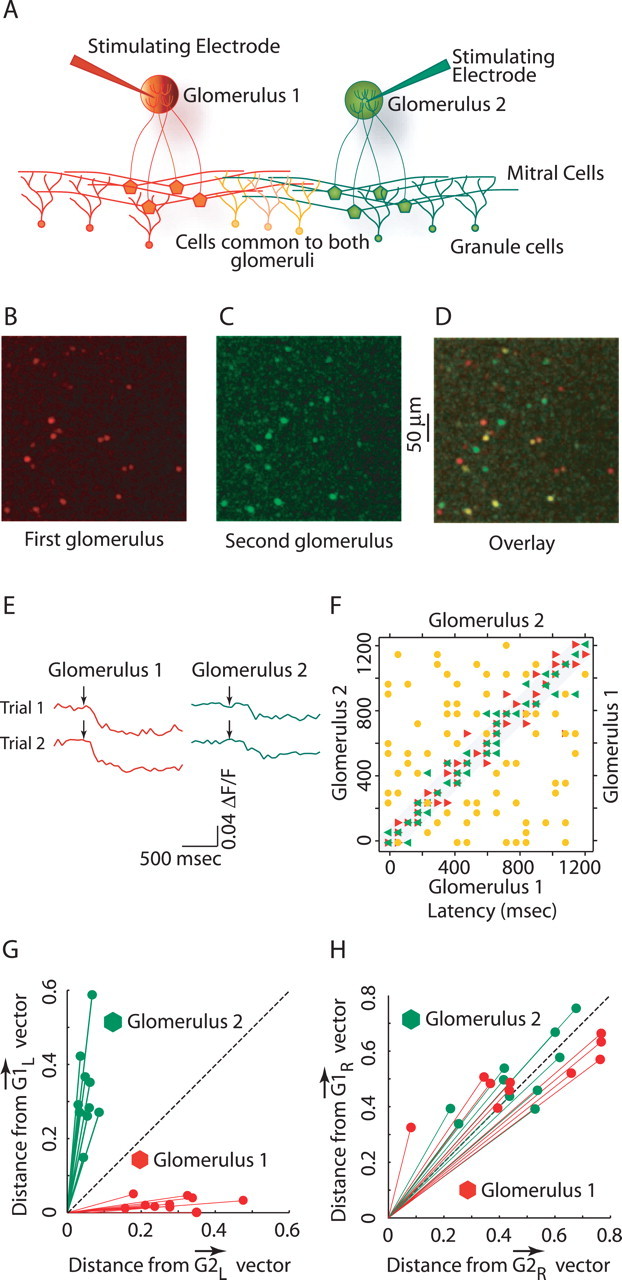
Glomerulus specificity of granule cell activation latencies. A, Experimental setup showing stimulation of two glomeruli that activates overlapping populations of granule cells. B, C, Activity evoked by first (red) and second (green) glomerular stimulation, respectively. D, Overlay of B and C, showing the overlap in activity evoked by two glomeruli. Yellow cells are activated by both the glomeruli. E, Calcium transients from a single granule cell active in D. Traces show calcium transients in response to stimuli of one glomerulus (red) and the other glomerulus (green). Note that latencies of same-colored traces are the same but different for transients elicited by stimulation of different glomeruli. F, Plot showing the latencies for the overlapping set of granule cells (as the yellow cells in D above; n = 68), for two stimuli of the same (shown in red and green triangles) and for two different glomeruli (shown in yellow circles). G, Projections of trial vectors (vectors containing the latency information of granule cells) onto the ideal response vectors for two glomeruli (_[vector]G_1l and _[vector]G_2l), showing glomerulus-specific clustering of trials. H, Projections of trial vectors (vectors contains information only about the activity state of granule cells) on the ideal response vectors for two glomeruli (_[vector]G_1r and _[vector]G_1r).
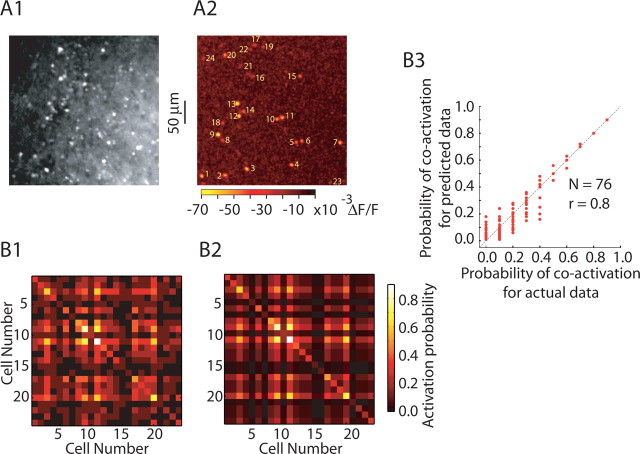
To calculate the correlation matrix in Figure 8, the activation probability of a single cell was calculated as the proportion of the total trial activity shown by that cell. Pairwise coactivation probability (data) was defined as the ratio of number of trials both the cells showed activity to the total number of trials. For predicted coactivation probability, activation probabilities of cells were considered as independent events and pairwise coactivation probability was calculated as the product of activation probabilities of individual cells.
Figure 8.
Granule cell activity is uncorrelated. A1, Raw fluorescence image of fura-2-loaded olfactory bulb slice. A2, Union of 10 successive trials of granule cell population activity in response to glomerular stimulation, showing a total of 24 granule cells active during these trials. B1, B2, Correlation matrices for activity of cells shown in A2. B1, Actual data show the probability (of ≥10 trials) of each of the 24 granule cells firing on a given sweep (diagonal) and the probability of pairs of cells being both activated (nondiagonal elements). B2, Like B1, except that the values give the correlation predicted by chance, assuming cells are active independently. Similarity between B1 and B2 indicates that cells are actually independent, i.e., that activity across a population of granule cells is uncorrelated. B3, Summary plot showing strong correlation between predicted coactivation probability (as B2) and actual coactivation probability (as in B1).
Statistical analysis.
Wilcoxon's rank sum test was used to compare the distributions unless stated otherwise.
Results
Granule cells show asynchronous and repetitive firing after glomerular stimulation
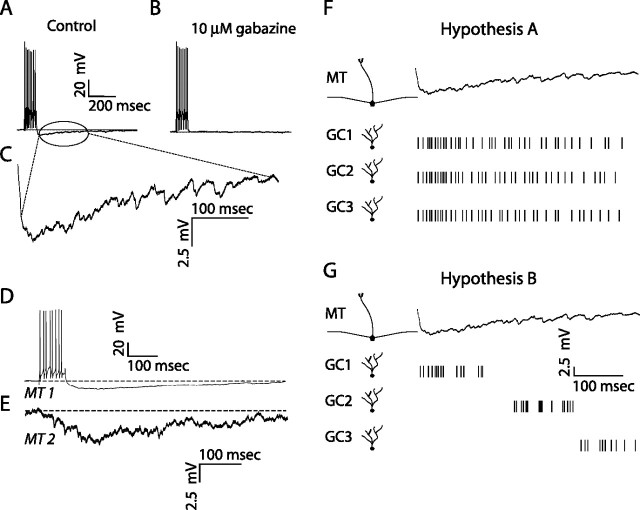
The kinetics of recurrent and lateral inhibition are quite slow (Fig. 1A–E), with 350 ms decay times being typical (Isaacson and Strowbridge, 1998; Schoppa et al., 1998; Margrie et al., 2001; Urban and Sakmann, 2002). These slow kinetics arise because recurrent and lateral inhibition consist of asynchronous barrages of fast GABAA receptor-mediated IPSCs (Fig. 1C), presumably resulting from release of GABA from many different granule cells. Two possible mechanisms for the asynchrony of this granule cell-mediated inhibition are (1) rapid recruitment and persistent activity of granule cells (Fig. 1F), or (2) asynchronous recruitment of a number of granule cells (Fig. 1G). These two hypotheses are not mutually exclusive, but they have different implications in olfactory information processing. To investigate these hypotheses, we monitored activity of populations of granule cells in olfactory bulb slices using bulk-loaded calcium indicators using methods similar to those previously applied in other preparations (Peterlin et al., 2000; Ikegaya et al., 2004).
Figure 1.
Kinetics of recurrent and lateral IPSPs. A, Mitral cell voltage trace in response to current injection (300 pA for 100 ms) showing a series of spikes, followed by long-lasting recurrent inhibition. B, Same mitral cell voltage response to current injection after the addition of 10 μm gabazine to the bath. C, Enlarged view of mitral cell voltage trace showing the presence of many high-frequency inhibitory synaptic events. D, E, Mitral cell (MT) voltage traces for two mitral cells (bottom trace is an average), in response to current injection (400 pA for 100 ms) in cell 1, showing the time course of inhibition (lateral) in the second cell. F, G, Hypotheses to explain the duration of recurrent and lateral IPSPs. F, Hypothesis A: single granule cells are persistently active. After a single stimulus, individual granule cells maintain activity with a time course comparable with that of recurrent (or lateral) inhibition. G, Hypothesis B: granule cell latencies are widely distributed. Different granule cells have different activation latencies that are randomly distributed along the time course of dendrodendritic (recurrent/lateral) inhibition.
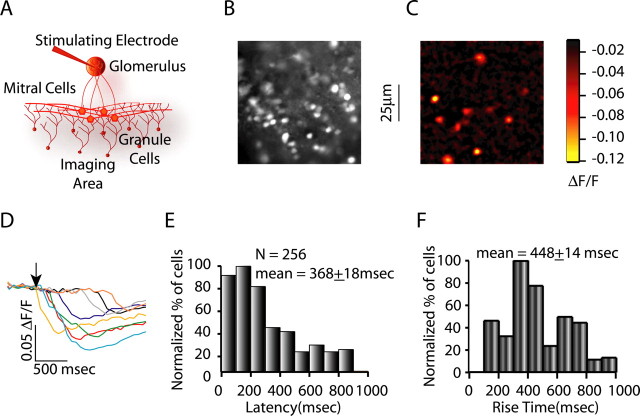
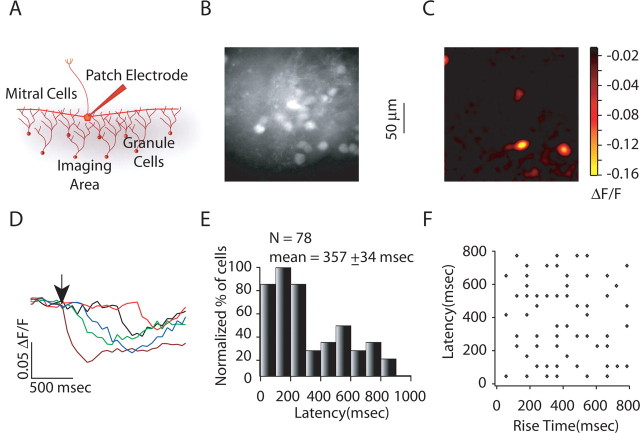
In initial experiments, we found that we could image calcium transients in granule cells after extracellular stimulation in the glomerular layer, a manipulation that generates lateral inhibition via mitral cell firing and subsequent granule cell activity. Extracellular stimulation (single 0.01–1.0 mA pulses of 100–300 μs duration) in the glomerular layer resulted in calcium transients being recorded in 10–25 granule cells per stimulus (Fig. 2A–C). By combining calcium imaging in bulk-loaded slices and cell-attached recording, we simultaneously monitored spiking and calcium transients in granule cells to determine the physiological correlate of the calcium transients. Using this approach, we determined that calcium transients corresponded to action potentials, with the rising phase of the transient corresponding to periods of repetitive firing (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). As shown in Figure 2, D and E, we found that the latency of granule cell calcium transients after stimulation of the glomerular layer ranged widely, from 0 to 900 ms, with a mean of 368 ± 18 ms (n = 256 granule cells). We also quantified the rise times of granule cell calcium transients after glomerular stimulation to get an indication of the duration of granule cell spiking. The rise times of granule cell calcium transients were also widely distributed (mean of 448 ± 14 ms; n = 256) (Fig. 2F). These results demonstrate asynchronous and long-latency recruitment of granule cells after activation of populations of mitral cells. Additionally, activity of individual granule cells persists for hundreds of milliseconds after their initial activation, as indicated by the long rise times of the calcium transients. We did not analyze the spatial patterns of granule cell activity, in part because of concerns that these patterns would be influenced by slice angle and other biologically uninteresting details of the experiment. However, we typically found the maximum density of activated granule cells in the superficial granule cell layer directed beneath the stimulated glomerulus.
Figure 2.
Response latencies and durations of granule cell activity for glomerular stimulation. A, Experimental setup for recording granule cell calcium transients in response to glomerular stimulation. B, C, Raw fluorescence and glomerular stimulation-evoked activity in the granule cells, respectively. D, Granule cell calcium transients for cells shown in C in response to glomerular stimulation. The arrow depicts the time of stimulation. E, Granule cell activation latency histogram for glomerular stimulation (average latency, 368 ± 18 ms; n = 256), showing widely distributed activation latencies. F, Granule cell rise time histograms for glomerular stimulation (average, 448 ± 14 ms), showing widespread distribution of granule cell rise times.
We investigated possible mechanisms underlying the unusually slow patterns of granule cell activity elicited by glomerular stimulation. We first asked whether our stimulation resulted in asynchronous activation of mitral cells, which then generated asynchronous granule cell activity. To test this hypothesis, we examined the distribution of mitral cell activation latencies in response to glomerular stimulation (Fig. 3A–C). We found that the majority (∼98%; n = 38) of the mitral cells showed calcium transients that were visible in the first frame recorded after the stimulus (30–60 ms frame rate) (Fig. 3B,C). Thus, the wide distribution of granule cell activation latencies is not a result of long latencies of mitral cell firing.
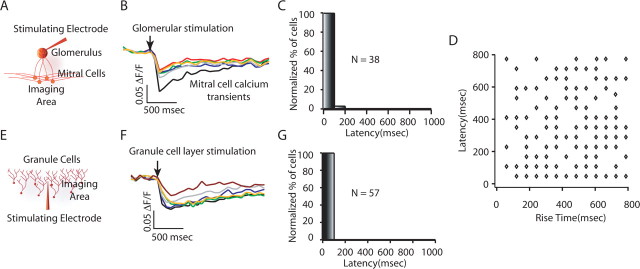
Figure 3.
Possible sources of long-latency granule cell spiking. A, Experimental setup for imaging mitral cell activity in response to glomerular stimulation. B, C, Mitral cell calcium transients (B) and mitral cell response latency histogram in response to glomerular stimulation (C), showing near simultaneous activation of mitral cells. The arrow depicts the time of glomerular stimulation. D, Plot of granule cell response latencies versus granule cell rise time for glomerular stimulation. There was no correlation between granule cell activation latencies and granule cells rise times (r = 0.13). E, Experimental setup for imaging granule cell activity in response to extracellular stimulation in the granule cell layer. F, G, Granule cell calcium transients (F) and granule cell response latency histogram in response to granule cell layer stimulation (G), showing low variability in the granule cell responses.
Next, we examined the granule cell latencies in response to direct stimulation of the granule cell layer to determine whether the kinetics of granule cell activity were attributable to intrinsic excitability of granule cells or whether they were a specific consequence of activation of granule cells by mitral cells (Fig. 3E–G). Extracellular stimulation in granule cell layer, which should result in direct activation of granule cells and also activation by ascending axons, caused granule cell activity with short latencies and rise times (100% of these cells were active in the first frame after the stimulation, with average rise times of 152 ± 17 ms; n = 57) (Fig. 3E,F). This indicates that the long-latency granule cell responses observed above are not attributable to intrinsic kinetics of granule cell firing or to our method of measuring activation time and duration, but rather are a feature of granule cell activation by mitral cells.
Given the large ranges in the latency to granule cell activity and duration of this activity, we wondered whether short-latency events also had long rise times. Such a relationship would suggest that the long-latency events occur preferentially in weakly activated granule cells, which should also produce only a few action potentials and thus short rise times. In fact, we found no relationship between response latency and response rise time (Fig. 3D) (r = 0.13). This suggests that the long latency and the long duration of the granule cell responses are generated by different mechanisms and indicates that the long-latency responses are unlikely to be caused simply by low levels of input. We considered examining the relationship between latency and amplitude of calcium transients, but cell-to-cell differences in dye concentration in bulk-loaded tissue would influence the amplitude of calcium transients, making interpretation of amplitude data suspect.
Asynchronous activation of granule cells after stimulation of single mitral cells
We next measured granule cell activity after stimulation of single mitral cells by whole-cell current injection (Fig. 4A). Activation of single mitral cells (8–10 spikes at 100 Hz) resulted in calcium transients being recorded in three to five granule cells (Fig. 4B,C). This form of stimulation resulted in widely distributed granule cell response latencies (Fig. 4D,E) (mean of 357 ± 34 ms; n = 78) and rise times (data not shown) that did not differ significantly from those seen with extracellular stimulation (p > 0.5 for Wilcoxon's rank sum test). Furthermore, as with extracellular stimulation of single glomeruli, latencies of granule cell activity and the duration of their activity showed no correlation (Fig. 4F) (r = 0.22), suggesting that strength of input was not related to short-latency events. These two results confirmed the finding that long-latency responses can be attributed to granule cell activation by mitral cells and shows that the slow kinetics of recurrent and not just lateral inhibition are attributable to asynchronous activation of granule cells.
Figure 4.
Response latencies and duration of granule cell activity for single mitral cell stimulation. A, Experimental setup for imaging granule cell activity in response to single mitral cell stimulation. B, C, Raw fluorescence and Δ_F_/F image showing single mitral cell stimulation-evoked activity, respectively. D, Granule cell calcium transients for cells shown in C. The arrow depicts the time of stimulation. E, Granule cell activation latency histogram for glomerular stimulation (average latency, 357 ± 34 ms; n = 78), showing widely distributed activation latencies. F, Plot of granule cell response latencies versus granule cell rise time for glomerular stimulation. There was no correlation between granule cells activation latencies and granule cells rise time (r = 0.22).
Asynchrony of granule cell activation can be reduced by blockade of A-type potassium channels
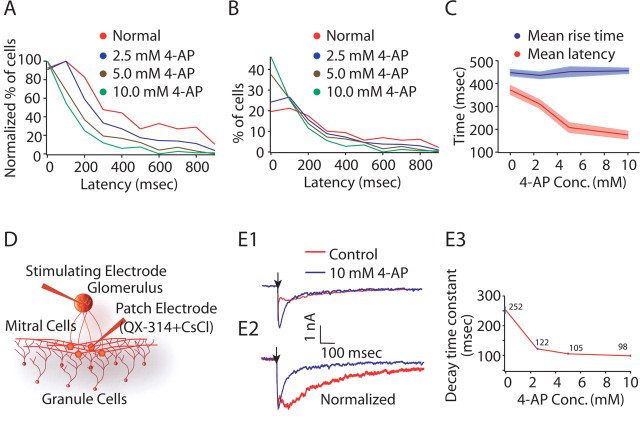
We next investigated how this asynchronous activity is generated across a population of granule cells and whether the differences in latencies across granule cells are attributable to different intrinsic properties of the granule cells. Previous work (Schoppa and Westbrook, 1999) has shown that granule cells express a high density of A-type potassium channels, which are believed to be important for generating delayed firing. Thus, it is possible that different granule cells express different amounts of A-current and thus have different latencies. If this is true, then blockade of A-current should reduce long-latency events and increase the degree to which granule cells fire synchronously. Thus, we used fura imaging to record granule cell activity after glomerular stimulation under different concentrations of the A-current blocker 4-aminopyridine (4-AP). Blockade of A-current resulted in a marked shift in the distribution of granule cell latencies (Fig. 5A–C). The mean response latency shifted from 368 ± 18 ms (normal conditions; n = 256) to 182 ± 16 ms for 10 mm 4-AP (n = 182; p < 0.01 for Wilcoxon's rank sum test). [Mean response latencies were 310 ± 17 ms for 2.5 mm 4-AP (n = 242) and 213 ± 20 ms for 5 mm 4-AP (n = 109).] Because granule cell latencies were more homogeneous when A-current was blocked, this suggests that the slow time course of granule cell-mediated inhibition can be attributed in part to the differential activation of _I_A in a population of granule cells, attributable to either differential expression of A-channels (somatically or in the dendrites) or differences in how the inputs they receive activate A-current. The reduction in latencies was most pronounced at high 4-AP concentrations, suggesting that it is attributable to blockade of A-current mediated by Kv4.X-type channels because the affinity of 4-AP for these channels is in the millimolar range (Barish, 1986). In the olfactory bulb, these channels are expressed predominantly by granule cells and periglomerular cells rather than in mitral cells (Serodio and Rudy, 1998). Other transient potassium currents (such as the D-current, expressed by mitral cells) are blocked by much lower concentrations of 4-AP (nanomolar range) (Balu et al., 2004).
Figure 5.
Blockade of transient potassium channels alter granule cell latencies. A, Granule cell activation latency distributions: red, normal conditions (average latency, 368 ± 18 ms; n = 256); blue, 2.5 mm 4-AP (average, 310 ± 17 ms; n = 242); brown, 5.0 mm 4-AP (average, 213 ± 20 ms; n = 108); green, 10.0 mm 4-AP (average, 182 ± 16 ms; n = 149), showing shift in granule cell activation latency distribution after blocking _I_A. Curves have been normalized to the peak of the curves. B, Granule cell activation latency distributions for conditions described in A. Curves have been normalized to the area under curves. C, Plot for average rise times and average latencies under different concentrations of 4-AP showing no significant difference in the total rise time of granule cell calcium transients under different conditions (mean rise time was 448 ± 14 ms for normal condition, 423 ± 15 ms for 2.5 mm 4-AP, 452 ± 22 ms for 5 mm 4-AP, and 456 ± 19 for 10 mm 4-AP) (p > 0.1 for Wilcoxon's rank sum test). D, Experimental setup for measuring decay time constant of granule cell-mediated inhibition. E1, E2, 4-AP resulted in faster granule cell-mediated inhibition and reduced the time-to-peak of inhibition. The arrow depicts the stimulation time. E3, 4-AP reduced the decay time constant of granule cell-mediated inhibition. QX-314, 2(Triethylamino)-_N_-(2,6-dimethylphenyl) acetamine.
We also analyzed the effects of different 4-AP concentrations on the duration of granule cell activity (Fig. 5C). We found little difference in the total duration of granule cell activity under different conditions (mean rise time was 423 ± 15 ms for 2.5 mm 4-AP, 448 ± 22 ms for 5 mm 4-AP, and 462 ± 19 for 10 mm 4-AP) (p > 0.1 for Wilcoxon's rank sum test). This suggests that, although blocking of _I_A reduced the variability in granule cell latencies, it did not strongly affect the total activity of single granule cells. Furthermore, granule cell-mediated inhibition evoked by extracellular stimulation of the glomerular layer showed significantly faster kinetics (Fig. 5E1–E3) with application of 4-AP [decay time constant, 252 ± 13 ms for control (n = 5) vs 105 ± 2 ms for 5 mm 4-AP (n = 5) with p < 0.01 for Wilcoxon's rank sum test]. With blockade of _I_A, this GC-mediated inhibition (n = 8) peaks earlier (Fig. 5E1,E2) and the peak amplitude is higher than that under control conditions (256 ± 28%). This favors the possibility of _I_A-induced variability in a population of granule cell that results in asynchronous activation of a population of granule cells and thus the ensuing slow kinetics of dendrodendritic inhibition. Although blocking of _I_A resulted in lower divergence in populations of granule cells, it did not totally eliminate the heterogeneity in the responses of different granule cells, suggesting that other mechanisms also contribute to long-latency spiking of granule cells.
Granule cells are activated with low probability but with reliable timing
In initial experiments, we observed that granule cells were activated at relatively low probability across trials. To determine the probability with which granule cells were activated, we imaged the activity of a population of granule cells in response to glomerular stimulation for large numbers of trials (≥10 with intertrial interval of approximately 20 s). As shown in Figure 6, A1 and A2, granule cells were activated with relatively low probability (granule cells responded in only 25 ± 4% of the total recorded trials; n = 46). Despite this low probability of firing, when granule cells responded, the amplitude and latency of their calcium transients were remarkably reliable across trials (Fig. 6A2). The mean SD for granule cell latencies across trials was 60.6 ms (Fig. 6C) (n = 24). We further investigated whether blocking A-current altered the probability of granule cell activity. Application of 10 mm 4-AP resulted in a marked increase in the probability of granule cell firing across trials (30 ± 4% for 2.5 mm 4-AP, 49 ± 5% for 5 mm 4-AP, and 58 ± 6% for 10 mm 4-AP; n = 79) (Fig. 6B1–B3). Application of 4-AP did not seem to affect the trial-to-trial reliability of activation latencies (Fig. 6B2).
Figure 6.
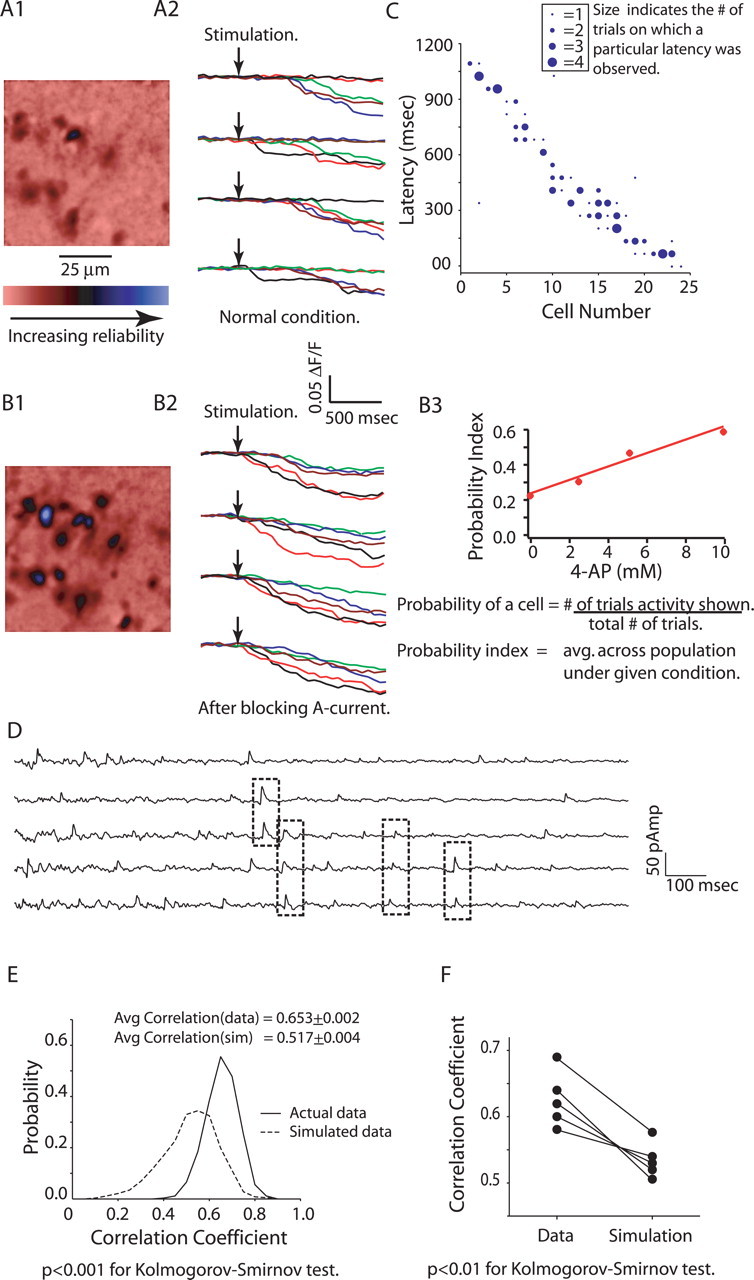
Granule cell activation has low probability but high reliability. A1, B1, Averages of Δ_F_/F map for 10 trials each for granule cell population activity in response to glomerular stimulation under normal conditions (A1) and 10 mm 4-AP (B1), showing low probability of granule cell activation for glomerular stimulation. A2, B2, Calcium transients for four successive trials for five of the cells shown in A1, under normal conditions (A2) and for 10 mm 4-AP (B2). The probability of granule cell activation is low but activation latencies are reliable trial to trial. B3. Blocking of A-current by 4-AP increases the reliability of granule cells. C, Plot showing the reliability in granule cell latencies (24 randomly chosen cells to depict the entire range of activation latencies). D, Current recordings (5 selected) from a mitral cell (voltage clamped at −40 mV) in response to glomerular stimulation showing IPSCs with same latencies across trials. E, Histogram showing pairwise correlation for 50 consecutive current recordings from a mitral cell (solid line) and the same for 50 simulated trials (dotted line), showing higher correlation for IPSCs across trials than expected by chance. F, Plot showing higher average correlation for IPSCs recorded in five different mitral cells than the simulated trials.
Granule cell-mediated IPSCs show reliable latencies
The observation that granule cells fire with latencies that are reliable to within 60 ms suggests that granule cell-mediated inhibition also should be temporally reliable at a similar timescale. To investigate the reliable timing of inhibition observed in mitral cells, we recorded IPSCs from mitral cells (voltage clamped at −40 mV) in response to repeated stimulation (50 sweeps) of a single glomerulus (Fig. 6D). To determine whether some IPSCs occurred at consistent latencies, we first identified the time of IPSC peaks and then convolved these trains of events with a square function of width 50 ms. This convolution means that the data on IPSC timing were effectively binned with 50 ms bins, allowing us to use the same sampling rate for both imaging and patch-clamp data. We then calculated the pairwise correlation coefficients for these binned data for the group of 50 trials. These sweeps showed a relatively high average correlation coefficient (0.65 ± 0.002) (Fig. 6E). To determine whether the computed cross-correlation is different from that observed by chance, we compared this value with the same value computed from simulated event trains having the same bin-by-bin time-dependent frequency of events (for details, see Materials and Methods) (Fig. 6E). We observed significantly higher correlation for IPSCs recorded from the mitral cells than for the simulated events (0.63 ± 0.02 for actual events vs 0.55 ± 0.02 for simulated events; n = 5 cells; p < 0.01 for Kolmogorov–Smirnov test) (Fig. 6F). This indicates that some IPSCs occur reliably (to within 50 ms) at fixed times after the stimulation across many trials, consistent with our data from imaging granule cell activity. Higher precision reliability was not evaluated in these experiments.
Granule cell latencies are reliable and glomerulus specific
Odor-evoked mitral cell firing often consists of periods of increases and decreases in firing rate that occur over hundreds of milliseconds. In many cases, these complex patterns are odor specific and are reliably evoked across repeated presentations of the same odor (Friedrich and Laurent, 2001). Blockade of inhibition alters the patterns of odor-evoked firing in mitral cells (Yokoi et al., 1995; Margrie et al., 2001) and in their insect analogs (Stopfer et al., 1997), and thus it seems likely that dendrodendritic inhibition plays a role in generating these odor-specific firing patterns. We tested whether the latency and/or kinetics of granule cell activity in our experiments is reliable across repeated stimulation of the same glomerulus and whether these features of the response of single granule cells are different when a single granule cell is activated by stimulation of different glomeruli.
We examined the latencies to initial activity across populations of granule cells after extracellular stimulation in neighboring pairs of glomeruli (Fig. 7A). When neighboring glomeruli were stimulated, we saw 15–30% overlap in the populations of active granule cells. For this subset of granule cells, we then compared the latencies of calcium transients after stimulation of the different glomeruli and also after repeated stimulation in the same glomerulus (Fig. 7E,F). Latencies of single granule cells differed when two different glomeruli were stimulated (Fig. 7F, yellow circles) (Wilcoxon's rank sum test; p ≤ 0.01), whereas, consistent with the data above, latencies for single granule cells were very similar when a single glomerulus was stimulated repeatedly (p > 0.5 for Wilcoxon's rank sum test) (Fig. 7F, red and green triangles). We calculated the difference in latencies for granule cells in response to glomerular stimulation for two consecutive trials and in response to stimulation of two different glomeruli, and these differed significantly. This finding shows that granule cell activation latencies are glomerulus specific, which in turn suggests that granule cell latencies may effectively code which glomeruli are active. To test whether latency data were sufficient to determine which glomerulus was stimulated, we represented each trial as a vector (of length 12), in which each element represented the latency of one granule cell (20 trials, 10 each for two different glomeruli; inter-trial interval was ≥20 s). We then projected each trial vector on to ideal response vectors (_[vector]G_1l and _[vector]G_2l; see Materials and Methods) for both glomeruli. This projection analysis was used as a way of depicting the similarity of trials in the plane. We observed a clear glomerulus-specific clustering of trials and distinct separation of the trials depending on which glomerulus was stimulated (Fig. 7G). Hence, the latencies of granule cell activity provide sufficient information to identify the activated glomerulus. We repeated the same analysis to determine whether the identity of activated granule cells (within the set of cells that could be activated by both glomeruli) could be used to determine which glomerulus was stimulated. In this case, trial vectors represented only the activity state of granule cells on a given trial (1 if granule cell was active and 0 if granule cell was inactive). Each of these trials was then projected on to ideal response vectors (_[vector]G_1r and _[vector]G_2r; see Materials and Methods). These projections were not clustered, and, thus, within the subset of cells activated by stimulation of either glomerulus, the identity of the activated cells on a given trial did not provide information sufficient to identify the active glomerulus (Fig. 7H).
Granule cell activity is uncorrelated across the population and across trials
We next investigated the degree to which activity of granule cells was correlated both within and across trials. Specifically, we wanted to determine whether subsets of granule cells were coactive more often than predicted by their individual response probabilities (within trial correlation) and whether the probability of granule cell firing varied in a consistent manner from trial to trial (across trial correlation). We recorded the activity of populations of granule cells (Fig. 8A1,A2) in response to glomerular stimulation for at least 10 trials (intertrial intervals of ∼20 s). We first calculated the probability of firing for each cell across all the trials and we used these probabilities to predict the joint probability that these cells would be coactive (assuming that their activities were independent of each other). These results were displayed as a matrix in which the value at each point (row, column) shows the probability that the cells in the given row and column are both activated (Fig. 8, data in B1 and predicted coactivation probabilities in B2). Thus, the diagonal elements give the probability of firing for each cell. If the activity of these granule cells is pairwise independent, then the predicted value of the off-diagonal elements can be determined by multiplying the probabilities of activity for the cells in the given row and column. In Figure 8, as summarized in B3 and evident from B1 and B2, actual and predicted coactivation probabilities were highly correlated (r = 0.8 for n = 76 cells). This implies that the coactivation observed is consistent with the assumption that individual granule cells are activated independently. The only potential deviation from independence was found in looking at activity of the cells with the lowest probability of being activated. In this case, the probability of rarely active cells being coactive was somewhat higher than predicted by chance.
Discussion
Dendrodendritic inhibition in the mammalian olfactory bulb is critical for regulating both the frequency and timing of mitral cell spiking, yet many features of this phenomenon and the mechanisms that generate them are not well understood. Here we analyzed the activity of ensembles of granule cells after mitral cell activity using population imaging after bulk loading of calcium indicator. We show that granule cell population activity consists of spiking at widely ranging latencies (0–1000 ms), that these latencies are reliable across trials, and that the latencies are specific to stimulation of particular glomeruli. The duration of granule cells activity was independent of granule cell activation latencies, suggesting that longer latencies cannot be explained simply as being attributable to less input to the granule cells. These data indicate that glutamate release from mitral cells results in asynchronous recruitment of large populations of granule cells having reliable patterns of latencies, consistent with the idea that these patterns may play a role in shaping the slowly evolving temporal patterns of mitral cell activity.
One of the most remarkable aspects of our findings is that the latency of granule cell activity is reliable and specific to stimulation of a particular glomerulus. That is, glomerular identity is coded by the latency of granule cell firing. In an in vivo context, this observation would lead us to predict that granule cell latencies would be odor specific and thus that mitral cells might show reliable pauses in firing time locked to stimulus onset when stimulated with specific odorants. Such odor-specific patterns of mitral cell activity have in fact been observed and may be an important part of odor coding (Hamilton and Kauer, 1989; Wehr and Laurent, 1996; Luo and Katz, 2001; Margrie et al., 2001; Wilson et al., 2004). Although various circuit-level explanations have been proposed for such observations, our data suggest that the interaction of mitral and granule cells alone may be sufficient to explain these phenomena. Such slow changes in mitral cell activity also may result in time-dependent decorrelation of mitral cell activity (Friedrich and Laurent, 2001). This decorrelation of initially similar odor-evoked activity patterns into functionally distinct patterns develops over a timescale of hundreds of milliseconds (∼400 ms). Such time-dependent decorrelation requires consistent modulation of odor-evoked activity over prolonged periods after odor onset, such as could be achieved via the glomerulus-specific long-latency responses we report here.
Although such slow changes at the physiological level have not been directly tied to behavior, odor discrimination in rodents has been shown to occur during a period of between 200 and 550 ms after odor onset (Uchida and Mainen, 2003; Abraham et al., 2004), and some studies have found that the time depends on the difficulty of the task performed (Abraham et al., 2004; Rinberg et al., 2006). However, this result is somewhat controversial (Friedrich, 2006; Uchida et al., 2006). Our results show that brief mitral cell activity results in spiking in granule cells over this entire period. This delayed spiking suggests that, for several hundred milliseconds after mitral cell activity, the firing of granule cells will be sensitive to additional activity in mitral cells and also in their other inputs to granule cells (e.g., projections from cortical areas). That is, such long-latency activity gives the granule cell network a prolonged time window over which to integrate additional activity. The duration of this window may be sufficient to allow integration of information across successive sniff cycles and may be important for reliable relay of information to downstream neurons. Testing this network-level integration by patterned stimulation of mitral cells will be important to determine how this “smoldering” activity in granule cells influences the response to successive inputs.
Our results also raise the question of the mechanism by which these reliable long-latency responses are generated. In general, long-latency responses can be generated by slowly activating inward currents, such as persistent sodium currents or by slowly inactivating outward currents, such as A-type potassium currents. Inactivation of potassium channels generates long delays to spiking in many systems, and we have shown that blockade of A-current results in an ∼50% reduction in the latency of granule cell activity. Blockade of A-current also may affect other olfactory bulb neurons, but the concentration dependency of the effect that we observe suggests that it is mediated by Kv4.X potassium channels, which are expressed predominantly in granule cells. We do see that 4-AP makes mitral cells more likely to fire repeatedly after stimulation, but this would not explain the decreased latency of granule cell spiking. However, even after blockade of A-current, latencies are rather long (180 ms average) and rather widely distributed, suggesting that other mechanisms also contribute to long-latency spiking. Moreover, the inactivation time constant of A-current in granule cells has been measured to be in the tens of milliseconds (Schoppa and Westbrook, 1999), indicating that, although A-current is important for delaying spiking, the timing of the delay is not directly attributable to the inactivation but rather involves other mechanisms as well (Molineux et al., 2005). Similarly, the observation that a single granule cell may show very different latencies to stimulation of different glomeruli indicates that, if intrinsic properties determine the latency, they must interact differently with different inputs. An intriguing possibility is that input to different dendrites results in different latencies to spiking. If firing latencies are specific to the site at which synapses are made onto granule cell dendrites, then the role of A-current in prolonging spiking latencies could be attributable to differences in A-channel density on different dendritic branches.
Other candidate mechanisms include the combination of NMDA receptors (Schoppa et al., 1998; Chen et al., 2000; Halabisky et al., 2000) and voltage-gated calcium channels (Isaacson, 2001), both of which can generate relatively long-lasting responses under appropriate conditions. In our experiments, we use a low concentration of Mg2+ that will favor the activation of NMDA receptors. However, we have also seen long-latency granule cell activity in solutions containing 1.0 mm Mg2+ (our unpublished observations). Lowering Mg2+ increases substantially the number of active cells that we observe in response to single mitral cell or single glomerulus stimulation. Granule cells have been shown to fire low-threshold calcium spikes (Egger et al., 2003, 2005; Pinato and Midtgaard, 2003, 2005) that sometimes generate depolarizations in these cells lasting tens to hundreds of milliseconds. Even longer depolarizations have been observed in granule cells in amphibians, which are attributable in part to calcium-activated nonspecific cationic currents (Hall and Delaney, 2002). In most other systems, long latencies to spiking are associated with a high degree of temporal jitter, but this is not the case in our experiments on granule cell activity. Indeed, granule cells show remarkable reliability in their response latencies, even when the probability of firing is rather low. The fact that latencies are glomerulus specific indicates that the biophysical mechanisms that give rise to the long latencies must be in some respect input specific. This may be attributable to different inputs activating different dendritic branches of the granule cell (Zelles et al., 2006) or otherwise to different properties of synapses onto the granule cells. The biophysical mechanisms underlying this unique behavior are unclear, but understanding them will be important as we try to understand the functional role of granule cells in olfactory bulb circuitry.
A prediction of our data is that these long-latency granule cell spikes will alter the firing pattern of mitral cells, which will in turn alter granule cell latencies. That is, delayed inhibition by granule cells will eventually shape the activity of other granule cells. This dynamic feedback will be especially important in the case of prolonged mitral cell activity, including odor-evoked activity. Our observation that activity of different granule cells is only weakly correlated in single sweeps suggests that such dynamic feedback may be critical for generating coincident activity in populations of granule cells, as reported by Schoppa (2006) and, as has previously suggested, may be critical for synchronizing mitral cell firing (Lagier et al., 2004; Galan et al., 2006). Additional work on the interplay of ongoing granule and mitral cell activity will be needed to understand how these processes shape patterns of ongoing mitral cell activity.
Footnotes
This work was supported by National Institute on Deafness and Other Communication Disorders Grant RO1 DC005798. We thank Troy Margrie and Nicholas Fourcaud-Trocmé for helpful comments on this manuscript, Roberto Fernández Galán for help with statistical analysis, and Greg LaRocca for technical assistance.
References
- Abraham NM, Spors H, Carleton A, Margrie TW, Kuner T, Schaefer AT. Maintaining accuracy at the expense of speed: stimulus similarity defines odor discrimination time in mice. Neuron. 2004;44:865–876. doi: 10.1016/j.neuron.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Balu R, Larimer P, Strowbridge BW. Phasic stimuli evoke precisely timed spikes in intermittently discharging mitral cells. J Neurophysiol. 2004;92:743–753. doi: 10.1152/jn.00016.2004. [DOI] [PubMed] [Google Scholar]
- Barish ME. Differentiation of voltage-gated potassium current and modulation of excitability in cultured amphibian spinal neurones. J Physiol (Lond) 1986;375:229–250. doi: 10.1113/jphysiol.1986.sp016114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen WR, Xiong W, Shepherd GM. Analysis of relations between NMDA receptors and GABA release at olfactory bulb reciprocal synapses. Neuron. 2000;25:625–633. doi: 10.1016/s0896-6273(00)81065-x. [DOI] [PubMed] [Google Scholar]
- Egger V, Svoboda K, Mainen ZF. Mechanisms of lateral inhibition in the olfactory bulb: efficiency and modulation of spike-evoked calcium influx into granule cells. J Neurosci. 2003;23:7551–7558. doi: 10.1523/JNEUROSCI.23-20-07551.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egger V, Svoboda K, Mainen ZF. Dendrodendritic synaptic signals in olfactory bulb granule cells: local spine boost and global low-threshold spike. J Neurosci. 2005;25:3521–3530. doi: 10.1523/JNEUROSCI.4746-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrich RW. Mechanisms of odor discrimination: neurophysiological and behavioral approaches. Trends Neurosci. 2006;29:40–47. doi: 10.1016/j.tins.2005.10.004. [DOI] [PubMed] [Google Scholar]
- Friedrich RW, Laurent G. Dynamic optimization of odor representations by slow temporal patterning of mitral cell activity. Science. 2001;291:889–894. doi: 10.1126/science.291.5505.889. [DOI] [PubMed] [Google Scholar]
- Friedrich RW, Habermann CJ, Laurent G. Multiplexing using synchrony in the zebrafish olfactory bulb. Nat Neurosci. 2004;7:862–871. doi: 10.1038/nn1292. [DOI] [PubMed] [Google Scholar]
- Galan RF, Fourcaud-Trocme N, Ermentrout GB, Urban NN. Correlation-induced synchronization of oscillations in olfactory bulb neurons. J Neurosci. 2006;26:3646–3655. doi: 10.1523/JNEUROSCI.4605-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halabisky B, Friedman D, Radojicic M, Strowbridge BW. Calcium influx through NMDA receptors directly evokes GABA release in olfactory bulb granule cells. J Neurosci. 2000;20:5124–5134. doi: 10.1523/JNEUROSCI.20-13-05124.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall BJ, Delaney KR. Contribution of a calcium-activated non-specific conductance to NMDA receptor-mediated synaptic potentials in granule cells of the frog olfactory bulb. J Physiol (Lond) 2002;543:819–834. doi: 10.1113/jphysiol.2002.024638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton KA, Kauer JS. Patterns of intracellular potentials in salamander mitral/tufted cells in response to odor stimulation. J Neurophysiol. 1989;62:609–625. doi: 10.1152/jn.1989.62.3.609. [DOI] [PubMed] [Google Scholar]
- Ikegaya Y, Aaron G, Cossart R, Aronov D, Lampl I, Ferster D, Yuste R. Synfire chains and cortical songs: temporal modules of cortical activity. Science. 2004;304:559–564. doi: 10.1126/science.1093173. [DOI] [PubMed] [Google Scholar]
- Isaacson JS. Mechanisms governing dendritic gamma-aminobutyric acid (GABA) release in the rat olfactory bulb. Proc Natl Acad Sci USA. 2001;98:337–342. doi: 10.1073/pnas.021445798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacson JS, Strowbridge BW. Olfactory reciprocal synapses: dendritic signaling in the CNS. Neuron. 1998;20:749–761. doi: 10.1016/s0896-6273(00)81013-2. [DOI] [PubMed] [Google Scholar]
- Jahr CE, Nicoll RA. Dendrodendritic inhibition: demonstration with intracellular recording. Science. 1980;207:1473–1475. doi: 10.1126/science.7361098. [DOI] [PubMed] [Google Scholar]
- Lagier S, Carleton A, Lledo PM. Interplay between local GABAergic interneurons and relay neurons generates gamma oscillations in the rat olfactory bulb. J Neurosci. 2004;24:4382–4392. doi: 10.1523/JNEUROSCI.5570-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurent G. A systems perspective on early olfactory coding. Science. 1999;286:723–728. doi: 10.1126/science.286.5440.723. [DOI] [PubMed] [Google Scholar]
- Laurent G, Wehr M, Davidowitz H. Temporal representations of odors in an olfactory network. J Neurosci. 1996;16:3837–3847. doi: 10.1523/JNEUROSCI.16-12-03837.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurent G, Stopfer M, Friedrich RW, Rabinovich MI, Volkovskii A, Abarbanel HD. Odor encoding as an active, dynamical process: experiments, computation, and theory. Annu Rev Neurosci. 2001;24:263–297. doi: 10.1146/annurev.neuro.24.1.263. [DOI] [PubMed] [Google Scholar]
- Luo M, Katz LC. Response correlation maps of neurons in the Mammalian olfactory bulb. Neuron. 2001;32:1165–1179. doi: 10.1016/s0896-6273(01)00537-2. [DOI] [PubMed] [Google Scholar]
- MacLeod K, Laurent G. Distinct mechanisms for synchronization and temporal patterning of odor-encoding neural assemblies. Science. 1996;274:976–979. doi: 10.1126/science.274.5289.976. [DOI] [PubMed] [Google Scholar]
- Margrie TW, Sakmann B, Urban NN. Action potential propagation in mitral cell lateral dendrites is decremental and controls recurrent and lateral inhibition in the mammalian olfactory bulb. Proc Natl Acad Sci USA. 2001;98:319–324. doi: 10.1073/pnas.011523098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molineux ML, Fernandez FR, Mehaffey WH, Turner RW. A-type and T-type currents interact to produce a novel spike latency-voltage relationship in cerebellar stellate cells. J Neurosci. 2005;25:10863–10873. doi: 10.1523/JNEUROSCI.3436-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterlin ZA, Kozloski J, Mao BQ, Tsiola A, Yuste R. Optical probing of neuronal circuits with calcium indicators. Proc Natl Acad Sci USA. 2000;97:3619–3624. doi: 10.1073/pnas.97.7.3619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinato G, Midtgaard J. Regulation of granule cell excitability by a low-threshold calcium spike in turtle olfactory bulb. J Neurophysiol. 2003;90:3341–3351. doi: 10.1152/jn.00560.2003. [DOI] [PubMed] [Google Scholar]
- Pinato G, Midtgaard J. Dendritic sodium spikelets and low-threshold calcium spikes in turtle olfactory bulb granule cells. J Neurophysiol. 2005;93:1285–1294. doi: 10.1152/jn.00807.2004. [DOI] [PubMed] [Google Scholar]
- Price JL, Powell TP. The synaptology of the granule cells of the olfactory bulb. J Cell Sci. 1970;7:125–155. doi: 10.1242/jcs.7.1.125. [DOI] [PubMed] [Google Scholar]
- Rall W, Shepherd GM, Reese TS, Brightman MW. Dendrodendritic synaptic pathway for inhibition in the olfactory bulb. Exp Neurol. 1966;14:44–56. doi: 10.1016/0014-4886(66)90023-9. [DOI] [PubMed] [Google Scholar]
- Rinberg D, Koulakov A, Gelperin A. Speed-accuracy tradeoff in olfaction. Neuron. 2006;51:351–358. doi: 10.1016/j.neuron.2006.07.013. [DOI] [PubMed] [Google Scholar]
- Schoppa NE. Synchronization of olfactory bulb mitral cells by precisely timed inhibitory inputs. Neuron. 2006;49:271–283. doi: 10.1016/j.neuron.2005.11.038. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, Urban NN. Dendritic processing within olfactory bulb circuits. Trends Neurosci. 2003;26:501–506. doi: 10.1016/S0166-2236(03)00228-5. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, Westbrook GL. Regulation of synaptic timing in the olfactory bulb by an A-type potassium current. Nat Neurosci. 1999;2:1106–1113. doi: 10.1038/16033. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, Kinzie JM, Sahara Y, Segerson TP, Westbrook GL. Dendrodendritic inhibition in the olfactory bulb is driven by NMDA receptors. J Neurosci. 1998;18:6790–6802. doi: 10.1523/JNEUROSCI.18-17-06790.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serodio P, Rudy B. Differential expression of Kv4 K+ channel subunits mediating subthreshold transient K+ (A-type) currents in rat brain. J Neurophysiol. 1998;79:1081–1091. doi: 10.1152/jn.1998.79.2.1081. [DOI] [PubMed] [Google Scholar]
- Shepherd GM, Greer CA. Olfactory bulb. In: Shepherd , editor. The synaptic organization of the brain. New York: Oxford UP; 1998. [Google Scholar]
- Shimshek DR, Bus T, Kim J, Mihaljevic A, Mack V, Seeburg PH, Sprengel R, Schaefer AT. Enhanced odor discrimination and impaired olfactory memory by spatially controlled switch of AMPA receptors. PLoS Biol. 2005;3:e354. doi: 10.1371/journal.pbio.0030354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stopfer M, Laurent G. Short-term memory in olfactory network dynamics. Nature. 1999;402:664–668. doi: 10.1038/45244. [DOI] [PubMed] [Google Scholar]
- Stopfer M, Bhagavan S, Smith BH, Laurent G. Impaired odour discrimination on desynchronization of odour-encoding neural assemblies. Nature. 1997;390:70–74. doi: 10.1038/36335. [DOI] [PubMed] [Google Scholar]
- Stopfer M, Jayaraman V, Laurent G. Intensity versus identity coding in an olfactory system. Neuron. 2003;39:991–1004. doi: 10.1016/j.neuron.2003.08.011. [DOI] [PubMed] [Google Scholar]
- Uchida N, Mainen ZF. Speed and accuracy of olfactory discrimination in the rat. Nat Neurosci. 2003;6:1224–1229. doi: 10.1038/nn1142. [DOI] [PubMed] [Google Scholar]
- Uchida N, Kepecs A, Mainen ZF. Seeing at a glance, smelling in a whiff: rapid forms of perceptual decision making. Nat Rev Neurosci. 2006;7:485–491. doi: 10.1038/nrn1933. [DOI] [PubMed] [Google Scholar]
- Urban NN. Lateral inhibition in the olfactory bulb and in olfaction. Physiol Behav. 2002;77:607–612. doi: 10.1016/s0031-9384(02)00895-8. [DOI] [PubMed] [Google Scholar]
- Urban NN, Sakmann B. Reciprocal intraglomerular excitation and intra- and interglomerular lateral inhibition between mouse olfactory bulb mitral cells. J Physiol (Lond) 2002;542:355–367. doi: 10.1113/jphysiol.2001.013491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wehr M, Laurent G. Odour encoding by temporal sequences of firing in oscillating neural assemblies. Nature. 1996;384:162–166. doi: 10.1038/384162a0. [DOI] [PubMed] [Google Scholar]
- Wehr M, Laurent G. Relationship between afferent and central temporal patterns in the locust olfactory system. J Neurosci. 1999;19:381–390. doi: 10.1523/JNEUROSCI.19-01-00381.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson RI, Turner GC, Laurent G. Transformation of olfactory representations in the Drosophila antennal lobe. Science. 2004;303:366–370. doi: 10.1126/science.1090782. [DOI] [PubMed] [Google Scholar]
- Yokoi M, Mori K, Nakanishi S. Refinement of odor molecule tuning by dendrodendritic synaptic inhibition in the olfactory bulb. Proc Natl Acad Sci USA. 1995;92:3371–3375. doi: 10.1073/pnas.92.8.3371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zelles T, Boyd JD, Hardy AB, Delaney KR. Branch-specific Ca2+ influx from Na+-dependent dendritic spikes in olfactory granule cells. J Neurosci. 2006;26:30–40. doi: 10.1523/JNEUROSCI.1419-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]