Surface tension determines tissue shape and growth kinetics (original) (raw)
Growing tissues exhibit liquid-like behavior, which allows them to respond to macroscopic surface curvatures.
Abstract
The collective self-organization of cells into three-dimensional structures can give rise to emergent physical properties such as fluid behavior. Here, we demonstrate that tissues growing on curved surfaces develop shapes with outer boundaries of constant mean curvature, similar to the energy minimizing forms of liquids wetting a surface. The amount of tissue formed depends on the shape of the substrate, with more tissue being deposited on highly concave surfaces, indicating a mechano-biological feedback mechanism. Inhibiting cell-contractility further revealed that active cellular forces are essential for generating sufficient surface stresses for the liquid-like behavior and growth of the tissue. This suggests that the mechanical signaling between cells and their physical environment, along with the continuous reorganization of cells and matrix is a key principle for the emergence of tissue shape.
INTRODUCTION
The growth of tissue is an essential process controlling morphogenesis and regeneration of organs (1). In general, tissue-forming cells are interactive and motile (2), which can give rise to emergent physical properties, such as viscous fluid behavior, as has been shown for epithelial monolayers during embryogenesis (3, 4) and for cell agglomerates (5) with a measurable surface tension (6). However, the mechanical integrity of tissues is provided by extracellular matrices (ECMs) that turn tissues into solids with well-defined elastic properties (7). Paradoxically, it has been shown by in vitro experiments that even osteoid-like tissue with large amounts of ECM grows according to rules reminiscent of fluid behavior (8, 9).
Motivated by this conundrum, we show here quantitatively, by constraining growing tissues to surfaces of controlled mean curvature, that osteoid-like tissues develop shapes similar to the equilibrium shapes of fluids (10). In particular, for geometries with rotational symmetry, the tissue stays bounded by surfaces of constant mean curvature and grows with rates depending on surface curvature. Perturbating cytoskeletal tension revealed that cell contractility is responsible for generating the necessary surface stresses. This indicates that continuous remodeling of the solid matrix combined with the contractility of bone-forming cells provides sufficient effective fluidity and surface stress required for a fluid-like behavior of the growing tissue at the time scale of days to weeks. Our work demonstrates that morphogenesis shares fundamental physical principles with fluid droplets, as first suggested in Thompson’s seminal work On Growth and Form (11).
Single cells respond to the dimensionality of their environment (12, 13), with notable differences between cells on flat surfaces and those surrounded by a three-dimensional (3D) environment (14). In vivo, cells are unlikely being constrained to flat surfaces (15), but as long as the curvature is small, cells may behave as if the surface is flat (16). For cell agglomerates and tissues, the situation is different, as cells can then mechanically interact with each other as well as with their physical environment (17–19). They may even collectively sense and respond to macroscopic surface curvature (8, 9). The geometry of the environment strongly influences cell behavior, because it determines the spatial distribution of force patterns that cells sense and transmit. Previous studies on the role of surface curvature on cell and tissue behavior focused on surfaces where one of the principal curvatures is zero (8, 20, 21) or was not quantitative due to the complexity of the scaffolds (22). Here, we address this problem by growing tissue on scaffolds with rotational symmetry and constant mean curvature. These scaffolds were obtained by shaping liquid polydimethylsiloxane (PDMS) through surface tension using a method adapted from Wang and McCarthy (23). Briefly, a liquid polymer drop is placed between two solid discs and forms a capillary bridge (CB), with a shape that minimizes its total surface area according to the Laplace-Young law (figs. S1 and S2) before it solidifies. The mean curvature of the CB can be precisely tuned by varying bridge height, liquid volume, and disc diameters (figs. S1 and S2). Under these conditions, the CB obtains a rotational symmetric surface that belongs to a special class of constant mean curvature surfaces called “Delaunay surfaces” (fig. S2A) (10). Consequently, if tissue grows on a rotationally symmetric 3D support (such as the PDMS CBs), one must expect it to morph into shapes that resemble Delaunay surfaces at any time during the growth process.
Tissues growing on the curved surfaces obtain shapes similar to liquids
To investigate the shape developed by a growing tissue, osteoid-like tissue was grown on these PDMS scaffolds using a preosteoblastic cell line (MC3T3-E1), which has been demonstrated to synthesize a collagen-rich extracellular matrix (ECM) (8, 9). In particular, these preosteoblasts have been shown to respond to the local curvature of the substrate by depositing significantly more ECM on concave surfaces compared to flat or convex surfaces. Although similar behavior has been observed for fibroblasts and mesenchymal stem cells (22, 24), we chose to focus this work on the well-studied MC3T3-E1 preosteoblast cells to explore growth on our novel constant mean curvature substrates. Tissue growing on the curved surface was pinned to the flat edges of the bridge (Fig. 1A, red circle). In addition, the tissue growing in between the CB and the sample holder formed an almost constant angle with the flat surfaces. Both observations are reminiscent of liquid wetting. For a constant height of the CBs, the average thickness of tissue formed after about 1 month of culture was observed to decrease with increasing neck radius of the CB (Fig. 1, B, C, F to I, and J to L). In addition, the tissue surfaces were shown to be rotational symmetric using 3D light-sheet fluorescence microscopy (LSFM) imaging of fixed tissues (Fig. 1, B to E, and movie S1). This rotational symmetry allowed us to estimate tissue volume and mean curvature from 2D images. To explore the behavior of the growing tissue, we plotted mean curvatures and surface areas of the tissue as a function of total volume (CB volume plus tissue) and compared this to theoretical predictions of the Laplace-Young law for a liquid drop adhering to the scaffold using the software package Surface Evolver (Fig. 2, A and B) (25). Briefly, Surface Evolver uses a surface energy minimization scheme to predict the shape of liquid interfaces that are subject to surface tension (see the “Estimating surface profiles of liquid interfaces using Surface Evolver” section in Materials and Methods). Liquid-like behavior was then also demonstrated for CBs with smaller end spacings (Fig. 2, C and D) that cover a larger range of mean curvature. Our experimental results perfectly match the theoretical predictions obtained from Surface Evolver (shaded area in Fig. 2, A to D), providing strong experimental evidence that growing osteoid-like tissues behave like fluids at time scales relevant for growth.
Fig. 1. CB geometry as a means to control 3D tissue growth.
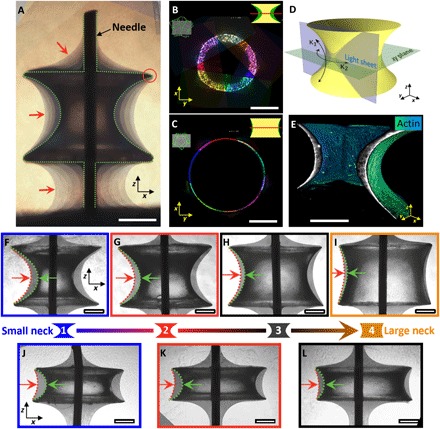
(A) Composition of phase-contrast images of tissues grown on a CB taken after 4, 7, 21, 32, 39, and 47 days. The tissue is pinned at the edges of the CB (red circle) and shows a moving contact line in between the scaffold and the Teflon holder, reminiscent of a liquid. Dashed line indicates the CB surface, and red arrows point toward the tissue-medium interface. Scale bar, 500 μm. (B and C) Radial slices at the neck for two different CB sizes with initial volumes of 1.1 μl (B) and 2.8 μl (C) obtained with LSFM from five different views. (D) Sample geometry and orientation of the light sheet. κ1and κ2 are minimum and maximum principal curvatures. (E) 3D rendering of actin fibers on the sample shown in (F) color-coded according to fluorescence intensity. (F to I) Phase-contrast images of tissues grown on four different CB surfaces with initial volumes of 1.1 μl (F), 1.6 μl (G), 2.2 μl (H), and 2.8 μl (I). (J to L) CB surfaces with initial volumes of 1.1 μl (J), 1.3 μl (K), and 1.5 μl (L). Sample neck size increases from left to right. Green arrow indicates the interface of the initial shape, and red arrow indicates the position of the tissue-medium interface after 32 days. Scale bars, 400 μm.
Fig. 2. Tissues behave like liquids when constrained by curved surfaces.
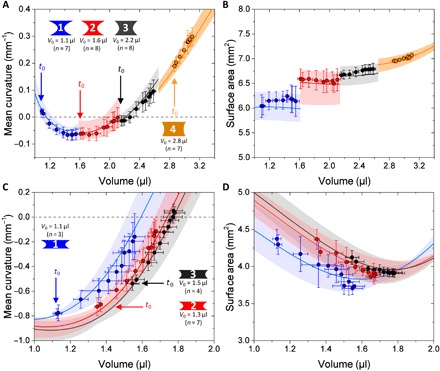
(A to D) Evolution of the surface mean curvature (A and C) and surface area (B and D) of the tissue interfaces as a function of total volume (CB volume _V_0 plus tissue volume) for the two different CB shapes shown in Fig. 1. (A and B) Tissues grown on CB surfaces with a height of ~1.2 mm and top/bottom radius of ~1 mm with initial volumes of 1.1 μl (size 1; blue), 1.6 μl (size 2; red), 2.2 μl (size 3; black), and 2.8 μl (size 4; orange). Colored areas delineate the theoretical predictions of liquid interfaces of the same dimension based on the scaffold geometries obtained from the experiment. Colored curves are the corresponding mean values. (C and D) Tissues grown on CB surfaces with a height of ~0.7 mm and top/bottom radius of ~1 mm with initial volumes of 1.1 μl (size 1; blue), 1.3 μl (size 2; red), and 1.5 μl (size 3; black). Curves are color-coded according to the corresponding theoretical predictions of the liquid interface (see the Supplementary Materials for the full data).
Cell contractility is required for developing surface tension
To investigate the influence of cell contractility on the liquid-like behavior of the tissue and the kinetics of growth, we performed various chemical treatments to either down- or up-regulate cytoskeletal contractility through supplementation of the myosin II inhibitor blebbistatin or transforming growth factor–β1 (TGF-β1). Enhancing cell contractility via TGF-β1 resulted in an increased tissue volume, whereas cells treated with blebbistatin deposited a decreasing amount of tissue in the order of increasing blebbistatin concentration (fig. S4). This demonstrates that the tissue volume formed by MC3T3-E1 cells on constant mean curvature surfaces depends on cytoskeletal tension. Moreover, the shape of the tissues that were treated with blebbistatin significantly deviate from the predictions of the Laplace-Young law, whereas samples treated with TGF-β1 resemble theoretical predictions. This suggests that cell contractility is essential for generating the necessary surface stresses of the growing tissue (fig. S4).
This is in line with recent observations in tissue monolayers, where an enhanced expression of cadherins (adhesion molecules) leads to an increase in surface tension not only through an increase of cell-cell contacts but also through an up-regulation of actomyosin contractility (26). The progressive increase in tissue tension resulted in a wetting transition similar to a liquid drop wetting a surface, which could be reversed by inhibiting myosin contractility, suggesting that the increase in tissue surface tension arises from active contractile forces and not from adhesion energies.
The kinetics of tissue growth depend on the surface curvature
We next investigated whether the kinetics of tissue growth is controlled by surface curvature. By studying various CB shapes, we found that the tissue volume formed after 32 days depends on the CB neck radius, with higher growth rates observed for thin-necked CBs (Fig. 3A). In all cases, the tissue growth rate showed a similar behavior as a function of time: It gradually increased until reaching a maximum after about 2 weeks of tissue culture and then slowed down at later time points. As a consequence, data obtained from different experiments with various CB geometries can be collapsed to one master curve by rescaling the tissue volume _V_T with the volume at the end of the experiment (_V_T*) (Fig. 3B). To account for differences in initial cell number after seeding onto the scaffold, we further normalized the final tissue volume (_V_T*) by the initial surface area (_A_0), which yields the average final tissue thickness (_V_T*/A_0). The plot in Fig. 3C reveals that the final tissue thickness correlates with the minimum principal curvature (κmin, concave curvature) of the scaffold, in agreement with previous observations on cylindrical pores (8). To assess the time-dependent slowdown of tissue growth, we normalized the growth rates by the current tissue volume to obtain the exponential growth rate (d_V_T/d_t)/_V_T = d(ln(_V_T/V_T,0)/d_t, plotted in Fig. 3D. Exponential growth would correspond to constant d(ln(_V_T/V_T,0)/d_t, as expected, if the rate of cell division was constant over time. This exponential growth rate (or volume strain rate, in mechanical terminology) decreases according to a master curve independent of geometry (Fig. 3D). This suggests that it is related to biochemical signaling or tissue maturation intrinsic to osteoblasts (27) but independent of tissue shape.
Fig. 3. The kinetics of tissue growth depend on the initial curvature.
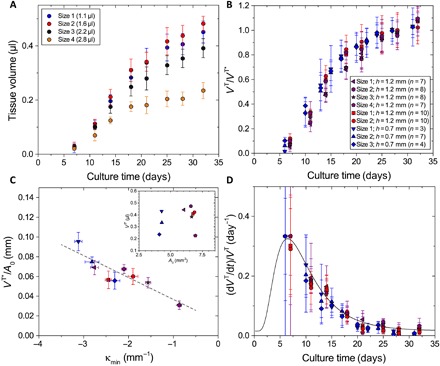
(A) Measured tissue volumes for the four different CBs presented in Fig. 1 (F to I) with initial volumes of 1.1 μl (size 1; blue), 1.6 μl (size 2; red), 2.2 μl (size 3; black), and 2.8 μl (size 4; yellow). (B) Rescaling of the current tissue volume _V_T with the maximum tissue volume _V_T* (average of days 24 to 32) for three independent experiments and different CB shapes. Data points are color-coded according to the experiment, where each symbol represents a different CB shape. (C) Average tissue thickness _V_T*/_A_0 as a function of initial minimum principal curvature κmin and a linear regression (gray line; R = –0.936). Inset shows the initial surface area _A_0. (D) Rate of growth per tissue volume as a function of culture time, which can be fitted with a decay function following a standard log-normal distribution (black curve).
Cells self-organize into left-handed chiral patterns
Finally, we investigated the influence of surface curvature on the tissue microstructure using 3D LSFM and actin staining of the tissue. This revealed the formation of chiral actin fiber patterns that exhibit a clear left-handedness (Fig. 4A) in all examined samples (n = 12; see also fig. S9). The actin fibers follow locally straight-line paths over the curved surface and consistently spiral around the sample at ~60° with respect to the circumferential direction at the neck (Fig. 4B), nearly independently of the CB shape (Fig. 4C). We have conducted two independent additional experiments (data available upon request) in which we also recovered the same close to 60° orientation angle in most of the samples, suggesting that the chirality is robust.
Fig. 4. Spontaneous emergence of chiral structures.
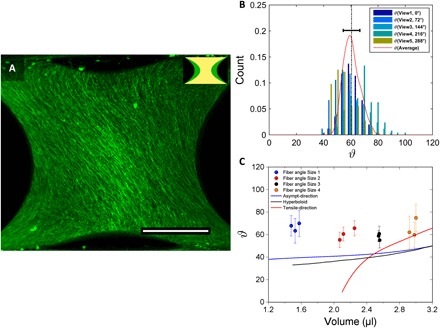
(A) Maximum projection of tissue grown on a CB with an initial volume of 1.1 μl imaged after 32 days of tissue culture. Tissues were stained for actin and visualized using LSFM. Actin fibers are oriented in a particular direction. Scale bar, 500 μm. (B) Example of the fiber angle distributions for five different views (72° increments) around the sample obtained using fast Fourier transform analysis. Red curve delineates the average fiber angle distribution over all views, and dashed line indicates the mean value. (C) Mean fiber angle distributions as a function of total volume for four different sample sizes (color-coded; n = 3) compared to asymptotic directions of corresponding CB surfaces (blue curve) and to hyperboloid surfaces (black curve). Red curve shows theoretical predictions of maximum tensile directions obtained using membrane theory.
We next quantified the time progression of the fiber angle distribution using a live actin stain to pinpoint when symmetry breaks. Cells start aligning along the CB axis within the first 5 days. After a transition phase at day 10, where cells are mostly randomly organized, cells start to form left-handed chiral structures at around day 15 (see fig. S10).
To interpret this, we investigated three possible hypotheses: First, surface stress in doubly curved surfaces is not homogeneous with respect to the in-plane stress direction. For surfaces with negative Gaussian curvature, the local stress tensor can be decomposed into two normal components, where one component has zero stress and the other (perpendicular to it) carries a tangential load. This would mean that the complete surface stress could be transferred just by pulling along this tangential direction with no load perpendicular to it (see the “Theory of membrane forces in thin shells applied to capillary bridge surfaces” section in the Supplementary Materials). The red line in Fig. 4C corresponds to this favored loading direction. The curve is not defined at small volumes where the mean curvature is such that no zero stress direction exists. Second, we hypothesize that spindle-shaped cells align with the direction of zero curvature (see the “Asymptotic directions on hyperboloids and capillary bridge surfaces” section in the Supplementary Materials). This is inspired from recent observations where fibroblast cells have been shown to behave like active nematic liquid crystals on flat surfaces (28). This would suggest that cells minimize their free energy by aligning with locally straight directions (Fig. 4C, blue curve) to obtain an optimal packing on the surface. Third, we approximated the doubly curved surface near the neck by a hyperboloid that is actually a ruled surface generated by a straight line moving through space (see the “Asymptotic directions on hyperboloids and capillary bridge surfaces” section in the Supplementary Materials). The black line in Fig. 4C corresponds to the direction of the generating straight line. However, none of these three hypotheses gives a perfect fit to the data (Fig. 4C). The red line (hypothesis 1) is not even defined over the whole range where the chiral patterns were observed. This seems to rule out a purely mechanical origin of the phenomenon and rather suggests liquid crystal–like behavior. Fibroblasts seeded on concave surfaces have been observed to align preferentially at a certain angle and thus at a certain curvature, which minimizes compression forces on the nucleus (29). This could explain why cells do not follow the zero curvature (asymptotic) directions but prefer a slightly concave direction. Nevertheless, this long-range collective cell alignment also determines the orientation of the collagen fibers that are secreted by the cells, which has a direct impact on the mechanical properties and load distribution of the developed/mature tissue (30). The preference for only one of the asymptotic directions is unresolved but might be related to the intrinsic cell chirality reported for preosteoblasts, which exhibit a counterclockwise orientation when seeded on ring-shaped patterns (31).
CONCLUSIONS
Our model system gives quantitative evidence that osteoid-like tissues can make use of the physics of fluids to generate complex 3D patterns, corresponding to equilibrium shapes with constant mean curvature. However, we also observed a long-range cell alignment with a chirality of aligned actin filaments that could preconfigure the orientation of collagen fibrils that form similar patterns in osteons (32, 33). These large-scale fiber arrangements also occur in heart tissue where myocardial fibers are organized into a helical muscle band structure (34). The ability to make scaffolds of defined 3D curvature is highly relevant, because many biological surfaces are doubly curved (35), with examples including trabecular bone (36) and gyroid structures in butterflies (37). Our findings about the role of fluidity and surface stresses could potentially also contribute to the understanding of more complex tissue structures, such as organoids, and may motivate innovative scaffold designs for tissue engineering applications.
MATERIALS AND METHODS
Fabrication of PDMS scaffolds of constant mean curvature
PDMS scaffolds were prepared using a method adapted from Wang and McCarthy (23), who fabricated solid CBs using epoxy resin. In our study, CBs were made using the Dow Corning Sylgard 184 Silicone Elastomer Kit. Base and curing agent were mixed in a ratio of 9:1, by weight. After thorough stirring for at least 3 min, the solution was degassed under vacuum to remove entrapped gas bubbles and then poured onto a glass coverslip and allowed to spread until the solution has formed a homogenous layer. CBs were then generated between CNC machined cylindrical aluminum posts of equal radius (1 mm) as follows (fig. S1): The PDMS mixture is briefly brought in contact with the posts and then withdrawn, resulting in spherical shaped droplets. The PDMS covered posts were then brought into contact with opposing posts to form CBs. The finite height of the CBs was thereby fine-tuned by adjusting the plate separation distance by means of a screw (fig. S1A) and then maintained at a constant value throughout the experiment using aluminum spacers.
The liquid bridges were subsequently cured at 120°C for 20 min in an oven. Scaffolds of identical height but different volumes of PDMS can thus be generated by keeping a constant displacement of the posts and controlling the initial droplet size. Each scaffold has a surface of constant mean curvature. Owing to the simple procedure, however, precise control over the droplet volume was not possible. Instead, large numbers of CBs of different volumes were produced, and their volume was determined using a method described below (see the “Estimating the tissue volume and surface mean curvature” section below).
The dimensions of the CBs were chosen such that the shape is largely determined by effects from surface stress, meaning that gravitational forces can be neglected. This is the case for Bond numbers, B ≡ ∆ρ_gl_2/γ ≪ 1, where ∆ρ is the density difference, g is the gravitational constant, l is the plate separation, and γ is the surface stress (10). The Bond number of the PDMS CBs was calculated to be in the range of B = (8.4 ± 1.4)10−4, for bridges formed between circular discs of 2 mm diameter with a plate separation distance of 1.25 mm, using surface tension values of (18 ± 3) mN/m determined by Dee and Sauer (38) for temperature ranges between 25° and 125°C, and assuming a constant polymer density of 0.982 kg m−3 (39).
Preparing PDMS CBs for tissue culture
Scaffolds were attached to a custom-built Teflon holder using ultrathin acupuncture needles (Wandrey Premium acupuncture needles, NPPR1630) with a diameter of d = 160 μm so that the CBs have their symmetry axis perpendicular to the viewing direction.
Functionalization of PDMS scaffolds with fibronectin
To support cell attachment, surfaces were modified by covalently binding fibronectin to the PDMS scaffolds following a method described by Tan and Desai (40). This method uses (3-aminopropyl)triethoxysilane (APTES) and cross-linker glutaraldehyde (GA) chemistry to immobilize fibronectin on PDMS. Before the surface treatment, PDMS scaffolds were thoroughly washed in distilled water, rinsed with ethanol, and then dried at room temperature. Scaffold treatment was initiated via oxygen air plasma activation using a plasma cleaner (Harrick Plasma PDC-002) for a period of 60 s at a pressure of 0.36 mbar and a coil power of 30 W. Immediately following air plasma treatment, scaffolds were covered with 3% APTES in double-distilled water (ddH2O) for 15 min and then thoroughly washed with ddH2O. Subsequently, scaffolds were incubated with 1% GA in ddH2O for 30 min and again thoroughly washed with ddH2O. Last, scaffolds were incubated with fibronectin in phosphate-buffered saline (PBS) at a concentration of 50 μg/ml for 1 hour at room temperature and then extensively washed with PBS to remove nonattached fibronectin residues.
Procedure of culturing cells on PDMS scaffolds
Murine preosteoblastic cells MC3T3-E1 (provided by the Ludwig Boltzmann Institute of Osteology, Vienna, Austria) were seeded on top of the PDMS surfaces with a density of 1 × 105 cells/cm2 and then cultured in α-minimum essential medium (MEM) (Sigma-Aldrich, St. Louis, MO) with d-glucose (4500 mg/liter; Sigma-Aldrich, Germany) supplemented with fetal calf serum (10%; PAA Laboratories, Linz, Austria), ascorbic acid (50 μg/ml; Sigma-Aldrich, St. Louis, MO), and gentamicin (0.1%; Sigma-Aldrich, Steinheim, Germany). Scaffolds containing cells were then incubated at 37°C in a humidified atmosphere with 5% CO2. After the first 3 days of tissue culture, scaffolds were transferred into a new culture plate and the culture medium was then changed every 3 to 4 days throughout the experiment.
Perturbation of cell contractility
To investigate the effect of cell contractility on the shape of the tissues, we performed the following treatments to either down- or up-regulate cytoskeletal contractility. To reduce cell contractility, tissues were incubated in α-MEM supplemented with the myosin II inhibitor blebbistatin (Sigma-Aldrich, Steinheim, Germany) at final concentrations of 2, 5, and 10 μM, including 0.2% dimethyl sulfoxide (Sigma-Aldrich, St. Louis, MO). To enhance cell contractility, tissues were incubated with TGF-β1 (Invitrogen, MD) at a final concentration of 1 ng/ml. All treatments were performed throughout the culture starting at day 4 of tissue culture up until the end of the experiment.
Fluorescence staining
At the end of each tissue culture experiment, the scaffolds were washed in PBS and subsequently fixed in 4% paraformaldehyde for 10 min at room temperature. Following fixation, tissues were then permeabilized overnight in 1% Triton X-100 (Sigma-Aldrich) at 4°C. After washing again in PBS, the cell cytoskeleton was stained for actin stress fibers by incubating them in a solution of Alexa Fluor 488 phalloidin (excitation wavelength, 488 nm) (Invitrogen, Molecular Probes) at a concentration of 3 × 10−7 M for 90 min in the dark. To stain the cell nuclei, the samples were incubated for 5 min in TO-PRO 3 iodide (excitation wavelength, 633 nm) (Invitrogen, Molecular Probes) at a concentration of 3 × 10−6 M. Before imaging, the samples were intensively washed in PBS and subsequently imaged with a light-sheet fluorescence microscope (Lightsheet Z.1, Zeiss) equipped with a 10× 0.5-NA water immersion objective lens, using an argon-ion laser at 488 nm and a helium-neon laser at 633 nm to visualize actin and cell nuclei, respectively.
Live cell imaging
Standard α-MEM was exchanged with α-MEM supplemented with 100 nM SiR-actin (633 nm, Spirochrome, Switzerland) and 10 μM verapamil (Spirochrome, Switzerland) 24 hours before imaging and then incubated at 37°C in a humidified atmosphere with 5% CO2. Samples were imaged after 5, 10, 15, and 32 days of tissue culture with a Leica SP8 confocal microscope using a 25× 0.95-NA water immersion objective lens (Leica Fluotar VISIR) and a helium-neon laser at 633 nm. After each imaging cycle, medium containing SiR-actin was exchanged with standard α-MEM to reduce prolonged SiR-actin exposure.
Estimating the tissue volume and surface mean curvature
The CB scaffolds containing cells and tissues were imaged perpendicular to the symmetry axis using a phase-contrast microscope. The images were then analyzed using a custom code written in MATLAB R2015b (MathWorks, Natick, MA) to estimate the volume and surface mean curvature from the profile curves of the 2D shape. The script works as follows: A black and white image was generated from the phase-contrast image of the CB by thresholding. The region of interest containing only the CB (and tissue) was then manually selected. A fourth-degree polynomial was used for fitting the surface points on both sides of the CB and generating a surface of revolution. The volume of the CB (plus tissue) was taken to be the total volume inside the surface of revolution. The volume was calculated directly from the 2D image using pixel distance to centerline. The volume of the CB was then given by V = _p_S ⋅ π∑_iri_2, where _p_S is the pixel size (2.415 μm) and ri is the distance of pixel i to the centerline.
To calculate the mean curvature, the surface of revolution was discretized in a quadrangular surface mesh. The local mean curvature was obtained from coefficients of the fundamental forms by calculating the local gradients at each vertex point of the mesh. The mean curvature of the surface was then obtained by averaging the estimated local mean curvature at each vertex point of the quadrangular (rectangular) surface mesh. The surface area of each CB was obtained from the mesh area. Estimated values of the volume, surface area, and surface mean curvature of the profile curves on both sides of the shape were averaged to yield values for the surface mean curvature, volume, and area of the CB (fig. S3).
Estimating surface profiles of liquid interfaces using Surface Evolver
The software package Surface Evolver (41) was used to estimate the volume, surface area, and pressure actin on the surface area of CBs (fig. S3). The bridge shapes were calculated numerically by minimizing the surface energy for a fixed volume constrained to the outer edges of two fixed circular plates centered along one axis of revolution. The simulation was considered as having reached convergence when the rate of energy change was consistently less than one part per million. Exemplary equilibrium shapes of liquid bridges are shown in fig. S2A. The mean curvature of each CB volume was calculated from the resultant pressure acting on the bridge surfaces using the Laplace-Young equation. Figure S2B reports their corresponding surface mean curvature and surface area.
Supplementary Material
http://advances.sciencemag.org/cgi/content/full/5/9/eaav9394/DC1
Download PDF
Movie S1
Surface tension determines tisue shape and growth kinetics
Acknowledgments
We thank C. Pilz for help in the tissue culture experiments and D. Accardi and T. Pietzsch for help on the light-sheet imaging and reconstruction of the multiview datasets. Funding: We acknowledge funding from the Leibniz prize of P.F. running under DFG contract number FR2190/4-1. Author contributions: S.E. and J.W.C.D. designed the study. S.E., B.S., A.W., and K.L. performed the cell culture experiments. S.E. and A.W. performed the light-sheet imaging of the tissues. S.E. and B.S. performed the confocal imaging and live-cell imaging. S.E., C.J., and B.S. analyzed the images. S.E., P.F., and J.W.C.D. interpreted the data. F.D.F. and P.F. developed the membrane mechanics model. S.E. and J.W.C.D. performed the Surface Evolver simulations. S.E. and J.W.C.D. wrote the manuscript. All authors edited the manuscript and gave final approval for publication. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/9/eaav9394/DC1
Fig. S1. Principle of the scaffold preparation procedure.
Fig. S2. Equilibrium surfaces of axially symmetric configurations.
Fig. S3. Experimental measurements compared to theoretical predictions of a liquid interface.
Fig. S4. Experimental results of blebbistatin and TGF-β1 treatments.
Fig. S5. Membrane theory of thin shells of revolution applied to CB surfaces.
Fig. S6. Asymptotic directions on hyperboloids compared to CB surfaces.
Fig. S7. Method of quantifying actin fiber angles and asymptotics on CB surfaces.
Fig. S8. Example of actin fiber-angle direction analysis and local correlations.
Fig. S9. Actin fiber angle distributions on the CB surfaces.
Fig. S10. Time evolution of actin fiber angle distributions on CB.
Movie S1. 3D LSFM image of tissue grown on a capillary bridge surface.
REFERENCES AND NOTES
- 1.Lecuit T., Lenne P.-F., Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 8, 633–644 (2007). [DOI] [PubMed] [Google Scholar]
- 2.Friedl P., Gilmour D., Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 10, 445–457 (2009). [DOI] [PubMed] [Google Scholar]
- 3.Mongera A., Rowghanian P., Gustafson H. J., Shelton E., Kealhofer D. A., Carn E. K., Serwane F., Lucio A. A., Giammona J., Campàs O., A fluid-to-solid jamming transition underlies vertebrate body axis elongation. Nature 561, 401–405 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.He B., Doubrovinski K., Polyakov O., Wieschaus E., Apical constriction drives tissue-scale hydrodynamic flow to mediate cell elongation. Nature 508, 392–396 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schötz E.-M., Lanio M., Talbot J. A., Manning M. L., Glassy dynamics in three-dimensional embryonic tissues. J. R. Soc. Interface 10, 20130726 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Foty R. A., Steinberg M. S., The differential adhesion hypothesis: A direct evaluation. Dev. Biol. 278, 255–263 (2005). [DOI] [PubMed] [Google Scholar]
- 7.Ophir J., Céspedes I., Ponnekanti H., Yazdi Y., Li X., Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrason. Imaging 13, 111–134 (2016). [DOI] [PubMed] [Google Scholar]
- 8.Rumpler M., Woesz A., Dunlop J. W., van Dongen J. T., Fratzl P., The effect of geometry on three-dimensional tissue growth. J. R. Soc. Interface 5, 1173–1180 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bidan C. M., Kommareddy K. P., Rumpler M., Kollmannsberger P., Bréchet Y. J. M., Fratzl P., Dunlop J. W. C., How linear tension converts to curvature: Geometric control of bone tissue growth. PLOS ONE 7, e36336 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.D. Langbein, Capillary Surfaces: Shape—Stability—Dynamics, in Particular Under Weightlesness (Springer, 2002). [Google Scholar]
- 11.D’A.W. Thompson, On Growth and Form (Cambridge Univ. Press, 1992). [Google Scholar]
- 12.Cukierman E., Pankov R., Stevens D. R., Yamada K. M., Taking cell-matrix adhesions to the third dimension. Science 294, 1708–1712 (2001). [DOI] [PubMed] [Google Scholar]
- 13.Harunaga J. S., Yamada K. M., Cell-matrix adhesions in 3D. Matrix Biol. 30, 363–368 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Foolen J., Yamashita T., Kollmannsberger P., Shaping tissues by balancing active forces and geometric constraints. J. Phys. D. Appl. Phys. 49, 053001 (2016). [Google Scholar]
- 15.Baker B. M., Chen C. S., Deconstructing the third dimension—How 3D culture microenvironments alter cellular cues. J. Cell Sci. 125, 3015–3024 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen B., Ji B. H., Gao H. J., Modeling active mechanosensing in cell-matrix interactions. Annu. Rev. Biophys. 44, 1–32 (2015). [DOI] [PubMed] [Google Scholar]
- 17.Nelson C. M., Jean R. P., Tan J. L., Liu W. F., Sniadecki N. J., Spector A. A., Chen C. S., Emergent patterns of growth controlled by multicellular form and mechanics. Proc. Natl. Acad. Sci. U.S.A. 102, 11594–11599 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ruiz S. A., Chen C. S., Emergence of patterned stem cell differentiation within multicellular structures. Stem Cells 26, 2921–2927 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yamashita T., Kollmannsberger P., Mawatari K., Kitamori T., Vogel V., Cell sheet mechanics: How geometrical constraints induce the detachment of cell sheets from concave surfaces. Acta Biomater. 45, 85–97 (2016). [DOI] [PubMed] [Google Scholar]
- 20.Kollmannsberger P., Bidan C. M., Dunlop J. W. C., Fratzl P., Vogel V., Tensile forces drive a reversible fibroblast-to-myofibroblast transition during tissue growth in engineered clefts. Sci. Adv. 4, eaao4881 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Knychala J., Bouropoulos N., Catt C. J., Katsamenis O. L., Please C. P., Sengers B. G., Pore geometry regulates early stage human bone marrow cell tissue formation and organisation. Ann. Biomed. Eng. 41, 917–930 (2013). [DOI] [PubMed] [Google Scholar]
- 22.Paris M., Götz A., Hettrich I., Bidan C. M., Dunlop J. W. C., Razi H., Zizak I., Hutmacher D. W., Fratzl P., Duda G. N., Wagermaier W., Cipitria A., Scaffold curvature-mediated novel biomineralization process originates a continuous soft tissue-to-bone interface. Acta Biomater. 60, 64–80 (2017). [DOI] [PubMed] [Google Scholar]
- 23.Wang L., McCarthy T. J., Capillary-bridge–derived particles with negative Gaussian curvature. Proc. Natl. Acad. Sci. U.S.A. 112, 2664–2669 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Herklotz M., Prewitz M. C., Bidan C. M., Dunlop J. W. C., Fratzl P., Werner C., Availability of extracellular matrix biopolymers and differentiation state of human mesenchymal stem cells determine tissue-like growth in vitro. Biomaterials 60, 121–129 (2015). [DOI] [PubMed] [Google Scholar]
- 25.Brakke K. A., The Surface Evolver. Exp. Math. 1, 141–165 (1992). [Google Scholar]
- 26.Pérez-González C., Alert R., Blanch-Mercader C., Gómez-González M., Kolodziej T., Bazellières E., Casademunt J., Trepat X., Active wetting of epithelial tissues. Nat. Phys. 15, 79 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.R. B. Martin, D. Burr, N. A. Sharkey, Skeletal Tissue Mechanics (Springer, 2015). [Google Scholar]
- 28.Duclos G., Erlenkämper C., Joanny J.-F., Silberzan P., Topological defects in confined populations of spindle-shaped cells. Nat. Phys. 13, 58–62 (2017). [Google Scholar]
- 29.Bade N. D., Xu T., Kamien R. D., Assoian R. K., Stebe K. J., Gaussian curvature directs stress fiber orientation and cell migration. Biophys. J. 114, 1467–1476 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bidan C. M., Kollmannsberger P., Gering V., Ehrig S., Joly P., Petersen A., Vogel V., Fratzl P., Dunlop J. W. C., Gradual conversion of cellular stress patterns into pre-stressed matrix architecture during in vitro tissue growth. J. R. Soc. Interface 13, 20160136 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wan L. Q., Ronaldson K., Park M., Taylor G., Zhang Y., Gimble J. M., Vunjak-Novakovic G., Micropatterned mammalian cells exhibit phenotype-specific left-right asymmetry. Proc. Natl. Acad. Sci. U.S.A. 108, 12295–12300 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wagermaier W., Gupta H. S., Gourrier A., Burghammer M., Roschger P., Fratzl P., Spiral twisting of fiber orientation inside bone lamellae. Biointerphases 1, 1–5 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Giraud-Guille M.-M., Belamie E., Mosser G., Helary C., Gobeaux F., Vigier S., Liquid crystalline properties of type I collagen: Perspectives in tissue morphogenesis. C. R. Chim. 11, 245–252 (2008). [Google Scholar]
- 34.Kocica M. J., Corno A. F., Carreras-Costa F., Ballester-Rodes M., Moghbel M. C., Cueva C. N., Lackovic V., Kanjuh V. I., Torrent-Guasp F., The helical ventricular myocardial band: Global, three-dimensional, functional architecture of the ventricular myocardium. Eur. J. Cardiothorac. Surg. 29 (suppl. 1), S21–S40 (2006). [DOI] [PubMed] [Google Scholar]
- 35.S. Hyde, Z. Blum, T. Landh, S. Lidin, B.W. Ninham, S. Andersson, K. Larsson, The Language of Shape: The Role of Curvature in Condensed Matter: Physics, Chemistry and Biology (Elsevier, 1996). [Google Scholar]
- 36.Jinnai H., Nishikawa Y., Ito M., Smith S. D., Agard D. A., Spontak R. J., Topological similarity of sponge-like bicontinuous morphologies differing in length scale. Adv. Mater. 14, 1615–1618 (2002). [Google Scholar]
- 37.Wilts B. D., Apeleo Zubiri B., Klatt M. A., Butz B., Fischer M. G., Kelly S. T., Spiecker E., Steiner U., Schröder-Turk G. E., Butterfly gyroid nanostructures as a time-frozen glimpse of intracellular membrane development. Sci. Adv. 3, e1603119 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dee G. T., Sauer B. B., The molecular weight and temperature dependence of polymer surface tension: Comparison of experiment with interface gradient theory. J. Colloid Interface Sci. 152, 85–103 (1992). [Google Scholar]
- 39.Félix A. S. C., Santiago-Alvarado A., Iturbide-Jiménez F., Licona-Morán B., Physical-chemical properties of PDMS samples used in tunable lenses. Intl. J. Eng. Sci. Innov. Tech. 3, 563–570 (2014). [Google Scholar]
- 40.Tan W., Desai T. A., Layer-by-layer microfluidics for biomimetic three-dimensional structures. Biomaterials 25, 1355–1364 (2004). [DOI] [PubMed] [Google Scholar]
- 41.K. A. Brakke, Surface Evolver 2.70 (2013).
- 42.Gillette R. D., Dyson D. C., Stability of fluid interfaces of revolution between equal solid circular plates. Chem. Eng. J. 2, 44–54 (1971). [Google Scholar]
- 43.M. H. Jawad, Membrane theory of shells of revolution, in Theory and Design of Plate and Shell Structures, M. H. Jawad, Ed. (Springer, 1994). pp. 163–192. [Google Scholar]
- 44.R. McNeel, Rhinoceros 5.0 (Robert McNeel & Associates, 2013).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
http://advances.sciencemag.org/cgi/content/full/5/9/eaav9394/DC1
Download PDF
Movie S1
Surface tension determines tisue shape and growth kinetics
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/9/eaav9394/DC1
Fig. S1. Principle of the scaffold preparation procedure.
Fig. S2. Equilibrium surfaces of axially symmetric configurations.
Fig. S3. Experimental measurements compared to theoretical predictions of a liquid interface.
Fig. S4. Experimental results of blebbistatin and TGF-β1 treatments.
Fig. S5. Membrane theory of thin shells of revolution applied to CB surfaces.
Fig. S6. Asymptotic directions on hyperboloids compared to CB surfaces.
Fig. S7. Method of quantifying actin fiber angles and asymptotics on CB surfaces.
Fig. S8. Example of actin fiber-angle direction analysis and local correlations.
Fig. S9. Actin fiber angle distributions on the CB surfaces.
Fig. S10. Time evolution of actin fiber angle distributions on CB.
Movie S1. 3D LSFM image of tissue grown on a capillary bridge surface.