Quantitative Relationship between Transmitter Release and Calcium Current at the Calyx of Held Synapse (original) (raw)
Abstract
A newly developed deconvolution method (Neher and Sakaba, 2001) allowed us to resolve the time course of neurotransmitter release at the calyx of Held synapse and to quantify some basic aspects of transmitter release. First, we identified a readily releasable pool (RRP) of synaptic vesicles. We found that the size of the RRP, when tested with trains of strong stimuli, was constant regardless of the exact stimulus patterns, if stimuli were confined to a time interval of ∼60 msec. For longer-lasting stimulus patterns, recruitment of new vesicles to the RRP made a substantial contribution to the total release. Second, the cooperativity of transmitter release as a function of Ca2+ current was estimated to be 3–4, which confirmed previous results (Borst and Sakmann, 1999; Wu et al., 1999). Third, an initial small Ca2+ influx increased the efficiency of Ca2+ currents in subsequent transmitter release. This type of facilitation was blocked by a high concentration of EGTA (0.5 mm). Fourth, the release rates of synaptic vesicles at this synapse turned out to be heterogeneous: once a highly Ca2+-sensitive population of vesicles was consumed, the remaining vesicles released at lower rates. These components of release were more clearly separated in the presence of 0.5 mm EGTA, which prevented the buildup of residual Ca2+. Conversely, raising the extracellular Ca2+ concentration facilitated the slower population such that its release characteristics became more similar to those of the faster population under standard conditions. Heterogeneous release probabilities are expected to support the maintenance of synaptic transmission during high-frequency stimulation.
Keywords: transmitter release, synaptic depression, facilitation, release probability, vesicle pool, the calyx of Held
Knowledge of the kinetics of transmitter release and its dependence on Ca2+ influx is important for elucidating the molecular mechanisms mediating exocytosis from presynaptic terminals. In particular, short-term plastic changes, such as synaptic facilitation and depression, are likely to have presynaptic components, the quantification of which require accurate knowledge of release rates. Until now, the time course of transmitter release in most mammalian synapses has been assayed mainly by analyzing postsynaptic responses. In the neuromuscular junction, deconvolution of the EPSCs with the miniature EPSC (mEPSC) gives an accurate estimate of the time course of transmitter release (van der Kloot 1988a,b), because the released quanta do not interact with each other (Hartzell et al., 1975;Magleby and Pallotta, 1981). However, this assumption cannot always be made in central synapses. Postsynaptic factors, such as desensitization (Trussell et al., 1993; Otis et al., 1996) or saturation of receptors (Jonas et al., 1993; Tang et al., 1994; Auger et al., 1998), and delayed clearance of the released transmitter from the synaptic cleft (Barbour et al., 1994; Mennerick and Zorumski, 1995; Silver et al., 1996) can also contribute to the time course of the EPSC. All of these mechanisms prevent accurate characterization of the presynaptic factors mediating the EPSC. Thus, deconvolution has so far been applied to only a limited number of central synapses (Borges et al., 1995; Diamond and Jahr, 1995).
To separate the presynaptic and postsynaptic factors that determine the time course of the EPSC, we have developed a novel type of deconvolution (Neher and Sakaba, 2001). In this method, we modeled the residual current component caused by the delayed clearance of glutamate from the synaptic cleft and incorporated this current into the deconvolution algorithm. The validity of the method was tested using fluctuation analysis and is described in detail in a recent paper (Neher and Sakaba, 2001).
At the calyx of Held synapse, an axosomatic synapse in the brainstem, it is possible to clamp the presynaptic terminal and the postsynaptic target simultaneously (Borst et al., 1995; Takahashi et al., 1996), allowing precise timing and quantification of the presynaptic Ca2+ influx, as well as the measurement of EPSCs at high time resolution. Basic aspects of transmitter release, such as the cooperativity of transmitter release and its dependence on extracellular Ca2+ concentration (Borst and Sakmann, 1996, 1999a; Takahashi et al., 1996; Wu et al., 1999), as well as the size of the readily releasable pool (RRP) of synaptic vesicles (Schneggenburger et al., 1999; Wu and Borst, 1999), have already been investigated at this synapse. However, possible postsynaptic factors affecting the EPSCs were not taken into account. Using our new deconvolution method, we have been able to analyze the effects of these postsynaptic mechanisms and found that both receptor desensitization and saturation can readily occur during intense stimulation protocols. However, in the presence of cyclothiazide (CTZ) and kynurenic acid (Kyn), both effects are reduced to the point that they are no longer a serious cause of error in deconvolution (Neher and Sakaba, 2001). Using these drugs, we now present data which show that the size of the RRP is constant regardless of the stimulus patterns used and also much larger than previously estimated. Additionally, we find that the release probabilities of synaptic vesicles are heterogeneous. Possible mechanisms and biological implications of these findings are discussed.
MATERIALS AND METHODS
Presynaptic and postsynaptic recordings at the calyx of Held were performed in slice preparations of the rat brainstem at room temperature (21–24°C) as described elsewhere (Neher and Sakaba, 2001). Briefly, a slice was transferred to the recording chamber and perfused continuously with normal saline at a rate of ∼1 ml/min. Normal saline contained (in mm): NaCl 125, KCl 2.5, CaCl2 2.0, MgCl2, 1.0, glucose 25, NaHCO3 1.25, ascorbic acid 0.4, myo-inositol 3, and Na-pyruvate 2, pH 7.3–7.4, 320 mOsm, and was bubbled continuously with 95% O2 and 5% CO2.
The presynaptic and postsynaptic compartments were simultaneously clamped at a holding potential of −80 mV (unless noted otherwise). The presynaptic pipette (4–7 MΩ) was filled with a solution containing (in mm): Cs-gluconate 125–130, TEA-Cl 20, HEPES 10, Na2 phosphocreatine 5, MgATP 4, GTP 0.3, BAPTA 0.05, pH 7.2, 310 mOsm. In some experiments the concentration of BAPTA was either increased to 0.2 mm or replaced by EGTA (0.05 or 0.5 mm). The postsynaptic pipette (2–4 MΩ) was filled with the same solution as the presynaptic pipette, except that BAPTA was replaced by 5 mm EGTA.
During recordings, 0.5–1 μm TTX, 10 mmTEA-Cl, and 50 μmd-2-amino-4-phosphonobutyric acid (d-AP5) were added to the normal saline to isolate the presynaptic calcium current and to block NMDA receptors. In some cases, 0.1 mm3,4-diaminopyridine was also added to block the presynaptic K+ current. Bicuculine (10 μm) and strychnine (2 μm) were added in some recordings to block possible inhibitory input. To vary the extracellular calcium concentration, the CaCl2concentration of the normal saline was increased to 10 mm. In some recordings, 2 or 10 mm CaCl2was added to a solution containing (in mm): NaCl 150, KCl 2.5, HEPES 10, and glucose 10, pH 7.3–7.4, 320 mOsm. In most experiments, Kyn (1 mm) and CTZ (100 μm) were added, because it was shown that desensitization and saturation of postsynaptic receptors can be avoided only in the presence of these drugs (Neher and Sakaba, 2001). CTZ, Kyn,d-AP5, and 2,3-dioxo-6-nitro-1,2,3,4,-tetrahydrobenzoquinoxaline-7-sulfonamide (NBQX) were purchased from Tocris (Köln, Germany). Bicuculine, strychnine, 3,4-diaminopyridine, and TEA were from Sigma (Deisenhofen, Germany). TTX was from Alamone Labs (Jerusalem, Israel).
Both presynaptic and postsynaptic cells were whole-cell-clamped with an EPC9/2 amplifier controlled by the Pulse program (HEKA-Electronik, Lambrecht, Germany) to a holding potential of −80 mV. Currents were low-pass-filtered at 2.9 or 6 kHz and stored at 10 or 20 kHz. The presynaptic series resistance (_R_s; 8–35 MΩ, typically 15 MΩ) was compensated 30–70%. Subtraction of the presynaptic capacitive current was made with the P/5 protocol or by scaling the capacitive current by a small voltage pulse. This correction was applied for the calculation of plateau inward currents during depolarizations. However, the original traces in the figures show uncorrected records. Presynaptic leak currents of >200 pA typically caused rundown of the postsynaptic response; therefore, recordings from cells with such leakage were not used. The interval between the two stimuli was 20–30 sec. The postsynaptic series resistance (3–10 MΩ, typically 5 MΩ) was compensated so that the uncompensated series resistance was ∼2–3 MΩ. Residual resistance was compensated off-line by correcting for the deviation from the holding potential (=_R_s ×_I_EPSC). Postsynaptic leak currents were typically 50–100 pA. Recordings were stopped once the uncompensated postsynaptic _R_s became >10 MΩ or the postsynaptic leak current was >300 pA. Most of the data that had postsynaptic _R_s of >8 MΩ were rejected later during analysis because power spectra showed that the high-frequency signal is reduced by high_R_s.
Deconvolution of postsynaptic current records was performed as described by Neher and Sakaba (2001). This procedure calculates release rates ξ(t) in vesicles released per millisecond. A first-order estimate of the total size of the RRP can be obtained by integrating the release rate between the beginning of a stimulus protocol and the end of a depleting stimulus (all of our stimulus protocols are concluded by such depleting stimuli; see below). However, this integral includes vesicles that have been newly recruited to the RRP while the stimulus protocol proceeds. To correct for this effect, we applied an iterative procedure based on the simplest possible pool model, which is a homogeneous pool of_N_t vesicles, when completely filled, and recovering exponentially with a time constant τ, when fully or partially depleted. Designating n(t) as the pool size at a given time t, this model can be represented by the rate equation:
| dn(t)dt=−ξ(t)+[Nt−n(t)]/τ. | Equation 1 |
|---|
This can be integrated to yield:
| n(t)=Nt1+tτ−∫0tξ(t′)dt′−1τ∫0tn(t′)dt′. | Equation 2 |
|---|
As initial guesses _N_t,0 for_N_t we use:
| Nt,0=∫0t1ξ(t)dt, | Equation 3 |
|---|
where t_1 is the time at which the depleting pulse ends. The initial value_n_0(t) for_n(t) is calculated according to:
| n0(t)=Nt,0−∫0tξ(t′)dt′. | Equation 4 |
|---|
With these values inserted into the right side of Equation 2, we obtain an improved estimate_n_1(t), from which we calculate an improved estimate for _N_t, according to:
| Nt,1=0.7·(n1(0)−n1(t))+0.3Nt,0 | Equation 5 |
|---|
Here, we calculate a weighted average of new and previous estimates to avoid oscillation in the iteration. Repeating these steps iteratively two to five times results in stable values for_N_t,v and_n_v(t), which are then taken as the initial pool size, and the number of remaining vesicles at a given time t, respectively. The quantity “release rate per vesicle”, ξpv (see below), was calculated according to:
| ξpv(t)=ξ(t)/nv(t), | Equation 6 |
|---|
with _n_v(t) calculated according to Equation 2 using a stable value of_N_t,v (in place of_N_t).
This procedure clearly is an oversimplification because it has been shown that recovery of the pool is not described by a single exponential (Wu and Borst, 1999). However, all of our protocols are short (<120 msec) relative to the fast time constant of recovery of Wu and Borst (1999) (200–300 msec). Therefore, it is only the initial rate of recovery that is of relevance for the calculation. We represent this, for simplicity, by a single time constant.
RESULTS
Presynaptic effects of CTZ
In our experiments, we used CTZ to block desensitization of postsynaptic AMPA receptors and to slow the decay of EPSCs. However, it has been suggested that CTZ may act presynaptically to enhance transmitter release (Barnes-Davies and Forsythe, 1995; Diamond and Jahr, 1995; Isaacson and Walmsley, 1996; Bellingham and Walmsley, 1999). In a preceding paper, we have shown that AMPA receptors desensitize strongly during synaptic transmission in the absence of CTZ (Neher and Sakaba, 2001). Therefore, the enhancement of the synaptic response seen in the presence of CTZ is most likely caused by block of the desensitization of postsynaptic receptors rather than an increase in transmitter release.
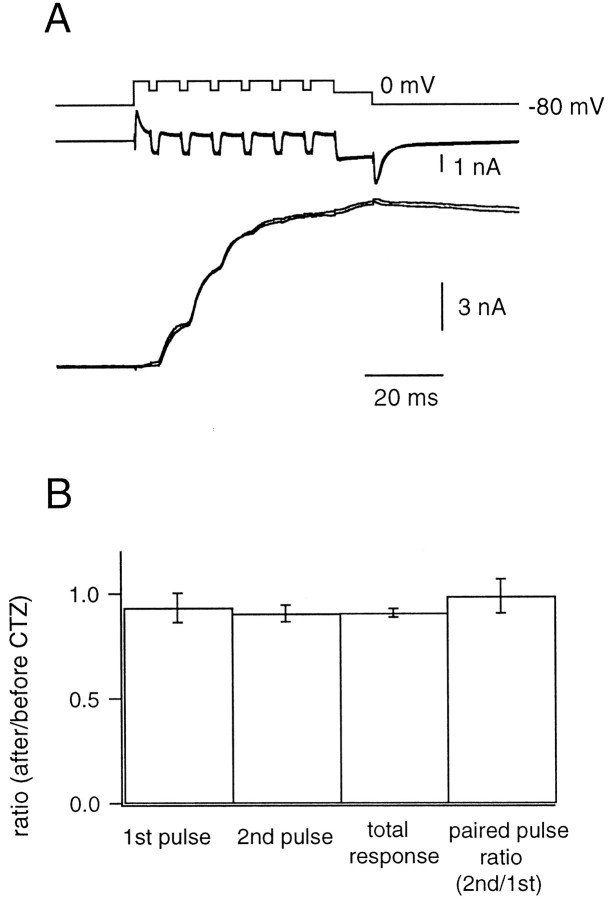
To further explore this question, we also examined the effects of CTZ on NMDA receptor-mediated EPSCs (NMDA EPSCs), which have been used for testing the presynaptic effects of this drug (Trussell et al., 1993;Diamond and Jahr, 1995; Bellingham and Walmsley, 1999). The NMDA EPSC was isolated by application of 1 μm NBQX and 10 μm glycine, whereas the postsynaptic neuron was held at either −40 or +60 mV. Strychnine (2 μm) was also applied to avoid responses to glycine. Trains of pulses (depolarization to 20 mV for 2 msec with an interpulse interval of 6 msec) were applied to the presynaptic terminal. Responses to pulses did not change significantly after the addition of CTZ (100 μm) (Fig.1A,B). Specifically, the EPSC amplitude in the presence of CTZ was ∼90% of the control EPSC amplitude for both the first (0.93 ± 0.07) and second (0.91 ± 0.04) pulse (n = 5 cell pairs). Also, the paired-pulse ratio of the EPSCs (0.99 ± 0.08) did not change substantially in the presence of CTZ (Fig.1B). Therefore, we found no evidence for presynaptic effects mediated by CTZ in our experimental conditions. However, we cannot entirely exclude the possibility that CTZ modulates transmitter release under current-clamp conditions, for example, by modulating ion channels, instead of modulating the release machinery.
Fig. 1.
The effect of cyclothiazide (CTZ) on the NMDA EPSC. A, The presynaptic terminal was depolarized from −80 to +80 mV and repetitively shifted back to +20 mV every 8 msec for 2 msec. After repeating this stimulus six times, the terminal was held at 0 mV for 10 msec (_V_Pre). The Ca2+currents (middle) and the NMDA EPSCs (bottom) before and after the application of CTZ (100 μm) were superimposed. The NMDA EPSC was isolated by application of 1 μm NBQX and 10 μm glycine, and the postsynaptic neuron was held at +60 mV. Strychnine (2 μm) was also applied to avoid responses to glycine.B, Left to right, The EPSC amplitude evoked by the first pulse (1st pulse), the second pulse (2nd pulse), the EPSC amplitude achieved at the end of the stimulus protocol (total response), and the paired-pulse ratio [ratio between the second pulse and the first pulse (2nd/1st)]. In all cases, quantities indicated were measured both before and after the application of CTZ. Ratios of these values before and after the application of CTZ are plotted (n = 5 cell pairs).
Transmitter release rates estimated from deconvolution
In the presence of CTZ, a large current component of the EPSC (the residual current component) arises from the delayed clearance of glutamate from the synaptic cleft. Therefore, simple deconvolution of the EPSC with the mEPSC overestimates release rates. Thus, the residual current component must be subtracted from the EPSC before deconvolution can be performed. Also, Kyn, a fast competitive glutamate antagonist, must be included in the bath solution to avoid receptor saturation and clamp errors. To calculate the residual current, we used a simple model of glutamate diffusion [for a detailed description, see Neher and Sakaba (2001)]. The protocol shown in Figure2A, referred to as the “fitting protocol, ” was used to determine the free parameters of this model (n, the exponent of the power law of glutamate channel activation; _r_D, the diffusional distance; and _n_D, the exponent of the diffusion law). In the fitting protocol, the presynaptic terminal was depolarized from −80 to +70 mV to activate Ca2+ channels maximally. At this potential there was almost no Ca2+ influx, because the driving force of Ca2+ was very low. From +70 mV the voltage of the terminal was shifted to 0 mV several times. Durations of these repolarizations were adjusted so that the resulting Ca2+ influx evoked EPSCs that varied several-fold in amplitude. The EPSCs decayed during episodes when the presynaptic terminal was held at +70 mV. The rate of quantal release calculated by variance analysis was <10 msec−1during such decay phases of EPSCs (Neher and Sakaba, 2001), suggesting low rates of asynchronous release. Because the EPSC decay is largely shaped by the delayed clearance of glutamate and not by asynchronous release, we could set parameters of the glutamate diffusion model from the decay phases of the EPSCs (Fig. 2A, dotted line close to the EPSC trace). Parameters of the diffusion model were determined for each cell pair using a fitting protocol like that described in Figure 2A. Then, deconvolution was performed after subtracting the residual current component (Fig.2A). Once parameters were determined, they were used for other traces in a given cell pair.
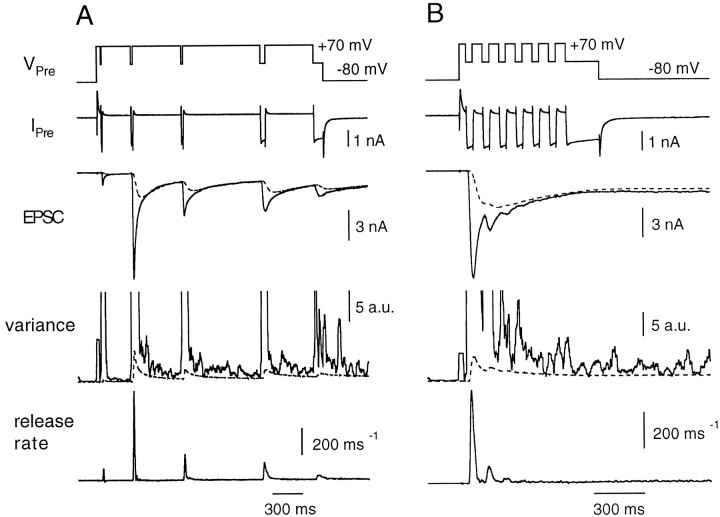
Fig. 2.
The deconvolution method to estimate quantal release rates at the calyx of Held. A, The fitting protocol to determine parameters of the glutamate diffusion model. The presynaptic voltage (V Pre) was shifted from −80 to +70 mV and then repolarized to 0 mV (1–10 msec in duration) several times. IPre denotes presynaptic voltage-clamp current, which represents mainly Ca2+ current, not corrected for leak and capacitance current. Durations of these repolarizations were adjusted so that the size of EPSCs varied several-fold. Filtered variance (variance, solid line) was used to estimate release rates during the EPSC decay (Neher and Sakaba, 2001). The dotted line in the variance trace indicates an estimate of AMPA receptor channel noise (Neher and Sakaba, 2001). The difference between the total variance and channel noise should arise from fluctuations associated with quantal release. Parameters of the glutamte diffusion model, which accounts for the residual current caused by delayed clearance of glutamate (Neher and Sakaba, 2001), were determined from EPSC decay phases. After subtracting the residual current component (dotted line on the EPSC trace) from the total EPSCs, release rates (release rate, bottom) were calculated by deconvolution of the remaining EPSC with the mEPSC. The presynaptic patch pipette contained 0.05 mm BAPTA. B, Release rates during trains of pulses. The presynaptic terminal was depolarized from −80 to +70 mV and repetitively shifted back to −5 mV every 10 msec for 4 msec. After repeating this stimulus six times, the terminal was held at −5 mV for 20 msec to deplete the RRP. Release rates were calculated after subtracting the residual current component (dotted line in the EPSC trace) from the total EPSC. Variance associated with EPSCs and channel variance (dotted line) are also shown. The data were obtained from the same cell pair as shown in A.
To investigate the kinetics of transmitter release, we applied trains of pulses as shown in Figure 2B. The presynaptic terminal was depolarized to +70 mV to activate Ca2+ channels fully while keeping Ca2+ influx minimal. The terminal was then repetitively shifted back to a fixed potential every 10 msec (in the case of Fig. 2B, to −5 mV) for 4 msec to allow a finite amount of Ca2+ influx. After six such stimuli, the terminal was held at −5 mV for 20 msec to deplete completely the RRP of synaptic vesicles (hence, the name “depleting pulse”). We did not see a significant inactivation of the presynaptic Ca2+ current in the protocol that we used (Forsythe et al., 1998; but see Borst and Sakmann, 1999b) (Fig.2B, _I_pre). Compared with the first pulse, the Ca2+ current amplitudes during the second and third pulses were 100 ± 1% and 97 ± 1%, respectively. We did not see facilitation of the Ca2+ current as has been reported previously (Borst and Sakmann, 1998; Cuttle et al., 1998). This is because Ca2+ channels were activated maximally in our protocols, whereas facilitation of Ca2+ current was seen only when Ca2+ channels were partially activated (Borst and Sakmann, 1998; Cuttle et al., 1998).
The release rate was calculated by deconvolution as described above (Fig. 2B). It increased during the first episode of presynaptic Ca2+ influx and decreased immediately after cessation of the Ca2+influx. Both the EPSC and the peak release rate were depressed during successive stimuli, suggesting that the first pulse released most of the RRP. Furthermore, the depleting pulse at the end of the protocol evoked almost no release (Fig. 2B). Variance analysis also indicated that the release rate at the end of a depleting pulse is quite low (∼6 msec−1) (Neher and Sakaba, 2001).
A readily releasable pool of synaptic vesicles at the calyx of Held synapse
Using this deconvolution method, we were also able to estimate the size of the RRP of vesicles. Our expectation is that a constant number of vesicles should be released by a sufficiently strong stimulus, regardless of the stimulus pattern, if pool depletion is the main mechanism of synaptic depression (Neher, 1998a; but see Hsu et al., 1996). A protocol similar to that of Figure 2B was used, except that the magnitude of the repolarization was varied in each train of pulses to elicit varying amplitudes of Ca2+ current. Because the terminal was depolarized first to +70 mV, the half-time of the Ca2+ current rise during repolarization was the same regardless of the level of repolarization. At the end of all stimulus protcols, the presynaptic terminal was held at −5 mV for 20 msec to deplete the RRP completely (Fig.3A,VPre).
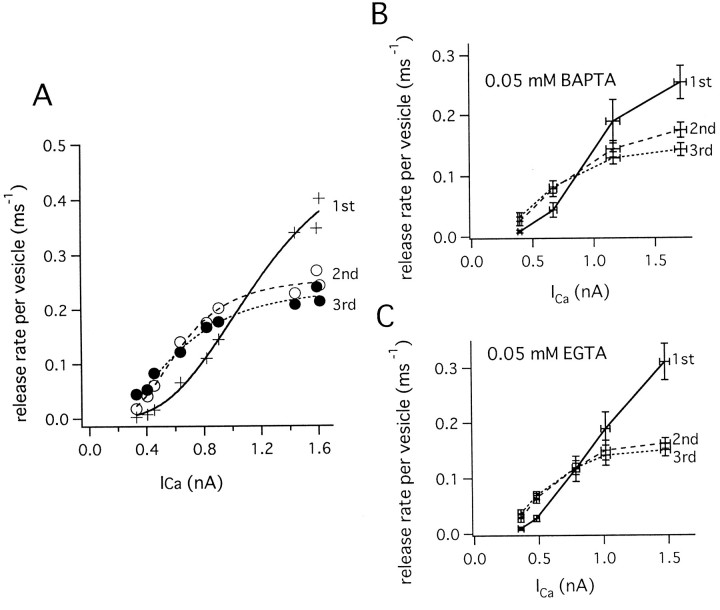
Fig. 3.
Relationship between release rate and Ca2+ influx. A, A protocol similar to that described in Figure 2B was used, except that pulse durations were kept constant and the magnitude of repolarization was varied in each train of pulses, thereby varying amounts of Ca2+ influx. Four sweeps were superimposed. Different colors represent the different sweeps in the traces for V Pre,IPre, EPSC, and the_Release Rate_. The data were obtained from the same cell pair as shown in Figure 2. Details of the presynaptic inward currents evoked by the first pulse in each record are shown in the_inset_ between the two bottom-most traces. These records have not been corrected for leak and capacitive transients (see Materials and Methods). B, The number of vesicles released during the stimulation protocol was calculated by integrating the release rate. The release rate was integrated from the end of the depleting pulse to the beginning of the protocol. Therefore, this figure shows the number of remaining vesicles. We assumed that new synaptic vesicles were recruited to the RRP with a time constant of 1 sec, calculating the integral according to Equation 2. The individual traces correspond to those of A, using the same_color code. C_, The release rates per vesicle during the first three pulses, calculated according to Equation5, are shown. The traces correspond to those of_A_, using the same colors.
In cases of larger Ca2+ influxes (for example, the green trace in Fig. 3A), the peak release rate during the initial stimulus was large, and the release rate was depressed during subsequent stimuli. In contrast, during smaller initial Ca2+ influxes (for example, the red trace in Fig. 3A), the peak release rate during the initial stimulus was very small, and the release rate was facilitated by subsequent stimuli (Fig.3A). For all stimulus patterns, the release rate declined to a low value at the end of the depleting pulse. The number of vesicles released during stimulation was calculated by integrating the release rate and considering also partial pool refilling during the stimulus, as described in Materials and Methods (Fig. 3B). A constant number of vesicles (∼2000) were released during all stimulus patterns. Although the number varied among different cell pairs (from 800 to 4400), the number was almost constant within a single cell pair. The average number of releasable vesicles from 11 cell pairs was 2408 ± 309.
The above estimation assumes that recovery of the RRP of synaptic vesicles occurs with a time constant of 1 sec (see Materials and Methods). This value comes from experiments in which double depolarizations to −10 mV for 20 msec were applied to the presynaptic terminal with an interpulse interval of 500 msec. Each pulse was strong enough to deplete completely the RRP of synaptic vesicles. The number of vesicles released by the second pulse was 47% (41–49%;n = 3 cell pairs) of the number released by the first pulse. Thus, the entire RRP of synaptic vesicles should be refilled in ∼1 sec assuming that refilling proceeds at a constant rate for all vesicles. However, it has been shown that a subset of vesicles of the RRP at the calyx synapse recovers faster (Wu and Borst 1999). Therefore, we also estimated the size of the RRP assuming a much faster recovery time constant. To determine this faster recovery time constant, we examined the release rate at the end of the depleting pulse and during a short time interval after the depleting pulse. We found that the release rate approached values of 10 msec−1(9.8 ± 1.9 msec−1;n = 11 cell pairs; see also Fig. 5A). This value should reflect the rate at which (after depletion) new vesicles are recruited to the RRP and immediately released, because the Ca2+ concentrations after strong depolarization are expected to be high (Wu and Borst, 1999). Integrating this rate for individual experiments yields recovery time constants between 200 and 1000 msec (typically 200−400 msec), similar to values found in a previous study (Wu and Borst, 1999). Using 200−400 msec as a time constant, we recalculated the size of the RRP to be 2246 ± 303 vesicles (n = 11 cell pairs) with pool size estimates from individual traces fluctuating typically by ±10% around the mean pool size of a given cell pair. Thus, the effect of pool recovery turned out to be minor, probably because the stimulation protocol was relatively short (<100 msec) compared with the recovery time constant. For the following analyses, we assumed fast recovery (τ = 200−400 msec). However, the results did not differ significantly when the recovery time constant was assumed to be 1 sec.
Fig. 5.
The effect of 0.5 mm EGTA on release rates per vesicle. A, The same protocols as described in Figure 3 were used. However, the presynaptic patch pipette contained 0.5 mm EGTA. Release rates observed during the depleting pulse are shown at two different magnifications. Note that the Ca2+ tail current at the end of the depleting pulse (indicated by a short artifact in the inset) does not lead to any changes in release rate. B, The relationship between the peak release rate per vesicle and the amplitude of the Ca2+ current. The data are from the cell pair shown in A. The peak values of release rate per vesicle during the first (continuous line), second (broken line), and third (dotted line) pulses were plotted against the amplitude of Ca2+ current. First pulses could be fitted with a power relationship (Eq. 8) with_n_ = 2.43. Second and third pulses were fitted with a Hill function (second pulse: ξmax = 0.12 msec−1; K = 739 pA; n = 3.42; third pulse: ξmax = 0.13 msec−1; K = 204 pA; n = 0.916). C, Summary of the relationship between the peak release rate per vesicle during the first (continuous line), second (broken line), and third (dotted line) pulses and the amplitude of Ca2+ current. The presynaptic patch pipette contained 0.5 mm EGTA (n = 4 cell pairs).
The pool size that we estimated was larger than previous estimates (600–800 vesicles) (Schneggenburger et al., 1999; Wu and Borst, 1999). These previous studies assumed that the size of the mEPSC was constant under the experimental conditions examined. However, this assumption is usually not warranted at the calyx of Held, because postsynaptic AMPA receptors desensitize in the absence of CTZ and saturate in the presence of CTZ, unless a fast blocker of glutamate binding such as Kyn is added (Neher and Sakaba, 2001). Also, an appreciable fraction of release may occur desynchronized during bursts of strong stimuli, such that the cumulative amplitude of EPSCs is not a good measure of pool size. It should be noted that our pool size estimate depends on the assumption that under Kyn, mEPSC size is reduced by the same factor (0.5×) as the macroscopic EPSC. Recordings in the presence of Kyn show that mEPSCs are clearly reduced. Unfortunately, an accurate measurement of mEPSC amplitude is not possible, because the smallest mEPSCs are lost in noise. Our pool size estimate would be proportionally smaller if mEPSC amplitude under Kyn were larger than 0.5 times the control value.
Relationship between Ca2+ influx and the release rate per vesicle
If the observed synaptic depression was caused simply by the depletion of a homogeneous RRP, then the release rate per vesicle (ξpv) should remain constant at constant Ca2+ influx or even increase because of facilitation. We calculated ξpv by determining the pool size (see above), calculating the cumulative release as a function of time, and then dividing the release rate (ξ) by the number of remaining synaptic vesicles (see Materials and Methods). For a homogeneous pool, for which the release rate is expected to decay exponentially, this rate per vesicle ξpv is expected to be constant and equal to the rate constant (or the inverse of the time constant) of the release process (Burrone and Lagnado, 2000). We analyzed the traces shown in Figure 3 and calculated ξpv (Fig. 3C). It is seen that for large Ca2+ currents, ξpv decreased with successive pulses, despite the fact that the Ca2+ current amplitude stayed constant. For a homogeneous vesicle pool, we would instead expect an increase in ξpv because of facilitation; however, this was observed only for weak stimuli in which the first pulse elicited little release. In each cell pair, the peak release rates during the first three pulses were plotted against the presynaptic Ca2+ current amplitude (_I_Ca) (Fig.4A), and the relationship was fitted with a Hill function:
| ξpv=ξmaxICanICan+Kn, | Equation 7 |
|---|
or a power function:
when the relationship did not show saturation. The release rate per vesicle during first pulses could be fitted with a third or fourth power function of Ca2+ current (Eq. 8) (n = 3.69 ± 0.36; five cell pairs). Corresponding values for the second and third pulses, however, showed saturation at larger calcium influxes, and the release rates were lower than those observed during the first pulses when the amplitude of Ca2+ current was >1.5 nA. In contrast, ξpv showed facilitation during the second and third pulses when Ca2+ influxes were smaller (<1 nA of Ca2+ current). Similar trends were apparent in data pooled from different cell pairs (Fig.4B). ξpv values during the second and third pulses could be fit empirically with a Hill coefficient (n) of 3−4 (second pulse: n = 3.66 ± 0.11; third pulse n = 3.07 ± 0.44; five cell pairs), and ξmax values during second and third pulses were 0.21 ± 0.02 msec−1 and 0.19 ± 0.03 msec−1, respectively (five cell pairs). Third pulses had slightly smaller exponents. However, because the relationship exceeds the supralinear range, third pulses can also be fitted with the same exponent as the first and second pulses. Specifically, ξpv decreased from an initial value of 0.28 ± 0.05 msec−1during the first pulse to 0.20 ± 0.03 msec−1 and 0.16 ± 0.08 msec−1during second and third pulses, respectively, when the amplitude of the Ca2+ current was relatively large (1460 ± 80 pA). In contrast, facilitation of the rate (0.1–0.2 msec−1) was observed during smaller Ca2+ influxes (when the Ca2+ current was <1 nA) (Fig.4B).
Fig. 4.
Relationship between Ca2+influx and the peak release rate per vesicle. A, The peak release rates per vesicle during the first (+), second (○), and third pulses (●), calculated from the data shown in Figure 3, are plotted against peak Ca2+ current. The data could be fitted with a Hill function (Eq. 7). First pulses were fitted with ξmax = 0.76 msec−1, K = 1320 pA, n = 3.19. Second pulses were fitted with ξmax = 0.35 msec−1, K = 686 pA, n = 3.31. Third pulses were fitted with ξmax = 0.34 msec−1, K = 704 pA, n = 2.36. B, Summary of the relationship between the peak release rate per vesicle during the first (continuous line), second (broken line), and third (dotted line) pulses and the amplitude of Ca2+ current (n = 7 cell pairs). Presynaptic patch pipettes contained 0.05 mm BAPTA.C, Summary of the relationships between the peak release rate per vesicle and the amplitude of Ca2+ current during the first (continuous line), second (broken line), and third (dotted line) pulses. The presynaptic patch pipette contained 0.05 mmEGTA.
We also examined the relationship between ξpvand the Ca2+ influx in the presence of 0.05 mm EGTA (Fig. 4C) (four cell pairs). Qualitatively, results similar to those obtained in the presence of 0.05 mm BAPTA were observed. The relationship between the peak release rate during the first pulses and Ca2+ current was fitted with a power relationship of n = 2.81 ± 0.62, which seemed to be slightly lower in the presence of 0.05 mm EGTA in comparison to 0.05 mm BAPTA. Peak ξpv during the second and third pulses could be fitted with Hill coefficients of 2.94 ± 0.18 and 2.28 ± 0.49 and maximal rates of 0.17 ± 0.02 and 0.21 ± 0.03 (msec−1), respectively. Slight differences in cooperativity (n) between 0.05 mm BAPTA and 0.05 mm EGTA are most likely because of the increased ability of BAPTA to be saturated by short Ca2+ influxes because of its faster Ca2+ binding kinetics. Faster binding increases the apparent cooperativity, as has been demonstrated in a recent modeling study (Bertram et al., 1999).
These results indicate that the release probabilities of synaptic vesicles are heterogeneous; decreases in peak release rates per vesicle during second and third pulses cannot be explained by changes in the Ca2+ stimulus, because peak [Ca2+] values during second and third pulses are probably larger than those during first pulses, because of residual Ca2+ and, possibly, saturation of Ca2+ buffers. Rather, the observed differences are probably a consequence of preferred depletion of a subset of synaptic vesicles that has a high probability of release.
Separating fast- and slow-releasing synaptic vesicle pools by Ca2+ chelators
The dependence of secretion rates on Ca2+ influx is complicated (Fig. 4), because facilitation and preferred depletion of a subset of synaptic vesicles with high release probability occur simultaneously. Because it has been demonstrated in other synapses that exogenous Ca2+ chelators block facilitation by reducing residual Ca2+ (Kamiya and Zucker, 1994; Atluri and Regehr, 1996), it is expected that heterogeneous release processes may be observed more clearly in the presence of an exogenous Ca2+ chelator. Therefore, we examined vesicular release rates in the presence of exogenous Ca2+ chelators introduced via the patch pipette. Specifically, we compared the effects of the slow Ca2+ chelator EGTA with those of the fast Ca2+ chelator BAPTA (Adler et al., 1991). Concentrations of 0.5 mm EGTA and 0.2 mm BAPTA were used, because the introduction of higher concentrations made it impossible to fully deplete the RRP, such that ξpv could not be calculated (data not shown). We will refer to experiments using 0.5 mm EGTA or 0.2 mm BAPTA as performed in high buffering conditions.
In contrast to the case of low Ca2+buffering (control conditions in the presence of 0.05 mmEGTA and 0.05 mm BAPTA), facilitation of both the EPSC and the release rate was largely blocked during low Ca2+ influxes (<1 nA of the Ca2+ current) in the presence of 0.5 mm EGTA (Fig.5A,B). At larger Ca2+ influxes, ξpv decreased with successive pulses (Fig.5A,B). In all protocols, the release rate dropped to values on the order of 10 msec−1 at the end of the depleting pulse. This suggests that the RRP was completely depleted (Fig. 5A). ξpvvalues are plotted against the amplitude of the Ca2+ current in Figure 5B. On average, ξpv of the first pulse is very similar to that obtained in low buffering conditions (Fig. 5C), and the power relation was fit with n = 2.84 ± 0.31. However, facilitation during the second and third pulses was almost entirely blocked in the presence of elevated EGTA (Fig.5B,C). For four cell pairs studied, the relationship between ξpv and Ca2+ current during second and third pulses (Fig. 5B,C) could be fitted empirically with a Hill coefficient (n) of 2.74 ± 0.35 and 2.30 ± 0.08 and ξmax of 0.17 ± 0.03 and 0.135 ± 0.01 msec−1, respectively. At larger Ca2+ influxes, ξpv during second and third pulses approached saturation and was lower than that of first pulses. Averaging among four cell pairs (Fig. 5C), ξpvvalues at a mean Ca2+ current amplitude of 1522 ± 60 pA were 0.26 ± 0.06 msec−1(first pulse), 0.11 ± 0.003 msec−1(second pulse), and 0.08 ± 0.01 msec−1(third pulse). As has been described before, ξpv values during second and third pulses were twice as large (second pulse: 0.2 msec−1; third pulse: 0.16 msec−1) in low buffering conditions (0.05 mm BAPTA), when the mean amplitude of Ca2+ current was comparable (1460 pA). Thus, 0.5 mm EGTA appears to slow down the release of all vesicles by reducing residual Ca2+ and blocking facilitation, regardless of whether vesicles have lower or higher release probabilities.
Because BAPTA binds to Ca2+ (4.5 × 108m−1/sec−1) much faster than EGTA (2.7 × 106m−1sec−1) (Adler et al., 1991; Naraghi, 1997), BAPTA should more strongly affect transmitter release. The same stimulus protocols as shown in Figures 3and 5 were used to examine the relationship between ξpv and Ca2+influx in the presence of 0.2 mm BAPTA (Fig.6) (three cell pairs). With this higher concentration of BAPTA, ξpvs during the first pulse were reduced to <0.05 msec−1 when the amplitude of Ca2+ current was ∼1 nA. In contrast, ξpv values of >0.1 msec−1 were obtained both during low buffering conditions (Fig. 4) and under high EGTA concentrations (Fig. 5C). Thus, 0.2 mm BAPTA was effective in blocking exocytosis of the subset of synaptic vesicles with higher release probabilities. This inhibition seems to be partially overcome by larger Ca2+ influxes, when current amplitude was >1 nA (Fig. 6). Interestingly, facilitation of ξpv was still observed during second and third pulses when Ca2+ influx was small (Fig.6). Such findings can be interpreted as “pseudofacilitation,” which occurs because of saturation of the exogenous fast Ca2+ chelator (Neher, 1998b; Bertram et al., 1999). This phenomenon has already been studied in detail at cortical synapses (Rozov et al., 2001).
Fig. 6.
The effect of 0.2 mm BAPTA on release rates per vesicle. The same stimulus protocols as described in Figure 3were used, and the peak values of release rate per vesicle during the first (continuous line), second (broken line), and third (dotted line) pulses were plotted against the amplitude of the Ca2+ current (n = 3 cell pairs).
Although the protocols described so far readily display facilitation and the reduction of ξpv during second and third pulses, a quantitative interpretation of Figures 4 and 5,B and C, is somewhat complicated by the fact that each value of a given curve represents the situation after some prerelease, which is different between different data points. In the following experiments, we used different protocols to better characterize the individual vesicle subsets.
Heterogeneity of transmitter release observed during long depolarization
Because the presence of EGTA effectively prevents the buildup of residual Ca2+ during long-lasting stimuli (Wu and Borst, 1999), we expected that the use of 0.5 mmEGTA would allow us to resolve distinct components of transmitter release using long depolarizations of the presynaptic terminal. Specifically, the terminal was depolarized from −80 to 70 mV for 4 msec, and then the voltage was shifted back to −10 mV for 50 msec to allow maximum Ca2+ influx (Fig.7A). During this protocol, the amplitude of the Ca2+ current was 1634 ± 126 pA (n = 4 cell pairs) and did not show strong inactivation (Forsythe et al., 1998; Borst and Sakmann, 1999b). More precisely, the Ca2+ current at the end of the 50 msec pulse was 84.0 ± 2.8% of the Ca2+ current during the first 5 msec. Release rates were calculated from deconvolution of the evoked EPSC (Fig. 7B). They increased rapidly after activation of the Ca2+ current and displayed a biexponential decay (Fig. 7). After the decay phase, a small amount of release (<10 msec−1) persisted. Again, this release probably reflects the release of both the remaining releasable vesicles and the newly recruited vesicles. Therefore, we applied a correction to take into account this refilling of vesicles to the RRP. Then, the cumulative release was calculated by integrating the corrected release rate according to Equation 5, and the fraction of released vesicles was plotted against time (Fig.7C). The cumulative plot shows two phases of release that could be fitted with a double exponential. From four cell pairs, the faster time constant was 2.40 ± 0.55 msec, and the slower one was 20.91 ± 4.7 msec. The fast component contributed 53.0 ± 4.3% to the total fit. However, it is possible that the proportion of the faster component may be even larger, because the exponential fit assumes that the slow component begins instantaneously after the depolarization. Also, our estimates for the low release rates after the initial decay cannot be considered very accurate in the presence of a large residual current (Neher and Sakaba, 2001). Even so, the analysis shows that there is a strong deviation from a monoexponential time course of transmitter release at this synapse and suggests that there are at least two classes of vesicles with differing release probabilities (high and low). Interestingly, the time constants indicate that one class of vesicles is five to ten times more likely to release than the other. In this respect, the two components may be somewhat similar to those observed in hippocampal neurons, which were identified using the postsynaptic channel blocker MK-801 (Hessler et al., 1993; Rosenmund et al., 1993). It is also important to mention that although our data were adequately fitted with a double exponential, we cannot exclude the presence of more components. Indeed, the distribution of release probabilities might be continuous, as has been suggested for other synapses (Dobrunz and Stevens, 1997; Huang and Stevens, 1997; Isaacson and Hille, 1997; Murthy et al., 1997; Silver et al., 1998).
Fig. 7.
Time course of quantal release during a long-lasting depolarization in the presence of 0.5 mm EGTA in the presynaptic patch pipette. A, The presynaptic terminal was depolarized from −80 to +70 mV for 4 msec and repolarized to −10 mV for 50 msec (V Pre,top) to elicit a Ca2+ current (IPre, middle). The evoked EPSC (bottom) is shown. The dotted line in the bottom panel indicates the estimated residual current component. B, Release rate estimated from the evoked EPSC is plotted against time. Starting at the time point of 0, the presynaptic terminal was held at −10 mV.C, The cumulative fraction of released vesicles plotted against time. The release rate was integrated after correcting for the effect of refilling of synaptic vesicles to the RRP and was normalized to the total pool size. The data could be fitted with a double exponential, with time constants of 2.01 msec (45%) and 16.64 msec (dotted line).
We also performed a similar set of experiments (long depolarization) in low buffering conditions (0.05 mm BAPTA) (Fig.8). In such experiments, the cumulative amount of release plotted against time could not be readily separated into the two components. In the five cell pairs that we studied, the faster time constant was 3.17 ± 0.85 msec, and the slower one was 6.55 ± 3.55 msec (Fig. 8C). The faster component contributed significantly more (76.0 ± 12.5%) to the total fit than in high buffering conditions, whereas its time constant was slightly slower. This may well be a consequence of the difficulty in separating components, combined with restricted time resolution of the deconvolution procedure. The time constant of the slow component, at a given Ca2+ current amplitude, was faster. Contrary to release rates, the amplitudes of the presynaptic Ca2+ currents (1895 ± 154 pA) were not substantially different from those of cell pairs in the presence of 0.5 mm EGTA. Similar results were also observed in the presence of 0.05 mm EGTA (five cell pairs; data not shown). These results suggest that the accumulation of presynaptic Ca2+ accelerates the release of the slow component. Therefore, the two components of release are not as clearly separated as in the case of 0.5 mmEGTA, which lowers residual Ca2+.
Fig. 8.
Time course of quantal release during long pulses in the presence of 0.05 mm BAPTA in the patch pipette.A, The presynaptic terminal was depolarized from −80 to +70 mV for 4 msec and was held at −10 mV for 20 msec (V Pre) to elicit presynaptic Ca2+ current (IPre). The dotted line shows an estimate of the residual current component.B, Release rate plotted against time. Starting at the time point of 0, the presynaptic terminal was held at −10 mV.C, The cumulative fraction of vesicles released is plotted against time. The data could be fitted with double exponentials with time constants of 1.09 msec (68%) and 5.92 msec (dotted line).
Ca2+ dependence of the slow component
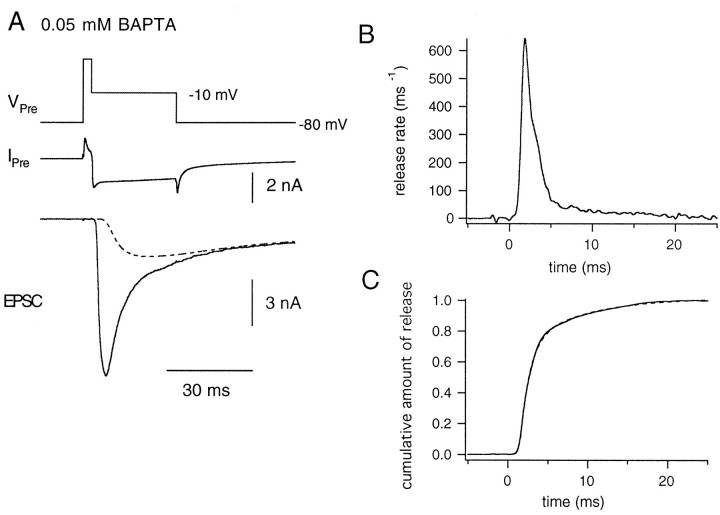
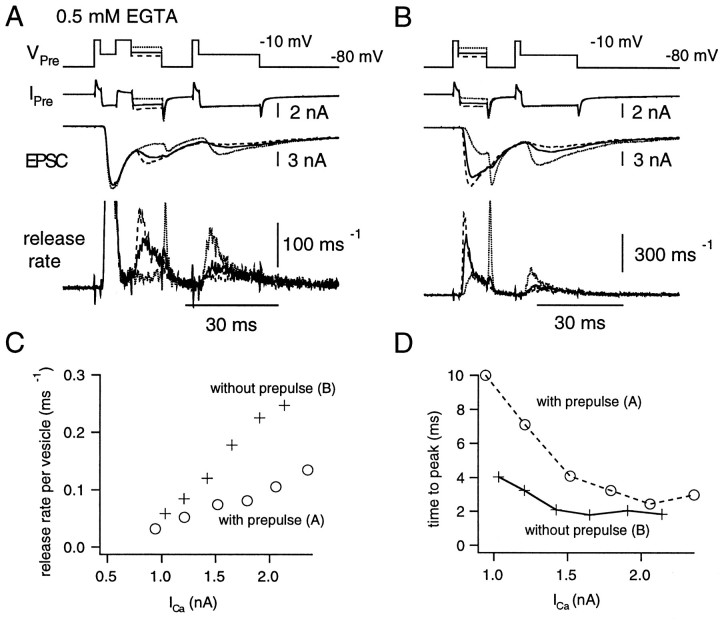
To examine the Ca2+ dependence of the slow component, we applied depolarizing pulses (test pulse, 10 msec in duration) of various amplitudes after depleting most of the faster component by prepulses of a fixed amplitude (depolarization to −10 mV for 4–6 msec; constant duration within each cell pair). The duration of the prepulse was adjusted to deplete most of the faster component, considering that the time constant of the faster component is 2–3 msec (Fig. 7C). At the end of the protocol, the presynaptic terminal was held at −10 mV for 20 msec to completely deplete the RRP (Fig. 9A). Subsequently, a similar sequence of pulses was applied without prepulses to examine the dependence of the fast component on Ca2+influx (Fig. 9B) in the same cell pair.
Fig. 9.
Prepulse experiment for studying the Ca2+ dependence of the slower component.A, Depolarizing pulses (test pulse; 10 msec in duration) of various amplitudes (from −20 to +30 mV) were applied after a fixed prepulse (depolarization to −10 mV for 5 msec). In all protocols, the terminal was finally depolarized to −10 mV for 20 msec, to deplete the RRP. From top, V Pre,IPre, EPSC, and_release rate_ are shown. B, The same protocol as described in A except that the prepulse was omitted. The same cell pair as in A was used.C, The peak release rate per vesicle during the test pulse in the presence (○) or absence (+) of the prepulse, is plotted against the amplitude of Ca2+ current. The data are from the same cell pair as in A and B. D, The time-to-peak of the release rate per vesicle during the test pulse in the presence (○) or absence (+) of the prepulse is plotted against the amplitude of Ca2+current. The data are from the same cell pair as A and_B_. Note that the time-to-peak cannot exceed 10 msec, because the pulse duration is 10 msec.
Experiments were performed with high concentrations of EGTA (0.5 mm) to allow a clear separation of the fast and the slow components (Figs. 9,10A,B). The peak release rate per vesicle (ξpv) during the test pulse was plotted against the amplitude of the Ca2+ current (Fig. 9C; pooled data in Fig. 10A). The dependence of the release rate on the Ca2+ current was less steep when prepulses were present than when prepulses were absent. At 2 nA of Ca2+ current, ξpvduring the test pulse in the presence of a prepulse was ∼0.1 msec−1, whereas it was >0.2 msec−1 in the absence of the prepulse (Fig. 10A). The time-to-peak of ξpv was also measured for each test pulse and plotted against the amplitude of Ca2+ current (Figs. 9D,10B). The time-to-peak was significantly longer when prepulses were applied. By increasing the Ca2+ influx, differences between the time-to-peak between test pulses with and without prepulses became smaller. These findings seem to suggest that some buildup of Ca2+ is necessary to activate release of the slower component.
Fig. 10.
Prepulse experiment in the presence of 0.5 mm EGTA. A, B, The peak release rate per vesicle (A) and the time-to-peak of the release rate per vesicle (B) during the test pulses (Fig. 9) are plotted against the amplitude of Ca2+ current. Presynaptic patch pipettes contained 0.5 mm EGTA. The data are averages from five cell pairs. Note that the time-to-peak cannot exceed 10 msec, because the pulse duration is 10 msec (the same for D). C,D, The peak release rate per vesicle (C) and the time-to-peak of the release rate per vesicle (D) during test pulses are plotted against the amplitude of Ca2+ current. Presynaptic patch pipettes contained 0.05 mm BAPTA. The data are averages from six cell pairs.
For comparison, the same experiments were performed in low buffering conditions (0.05 mm BAPTA) (Fig.10C,D). Then, a more complex behavior was observed. The ξpv during the test pulse was facilitated by the prepulse when the amplitude of Ca2+ current was <800 pA. In contrast, the peak ξpv during the test pulse was depressed by the prepulse when the amplitude of Ca2+ current became >1 nA. In the presence of the prepulse and for Ca2+currents between 1.5 and 2.0 nA, the peak ξpvduring the test pulse was larger (0.2 msec−1) in the low buffering condition (Fig. 10C) than in high buffering conditions (0.1 msec−1) (Fig. 10A). These results suggest that accumulation of presynaptic Ca2+ facilitates the release of the slow component and that this facilitation is prevented by higher concentrations of EGTA. The relationship between the time-to-peak of ξpv and the amplitude of the Ca2+ current also supports this idea (Fig.10D). The time-to-peak during the test pulse in the presence of the prepulse was the same or even shorter than in the absence of the prepulse. Again, this is in contrast to findings under high buffering conditions (Fig. 10B) and suggests that accumulation of presynaptic Ca2+ facilitates the release of the slow component.
Recruitment of the slow component by elevating extracellular Ca2+
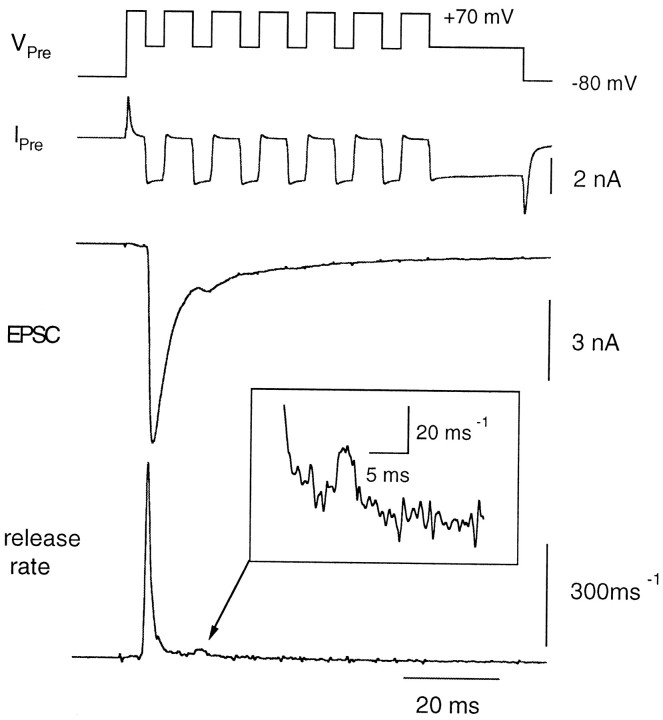
The accumulation of presynaptic Ca2+accelerates the release of the slow component. Then, sufficient concentrations of presynaptic Ca2+ should be able to activate release of the slow component with rates comparable to those of the fast component in normal conditions. We tested this expectation by elevating the extracellular Ca2+ concentration to 10 mmand examining the release rates under low buffering conditions (0.05 mm BAPTA). The presynaptic terminal was depolarized from −80 to +70 mV and repolarized every 10 msec to −10 mV for 4 msec to allow Ca2+ influx into the terminal (Fig.11). The average amplitude of the Ca2+ current was 2650 ± 167 pA during the first pulse (n = 6 cell pairs). Inactivation of the Ca2+ current (Forsythe et al., 1998; Borst and Sakmann 1999b) was not prominent with the pulse protocol used (Fig. 11). The evoked EPSC was depressed strongly during the second pulse, and the release rate was constant and low during further stimuli. The ratio of cumulative release evoked by the second pulse to the first pulse was 0.14 ± 0.02 (n = 6 cell pairs). The time-to-peak of the release rate during the first pulse was 1.21 ± 0.39 msec, and the rate began to decay during the pulse (Fig. 11). The decay could be fitted by a single exponential with a time constant of 1.71 ± 0.72 msec. The peak release rate per vesicle during the first pulse was 0.51 ± 0.06 msec−1, indicating that most of readily releasable synaptic vesicles could be depleted within the first 4 msec of depolarization. The result is consistent with the idea that the slow component can be released quite rapidly once presynaptic Ca2+concentrations reach a certain level. Therefore, the slow component will most likely contribute to nerve-evoked release when Ca2+ concentration builds up during trains of action potentials.
Fig. 11.
Release rates observed in the presence of 10 mm extracellular Ca2+. Extracellular Ca2+ was increased to 10 mm to augment the amplitudes of the Ca2+ currents. The presynaptic terminal was depolarized from −80 to +70 mV and repolarized every 10 msec to −10 mV for 4 msec. After repeating this stimulus six times, the terminal was held at −5 mV for 20 msec to deplete the RRP (_V_Pre). Release rates (bottom) were calculated from the evoked EPSC.
DISCUSSION
The calyx of Held offers unique possibilities for the study of synaptic transmission by allowing an analysis of the relationship between Ca2+ influx and rates of secretion under voltage clamp in both presynaptic and postsynaptic compartments (Borst et al., 1995; Takahashi et al., 1996). A new variant of deconvolution, which we developed (Neher and Sakaba, 2001), allows a direct calculation of rates of release in the presence of CTZ and Kyn, under which quantal size was shown to be constant over a wide range of stimulation protocols examined (Neher and Sakaba, 2001). Because Kyn is displaced by glutamate in its sustained presence (Diamond and Jahr, 1997), one may argue that under Kyn, quantal size changes in an activity-dependent manner, especially at high release rates. This possibility was not examined directly in the companion paper (Neher and Sakaba, 2001). It would compromise some of our results, because we assume constant mEPSC size throughout. However, we think this is very unlikely, because we did not observe any increase in quantal sizes immediately after strong stimulation [“late noise” protocol inNeher and Sakaba (2001)], and because Kyn depressed EPSCs without changing their time course significantly, when we used presynaptic stimulation protocols similar to those used here (data not shown). Such changes should occur if displacement takes place.
Using the deconvolution method, we show that the peak rate of release varies according to a power function of the amplitude of Ca2+ current with an exponent of 3–4, when a first short pulse of Ca2+ influx is applied after a pause of at least 10 sec (Borst and Sakmann, 1996,1999a; Schneggenburger et al., 1999; Wu et al., 1999). We also show that the Ca2+ influx becomes more efficient in eliciting release when it is preceded by low-level Ca2+ influx (Figs. 3, 4). This effect is dominating as long as only moderate release has occurred (Figs. 3, 4). The enhancement is blocked by 0.5 mm EGTA (Figs. 5, 10), a finding that is also characteristic of synaptic facilitation (Atluri and Regehr, 1996). We therefore propose that this effect of preceding Ca2+ influx is the voltage clamp equivalent to paired-pulse facilitation. We further show that the opposite tendency is observed, once a sizable fraction of the readily releasable vesicles has been released: the remaining vesicles are released at lower rate constants and with more delay at a given Ca2+ current (Figs. 3-5, 7-10). However, larger Ca2+ influx, which can be obtained for instance with higher extracellular Ca2+ concentration, restores release at high rates (Figs. 10C,D, 11; also compare Figs. 7and 8). The two effects overlap, leading to a complicated dependence of secretion rates on Ca2+ influx within trains of stimuli.
Increased availability of Ca2+, either as residual Ca2+ or bound to sites, was suggested as a mechanism of facilitation (for review, see Zucker 1999). Our data allow some inferences to be made regarding this issue. In Figure 4B, a given Ca2+current evokes release rates that are higher during second and third pulses than those during a first pulse (for Ca2+ currents <1 nA) (Fig.4B). Therefore, facilitation increases the effectiveness of Ca2+ influx for eliciting secretion. Previous models and data on facilitation suggested that Ca2+ bound to a special high-affinity facilitation site would mediate this effect (Kamiya and Zucker, 1994;Atluri and Regehr, 1996). Alternatively, several sites with graded affinities were assumed (Stanley, 1986; Wright et al., 1996). In the latter model, the exponent of the power law describing a facilitated synaptic transfer function is expected to be different from that of the nonfacilitated one. At the calyx of Held, however, the relationships between the peak rate constant (ξpv) and the Ca2+ influx had similar exponents, when comparing first and second pulses (Fig. 4A).
An alternative explanation for facilitation is the augmentation of the effectiveness of Ca2+ influx in raising Ca2+ concentration ([Ca2+]) at release sites (Katz and Miledi, 1968; Neher, 1998b). From the relationship between the peak ξpv and the Ca2+influx during first pulses and by assuming that the [Ca2+] increment during a stimulus is proportional to the Ca2+ influx, we estimate that [Ca2+] should be higher by 20–40% during second and third pulses, compared with first pulses. According to a straightforward residual Ca2+ hypothesis (Ravin et al., 1997,1999), this increase should be caused totally by residual Ca2+ remaining after the conditioning pulse, superimposing linearly onto the [Ca2+] increment elicited by the test pulse. However, considering the low concentration of residual Ca2+ measured after action potential stimulation (<1 μm) (Helmchen et al., 1997), the [Ca2+] increment at the release site responsible for triggering transmitter release must be low (<5 μm) if this type of residual Ca2+ hypothesis is correct. Experimental evidence, on the other hand, points to [Ca2+] increments in the range of 10–25 μm at active zones during action potentials (Bollmann et al., 2000; Schneggenburger and Neher, 2000). It is necessary, therefore, to assume nonlinear mechanisms regarding the superposition of residual Ca2+ and the [Ca2+] increment, such as buffer saturation (Neher, 1998b; Bennett et al., 2000), to reconcile these two pieces of evidence with the postulate that facilitation is caused entirely by an increase in Ca2+concentration at the release site.
Synaptic depression shows up in our data as a rapid decrease in secretion rate at constant Ca2+ influx (Figs. 3, 4). We interpret this as a consumption of release-ready vesicles with high intrinsic Ca2+sensitivity. Once ∼50% of the RRP have been consumed, the remaining vesicles seem to have quite small release rates (at a given Ca2+ influx) (Figs. 7, 9). A similar decrease in the rate constant of exocytosis at constant_I_Ca was described recently at the giant terminals of retinal bipolar cells (Burrone and Lagnado, 2000). We would like to discuss five possible mechanisms for the heterogeneity of synaptic vesicle properties: (1) positional heterogeneity, (2) molecular heterogeneity, (3) inhibitory effect of prerelease, (4) adaptation of the release apparatus, and (5) remaining postsynaptic effects.
The first two mechanisms assume that there is a pre-existing heterogeneity among vesicles that may be attributable to heterogeneous spatial arrangements between Ca2+ channels and release sites. There is good reason to assume positional heterogeneity, because it is known that Ca2+ channels interact with syntaxin (Sheng et al., 1994, 1996; Rettig et al., 1996), that this interaction has functional consequences (Mochida et al., 1996; Rettig et al., 1997), and that there are accumulations of Ca2+ channels at active zones (Haydon et al., 1994). The degree to which Ca2+channels couple or accumulate may show statistical variations among release sites because only a small number of channels are likely to be involved. Thus, a vesicle docked to a release site that happens to have more Ca2+ channels in its immediate surrounding will be released much more readily than the average vesicle during a first stimulus (Quastel et al., 1992; Neher, 1998b; Bennett et al., 2000). The remaining vesicles are likely to have fewer Ca2+ channels in their neighborhood (or channels at larger distance) and, on average, will require higher Ca2+ currents during subsequent stimuli to be released as rapidly as those during the first stimulus. Our data, at first sight, readily conform with the expectations from such a mechanism. ξpv, the release rate per remaining vesicle, is smaller for second and third pulses, and notably, the time-to-peak of ξpv increases (Fig.10B). Both effects would be expected if average distances between release sites and Ca2+channels were increased. However, longer times to peak together with smaller peak rates would also be expected if the Ca2+ signal were reduced at constant geometry. Thus, it is more appropriate to compare the time-to-peak of those responses that have similar peak secretion rates (compare values in Fig. 10, A and B). One can see that for any such pairs the time-to-peak values are indeed quite similar, except when the Ca2+ current was very small (500 pA). Therefore, our data cannot be taken as strong evidence for a simple geometric cause for the observed heterogeneity.
The situation is different for the case of low buffering (Fig.10D), where times to peak are longer for first pulses throughout the whole current range. However, this may be caused by a slow global buildup of Ca2+ (in the absence of strong buffers), which may lead to a prolonged rise in release rate or increasing facilitation of transmitter release.
Second, the heterogeneity may also be caused by differences in the molecular state of the release machinery. In neurosecretory cells it was found by flash photolysis of caged Ca2+ that secretion proceeds with two kinetic components (at fixed Ca2+concentration). This was interpreted to represent two different states of soluble _N_-ethylmaleimide-sensitive factor attachment protein receptor complexes (Xu et al., 1999). It may well be that also in synaptic vesicles the fusion machinery can exist in different molecular states, either because of heterogeneity of its components or because of modulatory processes. If so, our data would be most readily explained if the reduced ξpv of reluctant vesicles were caused by a reduced binding rate of Ca2+ to a Ca2+ sensor. The alternative explanations (increased dissociation rate of Ca2+ or reduced maximum fusion rate) are ruled out by the slower kinetics of secretion and by the fact that ξpv can be increased to high values by increasing Ca2+ influx.
The remaining mechanisms [(3) to (5) in the above text] assume that heterogeneity does not exist a priori but is an immediate consequence of the preceding release. So-called “lateral inhibition” (i.e., inhibition of release of a second and third vesicle at a given active zone as a consequence of a first release) has been postulated for synapses of hippocampal neurons (Dobrunz et al., 1997). However, this was reported to have a characteristic duration on the order of 10 msec. No sign of decay of such lateral inhibition on this time scale could be observed in our experiments. Alternatively, the secretory apparatus might adapt to elevated Ca2+ concentration (Stuenkel and Nordmann, 1993; Hsu et al., 1996). In that case, one has to assume, however, that adaptation can be overcome by sufficiently high Ca2+ concentration. Postsynaptic receptor desensitization as a consequence of preceding release would lead to an apparent decrease in ξpv, because our deconvolution analysis assumes constant quantum size. However, our experiments combining noise analysis with deconvolution (Neher and Sakaba, 2001) showed that under the conditions used here (presence of cyclothiazide and kynurenic acid), the quantum size is constant for a wide variety of stimulation conditions. It does decrease, however, if no drugs are added to the extracellular solution.
In summary, some features of our data can be interpreted by positional heterogeneity. However, we cannot exclude the possibility that molecular heterogeneity plays a role. The latter mechanism might provide multiple options for modulation of the secretory process by kinases and other regulatory proteins.
For a simple mechanism of synaptic depression, in which a constant fraction of a homogeneous pool of vesicles is consumed during each action potential, one would expect a geometric decay of the EPSC within a train of action potentials. Steady-state release would follow a simple 1/f law at high frequencies (f). In many synapses, including the calyx of Held, the steady-state depression is shallower than 1/f, and responses persist on a plateau higher than that expected from the initial decay (Liley and North, 1953; Weis et al., 1999). Our data give a clue to such a behavior in agreement with a recent analysis (Wu and Borst, 1999). In physiological conditions, slowly releasing vesicles are expected not to participate appreciably during the first few pulses in a train of stimuli. However, once the rapidly releasing vesicles are consumed, slowly releasing vesicles are the only ones remaining. Wu and Borst (1999) recently showed that slowly releasing vesicles are very rapidly recruited to the RRP. Our data now show that in the absence of Ca2+ buffer, repetitive stimulation leads to an increase in their release rate (Figs. 3, 4, 8, 10). Thus, we suggest that during continuous high-frequency stimulation, rapidly replenished vesicles may very well contribute to maintained synaptic transmission (Borst et al., 1995; von Gersdorff et al., 1997), although they are of the slow-releasing variety. Thus, rapid recruitment, as an intrinsic property of a subset of vesicles in the RRP, may be a mechanism for maintained activity of depressing synapses at high stimulation frequencies. This mechanism may act in addition or alternatively to Ca2+-mediated augmentation of vesicle recruitment (Dittman and Regehr, 1998; Stevens and Wesseling, 1998; Wang and Kaczmarek, 1998) to counteract deep depression. On the other hand, during a high-frequency train of action potentials, desensitization of postsynaptic receptors (Trussell et al., 1993; Otis et al., 1996; Neher and Sakaba, 2001), inactivation of presynaptic Ca2+ currents (Forsythe et al., 1998), depletion of Ca2+ in the synaptic cleft (Borst and Sakmann, 1999b), and the activation of metabotropic glutamate receptors (Takahashi et al., 1996; but see von Gersdorff et al., 1997) may intensify synaptic depresion. The calyx of Held offers the possibility of studying these mechanisms separately.
Footnotes
This work was supported in part by a grant of the Deutsche Forschungsgemeinschaft (SFB 406) to E.N. and by an Alexander von Humboldt fellowship (T.S.). We thank Ralf Schneggenburger for very helpful advice during the course of this study and Alexander Meyer, Ralf Schneggenburger, and Henrique von Gersdorff for help with the initial part of the experiments. We also thank Isabel Llano, Alain Marty, and Sonja Pyott for critical comments on this manuscript.
Correspondence should be addressed to Erwin Neher, Max-Planck-Institute for Biophysical Chemistry, Department of Membrane Biophysics, D-37077, Göttingen, Germany. E-mail:eneher@gwdg.de.
REFERENCES
- 1.Adler EM, Augustine GJ, Duffy SN, Charlton MP. Alien intracellular calcium chelators attenuate neurotransmitter release at the squid giant synapse. J Neurosci. 1991;11:1496–1507. doi: 10.1523/JNEUROSCI.11-06-01496.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Atluri PP, Regehr WG. Determinants of the time course of facilitation at the granule cell to Purkinje cell synapse. J Neurosci. 1996;16:5661–5671. doi: 10.1523/JNEUROSCI.16-18-05661.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Auger C, Kondo S, Marty A. Multivesicular release at single functional synaptic sites in cerebellar stellate and basket cells. J Neurosci. 1998;18:4532–4547. doi: 10.1523/JNEUROSCI.18-12-04532.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barbour B, Keller BU, Llano I, Marty A. Prolonged presence of glutamate during excitatory synaptic transmission to cerebellar Purkinje cells. Neuron. 1994;12:1331–1343. doi: 10.1016/0896-6273(94)90448-0. [DOI] [PubMed] [Google Scholar]
- 5.Barnes-Davies M, Forsythe ID. Pre- and postsynaptic glutamate receptors at a giant excitatory synapse in rat auditory brainstem slices. J Physiol (Lond) 1995;488:387–406. doi: 10.1113/jphysiol.1995.sp020974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bellingham MC, Walmsley B. A novel presynaptic inhibitory mechanism underlies paired pulse depression at a fast central synapse. Neuron. 1999;23:159–170. doi: 10.1016/s0896-6273(00)80762-x. [DOI] [PubMed] [Google Scholar]
- 7.Bennett MR, Farnell L, Gibson WG. The probability of quantal secretion within an array of calcium channels of an active zone. Biophys J. 2000;78:2222–2240. doi: 10.1016/S0006-3495(00)76770-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bertram R, Smith GD, Sherman A. Modeling study of the effects of overlapping Ca2+ microdomains on neurotransmitter release. Biophys J. 1999;76:735–750. doi: 10.1016/S0006-3495(99)77240-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bollmann JH, Sakmann B, Borst JGG. Calcium sensitivity of glutamate release in a calyx-type terminal. Science. 2000;289:953–957. doi: 10.1126/science.289.5481.953. [DOI] [PubMed] [Google Scholar]
- 10.Borges S, Gleason E, Turelli M, Wilson M. The kinetics of quantal transmitter release from retinal amacrine cells. Proc Natl Acad Sci USA. 1995;92:6896–6900. doi: 10.1073/pnas.92.15.6896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Borst JG, Sakmann B. Calcium influx and transmitter release in a fast CNS synapse. Nature. 1996;383:431–434. doi: 10.1038/383431a0. [DOI] [PubMed] [Google Scholar]
- 12.Borst JG, Sakmann B. Facilitation of presynaptic calcium currents in the rat brainstem. J Physiol (Lond) 1998;513:149–155. doi: 10.1111/j.1469-7793.1998.149by.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Borst JG, Sakmann B. Effect of changes in action potential shape on calcium currents and transmitter release in a calyx-type synapse of the rat auditory brainstem. Philos Trans R Soc Lond B Biol Sci. 1999a;354:347–355. doi: 10.1098/rstb.1999.0386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Borst JGG, Sakmann B. Depletion of calcium in the synaptic cleft of a calyx-type synapse in the rat brainstem. J Physiol (Lond) 1999b;521:123–133. doi: 10.1111/j.1469-7793.1999.00123.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Borst JG, Helmchen F, Sakmann B. Pre- and postsynaptic whole-cell recordings in the medial nucleus of the trapezoid body of the rat. J Physiol (Lond) 1995;489:825–840. doi: 10.1113/jphysiol.1995.sp021095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Burrone J, Lagnado L. Synaptic depression and the kinetics of exocytosis in retinal bipolar cells. J Neurosci. 2000;15:568–578. doi: 10.1523/JNEUROSCI.20-02-00568.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cuttle MF, Tsujimoto T, Forsythe ID, Takahashi T. Facilitation of the presynaptic calcium current at an auditory synapse in rat brainstem. J Physiol (Lond) 1998;512:723–729. doi: 10.1111/j.1469-7793.1998.723bd.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Diamond JS, Jahr CE. Asynchronous release of synaptic vesicles determines the time course of the AMPA receptor-mediated EPSC. Neuron. 1995;15:1097–1107. doi: 10.1016/0896-6273(95)90098-5. [DOI] [PubMed] [Google Scholar]
- 19.Diamond JS, Jahr CE. Transporters buffer synaptically released glutamate on a submillisecond scale. J Neurosci. 1997;17:4672–4687. doi: 10.1523/JNEUROSCI.17-12-04672.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dittman JS, Regehr WG. Calcium dependence and recovery kinetics of presynaptic depression at a fast central synapse. J Neurosci. 1998;18:6147–6162. doi: 10.1523/JNEUROSCI.18-16-06147.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dobrunz LE, Stevens CF. Heterogeneity of release probability, facilitation, and depletion at central synapses. Neuron. 1997;18:995–1008. doi: 10.1016/s0896-6273(00)80338-4. [DOI] [PubMed] [Google Scholar]
- 22.Dobrunz LE, Huang EP, Stevens CF. Very short-term plasticity in hippocampal synapses. Proc Natl Acad Sci USA. 1997;94:14843–14847. doi: 10.1073/pnas.94.26.14843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Forsythe ID, Tsujimoto T, Barnes-Davies M, Cuttle MF, Takahashi T. Inactivation of presynaptic calcium current contributes to synaptic depression at a fast central synapse. Neuron. 1998;20:797–807. doi: 10.1016/s0896-6273(00)81017-x. [DOI] [PubMed] [Google Scholar]
- 24.Hartzell HC, Kuffler SW, Yoshikami D. Post-synaptic potentiation: interaction between quanta of acetylcholine at the skeletal neuromuscular synapse. J Physiol (Lond) 1975;251:427–463. doi: 10.1113/jphysiol.1975.sp011102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Haydon PG, Henderson E, Stanley EF. Localization of individual calcium channels at the release face of a presynaptic nerve terminal. Neuron. 1994;13:1275–1280. doi: 10.1016/0896-6273(94)90414-6. [DOI] [PubMed] [Google Scholar]
- 26.Helmchen F, Borst JGG, Sakmann B. Calcium dynamics associated with a single action potential in a CNS presynaptic terminal. Biophys J. 1997;72:1458–1471. doi: 10.1016/S0006-3495(97)78792-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hessler NA, Shirke AM, Malinow R. The probability of transmitter release at a mammalian central synapse. Nature. 1993;366:569–572. doi: 10.1038/366569a0. [DOI] [PubMed] [Google Scholar]
- 28.Hsu SF, Augustine GJ, Jackson MB. Adaptation of Ca2+-triggered exocytosis in presynaptic terminals. Neuron. 1996;17:501–512. doi: 10.1016/s0896-6273(00)80182-8. [DOI] [PubMed] [Google Scholar]
- 29.Huang EP, Stevens CF. Estimating the distribution of synaptic reliabilities. J Neurophysiol. 1997;78:2870–2880. doi: 10.1152/jn.1997.78.6.2870. [DOI] [PubMed] [Google Scholar]
- 30.Isaacson JS, Hille B. GABAB-mediated presynaptic inhibition of excitatory transmission and synaptic vesicle dynamics in cultural hippocampal neurons. Neuron. 1997;18:143–152. doi: 10.1016/s0896-6273(01)80053-2. [DOI] [PubMed] [Google Scholar]
- 31.Isaacson JS, Walmsley B. Amplitude and time course of spontaneous and evoked excitatory postsynaptic currents in bushy cells of the anteroventral cochlear nucleus. J Neurophysiol. 1996;76:1566–1571. doi: 10.1152/jn.1996.76.3.1566. [DOI] [PubMed] [Google Scholar]
- 32.Jonas P, Major G, Sakmann B. Quantal components of unitary EPSCs at the mossy fibre synapse on CA3 pyramidal cells of rat hippocampus. J Physiol (Lond) 1993;472:615–663. doi: 10.1113/jphysiol.1993.sp019965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kamiya H, Zucker RS. Residual Ca2+ and short-term synaptic plasticity. Nature. 1994;371:603–606. doi: 10.1038/371603a0. [DOI] [PubMed] [Google Scholar]
- 34.Katz B, Miledi R. The role of calcium in neuromuscular facilitation. J Physiol (Lond) 1968;195:481–492. doi: 10.1113/jphysiol.1968.sp008469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liley AW, North KAK. An electrical investigation of effects of repetitive stimulation on mammalian neuromuscular junction. J Neurophysiol. 1953;16:509–527. doi: 10.1152/jn.1953.16.5.509. [DOI] [PubMed] [Google Scholar]
- 36.Magleby KL, Pallotta BS. A study of desensitization of acetylcholine receptors using nerve-released transmitter in the frog. J Physiol (Lond) 1981;316:225–250. doi: 10.1113/jphysiol.1981.sp013784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mennerick S, Zorumski CF. Presynaptic influence on the time course of fast excitatory synaptic currents in cultured hippocampal cells. J Neurosci. 1995;15:3178–3192. doi: 10.1523/JNEUROSCI.15-04-03178.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mochida S, Sheng ZH, Baker C, Kobayashi H, Catterall WA. Inhibition of neurotransmission by peptides containing the synaptic protein interaction site of N-type Ca2+ channels. Neuron. 1996;17:781–788. doi: 10.1016/s0896-6273(00)80209-3. [DOI] [PubMed] [Google Scholar]
- 39.Murthy VN, Sejnowski TJ, Stevens CF. Heterogeneous release probabilities of visualized individual hippocampal synapses. Neuron. 1997;18:599–612. doi: 10.1016/s0896-6273(00)80301-3. [DOI] [PubMed] [Google Scholar]
- 40.Naraghi M. T-jump study of calcium binding kinetics of calcium chelators. Cell Calcium. 1997;22:255–268. doi: 10.1016/s0143-4160(97)90064-6. [DOI] [PubMed] [Google Scholar]
- 41.Neher E. Vesicle pools and Ca2+ microdomains: new tools for understanding their roles in neurotransmitter release. Neuron. 1998a;20:389–399. doi: 10.1016/s0896-6273(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 42.Neher E. Usefulness and limitations of linear approximations to the understanding of Ca++ signals. Cell Calcium. 1998b;24:345–357. doi: 10.1016/s0143-4160(98)90058-6. [DOI] [PubMed] [Google Scholar]
- 43.Neher E, Sakaba T. Combining deconvolution and noise analysis for the estimation of transmitter release rates at the calyx of Held. J Neurosci. 2001;21:429–445. doi: 10.1523/JNEUROSCI.21-02-00444.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Otis T, Zhang S, Trussell LO. Direct measurement of AMPA receptor desensitization induced by glutamatergic synaptic transmission. J Neurosci. 1996;16:7496–7504. doi: 10.1523/JNEUROSCI.16-23-07496.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Quastel DM, Guan YY, Saint DA. The relation between transmitter release and Ca2+ entry at the mouse motor nerve terminal: role of stochastic factors causing heterogeneity. Neuroscience. 1992;51:657–671. doi: 10.1016/0306-4522(92)90305-l. [DOI] [PubMed] [Google Scholar]
- 46.Ravin R, Spira ME, Parnas H, Parnas I. Simultaneous measurement of intracellular Ca2+ and asynchronous transmitter release from the same crayfish bouton. J Physiol (Lond) 1997;501:251–262. doi: 10.1111/j.1469-7793.1997.tb00001.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ravin R, Parnas H, Spira ME, Volfovsky N, Parnas I. Simultaneous measurement of evoked release and [Ca2+]I in a crayfish release bouton reveals high affinity of release to Ca2+. J Neurophysiol. 1999;81:634–642. doi: 10.1152/jn.1999.81.2.634. [DOI] [PubMed] [Google Scholar]
- 48.Rettig J, Sheng ZH, Kim DK, Hodson CD, Snutch TP, Catterall WA. Isoform-specific interaction of the alpha1A subunits of brain Ca2+ channels with the presynaptic proteins syntaxin and SNAP-25. Proc Natl Acad Sci USA. 1996;93:7363–7368. doi: 10.1073/pnas.93.14.7363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rettig J, Heinemann C, Ashery U, Sheng ZH, Yokoyama CT, Catterall WA, Neher E. Alteration of Ca2+ dependence of neurotransmitter release by disruption of Ca2+ channel/syntaxin interaction. J Neurosci. 1997;17:6647–6656. doi: 10.1523/JNEUROSCI.17-17-06647.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rosenmund C, Clements JD, Westbrook GL. Nonuniform probability of glutamate release at a hippocampal synapse. Science. 1993;262:754–757. doi: 10.1126/science.7901909. [DOI] [PubMed] [Google Scholar]
- 51.Rozov A, Burnashev N, Sakmann B, Neher E (2001) Transmitter release modulation by intracellular Ca2+buffers in facilitating and depressing nerve terminals of pyramidal cells in layer 2/3 of the rat neocortex indicates a target specific difference in presynaptic calcium dynamics. J Physiol (Lond), in press. [DOI] [PMC free article] [PubMed]
- 52.Schneggenburger R, Neher E. Intracellular calcium dependence of transmitter release rates at a fast central synapse. Nature. 2000;406:889–893. doi: 10.1038/35022702. [DOI] [PubMed] [Google Scholar]
- 53.Schneggenburger R, Meyer AC, Neher E. Released fraction and total size of a pool of immediately available transmitter quanta at a calyx synapse. Neuron. 1999;23:399–409. doi: 10.1016/s0896-6273(00)80789-8. [DOI] [PubMed] [Google Scholar]
- 54.Sheng ZH, Rettig J, Takahashi M, Catterall WA. Identification of a syntaxin-binding site on N-type calcium channels. Neuron. 1994;13:1303–1313. doi: 10.1016/0896-6273(94)90417-0. [DOI] [PubMed] [Google Scholar]
- 55.Sheng ZH, Rettig J, Cook T, Catterall WA. Calcium-dependent interaction of N-type calcium channels with the synaptic core complex. Nature. 1996;379:451–454. doi: 10.1038/379451a0. [DOI] [PubMed] [Google Scholar]
- 56.Silver RA, Cull-Candy SG, Takahashi T. Non-NMDA glutamate receptor occupancy and open probability at a rat cerebellar synapse with single and multiple release sites. J Physiol (Lond) 1996;494:231–250. doi: 10.1113/jphysiol.1996.sp021487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Silver RA, Momiyama A, Cull-Candy SG. Locus of frequency-dependent depression identified with multiple-probability fluctuation analysis at rat climbing fibre-Purkinje cell synapses. J Physiol (Lond) 1998;510:881–902. doi: 10.1111/j.1469-7793.1998.881bj.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Stanley EF. Decline in calcium cooperativity as the basis of facilitation at the squid giant synapse. J Neurosci. 1986;6:782–789. doi: 10.1523/JNEUROSCI.06-03-00782.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Stevens CF, Wesseling JF. Activity-dependent modulation of the rate at which synaptic vesicles become available to undergo exocytosis. Neuron. 1998;21:415–424. doi: 10.1016/s0896-6273(00)80550-4. [DOI] [PubMed] [Google Scholar]
- 60.Stuenkel EL, Nordmann JJ. Intracellular calcium and vasopression release of rat isolated neurohypophysical nerve endings. J Physiol (Lond) 1993;468:335–355. doi: 10.1113/jphysiol.1993.sp019775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Takahashi T, Forsythe ID, Tsujimoto T, Barnes-Davies M, Onodera K. Presynaptic calcium current modulation by a metabotropic glutamate receptor. Science. 1996;274:594–597. doi: 10.1126/science.274.5287.594. [DOI] [PubMed] [Google Scholar]
- 62.Tang CM, Margulis M, Shi QY, Fielding A. Saturation of postsynaptic glutamate receptors after quantal release of transmitter. Neuron. 1994;13:1385–1393. doi: 10.1016/0896-6273(94)90423-5. [DOI] [PubMed] [Google Scholar]
- 63.Trussell LO, Zhang S, Raman IM. Desensitization of AMPA receptors upon multiquantal neurotransmitter release. Neuron. 1993;10:1185–1196. doi: 10.1016/0896-6273(93)90066-z. [DOI] [PubMed] [Google Scholar]
- 64.van der Kloot W. Estimating the timing of quantal releases during end-plate currents at the frog neuromuscular junction. J Physiol (Lond) 1988a;402:595–603. doi: 10.1113/jphysiol.1988.sp017224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.van der Kloot W. The kinetics of quantal releases during end-plate currents at the frog neuromuscular junction. J Physiol (Lond) 1988b;402:605–626. doi: 10.1113/jphysiol.1988.sp017225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.von Gersdorff H, Schneggenburger R, Weis S, Neher E. Presynaptic depression at a calyx synapse: the small contribution of metabotropic glutamate receptors. J Neurosci. 1997;17:8137–8146. doi: 10.1523/JNEUROSCI.17-21-08137.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wang LY, Kaczmarek LK. High-frequency firing helps replenish the readily releasable pool of synaptic vesicles. Nature. 1998;394:384–388. doi: 10.1038/28645. [DOI] [PubMed] [Google Scholar]
- 68.Weis S, Schneggenburger R, Neher E. Properties of a model of Ca++-dependent vesicle pool dynamics and short term synaptic depression. Biophys J. 1999;77:2418–2429. doi: 10.1016/S0006-3495(99)77079-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wright SN, Brodwick MS, Bittner GD. Calcium currents, transmitter release and facilitation of release at voltage clamped crayfish nerve terminals. J Physiol (Lond) 1996;496:363–378. doi: 10.1113/jphysiol.1996.sp021691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wu LG, Borst JG. The reduced release probability of releasable vesicles during recovery from short-term synaptic depression. Neuron. 1999;23:821–832. doi: 10.1016/s0896-6273(01)80039-8. [DOI] [PubMed] [Google Scholar]
- 71.Wu LG, Westenbroek RE, Borst JGG, Catterall WA, Sakmann B. Calcium channel types with distinct presynaptic localization couple differentially to transmitter release in single calyx-type synapses. J Neurosci. 1999;19:726–736. doi: 10.1523/JNEUROSCI.19-02-00726.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Xu T, Rammner B, Margittai M, Artalejo AR, Neher E, Jahn R. Inhibition of SNARE complex assembly differentially affects kinetic components of exocytosis. Cell. 1999;99:713–722. doi: 10.1016/s0092-8674(00)81669-4. [DOI] [PubMed] [Google Scholar]
- 73.Zucker RS. Calcium- and activity-dependent synaptic plasticity. Curr Opin Neurobiol. 1999;9:305–313. doi: 10.1016/s0959-4388(99)80045-2. [DOI] [PubMed] [Google Scholar]