Release-Independent Short-Term Synaptic Depression in Cultured Hippocampal Neurons (original) (raw)
Abstract
Short-term synaptic plasticity may dramatically influence neuronal information transfer, yet the underlying mechanisms remain incompletely understood. In autapses (self-synapses) formed by cultured hippocampal neurons, short-term synaptic depression (STD) had several unusual features. (1) Reduction of neurotransmitter release probability with Cd2+, a blocker of voltage-gated calcium channels, did not change depression. (2) Lowering [Ca2+]o and/or raising [Mg2+]o had little effect on STD in cells with strong baseline depression, but in cells with more modest baseline depression, it reduced the depression. (3) Random variations in the size of initial EPSCs did not influence successive EPSC sizes. These findings were inconsistent with release-dependent mechanisms, such as vesicle depletion, post-synaptic receptor desensitization, and autoreceptor inhibition. Instead, other results suggested that changes in action potentials (APs) contributed to depression. The somatic APs declined in amplitude with repetitive stimulation, and modest reduction of AP amplitudes with tetrodotoxin inhibited EPSCs. Notably, tetrodotoxin also increased depression. Similar changes in axonal APs could produce STD in at least two ways. First, decreasing presynaptic spike amplitudes could reduce calcium entry and release probability. Alternatively, APs could fail to propagate through some axonal branches, reducing the number of active synapses. To explore these possibilities, we derived the expected variance of EPSCs for the two scenarios. Experimentally, the variance increased and then decreased on average with successive responses during trains of APs, confirming a unique prediction from the conduction failure scenario. Thus, STD had surprising properties, incompatible with commonly postulated mechanisms but consistent with AP conduction failure at axonal branches.
Keywords: short-term synaptic plasticity, short-term synaptic depression, autapse, microisland, cell culture, hippocampus, cadmium, calcium, magnesium, correlation analysis, miniature EPSC, action potential, tetrodotoxin, variance analysis, simulation, branch-point failure, conduction failure, propagation failure
Short-term synaptic plasticity (STP) refers to the changes in the efficacy of synaptic transmission that occur from one action potential to the next, depending on the recent history of presynaptic activity. Such plasticity, lasting from milliseconds to seconds, is believed to figure importantly in neuronal information transfer (Magleby, 1987; Zucker, 1989; Markram and Tsodyks, 1996; Abbott et al., 1997; Tsodyks and Markram, 1997). The transient alterations in synaptic efficacy can be richly diverse in manifestation, taking the form of short-term facilitation and/or depression (Zucker, 1989), with more than one mechanism sometimes present at an individual synapse (Thomson and West, 1993; Thomson, 1997; Varela et al., 1997). Moreover, synapses from the same presynaptic neuron onto different postsynaptic targets may have different types of short-term plasticity (Thomson and Deuchars, 1994;Reyes et al., 1998). Such plasticity is widespread, and there is considerable interest in its causes, theoretical significance, and physiological roles.
Much of what is known about short-term synaptic plasticity has come from experiments in brain slice preparations, which have been essential in defining its physiologically important features. But polysynaptic circuits, incomplete solution exchange, and the small sizes of individual synaptic responses in slices may complicate investigation of the mechanisms underlying plasticity. Cultured neuronal preparations may therefore be an important complement for in-depth investigations into the sources of STP. Hippocampal neurons grown in culture on glial microislands form synapses onto themselves (Furshpan et al., 1986;Bekkers and Stevens, 1991), termed autapses (Van der Loos and Glaser, 1972). These autaptic circuits are by definition monosynaptic, solution exchanges can be fast and complete, and the synaptic responses are large and robust. Previously, prominent short-term depression (STD) has been observed in such neurons under normal conditions (Mennerick and Zorumski, 1995), which seems to mimic the short-term plasticity between pairs of CA1 pyramidal cells (Deuchars and Thomson, 1996), but is unlike the facilitation that occurs in other hippocampal synapses (Lomo, 1971; Alger and Teyler, 1976).
We have recently used these microcultured hippocampal neurons to provide evidence for a novel form of short-term synaptic facilitation attributable to relief of G-protein inhibition of presynaptic calcium channels (Brody and Yue, 2000). In the course of these experiments, it became clear that the short-term synaptic depression present at baseline without G-protein inhibition had unusual features. In particular, the depression seemed to be release-independent, meaning that when we pharmacologically lowered presynaptic release probability, the depression did not diminish proportionally. Instead, many previously reported forms of short-term depression are release-dependent, consistent with commonly proposed mechanisms in which each release event depletes some limiting resource, such as readily releasable synaptic vesicles (Zucker, 1989; Stevens and Tsujimoto, 1995; Tsodyks and Markram, 1997). Here, we investigated the mechanism of the release-independent depression in single, cultured hippocampal neurons, using a combination of pharmacological manipulations, analysis of EPSC variances, and modeling. Our results are most consistent with depression arising, at least in part, from failures of the action potential to propagate along axonal branches.
MATERIALS AND METHODS
Cultured neurons. Hippocampal neurons were cultured on glial microislands essentially as reported (Furshpan et al., 1986;Bekkers and Stevens, 1991). Briefly, 9 × 9 mm glass coverslips were acid-cleaned, ethanol-sterilized, and placed in six-well culture dishes (Beckton Dickinson, Franklin Lakes, NJ). A 0.15% agarose solution was spread uniformly on the slips to provide a hydrophobic, nonadhesive background. Then a solution containing 2 mg/ml poly-d-lysine, 3 mg/ml collagen (Cellprime, Collagen Corporation, Palo Alto, CA) and 8.5 mm acetic acid was sprayed onto the plates using an airbrush (Aztek, Rockford, IL) fitted with a spatter nozzle to make 50- to 750-μm-diameter “islands” of adhesive substrate. After drying and UV-sterilization, cultured astrocytes left over from a previous preparation (see below) were trypsinized and plated at a density of 6,000–24,000 cells per milliliter in FCS media. FCS media was MEM with Earle's salts (Life Technologies, Grand Island, NY) plus 10% fetal calf serum, 20 mm glucose, 0.5% N2 supplement (Life Technologies), 0.5% penicillin/streptomycin stock, and phenol red. After 4–6 d at 37°C in 5% CO2, the astrocytes spread out over the microislands but did not grow on the agarose. FCS media was replaced with NEU media to allow the astrocytes to condition the media before the arrival of the neurons. NEU media contained MEM with Earle's salts and 25 mm HEPES (Life Technologies), 10% horse serum (Life Technologies), 20 mm glucose, 1% N2 supplement, 1 mm sodium pyruvate, 0.5% penicillin/streptomycin stock, and 0.875 μg/ml biotin. All media was equilibrated at 37°C in 5% CO2 before use.
The next day, neonatal (1–2 d old) Sprague Dawley rats were decapitated, and their brains were placed in ice-cold Earle's Balanced Salt Solution (EBSS, Life Technologies) with 10 mm HEPES. Oblique razor cuts were made from the anterior midline to the posterior temporal lobe, exposing portions of the hippocampi enriched in CA1 and CA3 neurons. The meninges were gently removed starting from the rostral end, and in the process, the exposed wedge of hippocampus flipped out of the bowl formed by the lateral ventricle. The tissue was further enriched in CA1 and CA3 pyramidal cells by clipping away a central portion of dentate gyrus that sometimes remained with the hippocampal wedge. Selective dissection of CA1 and CA3 increased the number of glutamate-releasing pyramidal cells relative to inhibitory interneurons. The tissue was minced into 1 mm3pieces and digested in papain solution at 37°C for 50 min. Papain solution contained 20–25 U/ml papain (Worthington, Lakewood, NJ), 1 mm CaCl2, 0.5 mm EDTA, and 10 mm HEPES in EBSS, and was prewarmed to 37°C. DNAase (Calbiochem, San Diego, CA) was added to 0.1 μg/ml for 5 min further incubation. Then the tissue was washed twice with FCS media, triturated in NEU media, and passed through a 70 μm cell strainer (Beckton Dickinson) to isolate single cells. The cells were plated onto the astrocyte-containing microislands at a range of densities between 2,000 and 28,000 per milliliter. Usually one of these densities yielded a significant number of islands containing a single neuron. Plating onto astrocytes improved the health and longevity of the neurons and dramatically enhanced the number and strength of synapses that they formed. The day after plating, the proliferation of astrocytes was halted by adding 35 μm 5-fluoro-2-deoxyuridine (Sigma, St. Louis, MO) with 75 μm uridine. Patch-clamp recordings were made between 7 and 21 d in vitro. Media did not need to be exchanged for up to 21 d.
Leftover cells were placed in FCS media in an uncoated tissue culture flask. After 7 d, the flask was shaken on a laboratory shaker overnight at room temperature, and then the media was replaced. This rough treatment killed process-bearing and sensitive cells such as neurons and created a purified astrocyte culture. If fibroblasts were present, the culture was discarded.
Electrophysiology. Microislands containing one or more glia and a single neuron with extensive processes were selected for whole-cell patch-clamp recording. Pipets with resistance of 3–4 MΩ were pulled from borosilicate glass (TW150F-4, WPI, Sarasota, FL) and lightly fire-polished. Standard pipette solution contained (in mm): 137 K-gluconate, 12 NaCl, 10 HEPES, 4 EGTA, 0.5 CaCl2, 4 MgATP, and 0.3 LiGTP, pH 7.2 with KOH. Standard extracellular solution contained (in mm): 145 NaCl, 5.4 KCl, 2 CaCl2, 1 MgCl2, 10 HEPES, pH 7.4 with NaOH, adjusted to 310 mOsm with 15–25 mm glucose. All chemicals were from Sigma except NBQX from RBI (Natick, MA). Solutions were exchanged via gravity-fed lines connecting to a 1-mm-diameter glass tube placed 0.5 mm from the cell under study. Solutions flowed continuously at a rate of ∼1 ml/min. A junction potential of −14 mV was corrected before sealing. All recordings were made at room temperature (23–25°C).
Data were acquired using an Axopatch 200B (Axon Instruments, Foster City, CA) patch-clamp amplifier and a DEC PDP-11 computer running custom software written in Basic 23. In voltage-clamp mode, the holding potential was −80 mV, and propagating action potentials were stimulated with either 2 msec voltage steps to +20 mV or 1.5 msec wide action potential waveforms reaching +30 mV from a baseline of −80 mV. Sampling intervals were 40–50 μsec, and filtering was at 5 kHz. Series resistance was typically 6–10 MΩ and was compensated 50–85% when possible. In some cells, series resistance compensation caused electrical ringing and was not used. After initial breakthrough into whole-cell mode, EPSCs stabilized in 3–5 min. Thereafter, data traces were acquired every 15–30 sec. Rundown, or decreases in EPSC amplitude over tens of minutes, occurred in some cells, even with data traces acquired every 30 sec. Rundown, however, did not affect any aspect of short-term synaptic plasticity in any significant way (data not shown). Whenever EPSC amplitudes in two conditions were compared, measurements were made in both conditions within 5–10 min of each other to minimize the effects of rundown.
For current-clamp recordings, the fast mode of the Axopatch 200B was used. Baseline current injection was typically <100 pA, and adjusted to maintain a resting potential near −80 mV. Action potentials were stimulated by injection of 0.3 to 0.8 nA current pulses lasting 2 msec. NBQX (2 μm) was included during all such experiments to eliminate EPSPs.
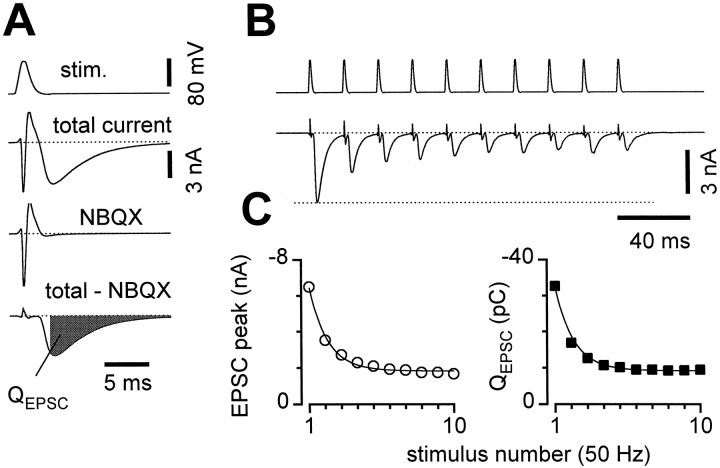
Analysis. In each cell with excitatory synaptic transmission, the EPSCs mediated by AMPA-type glutamate receptors were defined as the current sensitive to 2–5 μm of the AMPA receptor antagonist NBQX. Total EPSC charge transfer in windows extending 2–3 to 20 msec after each stimulus was calculated by integrating currents in this window and subtracting integrals of NBQX-resistant currents from the same cell in the same time window. NBQX-resistant currents were generally smaller than 10% of basal EPSC size and stable over time. In displayed traces, NBQX-insensitive currents have been subtracted from total currents, and 2–3 msec stimulus transients have been blanked for clarity except in Figure1.
Fig. 1.
Short-term depression (STD) in microcultured hippocampal neurons. A, Voltage-clamp stimuli (stim.) were applied via a somatic patch pipette to single self-synaptic (autaptic) neurons in culture, and the resulting currents were recorded (total current). Synaptic currents were isolated by subtracting the current remaining in 2 μmNBQX (NBQX), from the total current (total − NBQX), and integrated over a 3–20 msec window after each stimulus (QEPSC). B, Isolated synaptic currents during a 50 Hz train of voltage-clamp stimuli.C, Both peak current (left) and_Q_EPSC (right) equivalently represented the short-term depression. After scaling, the smooth monoexponential curve (time constant 22.5 msec) fit to peak currents (left) exactly described depression of_Q_EPSC (right, scaling by ∼5 pC/nA for this cell). Averages of 14 sweeps from the same cell as in_A_ and B; error bars are smaller than symbols.
For very short interstimulus intervals, the first EPSC was still decaying during the second EPSC. To calculate the true amplitude of the second EPSC, we subtracted the expected contribution of the first EPSC to the total current in the second EPSC's integration window. Measurements of short-term synaptic plasticity were obtained by averaging 5–20 sweeps and normalizing by the amplitude of the first EPSC. This analysis was performed using custom software written in Matlab (The MathWorks, Natick, MA). Somatic action potential amplitudes and widths were measured automatically also using custom software written in Matlab.
All averages, variances, and statistical comparisons were calculated with Microsoft Excel. The p values given in the text were obtained from two-tailed, paired t tests or from two-tailed, unequal variance t tests as appropriate. Error values (±) cited in the text are standard errors. To check the stability of EPSCs over time (see Figs. 5, 9), we used the regression macro from the Microsoft Excel 7.0 Data Analysis tools. Data were accepted as sufficiently stable if the regression slope 95% confidence interval included zero. To look for inverse correlations between the first and second EPSCs for both simulated and experimental data (see Fig. 5), the same correlation tool was used. Final correlation coefficients were calculated after excluding rare outlying sweeps (16/431) with first EPSCs more than 3 SDs away from the means for their respective cells. Similar conclusions were reached before these exclusions.
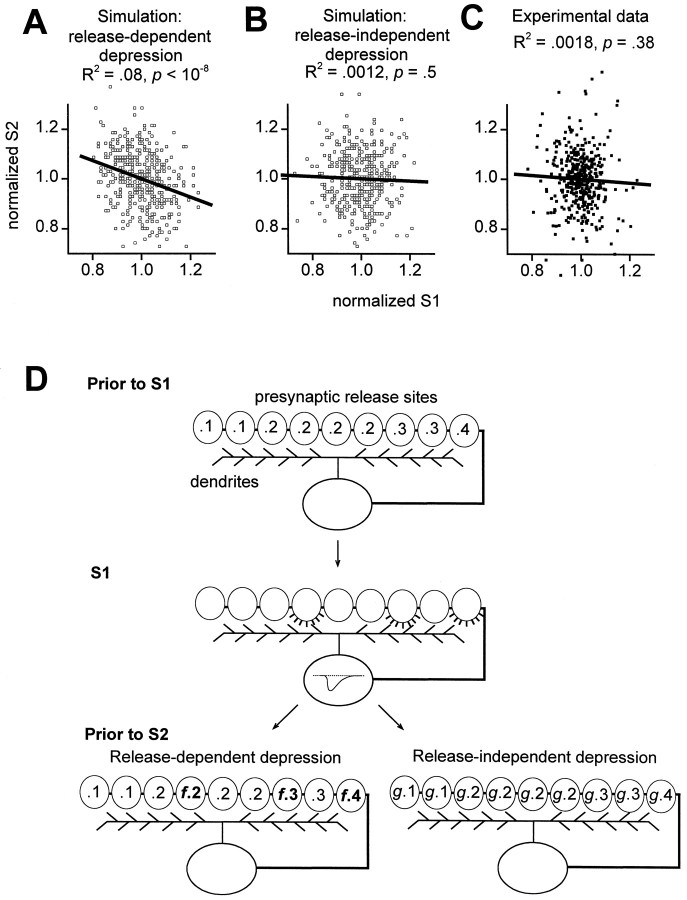
Fig. 5.
Sweep-to-sweep fluctuations in first EPSC sizes did not affect second EPSCs. For both simulations and experimental data, each first _Q_EPSC was normalized by the first _Q_EPSC average (normalized S1) and each second _Q_EPSC was normalized by the second Q_EPSC average (normalized S2).A, Simulation of release-dependent depression. Four hundred pairs of EPSCs were generated using a model with 500 binary release sites (see Materials and Methods). There was a significant inverse correlation between successive, normalized EPSC sizes (open squares, individual simulated EPSC pairs; solid line, linear regression). Regression slope was −0.37, with 95% confidence interval −0.49 to −0.25. B, Simulation of release-independent depression. There was no correlation here between successive normalized EPSC sizes. C, Experimental data; 415 sweeps in control solutions (solid squares) taken from 28 stable cells were normalized for each cell and then pooled. No significant correlation between normalized first and second EPSC sizes; the slope of the best fit regression line through the data was −0.074, with 95% confidence interval −0.24 to 0.09. D, Simplified illustration of release-dependent versus release-independent depression mechanisms used in simulations. Before the first stimulus (Prior to S1), autaptic release sites (ovals) had nonuniform release probabilities (numbers inside ovals). With the first stimulus (S1) some sites released (fourth, seventh, and ninth sites from_left). With short-term synaptic depression, the net efficacy of the synapses was then decreased (Prior to S2). For release-dependent depression (left), the sites that released on S1 had their release probabilities reduced (multiplied by f < 1), whereas other sites were unchanged. For release-independent depression (right), all sites had their release probabilities reduced (multiplied by g < 1).
Fig. 9.
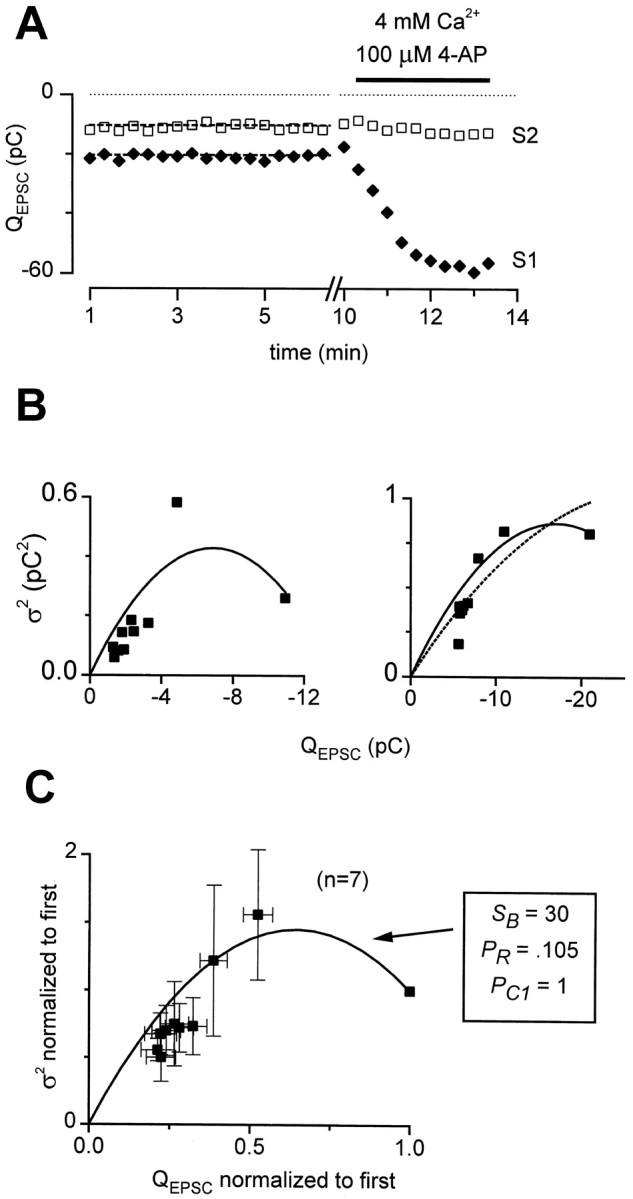
Experimentally measured EPSC variances during STD.A, Demonstration of acceptance criteria for variance measurements. Seventeen first and second EPSCs (solid diamonds, S1 and open squares,S2) were stable in amplitude over time (dashed lines: slope = 0). EPSCs were 2.7-fold larger in 4 mm Ca2+ plus 100 μm 4-AP, constraining initial PR to <0.37.B, _Q_EPSC variance (ς2) versus _Q_EPSC mean during STD for two representative cells. Left, Clear increase and decrease in variance with STD. Solid line, Fit to Equation 2, the axonal conduction failure formula, with initial conduction probability (PC1) constrained to 1, SB = 8.29, PR = 0.32, NB = 111, and q = −0.038 pC. Data from 16 sweeps.Right, No clear rise in variance with depression. Nonetheless, a better description of the data was provided by Equation2 with PC1 constrained to 1, SB = 6.06, PR = 0.21, NB = 447, and q = −0.042 pC than by the binomial variance formula with N = 809, _P_Rinitially = 0.37, and q = −0.072 pC. Data were from 18 sweeps. C, Average mean–variance relation. For seven cells that met acceptance criteria, both EPSC means and variances derived from 10–18 sweeps per cell were normalized by their initial values and averaged across cells. Equation 2 was fit to these averaged data as detailed in Materials and Methods, with parameters as shown. Multiple linear regression analysis of variance versus mean and mean2 yielded a nearly identical fit, with R2 = 0.866 and p values for coefficients of the mean and mean2 of 3 × 10−8 and 2.5 × 10−7, respectively.
The fits of mean versus variance data were performed using the Microsoft Excel 7.0 Solver tool, with the constraint that the fit had to include the data point corresponding to the initial mean and variance. In fitting the average normalized data to Equation 2 (see Fig. 9C), the parameters N and q were dropped, because they cannot be constrained by normalized data. The variance contributed by NBQX-insensitive currents was not subtracted from the total variance, because it was always <5% of the total variance and did not change with repetitive stimulation.
Simulations of correlations between pairs of EPSCs (see Fig.5). Simulations were performed to assess our ability to experimentally resolve correlations that would result if release-dependent paired-pulse depression (PPD) were present (see Fig.5). In principle, release-dependent depression should produce inverse correlations between the sizes of successive EPSCs, whereas release-independent depression should not produce any such correlations (Thomson et al., 1993; Debanne et al., 1996). For example, an inverse correlation means that a relatively large first EPSC would be followed more often than not by a relatively small second EPSC, and vice versa.
For each simulated EPSC the contributions from 500 model release sites were summed. We estimated that cultured autapses contained at least 500 sites from measurements of average EPSC amplitude (2000 pA), average quantal amplitude (15 pA), and upper-limit estimate of release probability [0.29, see Fig. 9A: 2000 pA/(15 pA × 0.29) ≈ 500]. Each release site was assumed to release either no vesicle or one vesicle with each stimulus, and quantal amplitudes were considered to be uniform. Because the results of interest were always relative EPSC sizes, quantal amplitudes were arbitrarily set to 1. For each simulation, we generated a new group of 500 heterogeneous initial release probabilities, which were drawn from a γ distribution with parameters similar to those found experimentally in slices and cultured neurons (Dobrunz and Stevens, 1997; Murthy et al., 1997). To calculate the size of a simulated EPSC, a uniform random number between 0 and 1 was generated for each of the 500 model release sites. A site released successfully if the random number was less than its release probability and the simulated EPSC amplitude was equal to the number of successful releases. Other distribution parameters were also explored with the constraint that the mean initial release probability was always <0.5, to accord with experimental results (see Fig.9A). These simulations yielded results similar to those displayed in Figure 5 (data not shown).
In simulations of PPD attributable to a release-dependent mechanism, if a given individual site successfully released on the first stimulus, its probability of releasing on the second stimulus was set to be a small, constant fraction (f) of its original release probability. If it did not release, its release probability was unchanged on the second trial. In release-independent depression, the release probability was decreased uniformly at all sites before the second stimulus. For each correlation trial, we generated 400 pairs of EPSCs, one with the initial set of release probabilities and the second using the modified release probabilities after depression. In the release-dependent depression simulations shown in Figure 5A, we used an f value of 0.02. Initial release probabilities were drawn from a γ distribution that peaked at a release probability of 0.1, with an exponent of 2. These parameters yielded an initial mean release probability of 0.2 and paired-pulse depression of 30.4% (paired-pulse modulation 0.696), similar to experimental data (see Fig. 3).
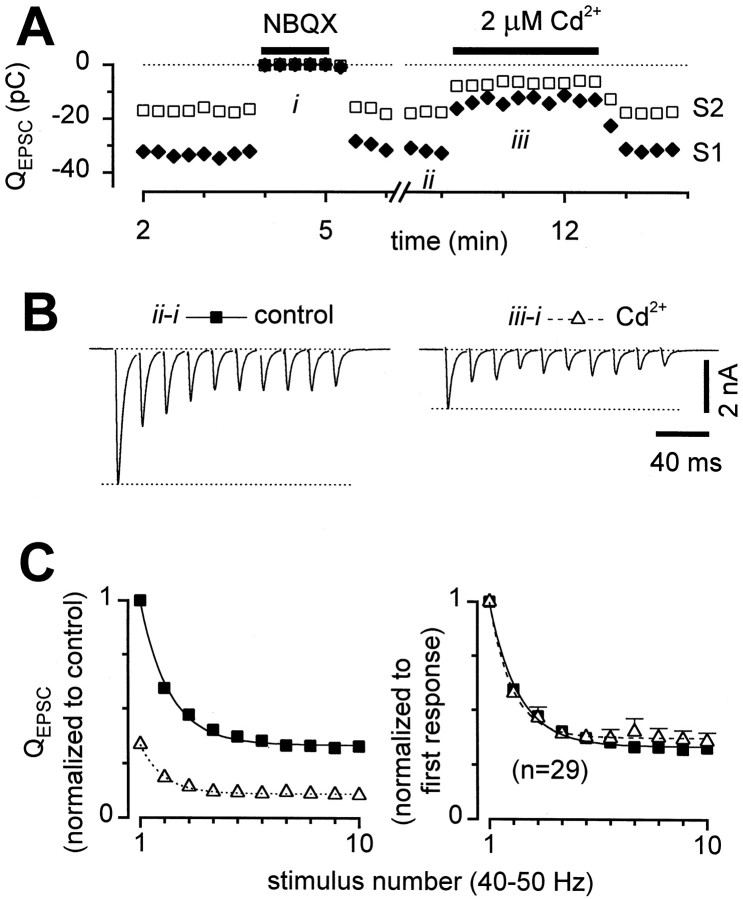
Fig. 3.
STD was not affected by reduction in release probability by Cd2+. A, Diary plot of_Q_EPSC for first stimuli (solid diamonds, S1) and second stimuli (open squares, S2) of 50 Hz stimulus trains. Both NBQX and Cd2+ were readily reversible. B, Sample records after NBQX subtraction, acquired at the times indicated by_ii_ and iii in the diary plot above. C,_Q_EPSC averages across 29 cells. Left, Responses normalized by the first _Q_EPSC in control (solid squares) for each cell, then averaged across cells, showing extent of inhibition by Cd2+(open triangles). Right, Responses normalized by first _Q_EPSC in each condition, to facilitate comparison of STD. There were no statistically significant differences between control and Cd2+. Error bars not shown when smaller than symbols. Time constant of smooth curve was 23.8 msec.
To address the question of how sensitive the correlation method used in Figure 5 was in detecting release-dependent depression, we performed a series of simulations with varying values of f. We increased f, decreasing the overall amount of release-dependent depression, until the statistical significance of the negative correlations approached our cutoff of p = 0.05. This cutoff was approached at f = 0.5, where the overall paired-pulse depression was 14.4 ± 0.17% (n = 11 simulations), and the p values for the slopes of the regression lines were between 0.00053 and 0.067 (mean 0.017). Thus, the correlation method was sensitive enough to detect much smaller amounts of release-dependent depression than were shown in Figure5A, or in the electrophysiological data (32%).
Variance calculations for action potential conduction failure (see Figs. 8, 9). For derivations of analytical relations for homogeneous values of parameters used in Figures 8, A and_B_, and 9, see .
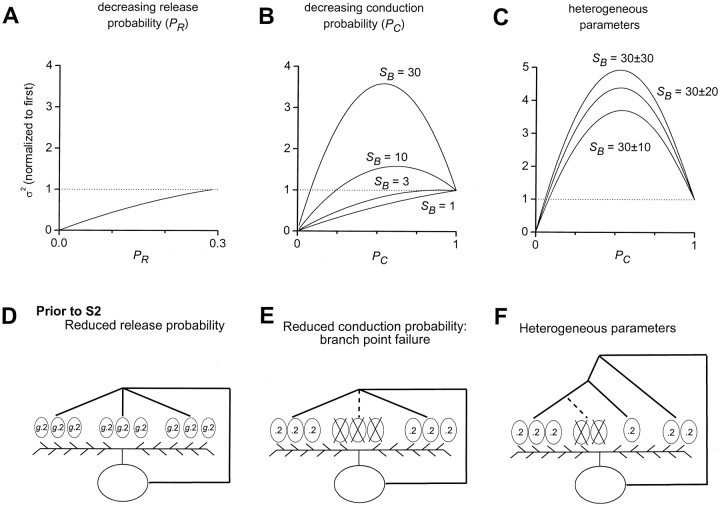
Fig. 8.
Expected EPSC variance in two models of release-independent STD. A, Depression attributable to decreasing release probability (PR) at each vesicle release site. Variance fell monotically with decreasing PR when initial PR was constrained to be <0.29 (see Results). Curve plotted according to the binomial variance formula, ς2 = NPR(1 − PR).B, Depression attributable to decreasing action potential conduction probability (PC) through axonal branches. Variance could fall monotically, or rise and then fall with decreasing PC, depending on the number of release sites per axonal branch (SB). Curves plotted according to Equation 2, with PR = 0.29 and initial conduction probability (PC1) constrained to 1. N and q do not affect the normalized variance. C, Depression attributable to decreasing PC with heterogeneity in axonal branch properties. Populations of 500 axonal branches with heterogeneous numbers of sites per branch (SB). SB values were drawn from a normal distribution with mean 30 and SDs between 10 and 30 as labeled. In addition, the rate of decrease in PC was also heterogeneous across branches, with mean 0.2 and SD 0.05 (see Materials and Methods). Mean–variance relations were nearly parabolic, with clear rise and fall in variance with depression of the mean. D, Simplified illustration of depression attributable to reduced release probability. Similar format as in Figure 5D except that all release sites had the same initial release probability. E, Depression attributable to reduced axonal conduction probability at axonal branches. In this illustration, action potential failed to propagate through center branch, effectively removing three release sites. Release probabilities were unchanged at other sites. F, Schematic representation of heterogeneous axonal branch properties. Note range of numbers of release sites per branch and variety in axonal branching complexity. Axonal branching complexity represents one potential mechanism underlying heterogeneous conduction probabilities through terminal branches (see Materials and Methods).
To explore the effects of relaxing some of the simplifying assumptions used in the , we numerically calculated the means and variances for populations of heterogeneous axonal branches (i.e., see results in Fig. 8C). For each simulation, we considered a population of 50–500 independent axonal branches and picked a random value for the number of sites per branch (SB) from a distribution of values. The distribution used was a clipped normal distribution, with SDs less than or equal to the value of the mean. Distributions were clipped in that values below 0 were taken to be equal to 0, and values above two times the mean were taken to be equal to two times the mean. To simulate depression attributable to conduction failures, conduction probabilities at each branch were decreased in discrete time steps. The rates of decrease were also heterogeneous and drawn from clipped normal distributions. These rates were held constant for each time step and were not correlated with the values of SB. The total mean and variance were calculated at each time step by calculating the mean and variance for each branch, according to Equation EA6 in the , and summing across branches. Smooth curves displayed in Figure 8C were generated by interpolating between time steps. Release probabilities and quantal sizes were uniform across release sites, initial conduction probability (PC1) was set at 1, and all results were normalized by the initial values of mean and variance.
The heterogeneous rates of decrease in PC were used as a general representation for several possible scenarios. Differences between branches could arise from the variability in axonal dimensions or in the electrical excitability of the branch points. Similarly, variability in the axonal branching complexity could contribute to nonuniform depression of conduction probability. For example, even if all individual axonal branch points were equivalent, groups of release sites located distal to several sequential branch points would have lower total conduction probability than those found more proximally (see Fig. 8F).
RESULTS
Characteristics of short-term depression
Single, glutamatergic hippocampal neurons grown in culture on glial microislands were chosen for analysis of short-term depression. To record postsynaptic currents, we delivered brief voltage-clamp stimuli via a somatic, whole-cell patch pipette (Fig.1A, top). Propagating action potentials were generated, with momentary loss of voltage-clamp control caused by large sodium and potassium currents corresponding to initial inward and outward currents. Slower inward currents followed, which flowed through AMPA-type glutamate receptors (Fig. 1A, total current). Subtraction of responses obtained with the AMPA antagonist NBQX (Fig.1A, NBQX) isolated synaptic currents (Fig. 1A, total − NBQX). These EPSCs were quantitated by integrating over a 3–20 msec window after each stimulus (Fig. 1A,QEPSC). Isolated synaptic currents were recorded with good voltage-clamp control, as they had an extrapolated reversal potential near 0 mV and their kinetics were unchanged in subsaturating concentrations of NBQX that reduced the sizes of the synaptic currents (data not shown) (Bekkers and Stevens, 1991).
During 50 Hz trains of stimuli, short-term synaptic plasticity under control conditions was dominated by depression (Fig.1B), similar to previous findings (Mennerick and Zorumski, 1995). Short-term synaptic facilitation was rarely apparent, likely because of the high intracellular EGTA that we used to chelate residual calcium (see Materials and Methods; our unpublished observations). The EPSCs declined to ∼60% of their original size on the second stimulus of the trains and to ∼30% by the 10th stimulus. Measurements of either the EPSC peaks or integrals (_Q_EPSC) yielded quantitatively indistinguishable results for the extent of depression (Fig.1C). For the remainder of the analyses, EPSC integrals were preferred because they more reliably included the contributions of slightly asynchronous release events.
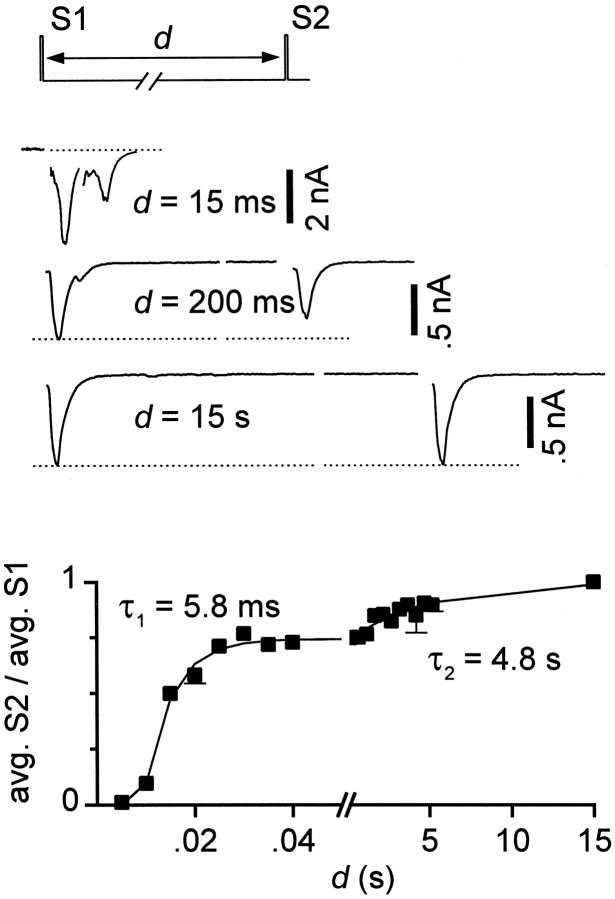
The recovery from synaptic depression followed an apparently biexponential time course (Fig. 2), also consistent with a previous report (Mennerick and Zorumski, 1995). The time constants of recovery were 8.9 ± 2.3 msec (_n_= 9) and 4.3 ± 0.42 sec (n = 6). During the 20 msec intervals between stimuli at 50 Hz, the fast component of recovery was not complete, and therefore the extent of spike-to-spike depression reflected contributions from both of the resolvable kinetic components.
Fig. 2.
Recovery from depression occurred in two phases. Interstimulus interval (d) between pairs of stimuli (S1, S2) was varied between 5 msec and 15 sec. Shown are single sweeps for intervals of 15 msec, 200 msec, and 15 sec (top). _Q_EPSC averages after second stimuli (avg. S2) were normalized by_Q_EPSC averages after first stimuli (avg. S1). Five to ten sweeps were averaged for each interstimulus interval. Error bars not shown when smaller than symbols. The sum of two exponentials (smooth curve) was fit to the recovery of the EPSCs (avg. S2/avg. S1); for this cell, time constants were 5.8 msec and 4.8 sec, with relative amplitudes 0.74 and 0.26.
To determine whether a release-dependent mechanism underlies the observed STD, we investigated the effects of reducing presynaptic calcium entry with Cd2+, a blocker of voltage-gated calcium channels. Cd2+ blocks at micromolar concentrations, so surface charge effects are minimal, and there is no significant change in the relative current–voltage relations of the channels (Leonard et al., 1987; Hanck and Sheets, 1992). Cd2+ (2 μm) had no resolvable effect on the size of miniature EPSCs (n = 4 cells; data not shown) or on somatic action potentials (n = 5 cells) (Brody and Yue, 2000), confirming that Cd2+ effects were entirely presynaptic. Hence, Cd2+ blockade may be a particularly clean method of reducing presynaptic calcium entry. Addition of 2–4 μm Cd2+ to the external solution reduced _Q_EPSC to ∼40% of its size in control (Fig. 3). The depression during trains, however, was unchanged in most individual cells (Fig. 3B) and on average across cells (Fig.3C), although in rare recordings (3 of 29) there was somewhat less depression in Cd2+. Thus the extent of synaptic depression did not typically appear to be related to initial release probability, making release-dependent mechanisms such as vesicle depletion unlikely.
In a previous report, depression in a very similar preparation was altered by changing extracellular calcium and magnesium concentrations (Mennerick and Zorumski, 1995), which did seem consistent with a release-dependent mechanism. This apparent contradiction could arise because the effects of Cd2+ may differ from those of changing [Ca2+]o and [Mg2+]o. Millimolar alterations in Ca2+ and/or Mg2+ concentrations may alter surface charge screening, which would change the voltage sensitivity of voltage-gated channels, and thereby affect overall membrane excitability (Frankenhaeuser and Hodgkin, 1957; Green and Andersen, 1991). Alternatively, other aspects of the techniques and preparations may differ.
To examine the basis of this apparent discrepancy, we also lowered release probability using a variety of different [Ca2+]o and [Mg2+]o solutions (ΔCa/Mg). All solutions reduced initial EPSC amplitudes, as expected, but detailed consideration of the effects of these manipulations on STD proved complex. In some cells, ΔCa/Mg did not affect depression (e.g., Fig.4A, cell 1). In other cells, the same solutions similarly inhibited the first EPSCs, yet depression was reduced (e.g., Fig. 4A, cell 2). Similar variable effects were found for a variety of different solutions, including (in mm): 0.5 Ca/1 Mg, 1 Ca/2 Mg, 1 Ca/4 Mg, 1.25 Ca/1 Mg, and 2 Ca/10 Mg. However, on average, differences became apparent for the effects of the various solutions on depression (Fig. 4B). STD was unchanged on average in 1.25 Ca/1 Mg, mildly affected in 1 Ca/2 Mg, and almost eliminated in 1 Ca/4 Mg (Fig. 4B). The 1.25 Ca/1 Mg and 1 Ca/2 Mg solutions both inhibited initial EPSCs ∼60%, whereas 1 Ca/4 Mg inhibited ∼85%. The lack of change in STD with 1.25 Ca/1 Mg further supported our hypothesis that depression was release independent. Attenuation of STD with elevations in [Mg2+]o in general could be consistent with effects on membrane excitability caused by surface charge screening or alterations in calcium-regulated conductances (see Discussion). However, the results of other manipulations fit imperfectly with this overall notion; 0.5 Ca/1 Mg was similar to 1 Ca/4 Mg (n = 5), and 2 Ca/10 Mg had little effect on STD (n = 2).
Fig. 4.
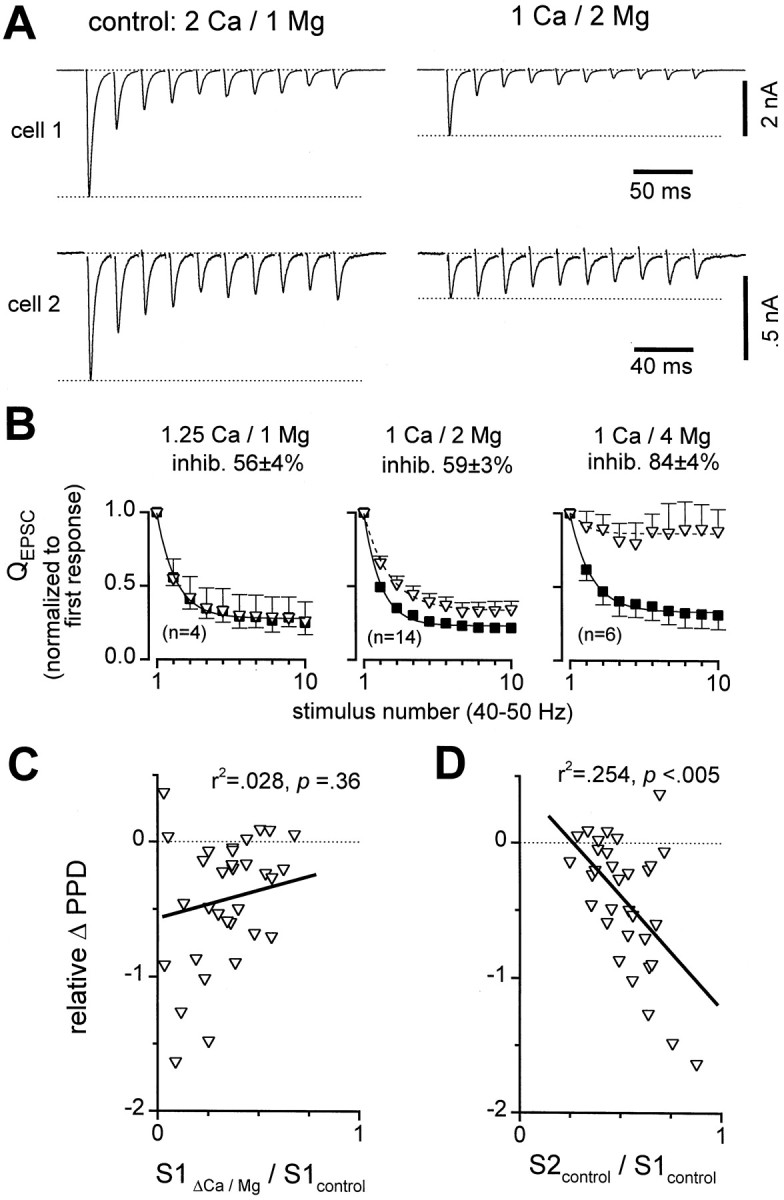
Complex effects on depression with reduced [Ca2+]o and/or increased [Mg2+]o (ΔCa/Mg). A, Sample records from two cells, illustrating diverse effects of 1 Ca/2 Mg solution. In both cells 1 Ca/2 Mg reduced initial EPSCs, but depression in cell 1 was unchanged while depression in_cell 2_ was reduced. Averages of four to nine traces displayed. B, Average effects of three different solutions. Control _Q_EPSC responses were normalized by first response in control for each cell and averaged across cells (solid squares). Each ΔCa/Mg _Q_EPSCwas normalized by first response in ΔCa/Mg before averaging across cells (open triangles). Inhib. refers to the average decrease in size of _Q_EPSC after first stimuli in ΔCa/Mg compared with control. C, D, Multiple regression analysis of relative change in paired-pulse depression (relative ΔPPD) correlated with two factors:_Q_EPSC size in ΔCa/Mg relative to control (S1ΔCa/Mg/S1control), and paired-pulse plasticity in control (S2control/S1control). Relative ΔPPD = (PPD in ΔCa/Mg − PPD in control)/PPD in control, where PPD = (S1 − S2)/S1. Data pooled across 31 cells in various ΔCa/Mg solutions; each symbol represents data from one cell, averaged over 5–20 sweeps. Partial correlation coefficients are denoted by r2 values. C, Scatter plot of relative ΔPPD versus initial_Q_EPSC in ΔCa/Mg, normalized by initial_Q_EPSC in control (S1ΔCa/Mg/S1control). There was no significant correlation (solid line) when both factors were considered. D, Scatter plot of relative ΔPPD versus paired-pulse plasticity in control (S2control/S1control). A significant correlation (solid line) was present even when both factors were considered; in cells with strongest baseline depression (S2control/S1control small), the depression was least affected by ΔCa/Mg.
To test whether the effects of ΔCa/Mg were consistent on the whole with release-dependent depression, we pooled all of the data obtained with various ΔCa/Mg solutions and looked for the expected relation between the extent of inhibition in ΔCa/Mg and the changes in depression (Kusano and Landau, 1975). We first noted that many of the cells with the greatest inhibition in ΔCa/Mg (i.e., the smallest values of S1ΔCa/Mg/S1control, where S1 refers to the size of the EPSC evoked by the first stimulus) also showed the largest decreases in paired-pulse depression (Fig. 4C). The greatest decreases in paired-pulse depression correspond to the most negative values of relative ΔPPD in Figure 4,C and D, where PPD was defined as (S1 − S2)/S1 for each condition, and relative ΔPPD was defined as (PPD in ΔCa/Mg − PPD in control)/PPD in control. However, the overall correlation appeared weak, because many cells with significant inhibition by ΔCa/Mg had very little change in depression (Fig.4C). We also recognized another, more robust trend: in cells that had the most baseline depression in control, PPD was hardly affected by ΔCa/Mg (Fig. 4A, cell 1). With weaker baseline depression, ΔCa/Mg had more effect on short-term plasticity (Fig. 4A, cell 2). Regression analysis of data from all cells confirmed this trend (Fig.4D) and revealed a strong correlation between the extent of the baseline depression in control (S2control/S1control) and the changes in depression (relative ΔPPD).
To gauge the relative importance of these two factors, S1ΔCa/Mg/S1control and S2control/S1control, as predictors of relative ΔPPD, we performed multiple regression analysis. This analysis revealed that there was no significant correlation in Figure 4C when the effects of S2control/S1control were included, whereas the correlation in Figure 4_D_remained significant. The apparent relation in Figure 4C was spurious and derived from the strong correlation in Figure4D, coupled through a clear correlation between S1ΔCa/Mg/S1control and S2control/S1control(R2 = 0.15, p < 0.05; data not shown). The lack of genuine correlation between S1ΔCa/Mg/S1control and relative ΔPPD (Fig. 4C) was clearly inconsistent with the presence of release-dependent depression, in agreement with the previous results with Cd2+.
The results with altered Ca2+ and Mg2+ were difficult to interpret in their entirety, but nonetheless, two conclusions could be reliably drawn. First, release-dependent depression cannot account for these effects. Second, there was a robust correlation between the extent of depression and the effects of altering calcium and/or magnesium. On the whole, the data were most consistent with changes in axonal excitability (perhaps because of a combination of surface charge screening and alterations in calcium-regulated conductances) superimposed upon release-independent short-term depression (see Discussion).
We next used an independent method (Fig.5) to further test for the presence of release-dependent STD, taking advantage of the intrinsic fluctuations in the sizes of EPSCs from sweep to sweep (Thomson et al., 1993;Debanne et al., 1996). In the presence of a release-dependent depression mechanism such as vesicle depletion, there should be an inverse correlation between successive, relative EPSC sizes; relatively large first EPSCs should be followed by relatively small second EPSCs, and smaller-than-average first EPSCs should be followed by larger-than-average second EPSCs. Explicit simulation of release-dependent depression in a reasonably sized population of synapses (see Materials and Methods) confirmed that the theoretically expected correlation should be experimentally resolvable (Fig.5A). In this simulation, release probability was reduced by a factor f only in those sites that released successfully, as illustrated in simplified form (Fig. 5D,pathway through left branch). The value of f (0.02) and the distribution of initial release probabilities (mean 0.2) were chosen to yield paired-pulse depression of 30.4%, similar to experimental data (Fig. 3) (see Materials and Methods). This correlation method is sensitive enough to detect release-dependent paired-pulse depression as small as 14.4% (see Materials and Methods). Such correlations have been found experimentally for transmission between pyramidal cells in neocortical and hippocampal slices (Thomson et al., 1993; Debanne et al., 1996). For release-independent depression, however, there should be no such inverse correlation between EPSC sizes (Fig. 5B), and simulations demonstrated that spurious correlations did not arise with experimentally attainable sample sizes. Here, simulated release probabilities were uniformly reduced by a factor g (Fig.5D, pathway through right branch). The presence or absence of this relationship therefore serves as another criterion that can be used experimentally to resolve which of these two general classes of depression predominates.
The correlation analysis for experimental data is shown in Figure5C. We took 415 data sweeps from 28 cells, normalized the response amplitudes for each cell, and then pooled all of the normalized data across cells. All responses used in this analysis were recorded in control 2 Ca/1 Mg solutions. Only groups of at least eight traces in which neither the first EPSC amplitude nor the mean short-term plasticity were changing systematically with time were accepted (see Materials and Methods). In this pooled data, the second EPSC amplitudes were on average 68% of the first EPSC amplitudes. As in the release-independent simulations, there was no correlation between relative first and second EPSC sizes.
To screen for release-dependent depression in a specific subset of cells, we focused our correlation analysis on 6 of the 28 cells that showed the greatest decreases in depression with ΔCa/Mg. These cells had relative ΔPPDs ranging from −0.53 to −1.67. We reanalyzed the correlations between normalized first and second EPSC amplitudes for these six cells individually and for all six pooled. In the analysis of individual cells, there was no significant correlation in five of the six cells. In the sixth, we found a significant negative correlation (slope −1.12, 95% confidence interval −1.88 to −0.36, R2 = 0.46, p = 0.0075). Relative ΔPPD for this cell was in the middle of the range, −0.91. The pooled data from all six cells did not show any significant correlation (slope −0.16, 95% confidence interval −0.56 to 0.23, R2 = 0.006, p = 0.43). Thus we conclude that in general, even for cells with depression that was alleviated when extracellular calcium was lowered, the sorts of correlations expected of release-dependent depression were not present. This further strengthens the evidence that the changes in short-term depression shown in Figure 4 are not a reflection of a release-dependent mechanism, and thus we conclude that the depression is of a release-independent variety.
Presynaptic action potential hypothesis
What sort of mechanism(s) could produce release-independent short-term depression? The source of depression is likely to be presynaptic, given that there were no substantial changes in the size of miniature EPSCs during depression in this preparation (Mennerick and Zorumski, 1995; Brody and Yue, 2000). Miniature EPSC amplitudes are representative of postsynaptic contributions, such as availability of neurotransmitter receptors and dendritic filtering properties. However, if the efficacy of synaptic transmission were reduced at presynaptic steps that occur before vesicle release, release-independent depression would result. Candidates include alterations in presynaptic action potentials (Hawkins et al., 1983), inactivation of presynaptic calcium channels (Patil et al., 1998), and desensitization of the release machinery to calcium (Hsu et al., 1996). Here we focused on presynaptic action potentials; calcium channel inactivation and release machinery desensitization will be the objects of future study.
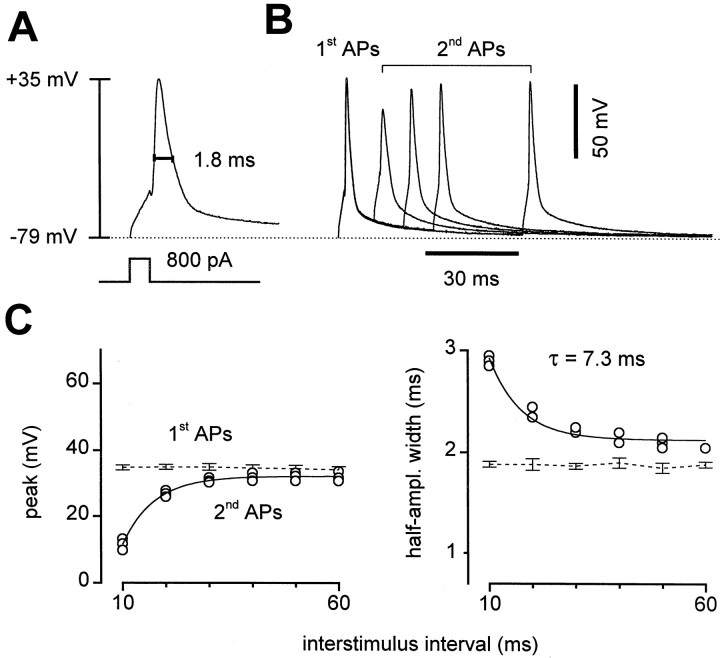
Somatic APs were recorded in current-clamp mode (see Materials and Methods) to generate hypotheses about the presynaptic APs (Fig.6). Single APs in control solutions plus NBQX peaked at 33.7 ± 2.5 mV (n = 12 cells) and were 1.47 ± 0.08 msec wide at half amplitude (Fig.6A). With short interstimulus intervals, the second APs were broader but considerably lower in amplitude. When the interstimulus interval was varied, the second APs regained amplitude with a time constant of 8.2 ± 2.3 msec (n = 5) (Fig. 6B,C), similar to the fast time constant of recovery from STD (Fig. 2). Even with 60 msec intervals, the second AP amplitudes did not fully return to the size of the first spike but reached a plateau 3.1 ± 1.0 mV lower. This too was similar to the recovery from STD in these cells, which also had an apparent plateau attributable to the slow component of recovery (Fig. 2). The widths of the second action potentials relaxed similarly with varying interstimulus intervals; both the amplitude and width curves could be fit by single exponentials with the same time constant (Fig. 6C). The spikes recovered entirely within 15 sec, but we were not able to resolve the time course of the slower phase of recovery. Thus we hypothesized that if the presynaptic action potentials were similar to those recorded at the somata, changes in their amplitude could be responsible for some or all of the STD.
Fig. 6.
Somatic APs. A, In current-clamp mode, current injection at the soma triggered brief APs. Measurement of peak (+35 mV) and half-amplitude width (1.8 msec) is illustrated.B, Four overlaid pairs of APs at varied interstimulus intervals. With pairs of current injections, peak amplitudes were lower and half-amplitude widths were greater for the second AP. C, The peak (left) and half-amplitude width (right) of the second AP recovered toward the values of the first AP with increasing interstimulus intervals. Recovery time courses for both parameters were well fit by single exponentials (solid lines) with the same time constant, 7.3 msec. Data from same cell as in A and B.
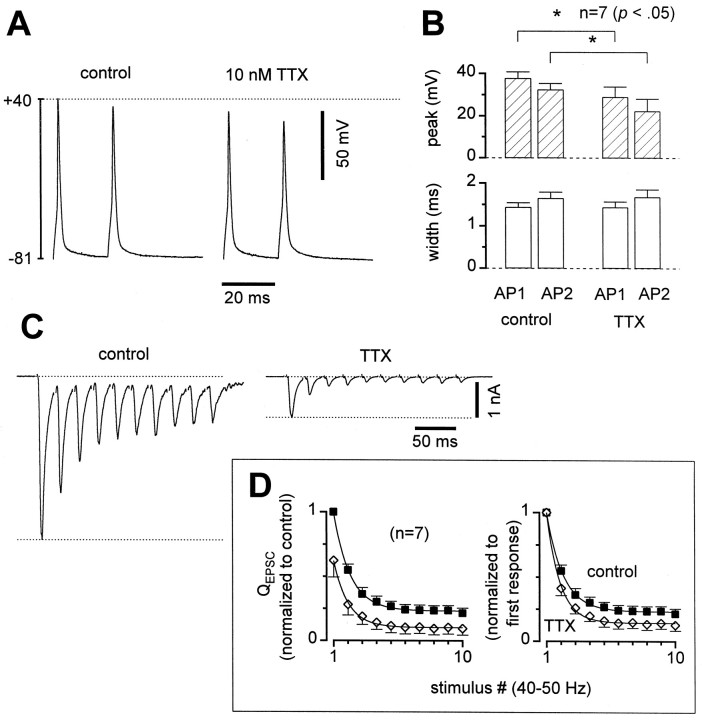
To support this hypothesis, we demonstrated that the EPSC sizes were sensitive to a manipulation that changed somatic AP amplitudes (Fig.7). Low doses of tetrodotoxin (TTX), a specific blocker of voltage-gated sodium channels, reduced somatic AP peak height while leaving half-amplitude widths unchanged (Fig.7A,B). A second spike triggered 20 msec later was also reduced in amplitude by a similar proportion, so that the ratio of second peak height to first peak height was not changed significantly in TTX (Fig.7A,B). Synaptic efficacy, as reflected in the EPSC sizes (back in voltage-clamp mode), decreased considerably in TTX (Fig. 7C) with an average reduction of ∼40% (Fig. 7D). Thus transmitter release was indeed sensitive to changes in the action potential amplitude. Furthermore, TTX increased depression (Fig. 7C,D), such that EPSCs were on average ∼10% of their initial amplitudes after 10 pulses, whereas they were ∼20% of initial size in control for this group of cells (Fig. 7D). The increase in depression in TTX provided further evidence that a presynaptic mechanism involving changes in the AP waveform produced the observed depression.
Fig. 7.
Low doses of TTX reduced AP and EPSC amplitudes, while increasing STD. A, Two pairs of current-clamped APs from the same cell, one in control and the other in 10 nmTTX, illustrating reduction in AP peak amplitudes. B, AP parameters averaged across cells. APs peaked lower and widths were unchanged in TTX. C, Sample EPSCs from a cell with larger-than-average effects of TTX. EPSCs were reduced 79%, and paired-pulse depression was increased from 31 to 62% in this cell.D, Normalized _Q_EPSC averages in control (solid squares) and TTX (open diamonds).Left, Normalized by the first EPSC in control. First EPSCs reduced 38 ± 13% in TTX. Right, Normalized by the first EPSC in each condition, to show increase in STD. Averages across seven cells, p values 0.02–0.12 for stimuli 2–10.
Three lines of experiments were performed to attempt to reduce short-term depression by strengthening presynaptic action potentials. First, lowering intracellular sodium to 4 mm decreased the extent of short-term depression: paired-pulse modulation, as gauged by the first two responses in a 50 Hz train, was 0.73 ± 0.03 (n = 4 cells; data not shown), whereas the paired-pulse modulation in control (12 mm Na+) was 0.57 ± 0.04, (data shown in Fig. 3). Depression was similarly affected during the remainder of the responses in 50 Hz trains. The differences in the extent of depression were statistically significant (p < 0.05) for each of the responses in the trains. This finding adds further to the evidence favoring action potential changes as a contributor to depression. In 4 mm[Na+]i, the remaining depression was still release independent, in that decreasing release probability with Cd2+ did not affect the extent of depression in three of the four cells.
Second, changing the membrane potential at the soma in the interstimulus intervals from −80 mV to −100 mV would be expected to substantially accelerate the recovery from inactivation of sodium channels (Kuo and Bean, 1994). However, hyperpolarization had no effect on depression (n = 8; data not shown). A negative result is inconclusive, however, because the relevant axonal sodium channels may be electrically too distant from the soma to be affected by changes in holding potential.
Finally, we applied the anemone toxin ATX II, which reduces sodium channel inactivation (Mantegazza et al., 1998) but had inconsistent effects on short-term plasticity (data not shown). Although other toxins might yield better results, we did not pursue this line of investigation further.
Evidence for action potential conduction failure
The somatic action potential results (Fig. 6), the effects of TTX (Fig. 7), and the findings with lowered [Na+]i pointed to a mechanism of depression involving decrements in the strength of axonal action potentials. This could occur in at least two ways. First, lower amplitude action potentials arriving at the presynaptic terminal could be less effective at opening the voltage-gated calcium channels that trigger vesicle release. Such changes would be expected to progressively decrease vesicle release probability (PR) in a release-independent manner. Alternatively, lower amplitude action potentials might be less likely to propagate through regions of high electrical impedance, such as through axonal branch points. If the probability of successful action potential conduction at axonal branches (PC) decreases with repetitive stimulation, net synaptic efficacy would be reduced, also in a release-independent manner. For the simplest formulation in which all branches and release sites are assumed to be identical and independent, these two alternatives would have indistinguishable effects on mean EPSC amplitudes. This is because the mean EPSC amplitudes are directly proportional to both PR and PC, as shown in Equation 1:
| 〈EPSC〉=NB PC SB PR q, | Equation 1 |
|---|
where NB represents the number of branches, SB is the number of release sites per branch, and q is the quantal EPSC size for each successful release.
Therefore, to distinguish between reduction in release probability versus increases in conduction failures at axonal branches, we calculated the expected EPSC variances for the two scenarios (Figs.8, 9;). Two experimental constraints were imposed on these calculations. First, the initial action potential conduction probability was taken to be close to 1 for all branches (Luscher et al., 1994b; Mackenzie et al., 1996; Mackenzie and Murphy, 1998). Second, the initial vesicle release probability was required to be less than 1/3.47 ≈ .29, because in an extracellular solution designed to maximize presynaptic calcium entry, including 4 mmCa2+ plus 100 μm 4-AP, the initial EPSCs were on average 3.47-fold larger than in control solutions (Fig.9A) (Brody and Yue, 2000). With these assumptions and constraints, the expected variances for the release probability model and the conduction failure model were distinct for a wide range of parameters (Fig. 8, ). Modeling depression attributable only to changes in release probability (PR) showed that the variance would decline monotonically with depression of mean EPSCs (Fig. 8A,D). Mean EPSCs in this case decreased in direct proportion to PR, and experimentally determined EPSC means and variances during a train of stimuli would map onto this relation at discrete points. When the assumption of identical release sites was relaxed, reduction in release probabilities produced similar monotonic declines in variance (data not shown). By contrast, in models of progressive decreases in action potential conduction probability (PC) alone, the expected variance could take a nonmonotonic course, rising and falling parabolically with decreasing mean EPSCs (Fig.8B,E). In this case, mean EPSCs decreased in direct proportion to PC, and the exact form of the mean–variance relation for such axonal branch point failure is given by Equation 2, as derived in the Appendix:
| ς2=NB PC PR SB q2[1−PC PR SB+PR (SB−1)]. | Equation 2 |
|---|
The extent of the rise and fall in variance increased with the number of release sites per axonal branch (_S_B) (Fig. 8B) and also depended on the release probability (see ). The sharper increases in peak variance for large values of SB occur because multiple release sites fail with conduction block of each axonal branch, creating stochastic “events” that are larger in amplitude than the release of individual vesicles. This feature is represented diagrammatically in Figure 8E. For a single release site for each branch (SB = 1), the two models were formally identical, because the equation reduced to the well known binomial variance formula (see ) (del Castillo and Katz, 1954; Faber and Korn, 1991). Thus, with sufficiently large numbers of release sites per branch, variance analysis could distinguish between depression arising from decreases in release probability and depression attributable to decreases in conduction probability.
For our analytic model of short-term depression caused by axonal branch point failure, we assumed that all axonal branches had the same number of sites (i.e., SB was constant) and the same probability of failing during depression (i.e., PC decreased uniformly at all branches). These assumptions were necessary for the derivation of an analytical relation between mean and variance (see ). When we relaxed these assumptions and numerically computed the expected variance for several possible nonuniform distributions of numbers of sites per branch (SB) and rate of decline in action potential conduction probability (PC) (see Materials and Methods), we found that the trends illustrated by our analytic result were maintained; depression attributable to branch point failure led under many circumstances to near-parabolic relations between mean and variance (Fig. 8C). This sort of heterogeneity in the numbers of sites per branch and action potential conduction probability is represented in the diagram in Figure 8F. Interestingly, as the dispersion in the number of sites per branch increased, the rise and fall in variance with progressive conduction failure became more extreme (Fig. 8C). This may occur because of the nonlinear relationship between the number of sites per branch and the magnitude of the peak in variance (see , Eq.EA11). Thus, the distinction in expected variance between depression arising from decreases in release probability and depression attributable to decreases in conduction probability did not depend critically on the simplifying assumptions used for the analytic solutions.
Experimentally, we observed a clear rise and fall in variance on average during short-term depression (Fig. 9). To ensure that rundown or patch instability did not contaminate variance estimates, cells were accepted for this analysis only if there were at least 10 continuous sweeps in control conditions with no systematic change in EPSC amplitudes over time (Fig. 9A). Also, EPSCs had to be at least twofold larger in 4 mm Ca2+ plus 100 μm 4-AP (Fig. 9A). This final requirement was met in all cells tested and was included to ensure that any nonmonotonic mean–variance relationships could not be caused by decreasing release probability (Silver et al., 1998). In total, seven cells met both of our criteria. In four of these, EPSC variances increased and then decreased with progressive depression of the mean (e.g., Fig. 9B, left). The mean–variance relations in these cells were well described by Equation 2 with relatively large values of SB. In the other three cells, there was not a resolvable rise in variance (e.g., Fig.9B, right), and the data were well described by Equation 2 with values of SB that were below the threshold for producing a distinct peak in variance (see , Eq.EA10, and Fig. 8B). Even in these cases, the data were better fit by the branch point failure equation (Fig. 9B,right, solid line) than by the binomial variance formula (dotted line), although this is not surprising, because the branch point failure equation has more free parameters than the binomial variance formula. Overall, the average across the seven cells showed a clear rise and fall in variance (Fig. 9C), which again was well fit by Equation 2 (Fig. 9C, solid curve). More complex models incorporating mixtures of types of depression provided still better fits (data not shown) but required additional free parameters. In the best fitting mixture models, conduction failure always contributed a substantial part to the overall depression (data not shown). Thus, the experimental measurements of EPSC variance were consistent with action potential conduction failure underlying the short-term depression.
It is worth noting that interpretation of the variance data requires an assumption about the initial action potential conduction probabilities and vesicle release probabilities (see ). In particular, we interpret the rise and fall of variance to mean that the probability of action potential conduction (PC) started close to 1 and declined with short-term depression; the maximal variance occurred for intermediate values of PC (see). Alternatively, however, this parabolic variance could have been caused by vesicle release probabilities (PR) initially near 1 that declined during depression (Silver et al., 1998). This alternative scenario could be consistent with our data if we interpreted the more than twofold increase in EPSCs with 4 mm Ca2+ plus 4-AP as evidence that PC was initially <0.5. Indeed, it has been reported in abstract form that conduction failures during single stimuli may be responsible for some “silent synapses” in cultured neurons (Thio and Yamada, 1998). However, the balance of the published data in the literature supports the assumption that the release probabilities were initially low and that action potential conduction was initially reliable (Hessler et al., 1993; Allen and Stevens, 1994; Luscher et al., 1994b; Mackenzie et al., 1996; Mackenzie and Murphy, 1998). Thus the most likely explanation of the variance data is that conduction failures were responsible for the depression.
DISCUSSION
We have found that in hippocampal neurons grown in microisland cultures, short-term synaptic depression had several unusual features. The depression was not caused by a release-dependent mechanism such as vesicle depletion, because depression was unaffected by reduction of initial release probability with Cd2+. This was confirmed by the absence of an inverse correlation between successive, relative EPSC sizes that would be expected for release-dependent depression. Instead, one source of STD could be progressive increases in the probability of AP conduction failure along axonal branches. Four lines of evidence favored this mechanism. The somatic AP amplitudes declined with repetitive stimulation, modest reduction in AP amplitude with tetrodotoxin inhibited EPSCs significantly, lowering of [Na+]i decreased depression, and the variance of EPSCs rose and fell with monotonic depression of the EPSC mean.
Can the observed changes in APs account entirely for the depression in EPSCs? There are several factors that preclude a definitive answer. First, somatic APs may be different from those at branch points and terminals, because of differences in the geometry, membrane properties, and/or distribution of ionic channels at various subcellular locations (Hoffman et al., 1997). Second, there are nonlinearities in the relations between spike amplitudes and conduction through axonal branch points, plus complex effects of AP parameters on synaptic release probability.
Recent experimental findings and detailed simulations (Streit et al., 1992; Luscher et al., 1994a,b; Debanne et al., 1997; Kopysova and Debanne, 1998) make conduction failure seem a reasonable possibility. However, we have not directly observed this AP conduction failure, so other mechanisms not explicitly excluded are possible. We also cannot say whether conduction failure entirely explains depression; there could be other release-independent depression mechanisms acting concurrently. Candidates for such mechanisms include desensitization of synaptic release machinery (Hsu et al., 1996), reduction of calcium entry attributable to lower amplitude APs arriving at the presynaptic terminal (Hawkins et al., 1983), and presynaptic calcium channel inactivation (Patil et al., 1998). Regardless of the exact quantitative contributions of action potential conduction failures versus other mechanisms, an important conclusion was that depression was entirely release independent; there was no resolvable component of release-dependent depression (Figs. 3-5).
The presence of release-independent depression was unexpected, because reducing release probability by changing extracellular Ca2+ and/or Mg2+ concentrations (ΔCa/Mg) reduced depression in a previous report (Mennerick and Zorumski, 1995) and in a subset of our experiments. We investigated this seeming contradiction and found that the effects of ΔCa/Mg on depression did not correlate with the extent of inhibition. Instead, they appeared inversely related to the strength of the baseline depression; the smallest effects of ΔCa/Mg occurred in cells with the strongest depression. Thus, this result also does not support a release-dependent depression mechanism. In other preparations, supplemental findings have been used to confirm the presence of release-dependent depression. For example, in hippocampal slice cultures there was indeed an inverse correlation between successive relative EPSC sizes, as expected for a release-dependent mechanism (Debanne et al., 1996). Also, in the chick nucleus magnocellularis, lowering Ca2+ and adding Cd2+both reduced depression significantly, although not identically (Otis and Trussell, 1996). However, in our hands, the results of the same sorts of experiments pointed toward a release-independent mechanism in cultured hippocampal neurons. Thus, one important conclusion is that decreased depression in ΔCa/Mg is not necessarily indicative by itself of release-dependent STD.
We can only speculate about why these surprising effects of ΔCa/Mg might have occurred, in light of the action potential conduction failure hypothesis. As noted above, lowering Ca2+concentrations may reduce membrane surface charge screening (Frankenhaeuser and Hodgkin, 1957), making voltage-gated ion channels more readily activated and action potential propagation more reliable. Raising Mg2+ does not entirely compensate for this (Rahamimoff, 1968; Kostyuk et al., 1982; Wilson et al., 1983), because local surface charges may be channel specific (Green and Andersen, 1991) and there may be additional screening effects caused by calcium-selective binding sites (Krafte and Kass, 1988). Indeed, in some cells, the second somatic action potential was more similar to the first in 1 Ca/2 Mg than in control solutions (data not shown). However, we were unable to demonstrate this effect reliably and cannot say whether it occurs in the axonal branches. Another possibility is that ΔCa/Mg may affect action potential conduction reliability via changes in the submicroscopic calcium domains near open calcium channels. Reducing unitary calcium currents by changing the permeant ion concentrations (Church and Stanley, 1996) would be expected to have a different effect on these domains than lowering calcium channel open probability with Cd2+ (Lansman et al., 1986; Bertram et al., 1999). Such domains have been shown to be responsible for triggering various calcium-dependent processes, including L-type calcium channel inactivation (Imredy and Yue, 1992), calcium-activated potassium channel gating (Roberts et al., 1990), and transmitter release itself (Llinas et al., 1992). Interestingly, reduction in extracellular calcium was observed to make action potential conduction more reliable in cultured dorsal root ganglion cells (Luscher et al., 1994b) and motoneurons cocultured with skeletal muscle (Streit et al., 1992). Hot spots of calcium elevation have been visualized at branch points (Llano et al., 1997; Koizumi et al., 1999) where they may be involved in the regulation of axonal excitability.
It will be important to determine whether these potential mechanisms can account for the differences between the effects of ΔCa/Mg and Cd2+ and for the correlation observed between initial depression and the effects of ΔCa/Mg (Fig.4D). This correlation (Fig. 4D) may reflect more robust action potential conduction failure in the cells with the greatest baseline depression. If changes in [Ca2+]o or [Mg2+]o modestly enhance membrane excitability, then in cells with axonal branch points that are farther from the threshold for successful AP conduction, such enhancements may be insufficient to bring the membrane potential at the branch point above the threshold for action potential propagation. In contrast, cells with axonal branch points that are closer to conduction thresholds might have less overall branch point failure, and enhancements in excitability could be more effective at elevating the probability of successful conduction.
On the subject of axonal conduction failure, this mechanism has been shown previously to produce frequency-dependent synaptic depression in several invertebrate and mammalian preparations (Parnas, 1972; Hatt and Smith, 1976; Smith, 1983; Streit et al., 1992) and has been reported in other contexts as well. Hyperpolarization-induced recovery from inactivation of voltage-gated potassium channels caused conduction failures at a subset of axonal branches in hippocampal slices (Debanne et al., 1997). Such conduction failures also play a role in spinal cord axons (Barron and Matthews, 1935), leech sensory axons (Macagno et al., 1987; Gu, 1991), rat neurohypophysis (Dyball et al., 1988), dorsal root ganglion neurons (Luscher et al., 1994a,b, 1996), and mammalian lower motor neuron arborizations (Wall and McMahon, 1994; Wall, 1995).
Direct observations of AP conduction failure in our preparation will be important. Optical imaging of the entire course of an axon using voltage-sensitive dyes (Larkum et al., 1996) would reveal the sites of action potential failures, the number of presynaptic terminals affected by failures, and the relationship between axonal geometry and AP amplitudes. Such experiments would allow investigation of whether inactivation of both Na+ and K+conductances contribute to frequency-dependent changes in the relevant action potential waveforms. Inactivation of both channel types seems to be involved, as isolated reduction in Na+ current density using TTX partially, but not entirely, reproduced the effects of repetitive stimulation on spike waveforms (Figs. 6, 7).
Alternatively, optically imaged presynaptic calcium transients at individual terminals have been used as surrogate markers for AP arrival (Mackenzie et al., 1996; Mackenzie and Murphy, 1998). If all terminals arising from one axonal branch concurrently failed to show calcium entry, it would be strong evidence for conduction failure. Such experiments seem feasible in dispersed neuronal cultures (Larkum et al., 1996; Mackenzie et al., 1996; Mackenzie and Murphy, 1998).
Although cultured neurons can be significantly different from those_in vivo_ (Banker and Cowan, 1979), AP conduction failure could be relevant to more intact preparations. For example, hippocampal AP bursts in vivo have amplitudes that decrement during the burst (Fox and Ranck, 1975; Ishizuka et al., 1990), possibly making later APs propagate less reliably through axonal branches. Both hippocampal and neocortical axons have numerous branches, with multiple varicosities (presumed to be synaptic contacts) per axonal branch (Harris and Woolsey, 1983; Ishizuka et al., 1990; Li et al., 1994). Thus the consequences of AP conduction failure would be distinct from failure to release transmitter at individual release sites. Interestingly, release-independent depression has been noted in hippocampal slices (Dobrunz et al., 1997). By using the pharmacological and analytical techniques developed here, in addition to multi-electrode recordings (Debanne et al., 1997), the conduction failure hypothesis could be tested in preparations that more closely represent the in vivo workings of the nervous system. Further theoretical work may be required to elucidate the effect of this mechanism on neuronal information transfer.
In this Appendix, we have derived a formula for the variance of the EPSCs during STD caused by action potential conduction failures at axonal branches. For simplicity, we assumed that all axonal branches, synaptic release sites, and quantal sizes were equal and independent.
Suppose a presynaptic neuron has an axon that divides into NB identical branches. Let action potentials conduct through each branch with probability PC. We modeled synaptic depression attributable to propagation failures as progressive decreases in this parameter PC. Furthermore, suppose there are SB identical synaptic release sites per branch, each of which has a probability PR of releasing a vesicle given that an action potential conducted through its branch. Without conduction into a branch, release sites distal to the branch have negligible probability of release. All successful release events were assumed to contribute an EPSC of size q, and individual EPSCs were assumed to sum linearly. Thus the expected value of the total EPSC size in this situation can be thought of as proportional to the number of branches that successfully conduct times the number of successful releases at each conducting branch:
| 〈EPSC〉=NB PC SB PR q. | Equation A1 |
|---|
The probability that any particular size EPSC occurred was calculated as a summation, incorporating all of the different ways in which the result could occur:
=∑b=1NB P(EPSC=nq‖b branches conduct)
| =∑b=1NB PRn(1−PR)b SB−nb SBnPCb(1−PC)NB−bNBb, | Equation A2 |
|---|
wherexy=x!y!(x−y)!.
We next used Equation EA2 to find the second moment of the EPSCs, 〈EPSC2〉, and then calculated the variance from the second moment and from Equation EA1, using ς2 = 〈EPSC2〉 − 〈EPSC〉2:
〈EPSC2〉=∑n=1NB SB P(EPSC=nq)(nq)2.
Therefore:
| 〈EPSC2〉=∑n=1NB SB ∑b=1NB PRn(1−PR)b SB−nbSBnPCb(1−PC)NB−b | Equation A3 |
|---|
PCb(1−PC)NB−bNBbwas brought out of the sum over n in Equation EA3 because it does not depend on n, yielding:
〈EPSC2〉=∑b=1NBPCb(1−PC)NB−bNBb∑n=1NB SB PRn(1−PR)b SB−n
The upper limit was then changed from NB SB to bSB in the sum over n becausebSBn=0for n > bSB, giving:
| 〈EPSC2〉=∑b=1NBPCb(1−PC)NB−bNBb∑n=1bSB PRn(1−PR)bSB−n | Equation A4 |
|---|
Equation EA4 was simplified in two steps. First, we recognized that∑b SBn=1 PRn(1−PR)b SB−nbSBn(nq)2was the second moment of the sum of bSB binomial variables, each with success probability PR and amplitude q. Because the sum of bSBsuch binomial variables has variance b SB PR(1 − PR) q2 and mean b SB PR q, this second moment equaled b SB PR(1 − PR) q2 + (b SB PR q)2. Substituting into Equation EA4 yielded:
〈EPSC2〉=∑b=1NB(PC)b(1−PC)NB−bNBb[bSB PR(1−PR)q2
ς2=∑b=1NB(PC)b(1−PC)NB−bNBb[bSB PR(1−PR)q2
| +(bSB PR q)2]−(NB PC SB PR q)2. | Equation A5 |
|---|
For the second simplification, we used the assumptions that the total EPSC was the sum of the contributions from each of the individual branches and that the branches were independent. Because the variance of a sum of identical, independent variables is just the number of variables times the variance of each, the total variance was equal to NB times the variance determined for NB = 1:
| ς(1)2=PC[SB PR(1−PR)q2+(SB PR q)2]−(PC SB PR q)2 | Equation A6 |
|---|
| ς(NB)2=NB {PC [SB PR(1−PR)q2+(SB PR q)2]−(PC SB PR q)2} | Equation A7 |
|---|
=NB PC PR SB q2[1−PC PR SB+PR(SB−1)].
Equation EA7 was reproduced as Equation 2 in Results. For SB = 1, Equation EA7 reduced to the well known binomial variance formula NP(1 − P)q2 with N = NBand P = PC PR. It similarly reduced to the binomial formula if PC = 1, in this case with N = NB SB and P = PR.
We next calculated the value of PC at which the maximal variance occurred, termed PC,Peak. The derivative of Equation EA7 with respect to PCwas:
| ∂ς(NB)2∂PC=NB PR SB q2[1−PC PR SB+PR(SB−1)]−NB PC (PR SB)2q2, | Equation A8 |
|---|
and setting∂ς(NB)2∂PC=0yielded:
| PC,Peak=1+PRSB−PR2PRSB. | Equation A9 |
|---|
Because∂2ς(NB)2∂PC2=−2NB(PRSB)2q2<0,the extremum in variance at PC,Peak was a maximum.
It was important to determine whether this peak in variance could actually be seen in a physiological situation by demonstrating that 0 ≤ PC,Peak ≤ 1 and that the relative increase in variance,ς2(PC=PC,Peak)ς2(PC=1),would not be negligibly close to 1 under reasonable conditions.
We first derived the conditions required for PC,Peak ≤ χ. The more general constraint PC,Peak ≤ χ was used instead of PC,Peak ≤ 1 because we might not be able to experimentally resolve peaks that occur for PC,Peak very close to 1, and therefore might choosefor instance χ = 0.8. The constraint PC,Peak ≤ χ was satisfied when either of two equivalent conditions was met:
| PR≥11+(2χ−1)SB⇔SB≥1−PRPR(2χ−1). | Equation A10 |
|---|
This constraint was satisfied for many realistic sets of parameters. For example, with χ = 0.8 and PR = 0.1, SB would have to be ≥15 to see a distinct peak in variance. Note that if the constraint were not satisfied and there was not a distinct peak in variance, Equation EA7 still could be useful to quantitatively describe the variance when action potential propagation failure at axonal branches may be responsible for the observed STD (e.g., Fig.9B, right).
Second, we wanted to see what order of magnitude we could expect from a potential rise in variance:
ς(NB)2(PC=PC,Peak)ς(NB)2(PC=1)
=NB PC,Peak PR SB q2[1−PC,Peak PR SB+PR(SB−1)]NB PR SB q2[1−PR SB+PR(SB−1)]
| =(1+PR SB−PR)24PR SB(1−PR). | Equation A11 |
|---|
This ratio could be substantial for appropriate values of PR and SB, and the value of Equation EA11 always increased with SB as long asSB≥1−PRPR(e.g., Fig. 8B). Thus, the qualitative and quantitative properties of the expected EPSC variance during short-term depression attributable to action potential conduction failures could be described in a simple, analytical manner.
Footnotes
This work was supported by National Institutes of Health (NIH) (R01) and National Science Foundation (PFF) grants to D. T. Y. and an NIH Medical Scientist Training Program fellowship to D. L. B.
We thank C. Boyer and C. F. Stevens for the microisland culture protocol, A. Ghosh, C. Jahr, and C. Zorumski for initial advice on neuronal cell culture, and C. Aizenmann, H. Colecraft, D. DiGregorio, J. Dittmann, L. Jones, D. Linden, and P. Fuchs for helpful discussions and comments on this manuscript.
Correspondence should be addressed to David T. Yue, The Johns Hopkins University School of Medicine, Departments of Biomedical Engineering and Neuroscience, Program in Molecular and Cellular Systems Physiology, 720 Rutland Avenue, Baltimore, MD 21205. E-mail: dyue@bme.jhu.edu.
REFERENCES
- 1.Abbott LF, Varela JA, Sen K, Nelson SB. Synaptic depression and cortical gain control. Science. 1997;275:220–224. doi: 10.1126/science.275.5297.221. [DOI] [PubMed] [Google Scholar]
- 2.Alger BE, Teyler TJ. Long-term and short-term plasticity in the CA1, CA3, and dentate regions of the rat hippocampal slice. Brain Res. 1976;110:463–480. doi: 10.1016/0006-8993(76)90858-1. [DOI] [PubMed] [Google Scholar]
- 3.Allen C, Stevens CF. An evaluation of causes for unreliability of synaptic transmission. Proc Natl Acad Sci USA. 1994;91:10380–10383. doi: 10.1073/pnas.91.22.10380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Banker GA, Cowan WM. Further observations on hippocampal neurons in dispersed cell culture. J Comp Neurol. 1979;187:469–493. doi: 10.1002/cne.901870302. [DOI] [PubMed] [Google Scholar]
- 5.Barron DH, Matthews B. Intermittent conduction in the spinal cord. J Physiol (Lond) 1935;85:73–103. doi: 10.1113/jphysiol.1935.sp003303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bekkers JM, Stevens CF. Excitatory and inhibitory autaptic currents in isolated hippocampal neurons maintained in cell culture. Proc Natl Acad Sci USA. 1991;88:7834–7838. doi: 10.1073/pnas.88.17.7834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bertram R, Smith GD, Sherman A. Modeling study of the effects of overlapping Ca2+ microdomains on neurotransmitter release. Biophys J. 1999;76:735–750. doi: 10.1016/S0006-3495(99)77240-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brody DL, Yue DT. Relief of G-protein inhibition of calcium channels and short-term synaptic facilitation in cultured hippocampal neurons. J Neurosci. 2000;20:889–898. doi: 10.1523/JNEUROSCI.20-03-00889.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Church PJ, Stanley EF. Single L-type calcium channel conductance with physiological levels of calcium in chick ciliary ganglion neurons. J Physiol (Lond) 1996;496:59–68. doi: 10.1113/jphysiol.1996.sp021665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Debanne D, Guerineau NC, Gahwiler BH, Thompson SM. Paired-pulse facilitation and depression at unitary synapses in rat hippocampus: quantal fluctuation affects subsequent release. J Physiol (Lond) 1996;491:163–176. doi: 10.1113/jphysiol.1996.sp021204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Debanne D, Guerineau NC, Gahwiler BH, Thompson SM. Action-potential propagation gated by an axonal I(A)-like K+ conductance in hippocampus. Nature. 1997;389:286–289. doi: 10.1038/38502. [DOI] [PubMed] [Google Scholar]
- 12.del Castillo J, Katz B. Quantal components of the end-plate potential. J Physiol (Lond) 1954;124:560–573. doi: 10.1113/jphysiol.1954.sp005129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Deuchars J, Thomson AM. CA1 pyramid-pyramid connections in rat hippocampus in vitro: dual intracellular recordings with biocytin filling. Neuroscience. 1996;74:1009–1018. doi: 10.1016/0306-4522(96)00251-5. [DOI] [PubMed] [Google Scholar]
- 14.Dobrunz LE, Stevens CF. Heterogeneity of release probability, facilitation, and depletion at central synapses. Neuron. 1997;18:995–1008. doi: 10.1016/s0896-6273(00)80338-4. [DOI] [PubMed] [Google Scholar]
- 15.Dobrunz LE, Huang EP, Stevens CF. Very short-term plasticity in hippocampal synapses. Proc Natl Acad Sci USA. 1997;94:14843–14847. doi: 10.1073/pnas.94.26.14843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dyball RE, Grossmann R, Leng G, Shibuki K. Spike propagation and conduction failure in the rat neural lobe. J Physiol (Lond) 1988;401:241–256. doi: 10.1113/jphysiol.1988.sp017160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Faber DS, Korn H. Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys J. 1991;60:1288–1294. doi: 10.1016/S0006-3495(91)82162-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fox SE, Ranck JB., Jr Localization and anatomical identification of theta and complex spike cells in dorsal hippocampal formation of rats. Exp Neurol. 1975;49:299–313. doi: 10.1016/0014-4886(75)90213-7. [DOI] [PubMed] [Google Scholar]
- 19.Frankenhaeuser B, Hodgkin AL. The action of calcium on the electrical properties of squid axons. J Physiol (Lond) 1957;137:218–244. doi: 10.1113/jphysiol.1957.sp005808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Furshpan EJ, Landis SC, Matsumoto SG, Potter DD. Synaptic functions in rat sympathetic neurons in microcultures. I. Secretion of norepinephrine and acetylcholine. J Neurosci. 1986;6:1061–1079. doi: 10.1523/JNEUROSCI.06-04-01061.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Green WN, Andersen OS. Surface charges and ion channel function. Annu Rev Physiol. 1991;53:341–359. doi: 10.1146/annurev.ph.53.030191.002013. [DOI] [PubMed] [Google Scholar]
- 22.Gu XN. Effect of conduction block at axon bifurcations on synaptic transmission to different postsynaptic neurones in the leech. J Physiol (Lond) 1991;441:755–778. doi: 10.1113/jphysiol.1991.sp018777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hanck DA, Sheets MF. Extracellular divalent and trivalent cation effects on sodium current kinetics in single canine cardiac purkinje cells. J Physiol (Lond) 1992;454:267–298. doi: 10.1113/jphysiol.1992.sp019264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harris RM, Woolsey TA. Computer-assisted analyses of barrel neuron axons and their putative synaptic contacts. J Comp Neurol. 1983;220:63–79. doi: 10.1002/cne.902200107. [DOI] [PubMed] [Google Scholar]
- 25.Hatt H, Smith DO. Synaptic depression related to presynaptic axon conduction block. J Physiol (Lond) 1976;259:367–393. doi: 10.1113/jphysiol.1976.sp011471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hawkins RD, Abrams TW, Carew TJ, Kandel ER. A cellular mechanism of classical conditioning in Aplysia: activity-dependent amplification of presynaptic facilitation. Science. 1983;219:400–405. doi: 10.1126/science.6294833. [DOI] [PubMed] [Google Scholar]
- 27.Hessler NA, Shirke AM, Malinow R. The probability of transmitter release at a mammalian central synapse. Nature. 1993;366:569–572. doi: 10.1038/366569a0. [DOI] [PubMed] [Google Scholar]
- 28.Hoffman DA, Magee JC, Colbert CM, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387:869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- 29.Hsu SF, Augustine GJ, Jackson MB. Adaptation of Ca2+-triggered exocytosis in presynaptic terminals. Neuron. 1996;17:501–512. doi: 10.1016/s0896-6273(00)80182-8. [DOI] [PubMed] [Google Scholar]
- 30.Imredy JP, Yue DT. Submicroscopic Ca2+ diffusion mediates inhibitory coupling between individual Ca2+ channels. Neuron. 1992;9:197–207. doi: 10.1016/0896-6273(92)90159-b. [DOI] [PubMed] [Google Scholar]
- 31.Ishizuka N, Weber J, Amaral DG. Organization of intrahippocampal projections originating from CA3 pyramidal cells in the rat. J Comp Neurol. 1990;295:580–623. doi: 10.1002/cne.902950407. [DOI] [PubMed] [Google Scholar]
- 32.Koizumi S, Bootman MD, Bobanovic LK, Schell MJ, Berridge MJ, Lipp P. Characterization of elementary Ca2+ release signals in NGF-differentiated PC12 cell and hippocampal neurons. Neuron. 1999;22:125–137. doi: 10.1016/s0896-6273(00)80684-4. [DOI] [PubMed] [Google Scholar]
- 33.Kopysova IL, Debanne D. Critical role of axonal A-type K+ channels and axonal geometry in the gating of action potential propagation along CA3 pyramidal cell axons: a simulation study. J Neurosci. 1998;18:7436–7451. doi: 10.1523/JNEUROSCI.18-18-07436.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kostyuk PG, Mironov SL, Doroshenko PA, Ponomarev VN. Surface charges on the outer side of mollusc neuron membrane. J Membr Biol. 1982;70:171–179. [Google Scholar]
- 35.Krafte DS, Kass RS. Hydrogen ion modulation of Ca2+ channel current in cardiac ventricular cells. Evidence for multiple mechanisms. J Gen Physiol. 1988;91:641–657. doi: 10.1085/jgp.91.5.641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kuo CC, Bean BP. Na+ channels must deactivate to recover from inactivation. Neuron. 1994;12:819–829. doi: 10.1016/0896-6273(94)90335-2. [DOI] [PubMed] [Google Scholar]
- 37.Kusano K, Landau EM. Depression and recovery of transmission at the squid giant synapse. J Physiol (Lond) 1975;245:13–22. doi: 10.1113/jphysiol.1975.sp010832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lansman JB, Hess P, Tsien RW. Blockade of current through single calcium channels by Cd2+, Mg2+, and Ca2+. Voltage and con-centration dependence of calcium entry into the pore. J Gen Physiol. 1986;88:321–347. doi: 10.1085/jgp.88.3.321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Larkum ME, Rioult MG, Luscher HR. Propagation of action potentials in the dendrites of neurons from rat spinal cord slice cultures. J Neurophysiol. 1996;75:154–170. doi: 10.1152/jn.1996.75.1.154. [DOI] [PubMed] [Google Scholar]
- 40.Leonard JP, Nargeot J, Snutch TP, Davidson N, Lester HA. Ca2+ channels induced in Xenopus oocytes by rat brain mRNA. J Neurosci. 1987;7:875–881. doi: 10.1523/JNEUROSCI.07-03-00875.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Li XG, Somogyi P, Ylinen A, Buzsaki G. The hippocampal CA3 network: an in vivo intracellular labeling study. J Comp Neurol. 1994;339:181–208. doi: 10.1002/cne.903390204. [DOI] [PubMed] [Google Scholar]
- 42.Llano I, Tan YP, Caputo C. Spatial heterogeneity of intracellular Ca2+ signals in axons of basket cells from rat cerebellar slices. J Physiol (Lond) 1997;502:509–519. doi: 10.1111/j.1469-7793.1997.509bj.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Llinas R, Sugimori M, Silver RB. Microdomains of high calcium concentration in a presynaptic terminal. Science. 1992;256:677–679. doi: 10.1126/science.1350109. [DOI] [PubMed] [Google Scholar]
- 44.Lomo T. Potentiation of monosynaptic EPSPs in the perforant path-dentate granule cell synapse. Exp Brain Res. 1971;12:46–63. [PubMed] [Google Scholar]
- 45.Luscher C, Streit J, Quadroni R, Luscher HR. Action potential propagation through embryonic dorsal root ganglion cells in culture. I. Influence of the cell morphology on propagation properties. J Neurophysiol. 1994a;72:622–633. doi: 10.1152/jn.1994.72.2.622. [DOI] [PubMed] [Google Scholar]
- 46.Luscher C, Streit J, Lipp P, Luscher HR. Action potential propagation through embryonic dorsal root ganglion cells in culture. II. Decrease of conduction reliability during repetitive stimulation. J Neurophysiol. 1994b;72:634–643. doi: 10.1152/jn.1994.72.2.634. [DOI] [PubMed] [Google Scholar]
- 47.Luscher C, Lipp P, Luscher HR, Niggli E. Control of action potential propagation by intracellular Ca2+ in cultured rat dorsal root ganglion cells. J Physiol (Lond) 1996;490:319–324. doi: 10.1113/jphysiol.1996.sp021146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Macagno ER, Muller KJ, Pitman RM. Conduction block silences parts of a chemical synapse in the leech central nervous system. J Physiol (Lond) 1987;387:649–664. doi: 10.1113/jphysiol.1987.sp016593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mackenzie PJ, Murphy TH. High safety factor for action potential conduction along axons but not dendrites of cultured hippocampal and cortical neurons. J Neurophysiol. 1998;80:2089–2101. doi: 10.1152/jn.1998.80.4.2089. [DOI] [PubMed] [Google Scholar]
- 50.Mackenzie PJ, Umemiya M, Murphy TH. Ca2+ imaging of CNS axons in culture indicates reliable coupling between single action potentials and distal functional release sites. Neuron. 1996;16:783–795. doi: 10.1016/s0896-6273(00)80098-7. [DOI] [PubMed] [Google Scholar]
- 51.Magleby KL. Short-term changes in synaptic efficacy. In: Edelman GM, Gall WE, Cowan WM, editors. Synaptic function. Wiley; New York: 1987. pp. 21–56. [Google Scholar]
- 52.Mantegazza M, Franceschetti S, Avanzini G. Anemone toxin (ATX II)-induced increase in persistent sodium current: effects on the firing properties of rat neocortical pyramidal neurones. J Physiol (Lond) 1998;507:105–116. doi: 10.1111/j.1469-7793.1998.105bu.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Markram H, Tsodyks M. Redistribution of synaptic efficacy between neocortical pyramidal neurons. Nature. 1996;382:807–810. doi: 10.1038/382807a0. [DOI] [PubMed] [Google Scholar]
- 54.Mennerick S, Zorumski CF. Paired-pulse modulation of fast excitatory synaptic currents in microcultures of rat hippocampal neurons. J Physiol (Lond) 1995;488:85–101. doi: 10.1113/jphysiol.1995.sp020948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Murthy VN, Sejnowski TJ, Stevens CF. Heterogeneous release properties of visualized individual hippocampal synapses. Neuron. 1997;18:599–612. doi: 10.1016/s0896-6273(00)80301-3. [DOI] [PubMed] [Google Scholar]
- 56.Otis TS, Trussell LO. Inhibition of transmitter release shortens the duration of the excitatory synaptic current at a calyceal synapse. J Neurophysiol. 1996;76:3584–3588. doi: 10.1152/jn.1996.76.5.3584. [DOI] [PubMed] [Google Scholar]
- 57.Parnas I. Differential block at high frequency of branches of a single axon innervating two muscles. J Neurophysiol. 1972;35:903–914. doi: 10.1152/jn.1972.35.6.903. [DOI] [PubMed] [Google Scholar]
- 58.Patil PG, Brody DL, Yue DT. Preferential closed-state inactivation of neuronal calcium channels. Neuron. 1998;20:1027–1038. doi: 10.1016/s0896-6273(00)80483-3. [DOI] [PubMed] [Google Scholar]
- 59.Rahamimoff R. A dual effect of calcium ions on neuromuscular facilitation. J Physiol (Lond) 1968;195:471–480. doi: 10.1113/jphysiol.1968.sp008468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Reyes A, Lujan R, Rozov A, Burnashev N, Somogyri P, Sakmann B. Target-cell-specific facilitation and depression in neocortical circuits. Nat Neurosci. 1998;1:279–285. doi: 10.1038/1092. [DOI] [PubMed] [Google Scholar]
- 61.Roberts WM, Jacobs RA, Hudspeth AJ. Colocalization of ion channels involved in frequency selectivity and synaptic transmission at presynaptic active zones of hair cells. J Neurosci. 1990;10:3664–3684. doi: 10.1523/JNEUROSCI.10-11-03664.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Silver RA, Momiyama A, Cull-Candy SG. Locus of frequency-dependent depression identified with multiple-probability fluctuation analysis at rat climbing fibre-Purkinje cell synapses. J Physiol (Lond) 1998;510:881–902. doi: 10.1111/j.1469-7793.1998.881bj.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Smith DO. Variable activation of synaptic release sites at the neuromuscular junction. Exp Neurol. 1983;80:520–528. doi: 10.1016/0014-4886(83)90304-7. [DOI] [PubMed] [Google Scholar]
- 64.Stevens CF, Tsujimoto T. Estimates for the pool size of releasable quanta at a single central synapse and for the time required to refill the pool. Proc Natl Acad Sci USA. 1995;92:846–849. doi: 10.1073/pnas.92.3.846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Streit J, Luscher C, Luscher HR. Depression of postsynaptic potentials by high-frequency stimulation in embryonic motoneurons grown in spinal cord slice cultures. J Neurophysiol. 1992;68:1793–1803. doi: 10.1152/jn.1992.68.5.1793. [DOI] [PubMed] [Google Scholar]
- 66.Thio LL, Yamada KA. Branch point failure causes silent autapses in cultured postnatal rat hippocampal neurons. Soc Neurosci Abstr. 1998;25:566. [Google Scholar]
- 67.Thomson AM. Activity-dependent properties of synaptic transmission at two classes of connections made by rat neocortical pyramidal axons in vitro. J Physiol (Lond) 1997;502:131–147. doi: 10.1111/j.1469-7793.1997.131bl.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Thomson AM, Deuchars J. Temporal and spatial properties of local circuits in neocortex. Trends Neurosci. 1994;17:119–126. doi: 10.1016/0166-2236(94)90121-x. [DOI] [PubMed] [Google Scholar]
- 69.Thomson AM, West DC. Fluctuations in pyramid-pyramid excitatory postsynaptic potentials modified by presynaptic firing pattern and postsynaptic membrane potential using paired intracellular recordings in rat neocortex. Neuroscience. 1993;54:329–346. doi: 10.1016/0306-4522(93)90256-f. [DOI] [PubMed] [Google Scholar]
- 70.Thomson AM, Deuchars J, West DC. Large, deep layer pyramid-pyramid single axon EPSPs in slices of rat motor cortex display paired pulse and frequency-dependent depression, mediated presynaptically and self-facilitation, mediated postsynaptically. J Neurophysiol. 1993;70:2354–2369. doi: 10.1152/jn.1993.70.6.2354. [DOI] [PubMed] [Google Scholar]
- 71.Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA. 1997;94:719–723. doi: 10.1073/pnas.94.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Van der Loos H, Glaser EM. Autapses in neocortex cerebri: synapses between a pyramidal cell's axon and its own dendrites. Brain Res. 1972;48:355–360. doi: 10.1016/0006-8993(72)90189-8. [DOI] [PubMed] [Google Scholar]
- 73.Varela JA, Sen K, Gibson J, Fost J, Abbott LF, Nelson SB. A quantitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J Neurosci. 1997;17:7926–7940. doi: 10.1523/JNEUROSCI.17-20-07926.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Wall PD. Do nerve impulses penetrate terminal arborizations? A pre-presynaptic control mechanism. Trends Neurosci. 1995;18:99–103. doi: 10.1016/0166-2236(95)93883-y. [DOI] [PubMed] [Google Scholar]
- 75.Wall PD, McMahon SB. Long range afferents in rat spinal cord. III. Failure of impulse transmission in axons and relief of the failure after rhizotomy of dorsal roots. Philos Trans R Soc Lond B Biol Sci. 1994;343:211–223. doi: 10.1098/rstb.1994.0022. [DOI] [PubMed] [Google Scholar]
- 76.Wilson DL, Morimoto K, Tsuda Y, Brown AM. Interaction between calcium ions and surface charge as it relates to calcium currents. J Membr Biol. 1983;72:117–130. doi: 10.1007/BF01870319. [DOI] [PubMed] [Google Scholar]
- 77.Zucker RS. Short-term synaptic plasticity. Annu Rev Neurosci. 1989;12:13–31. doi: 10.1146/annurev.ne.12.030189.000305. [DOI] [PubMed] [Google Scholar]