Opposite responses of normal hepatocytes and hepatocellular carcinoma cells to substrate viscoelasticity (original) (raw)

. Author manuscript; available in PMC: 2021 Jul 28.

Published in final edited form as: Biomater Sci. 2020 Jan 6;8(5):1316–1328. doi: 10.1039/c9bm01339c

Abstract

The cellular microenvironment plays a critical role in cell differentiation, proliferation, migration, and homeostasis. Recent studies have shown the importance of substrate viscosity in determining cellular function. Here, we study the mechanoresponse of normal hepatocytes and hepatocellular carcinoma cells (HCC) to elastic and viscoelastic substrates using the Huh7 cell line derived from a human liver tumor and primary human hepatocytes (PHH). Unlike PHH and fibroblasts, which respond to viscoelastic substrates by reducing spread area and actin bundle assembly compared to purely elastic substrates of the same stiffness, Huh7 cells spread faster on viscoelastic substrates than on purely elastic substrates. The steady state spread areas of Huh7 cells are larger on viscoelastic substrates, whereas the opposite effect occurs with PHH cells. The viscoelasticity of the microenvironment also promotes motility and multiple long protrusions in Huh7 cells. Pharmacologic disruption of actin assembly makes cells unable to spread on either elastic or viscoelastic substrates. In contrast, upon vimentin perturbation, cells still spread to a limited degree on elastic substrates but are unable to spread on viscoelastic substrates. The time evolution of cell traction force shows large changes in contractile energy on elastic substrates, but the total force generation is the same on both substrates after a 4hr time period. Our data suggest that stress relaxation time scales of the viscoelastic substrate regulate cell dynamics and traction force generation, indicating different binding-unbinding rates of the proteins that form cell attachment sites in HCC cells and normal hepatocytes. These results suggest that liver cancer cells may have different characteristic lifetimes of binding to the substrate in comparison with normal cells, which causes differences in cell spreading and motility within the diseased tissue.

Introduction:

Cellular response to the extracellular matrix (ECM) depends on both the chemical and physical characteristics of the ECM [1]–[6]. ECM physical properties influence cell shape, structure, function, and migration[7]–[10]. Fibroblasts adapt to the extracellular stiffness and rearrange their cytoskeletal organization and thus the cell stiffness [7], [11]. For many, but not all cell types, the higher the substrate stiffness, the more cells spread, upregulate adhesion sites and generate force[1], [12]–[14]. Mechanical features of the ECM affect the proper functioning of cells in organs in vivo [8], [12]. The development of fibrosis, cirrhosis, HCC or any other chronic liver diseases are associated with increased stiffness and excess matrix deposition due to increased expression of collagen, glycosaminoglycans, or proteoglycans during disease progression [15]–[19]. For example, normal liver tissue stiffness is 600 Pa to 4 kPa whereas a diseased liver can stiffen up to 15 kPa or more. The correlation between increased stiffness and biochemical upregulation remains poorly understood due to lack of appropriate in vivo model systems. Biological tissues such as adipose or liver exhibit nonlinear rheology and stiffening under compression, and these characteristics are not reproduced by hydrogels or elastomers commonly used in cell culture or by isolated biopolymer networks such as collagen [20], [21]. Moreover, most biological tissues are not only elastic but have viscous components [22],. but less attention is paid to the viscous component in understanding tissue or cell mechanics, especially during disease progression or in designing biomaterials for cell mechanics studies. In the case of HCC, tissue viscosity increases more than two-fold. Thus, the viscous dissipation within a tissue could be used as an additional potential marker for the diseased state [21], [24]–[27]. For example, brain tissue has a remarkably high viscous component, a nearly two-fold difference between elastic (G’) and viscous (G”) modulus when measured at 1Hz freq. (G” ~150 Pa, G’ ~300 Pa). Whereas, in the case of other tissues such as liver or lungs, the shear loss modulus value G” is 15 % to 20 % of the shear storage modulus G’. Not only tissues but intracellular microenvironments are characterized as viscoelastic and the balance between elastic and dissipative responses changes with diseases[30], [31]. How cell function changes in response to altered viscosity, and if there is any correlation with diseased state at the single cell level, is unknown. Hence, the accurate characterization of viscosity in contributing to cell mechanotransduction or mechanoresponse along with elasticity needs to be established for better comprehension.

Our previous work shows that the dissipative component of the substrate can influence spreading and adhesion of multiple cell types, and can arrest or reverse the differentiation of hepatic stellate cells to a contractile fibroblast phenotype [32]. A theoretical model shows that the response of the cell depends on the relation between the relaxation timescale of the material and the rates of cell adhesion and deadhesion [33], [34]. It is not yet known if changes in viscosity of the cell microenvironment affect normal and diseased cells differently. In particular, the altered metabolic state and cytoskeletal dynamics of cancer cells suggest that they might respond to mechanical dissipation in the substrate differently from normal cells.

Here we compare the responses of primary human hepatocytes and a human hepatocellular cancer cell line Huh7 to changes in the balance between elastic and viscous properties of their substrate. This work quantifies how initial cell spreading dynamics depends upon the viscosity of the substrate and identifies possible molecular players in sensing viscosity. We have presented a quantitative interpretation of viscous dissipation on initial cell spreading dynamics of hepatocellular carcinoma cells (HCC) [35], [36]. Moreover, we have extended our understanding by comparing cell traction force exerted by cells on elastic and for the first time, on viscoelastic substrates. We showed the role of the cytoskeleton in sensing viscosity, especially vimentin which is one of the biomarkers for the epithelial to mesenchymal transition and upregulated in hepatocellular carcinoma [9], [37]–[41].

Results:

A. Viscoelastic material characterization and cell spreading dynamics:

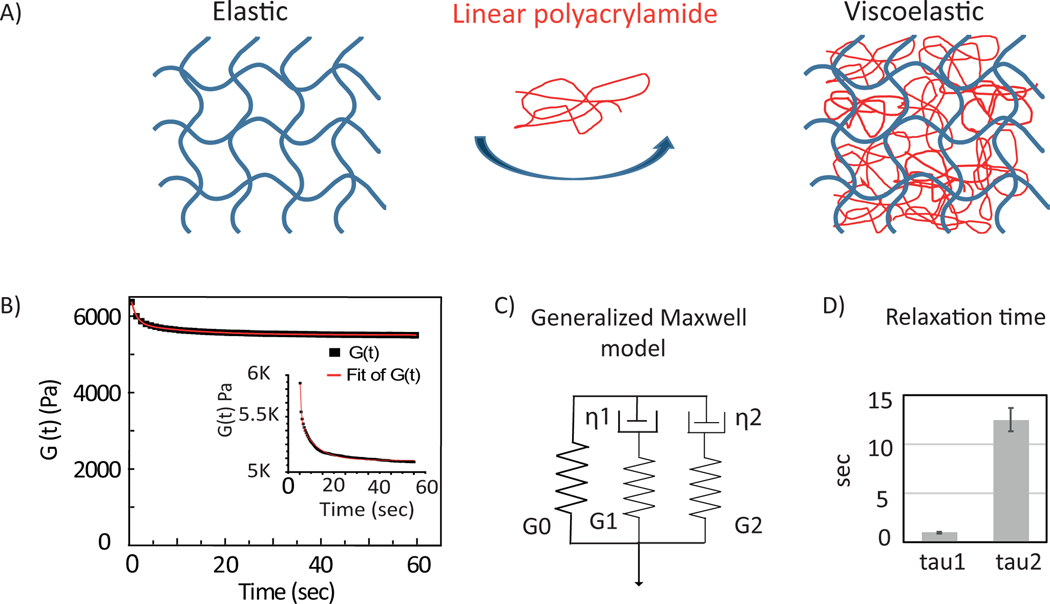
We prepared elastic and viscoelastic hydrogels of constant elastic stiffness G’ (shear storage modulus) = 5 kPa and viscous dissipation quantified by G” (loss modulus) = 0 Pa or 600 Pa at a frequency of 1 Hz. Figure 1.A shows the schematic of the materials used to make viscoelastic substrates. A purely elastic material does not relax whereas viscoelastic material shows spontaneous relaxation. The network with a viscous component exhibits 10% stress-relaxation within 10 s and then reaches a constant, indicating that the material is a viscoelastic solid. Stress-relaxation curves are fit with a generalized Maxwell model as shown in Figure 1.C(middle). G(t)= G0+ G1 e−t/τ1 +G2 e−t/τ2 . G(t) is the time dependent shear modulus of the network. Gi and τi are the shear modulus and the relaxation time of each component respectively. Fitting of the curves show two distinct relaxation time scales in the range of τ1 ~0.9 sec and τ2 ~13 sec (Figure 1.C).

Figure 1:

Figure 1:

Hydrogel characterization. (A) schematic of the materials: elastic cross-linked network of polyacrylamide(left) and viscoelastic network (right) has been made using linear acrylamide(red). (B) Gel polymerization over time (2% strain and 1 rad/sec) showing G’ (light grey) and G” (darker grey). (C) (left) Stress-relaxation of viscoelastic gel (10% strain applied at 1 rad/sec) time in log scale. A typical relaxation curve is fitted with generalized Maxwell model (middle). (right) Averages of two relaxation time scales are shown. Error bars represent standard error of the mean (N=3).

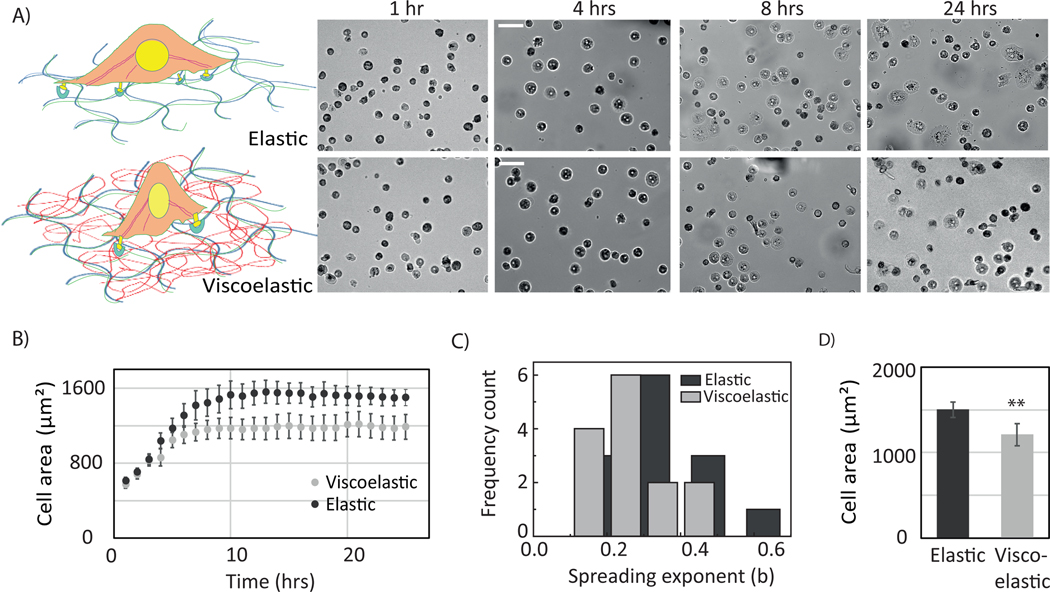
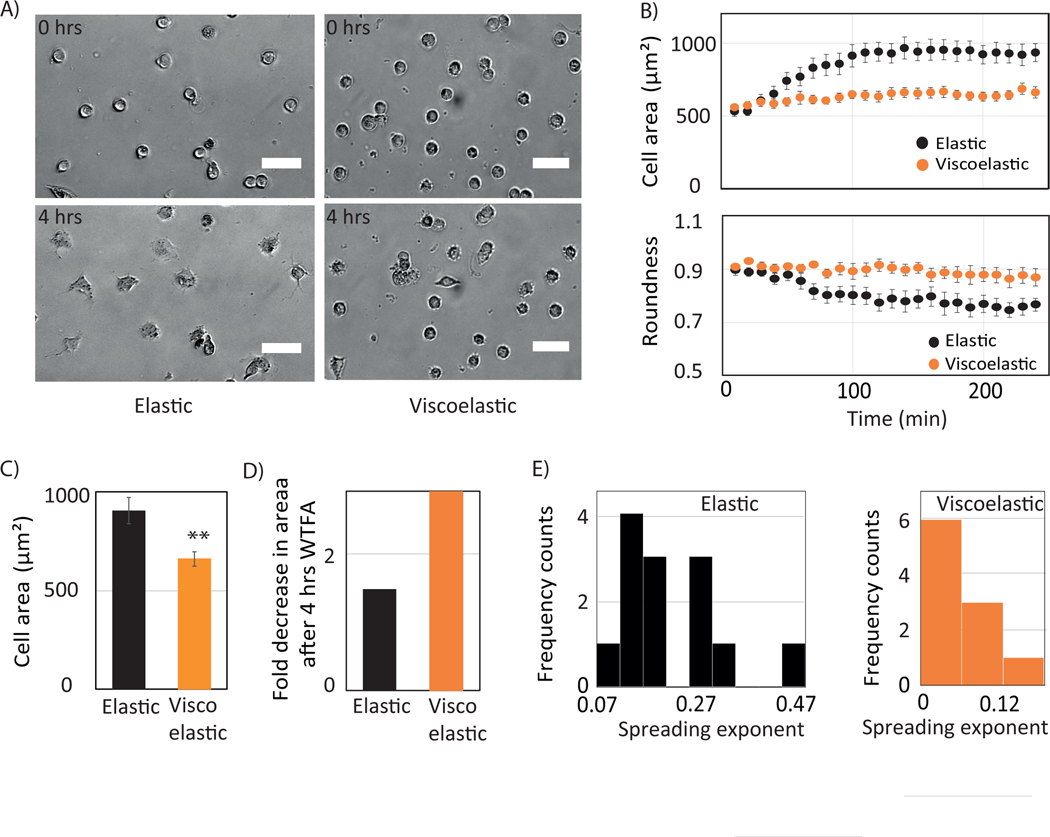
We investigated the response of primary human hepatocytes (PHH) to viscoelasticity. They adhered more weakly and spread less on viscoelastic substrates. This result is consistent with previous findings with fibroblast and hepatic stellate cells. Less than 25% as many hepatocytes made stable adhesions on viscoelastic substrates compared to elastic and glass substrates. Cells on viscoelastic substrate show a biphasic behavior with a mixture of rounded and spread morphologies (Figure S3, S4). The spreading rate of PHH is slower, and they have difficulties to spread on the viscoelastic gel (Figure 2 A, B).

Figure 2:

Figure 2:

Mechanoresponse of PHH cells revealed by viscoelastic gel. (A) schematic of PHH cell response. (lower panel) Cell spreading on elastic and viscoelastic gels (B) Bright-field image of primary human hepatocytes plated on elastic, viscoelastic and glass substrates at 24hrs and 48 hrs. Scale bar, 50 μm. Hepatocyte cell areas on elastic, viscoelastic, and on glass substrates after 24 and 48 hrs. Error bars represent standard error of the mean (for 24 hrs _N_=100, 29 and 104 and for 48hrs N=103, 46 and 102 cells on Elastic, viscoelastic and on glass substrates respectively). p-values are determined from Student’s t-test for unpaired samples ( n.s p > 0.05, * p<0.05; ** p<0.01, *** p<0.001 ).

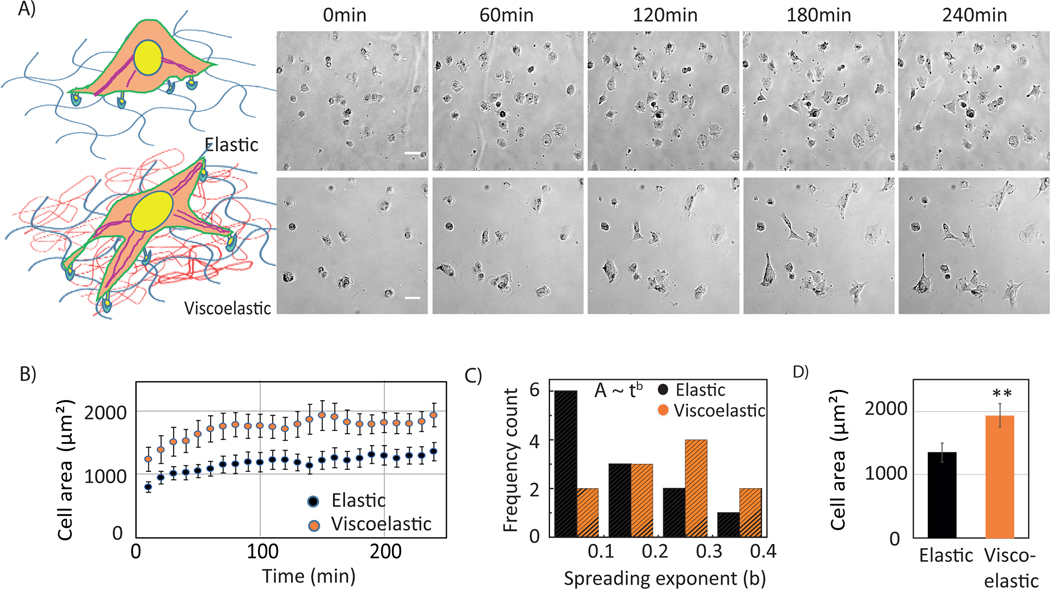
Next, Huh7 cells were plated on elastic and viscoelastic substrates. The values of G’ and G” were chosen in the view of previously measured HCC liver stiffness, which falls in the same range [15]. The schematic represents the hydrogel combination, and the cellular response to it (Figure 3.A). Cell spreading is observed over 4 hours (Figure 3.B). Cells on viscoelastic substrates spread much faster. It is evident from the response of Huh7 cells on viscoelastic substrates that cells do not spread isotropically, and the edge of the membrane is pinned at one end[11]. An elongated cellular morphology and long protrusions are evident on viscoelastic substrates (supplementary movie1, movie2) but are absent in cells on purely elastic substrates.

Figure 3:

Figure 3:

Mechanoresponse of Huh7 cells on elastic and viscoelastic gel substrates. (A) schematic of the materials and cell response. Elastic cross-linked networks (left) and viscoelastic networks (right) have been made using linear (red) and crosslinked (blue) polyacrylamide. Bright-field images of Huh7 cells plated on elastic (upper panel) and viscoelastic (lower panel) substrates. Images are representative of 1 hr time interval (1 hr, 2 hrs, 3 hrs, 4 hrs). Scale bar, 10 μm. (B) Time evolution of cell areas (left) on elastic (black) and viscoelastic (orange) substrates. Error bars represent standard error of the mean (_N_=15 cells on each substrate). (C) Frequency count of exponents obtained from individual cell spreading area growth curve fitting to a power law model. (D) Huh7 cell areas on elastic and viscoelastic substrates after at 4 hrs. Error bars represent standard error of the mean (_N_=15 cells on each substrate substrates respectively). p-values are determined from Student’s t-test for unpaired samples f (** p<0.005; * p<0.05).

In addition, cells spread much faster during the first hour of attachment, followed by a slower spreading rate that reaches a plateau after 3 hrs ( Figure 3.C). To quantitatively measure the spreading dynamics, we have fit the change in area for the first 1.5 hr data with a power law model, A=C tb (where A= spread area, t= time, C= prefactor, b= exponent)[11](Figure S1). The histogram plot of the exponent b shows that the peak occurs at 0.3 or higher for viscoelastic substrates whereas on elastic substrates a sharp peak is observed at value 0.1 or less within the regime of spreading shown in Figure 3.C. However, we lack the early stage of cell spreading in these experiments which would reflect much faster spreading on viscoelastic substrates.

To investigate the molecular mechanism that might account for the opposite responses of PHH and Huh7 cells, we have stained actin, vimentin, microtubules and the nucleus for both cell types (Figure S2). The vimentin and actin in Huh7 cells, both form long filamentous bundles following the cell morphology on viscoelastic substrates, whereas on elastic substrates, a sparse distribution of actin in network like structures is observed. Images show a higher intensity of vimentin near the nucleus of the cell, which is similar to other findings [3], [31]. PHH cells do not have vimentin intermediate filaments. However, they do express keratin as shown in the image (Fig: S4). Images on glass show a distinct actin and microtubule network structure contrary to purely elastic substrates.

B. Huh7 cell motility and traction force measurement:

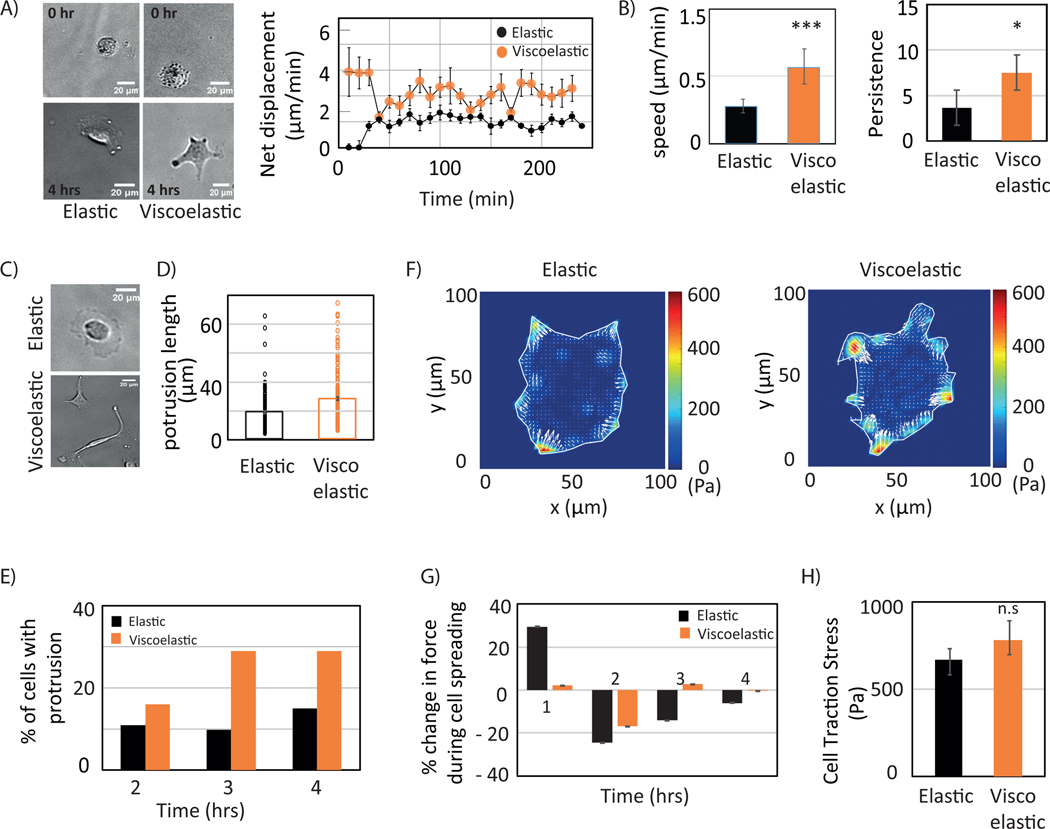
Next, we investigate if viscosity affects cell migration and traction forces for HCC cells. Migration assays show a higher displacement and a 2-fold increase in average cell speed on viscoelastic substrates when calculated over 4 hrs (Figure 4. A, B). Cells start forming protrusions on both these substrates with time as depicted in Figure 4.C (movie2). The percentage of cells with protrusions increases over time (Figure 4.D). The average protrusion length shows a significant difference between the substrates after 4hrs (Figure 4.E). A typical single cell traction contour stress map is shown in Figure 4.F. Over the course of spreading events, forces are calculated at 0.5, 1, 2, 3, and 4 hrs. Traction stresses are normalized with respect to measured stresses at 0.5 hr showing that the stress reaches a maximum by 0.5 hrs on both these substrates (Figure 4.G) and reaches a stable level of traction that is similar for both substrates by 4 hr (Figure 4.H).

Figure 4:

Figure 4:

Huh7 cell dynamics. (A) Bright-field image of Huh7 cell (left) showing cell position at 0 hr. (upper panel) and at 4 hr (lower panel) on elastic and viscoelastic substrate s. Scale bar, 10 μm. Net displacement of cells on elastic and viscoelastic substrates. Error bars represent standard error of the mean (_N_=15 cells on each substrate). Each data point represents 5 mins. (B) Cell migration speed and persistence calculated on elastic (blue) and viscoelastic (green) substrates during a 4hr period. (C) Bright field image of cell protrusions. (D) and (E) cell protrusions are quantified during cell spreading and average protrusion length determined after 4 hrs on both elastic (black) and viscoelastic (orange) substrates (N=80, N=83 cells respectively). Bright field images (left) show protrusion during spreading, percentage of cells with protrusion (middle) quantified every hour over 4 hrs, average protrusion length (right). (F) traction stress map. (G) Cell traction dynamics on both elastic (black) and viscoelastic (orange) substrates (N=13 cells for each). Force percentage calculated with reference to traction force at 30 min. (H) Average cell traction stress after 4hrs calculated on elastic (black) and viscoelastic (orange) substrates with error bars represent standard error of the mean (_N_=23 and N=27 cells on elastic and viscoelastic substrates respectively). p-values are determined from Student’s t-test for unpaired samples with respect to control cells (*** p<0.0001, n.s p> 0.1).

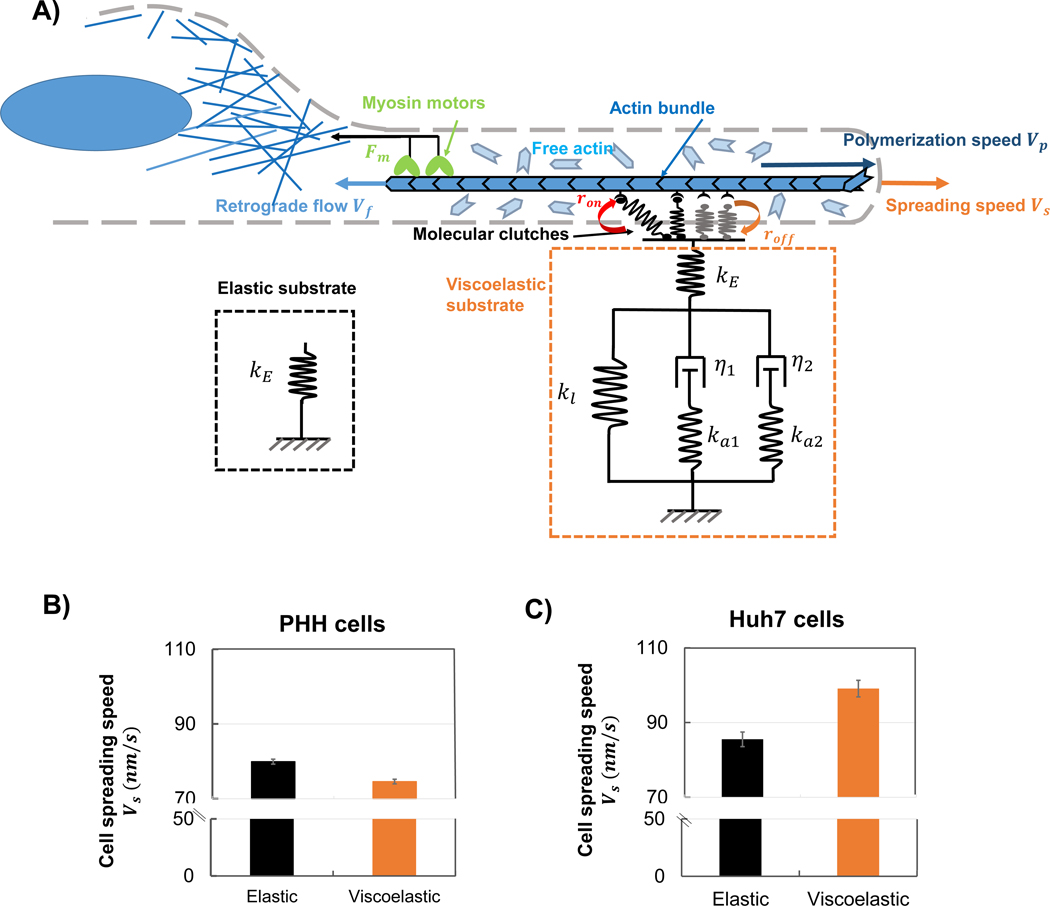
C. Model explains different viscoelastic regulation results for HPP and Huh7 cells

To understand the mechanisms involved in the spreading behavior of HPP and Huh7 cells, we implement our recently developed motor clutch model for cell spreading on viscoelastic materials [42] (Figure 5.A). In this model molecular bonds (clutches) connect actin filaments to the substrate and can randomly break (with dissociation rate roff) and re-engage (with association rate ron). The connected actin filaments are continuously pulled towards the cell center by myosin motors, leading to retrograde flow. Engagement of clutches with the substrate reduces this retrograde flow, which allows polymerization at the leading edge to push the cell membrane forward (eventually resulting in the cell spreading). Here we assume that each individual clutch (adhesive ligand on collagen I) is a slip bond, with a dissociation rate that increases exponentially with the force it transmits. For cells on elastic substrates, these clutches are attached to elastic PAA networks represented by a linear spring with stiffness kE (Figure 5A). On the viscoelastic substrates, the clutches are also attached to the elastic PAA (as only the elastic PAA networks are coated with collagen I). However, this linear elastic component is then in series with a Generalized Maxwell model with two relaxation timescales τs1=η1ka1,τs2=η2ka2, as characterized in Figure 1.C. The parameters for these substrates are identified directly from our experimental relaxation tests (Results A). It should be noted that this new clutch-substrate linking mode (collagen I coated only on elastic PAA networks) differs from our previous work, in which clutches are attached to both elastic and viscous components [36]. Importantly, this arrangement of mechanical components causes cells to sense a smaller effective stiffness on viscoelastic substrates, as the effective stiffness of the viscoelastic substrate (a spring in series with a Generalized Maxwell model) is smaller than the elastic substrate stiffness (i.e. keff<kE). This may be understood in the sense that the effective stiffness of two springs in series is lower than that of either spring alone. Our simulations show that the clutches of PHH cells first form stable adhesions, and then break after a certain (long) time (which we term the adhesion lifetime shown in Figure S5.D) greater than clutch binding timescale (i.e. τlifetime>τbinding). This motor-clutch dynamics with adhesion formation and breakage is also called as the “load and fail” regime [43] (refer to materials and methods), where cell spreading increases with stiffness. Thus, on viscoelastic substrates, as cells sense a lower effective stiffness, adhesions are weaker and offer a lower resistive force to retrograde flow, leading to a low cell spreading area. Our model therefore supports the experimental findings (Figure 3.D) that cell spreading decreases on viscoelastic substrates compared to elastic substrates (Figure 5.B).

Figure 5.

Figure 5.

Model explains the viscoelastic regulation results for different cells. (A) Schematic of motor clutch model for a cell spreading on an elastic or viscoelastic substrate (collagen I coated only on elastic PAA components). Myosin motors pull the actin bundle towards cell center at a retrograde flow velocity Vf. Clutches connect the actin bundle to the substrate based on the reaction rates ron and roff and resist the retrograde flow. The spreading speed Vs is the difference between polymerization speed Vp and retrograde flow Vf. The viscoelastic substrate is represented as a Generalized Maxwell model with two relaxation timescale τs1=η1ka1,τs2=η2ka2. (B-C) Spreading speed Vs of PHH cells (B) and Huh7 cells (C) on elastic (black) and viscoelastic (orange) substrates. Error bars represent the standard deviation (N=10 simulations).

However, this trend is reversed for Huh7 cells, which attain higher spreading areas on viscoelastic substrates (Figure 3D) than on elastic substrates. In Huh7 cells, vimentin intermediate filaments are more extensively expressed than in PHH cells, which can increase the turnover rate of paxillin [9]. To account for this effect in our model, we increase the clutch dissociation rate roff. This reduces the adhesion lifetime (which becomes lower than the clutch binding timescale, i.e. τlifetime<τbinding) and causes the clutches to quickly bind and unbind without forming large stable focal adhesions (Figure S5D). The motor-clutch dynamics is also called “frictional slippage” [43] where retrograde flow is now predominantly regulated by the adhesion lifetime. A reduction in the effective stiffness sensed by the cells, as on viscoelastic substrates, will increase this adhesion lifetime as it has properties of a slip bond. This reduces time-averaged retrograde flow and leads to an increase in cell spreading (refer to materials and methods for detailed explanation). Our simulations therefore support the experimental result that Huh7 cells spread more on viscoelastic substrates (Figure 5.C). Our analysis also provides an explanation for the higher migration rate of Huh7 cells (compared to PHH cells), as they can easily break their weak adhesions (in the frictional slippage regime) to migrate.

D. Role of cytoskeletal filaments in sensing viscoelasticity

The cytoskeleton is known to maintain cellular architecture, morphology and traction stress [1], [44]. Actin is responsible for the force generation, and by polymerization and depolymerization it facilitates cell migration. Recent studies show that the vimentin intermediate filament network maintains cellular architecture by sustaining large deformation[41], [45]. It has also been observed that vimentin can alter cell adhesion by regulating integrin function [38], [46]. To investigate the role of actin and vimentin in cell spreading dynamics and adhesion in response to viscosity, we have used pharmacological drugs latrunculin A and withaferin A (WTFA) to perturb the actin and the vimentin network respectively.

Before seeding cells on the hydrogel, drugs were added to the culture medium, and cell spreading was monitored for 4 hrs (Figure 6. A). When vimentin is perturbed, cells on elastic substrates spread in a slower rate up to certain degree with an initial delay of ~30 mins and reach maximum spreading within 1.5 hours. In contrast, cells on viscoelastic substrates are unable to spread and remain mostly round (Figure 6.B). We have quantified the area difference between control and WTFA-treated cells (Figure 6.C). After 4 hrs of treatment, vimentin-perturbed cells display 1.5-fold and 3-fold decreases in area on elastic and viscoelastic substrates respectively (Figure 6.D). The cell area change is fit with a power law model (A ~ tb). The peak of the exponent values lies between 0.07 and 1.27 for the elastic substrate whereas it is lower than 0.05 on viscoelastic substrates showing a slower spreading rate.

Figure 6:

Figure 6:

Role of vimentin in Huh 7 cell mechanoresponse. (A) Bright-field image of Huh7 cell plated on elastic (upper panel) and viscoelastic (lower panel) substrates when cells are treated with withaferin A at 0 hr and 4 hrs. Scale bar 50 μm. (B) Time evolution of cell area (top) and roundness (bottom) on elastic (blue) and viscoelastic (red) substrates. Error bars represent standard error of the mean (_N_=15 cells on each substrates). (C) Huh7 cell areas at 4 hrs (left) and (D) fold change in areas (right) with respect to control when treated with withaferin A on elastic (blue) and viscoelastic (red) substrates are shown. Error bars represent standard error of the mean (_N_=15 cells on each substrate). p-values are determined from Student’s t-test for unpaired samples f (** p<0.005; * p<0.05). (E) Frequency count of exponent obtained from individual cell spreading area growth curve fitting to a power law model.

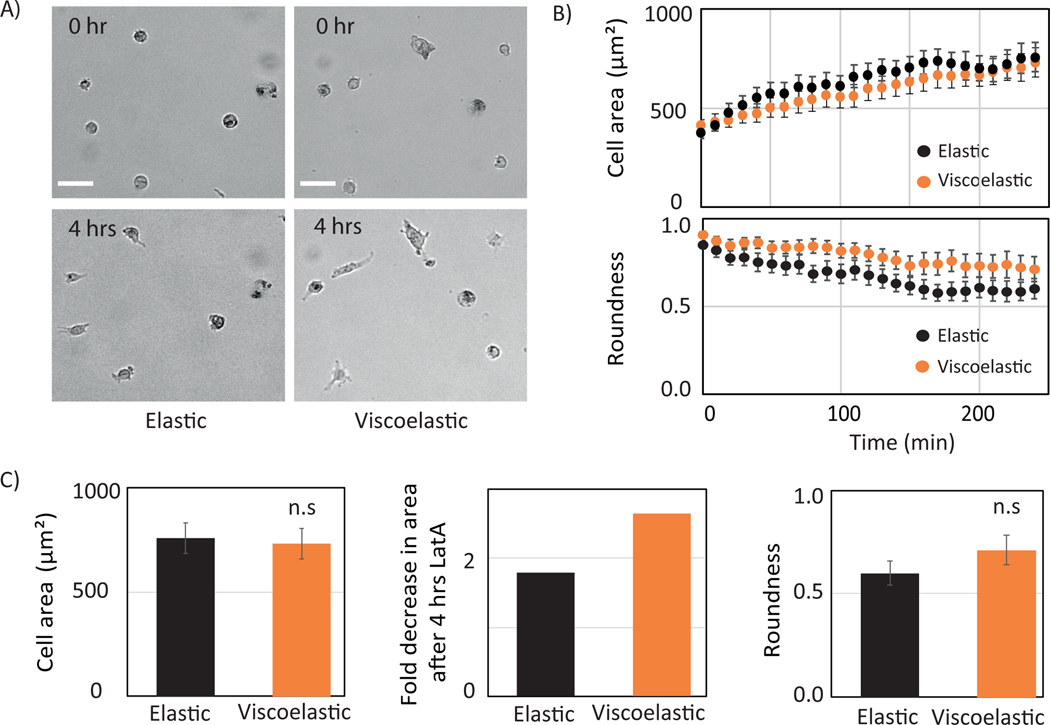
In contrast to the effects of vimentin disruption, actin perturbation affects cell spreading in a similar manner on both the substrates (Figure 7). The spreading rate is slower, and the spread area is smaller on both substrates compared to control (Figure 7. B, C). However, cells are more rounded on the viscoelastic substrate (Figure 7. C). The effect of WTFA and LatA are confirmed by the immunostaining (Figure S3). LatA perturbs the actin network but other networks were unaffected. WTFA perturbs the vimentin network, and there was some effect on actin well, as revealed by immunostaining (Figure S3).

Figure 7:

Figure 7:

Role of actin in Huh 7 cell mechanoresponse. (A) Bright-field image of Huh7 cell plated on elastic (upper panel) and viscoelastic (lower panel) substrate when cells are treated with Latrunculin A at 0hr and 4 hrs. time. Scale bar 100 μm. (B) Time evolution of cell area (top) and roundness (bottom) on elastic (blue) and viscoelastic (red) substrates. Error bars represent standard error mean (_N_=15 cells on each substrate). (C) Huh7 cell area at 4 hrs. (left) and fold change in area (right) with respect to control when treated with Lat A on elastic (blue) and viscoelastic (red) substrate shown. Error bars represent standard error mean (_N_=15 cells on each substrate). p-values are determined from Student’s t-test for unpaired samples f (** p<0.005; * p<0.05).

Discussion

In this work we showed that the spreading dynamics of normal and cancerous cells are differently regulated in response to viscoelasticity. Here we observe two different modes of cell spreading for carcinoma cells. Normal human hepatocyte cell responses are similar to our previous finding with fibroblasts where cell area is smaller on viscoelastic substrates compared to elastic substrates[35]. On the other hand, hepatocellular carcinoma cells show opposite effects compared to normal human hepatocytes. Cells spread more, and higher motility is observed on viscoelastic substrates. These results may explain the correlation between elevated viscosity and metastasis in liver cancer. In addition, cells are more anisotropic at the later stage of spreading and sometimes migrate while pinning one edge of the membrane to the substrate. In contrast, cells on the elastic substrate are less dynamic and exhibit more isotropic spreading. On viscoelastic substrates, membrane pinning at one edge facilitates formation of long protrusion. Our findings are in agreement with others finding that the cell spread area increases with the increase of loss modulus of the substrate for Huh7 cells [47].

The discrepancies between cell types can be explained by the different dynamic regimes of motor-clutches. PHH cells are in the “load and fail” regime (Figure S5.B and S5.D). In this regime clutches first make stable adhesions that break after a given (long) adhesion lifetime, and the adhesion lifetime is greater than the clutch binding timescale (i.e. τlifetime>τbinding). Cells sense a lower effective stiffness on viscoelastic substrates (as described in Results D), and thus the adhesion lifetimes are increased significantly even though adhesion forces are reduced. This facilitates high retrograde flow, and the outcome is a reduction in cell spreading on viscoelastic substrates. In contrast, Huh7 cells are in the “frictional slippage” regime (Figure S5.D) as their higher vimentin expression or other changes in composition and signaling increases the clutch disassociation rate. Here clutches quickly bind and break without forming large stable focal adhesions (i.e. τlifetime<τbinding). In this frictional slippage regime, a lower effective stiffness (as sensed by cells on viscoelastic substrates) extends the adhesion lifetime significantly, stalls the retrograde flow, and leads to an increase in cell spreading on viscoelastic substrates. Interestingly, previous experiments have shown that Huh7 cells migrate faster and have smaller adhesions (with shorter adhesion lifetimes) than PHH cells. This indicates Huh7 cells exhibit frictional slippage dynamics, and in turn validates our model.

It has previously been reported that vimentin promotes cell migration which may be correlated with denser and longer filaments on viscoelastic substrates as shown by immunostaining images [9]. Our results show that the inhibition of vimentin restricts cell spreading on the viscoelastic environment contrary to the elastic substrate. This indicates that the vimentin activity might be important not only to sustain large deformation but also at the leading-edge dynamics and the reinforcement of cell adhesion. Interestingly, when cells are treated with WTFA, cell spreading on elastic substrates is delayed for 30 mins before starting to form adhesion sites, which needs further investigation for better understanding of the mechanism of delay to overcome the perturbation.

Tissue stiffness and viscosity increases in fibrosis or HCC which is contrary to other tissue mechanics. For example, in breast cancer mechanics where malignant tumors are more compliant than benign tumors. In both benign and malignant cases collagen density increases however they are structurally different. In benign tumors proteoglycan content increases in proportion to collagen density but in malignant tumors it decreases[48]. In HCC the amount of glycosaminoglycans (GAG’s) increases which is shown as one of the candidates for increased stiffness[21]. Hence, the biochemical composition in tissue alters the mechanical properties such as G’ and G”. Cells are also more motile in case of cancer.

Our finding confirms that normal and carcinoma cells have different spreading dynamics at the molecular level, which are influenced by the viscosity of the substrate. However, the work is focused only on one cancer cell line and cell substrate interactions are tested for one of the ligand binding protein, collagen I. One of the main technical limitations of this work is the viscosity range which is limited to 10% of the shear modulus value G. To address the question if stiffness itself can overcome the presence of the dissipative component in viscoelastic substrate at higher G’ and G” values, a substrate with higher stiffness and viscosity or the same stiffness and higher viscosity range is needed. However, fabrication of a viscoelastic substrate with high G’ and G” is technically challenging. To achieve the values G” 10% of G’ when G’=30 kPa is not possible with the method used in this study. Fig8.A shows gel polymerization of G’=30kPa and G” =1.5kPa (i.e. G” is 5 % of G’). When higher concentrations of linear acrylamide are added to the solution, the gel phase separates. As a result, expected values of G’ decreases and G” cannot be achieved (Figure 8.B).

Another limitation is the inclusion of the material’s properties in TFM calculation. A proper theoretical framework for traction force measurement, which will include the dissipative component of the substrate, is required. Also, the distribution of force within a cell and the peak of cell traction during cell spreading remains unexplored in these two substrates

Altogether, our results suggest that the use of purely elastic materials to understand cell mechanoresponse in tissue whose function requires nonlinearity, dissipation would not fully describe mechanosensitivity. To approximate biological tissues or to unfold cellular behavior in a diseased state, using viscoelastic substrates would be more appropriate to mimic the mechanical environment of cells. Our data demonstrate that using a dissipative system, normal and cancerous cell mechanics and behavior can be characterized and differentiated. This result indicates that the relaxation time scales regulate HCC cell motility, force generation, intracellular organization and cell substrate interactions differently compared to PHH. The underlying mechanism of increased viscosity in liver metastasis would be important to identify and their possible consequences can now be better characterized using this new class of viscoelastic substrates.

Statistical analysis

Data are expressed as means ± standard error of the mean. Statistical relevance was evaluated using Student’s t-tests and the p-value is indicated (n.s= non-significant, * p<0.05, ** p<0.01, *** p<0.001) otherwise specified.

Materials and Methods:

Hydrogel preparation:

Hydrogels are prepared as described in the previous work[35]. Briefly, for elastic substrate 8% acrylamide and 0.1% bis-acrylamide (Bio-Rad), 2% N-hydroxysuccinimide (dissolved in DMSO) (Sigma), 0.375 % 3-Aminopropylsilyl (Thermo Fisher Scientific), 0.125% tetramethylethylenediamine (Millipore Sigma) added into water to prepare elastic gel of stiffness 5kPa (G’=5kPa and G” =0Pa) and for viscoelastic gel (G’ = 5kPa, G” =600Pa) 14.3 % linear acrylamide (5%stock) and 0.15% bis-acrylamide (instead 0.1%) added to the same protocol as elastic substrate recipe (Fig 1(a)). Gels are laminated with (100 μg/ml) collagen type I (Corning) by incubation overnight at 4 °C.

Rheological Measurement:

Rheology measurements were performed using an RFS3 strain-controlled rheometer fitted with 25 mm diameter parallel plates and a Peltier element incorporated in the bottom plate of the rheometer. For each sample, the gel is directly polymerized between the parallel plates of the rheometer[1]. Time evolution of polymerization is measured for elastic and viscoelastic substrates in 2% strain and 1rad/sec. The equilibrium shear modulus (_G_′ and _G_′′) determined by the plateau (Figure 1.C). Stress-relaxation experiments were performed by applying 10% strain. Stress-relaxation curves were fitted with two component Maxwell model and relaxations times are obtained (using Origin).

Cell Culture, reagents, immunostaining:

Huh7 cells are well differentiated hepatocyte derived cellular carcinoma cell line taken from a liver tumor of a 57-year-old Japanese male in 1982 (The line was established by Nakabayshi, H. and Sato, J). Huh7cells are grown in DMEM 1X (Life Technologies) supplemented with 10% (vol/vol) FBS (GE Healthcare Life Sciences) at 37 °C with 5% (vol/vol) CO2. Before seeding the cells, protein solutions are removed, and hydrogels are incubated with respective medium for 30mins at 37 °C with 5% CO2. Cells are plated at a density of 50,000 cells/gel or less in 100 μl of medium for 22 mm diameter coverslip. Primary human hepatocytes are grown in hepatocyte maintenance medium (MM250) and hepatocyte plating medium (MP100) (TRL). Cells are taken for time lapse imaging immediately after seeding. PHH cells are plated at a density of 100,000 cells/gel or more in 100 to 200 μl of plating medium for 22×22 mm diameter coverslip. To maintain nearly the same cell density as huh7 cells on the gel, PHH cell density was kept higher as not all the cells adhere to the substrate. After 12hrs of culture in plating medium, PHH cells are cultured with maintenance medium.

For immunofluorescence experiments, cells are fixed with 4% paraformaldehyde (Affymetrix) followed by 5% BSA and 1% Saponin (Sigma) for blocking and permeabilization. Primary antibodies are Alexa- Fluor 647 phalloidin (Invitrogen), and anti-vimentin (Novus Biologicals), dapi (Sigma). To perturb actin and the vimentin network, latrunculin A (2μM) and withaferin A (8μM), (Millipore) were added respectively to the culture medium prior seeding the cells on the hydrogels.

Video microscopy and Imaging and Analysis:

Time lapse images of the cell are acquired with Leica DMIRE2 microscope using ivision software. An environmental chamber is used to maintain the temperature at 37 °C and 5% CO2 for live cell imaging. Cell spreading images are acquired at multiple positions at every 5 minutes of time interval for 4-hour time period or more with 10X objective. Cell images after 24 hours are taken with 10X or higher magnification. Immunofluorescence images are acquired with 100X and 40X objective. Image J software is used for cell spreading and the motility assay. Cell area, dynamics, migration and protrusion are calculated using Fiji. Cell speed is calculated by finding the centroid of the cell by manual tracking of Fiji at 10 mins frame rate. A Matlab routine is developed for power law spreading analysis.

Motor clutch model for cell spreading on viscoelastic substrates

We adopted the canonical motor-clutch model to study the impact of viscoelasticity on cell spreading. In this model, myosin motors pull the actin filament bundle towards the cell center, generating retrograde flow of actin. The molecular clutches, connecting the F-actin with the substrate, were assumed to be able to randomly break or re-engage with a dissociation or association rate of roff,i or ron respectively. The master equation describing the evolution of the state of each clutch can be written as:

dPb,idt=1−Pb,iron−Pb,iroff,i , S1

where Pb,i represents the probability for clutch i to remain engaged. As the F-actin slides, a bound clutch (treated as a linear spring with stiffness, kc) undergoes stretching and hence generates a force Fc,i resisting the retrograde flow of actin. If the displacements of the filament- and substrate-end of the clutch are denoted as xc,i and xs, then the force can be expressed as Fc,i= kcxc,i−xs. For slip bonds, the dissociation rate is expected to increase exponentially with Fc,i, that is roff,i=roff0·exp⁡Fc,iFb, where Fb is a characteristic unbinding force and roff0 represents the breaking rate of unloaded clutches.

A generalized Maxwell model with two relaxation timescales was used to fit the rheological data for viscoelastic substrates. Because collagen I is coated only on the elastic network, one extra elastic component (represented by linear spring) was added in series with a Generalized Maxwell model, representing a viscoelastic network (Figure S5.A). The force-displacement relation can be written as:

ka1+ka2+kl+kEkEFs=ka1+ka2+klxs−ka1xη1−ka1xη1;

η1dxη1dt=ka1kEkExs−kExη1−Fs;

η2dxη2dt=ka2kEkExs−kExη2−Fs. S2

Here ka1, η1 and ka2, η2 are the first and second additional stiffness and viscosity respectively corresponding to the first and second relaxation timescales τs1=η1/ka1 and τs2=η2/ka2 (Figure S5.A). xη1 and xη2 are the displacement of first and second dashpot respectively. Since the elastic PAA component is dragged out to directly attach on clutches, the elastic component that is left (spring with stiffness kl) should be less stiff than the elastic PAA networks (spring with stiffness kE). That is kl<kE for viscoelastic PAA substrates. On the other hand, when the left stiffness kl approaches infinite (kl≫kE), the whole model becomes a linear spring with stiffness kE.

The total load from focal adhesion transmitted to the substrate Fs is the sum of all forces sustained by bounded clutches, that is

Based on the Hill’s relation, the substrate force can be related to the retrograde flow speed, Vf,

Where, Nm is the number of myosin motors, Fm refers to the characteristic stalling force, and vu represents the maximum retrograde flow velocity. For a clutch that remains engaged, its filament-end moves with the F-actin, while a broken clutch carries zero load and moves with the substrate (xc,i=xs):

dxc,idt=Pb,iVf+1−Pb,idxsdt. S5

Besides, we were able to relate the cell spreading speed, Vs, to the retrograde flow (Vf) and polymerization velocity (Vp, treated as a constant) as :

By solving all those equations (S1–S6) with the Monte Carlo method, we can simulate the cell spreading speed with time for both elastic and viscoelastic substrates (Figure S5.D). The time-averaged spreading speed is used to characterize the cell spreading. Here we did not include the talin unfolding (clutch reinforcement mechanism) [49]–[51], as the PAA substrates are relatively soft where talin cannot unfold.

We should note here, similar to the case that the effective stiffness of two springs in series is smaller than either of either spring alone, the effective stiffness of the viscoelastic substrate (a spring in series with General Maxwell model) should be smaller than the elastic substrate stiffness (i.e. keff<kE). The stiffness ratio β=kl/kE characterizes how a viscoelastic model behaves close to a pure elastic substrate of stiffness kE. Our simulation shows that, for PHH cells, spreading speed increases as the substrate becomes more elastic (β increases). However, for Huh7 cells, the vimentin intermediate filaments will increase the paxillin turnover rate. This is equivalent to an increased clutch disassociation rate roff0. We also increased the polymerization speed and unloading retrograde flow to account for the high motility and dynamics of Huh7 cells. By implementing this into our model, we can find the reverse viscoelastic regulation effect that cell spreading speed decreases as substrate becomes more elastic (Figure S5.C).

The different cell spreading responses to viscoelasticity are due to the fact that motor-clutches lie in different dynamic regimes. Based on classical motor clutch framework [43], different dynamic behaviors are determined by the competition of two timescales: the clutch binding timescale τbinding and the adhesion lifetime scale τlifetime (Figure S5.D). In the “load and fail” regime, the adhesion lifetime is always larger than binding timescale (i.e. τlifetime>τbinding), and the adhesion force responses to stiffness dominate the regulation. Thus, a higher stiffness increases adhesive forces and resists the retrograde flow more, even though the adhesion lifetime is slightly reduced. This leads to a positive regulation trend that a higher stiffness increases cell spreading. However, in the “frictional slippage” regime, the adhesion lifetime is smaller than binding timescale (i.e. τlifetime<τbinding), and the regulation effect is mainly determined by the adhesion lifetime. A higher substrate stiffness decreases the adhesion lifetime greatly, and thus shortens the adhesion working time on resisting retrograde flow. This causes a larger time-averaged retrograde flow even though the adhesive force is slightly larger, which eventually, leads to a reverse effect that a higher stiffness decreases cell spreading (Figure S5.B).

PHH cells are in the “load and fail” regime [43], since clutches firstly form stable adhesions and break after certain adhesion lifetime longer than clutch binding timescale (i.e. τlifetime>τbinding). In this regime, a lower stiffness (sensed by cells on viscoelastic substrates) decreases adhesion forces greatly, promotes the retrograde flow and eventually decreases cell spreading. However, Huh7 cells are in the “frictional slippage” regime [43], because the higher clutch disassociation rate reduces the adhesion lifetime greatly causing a smaller lifetime scale than clutch binding timescale (i.e. τlifetime<τbinding). In this regime, clutches quickly bind and unbind without forming large stable focal adhesions. Even though single bounded clutch force is smaller on viscoelastic substrates as cells sense a lower effective stiffness, the adhesion lifetimes are increased greatly. This extends the adhesions working time on resisting the retrograde flow, thereby decreasing the time-averaged retrograde flow on viscoelastic substrates. Thus, a lower stiffness (sensed by cells on viscoelastic substrates) decreases the retrograde flow and leads to an increase of cell spreading. All the motor-clutch and substrate parameters can be seen in the Table.S1.

Cell Traction Force Microscopy:

To perform TFM experiments, hydrogel substrates were prepared as described before[1], [6]. In addition, 1% of 200 nm fluorescently labeled green beads (2% solid, Thermo Fisher Scientific) were added to both of the PAA gel solution before leaving it for polymerization. After 24 hrs of plating cells, phase images of the cell, stressed and relaxed images of fluorescently labelled beads were acquired. For the TFM analysis, a custom-built Matlab code was used. At any time, the exerted force can be calculated from the displacement of the bead embedded in the hydrogel [6]. Images of the bead with and without cells are taken. Same Green’s function is used for both elastic and viscoelastic substrate considering that the bead relaxation time is long enough for complete relaxation after detaching the cells from the viscoelastic substrate[52], [53]. The details of the calculation can be found in[52]. From the displacement fields, we calculated cellular contractile forces per unit area using constrained Fourier Transform Traction Microscopy [53]. A displacement field, total strain energy and net contractile moment of the cell were calculated.

Supplementary Material

Fig S1

Fig S2

Fig S3

supplementary data

movie 6

movie 4

movie 5

movie 3

movie 1

movie 2

Figure 8:

Hydrogel characterization. Gel polymerization over time (2% strain and 1 rad/sec) showing G’ (light grey) and G” (darker grey) with increase of linear acrylamide concentration A) 2.5% and B) 3.37%.

Acknowledgements

We thankfully acknowledge Elisabeth E. Charrier for the viscoelastic gel protocol. We thank LiKang Chin for helping with Primary Human Hepatocytes culture. K.M gratefully acknowledges (grant number), A.R was funded by RET and P.A.J acknowledges

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Fig S1

Fig S2

Fig S3

supplementary data

movie 6

movie 4

movie 5

movie 3

movie 1

movie 2