An Empirical Exploration of the (δμ)2 Genetic Distance for 213 Human Microsatellite Markers (original) (raw)
Summary
Microsatellites are now used ubiquitously as genetic markers. One important application is to the assessment of population subdivision and phylogenetic relatedness. Such applications require a method of estimation of genetic distance. Here we examine the most widely used measure of microsatellite genetic distance, Goldstein et al.'s delta-mu squared ([δμ]2), with respect to a large data set of 213 markers typed across samples from four diverse human populations. We find that (δμ)2 yields plausible interpopulation distances. For the first time, we report significant interpopulation differences in mean microsatellite length, although the effect of these differences on (δμ)2 is negligible. However, we also show that the method is extremely sensitive to one or two loci that contribute extreme values, even when a sample size of >200 loci is used. Some of these extreme loci can be removed on the grounds that some alleles carry large indels, but for others there is no clear justification for exclusion a priori. Our data suggest a rather recent African/non-African split, with an upper limit of some 70,000–80,000 years ago.
Introduction
Microsatellites are arguably the most important class of genetic markers yet discovered, being abundant, highly polymorphic, easy to genotype, and predominantly selectively neutral. Uses include gene mapping, parentage analysis and the assessment of relatedness (Queller et al. 1993), phylogenetic studies (Bowcock et al. 1994), studies looking at population differentiation (Paetkau et al. 1995), and, most recently, a means to measure inbreeding (Coltman et al. 1998; Coulson et al. 1998). Microsatellites evolve predominantly by the gain and loss of single repeat units, the so-called stepwise-mutation model (SMM) (Ohta and Kimura 1973), a simple process with well-studied mathematical properties. Such mathematical tractability has led to the development of a range of genetic-distance measures, used widely for examination of the relationships between animal and human populations and with the potential for “genetic absolute dating” (Goldstein et al. 1995_b_).
Goldstein et al.'s (1995_b_) genetic-distance measure (δμ)2 was developed specifically for microsatellite markers and is based on the SMM of evolution. An essential feature of a genetic-distance measure used to estimate relative times of divergence is that its expected value should increase linearly with time. This requirement is fulfilled by the (δμ)2 distance under the unconstrained SMM, and linearity is maintained even when the assumptions of single-step mutations and symmetrical mutation rate are violated (Kimmel et al. 1996). The (δμ)2 distance has a lower variance than does the average square distance (ASD) (Goldstein et al. 1995_a_; Slatkin 1995), from which it is derived, and computer simulations suggest that it is robust to fluctuations in population size (Takezaki and Nei 1996).
When sampling is complete, calculation of (δμ)2 is simple:
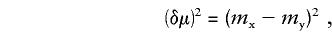
where _m_x and _m_y are the means of allele sizes in populations x and y, respectively. Here and elsewhere, equations are presented for one locus only; data from multiple loci are combined by averaging single-locus (δμ)2 values. Goldstein and Pollock (1997) have suggested the use of _ASD_-Var _x_-Var y as an unbiased estimator of (δμ)2 from an incomplete sample, which we shall refer to as “U(δμ)2”:
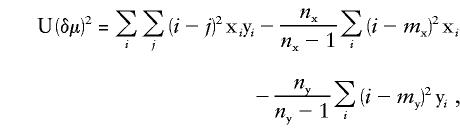
where x_i_ and y_j_ represent the frequency of alleles i and j in each population, Varx and Vary are the variances in allele size in populations x and y, and _n_x and _n_y are the number of alleles sampled from each population. The difference between U(δμ)2 and the squared difference of sample means (henceforth referred to as “M(δμ)2”) “will be very slight unless both the sample size and the level of differentiation is small” (Goldstein and Pollock 1997, p. 340, box C).
Goldstein et al. (1995_b_) have derived the following equation for the expected value of (δμ)2 at τ generations after a single population has divided into two fully isolated populations:
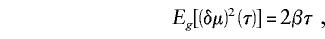
where β is the mutation rate (measured in single-step changes). By substitution of an estimate of the mutation rate, τ can be estimated from (δμ)2.
Despite the attractiveness of (δμ)2 as a measure of genetic distance that is linear over time and independent of population size, there are still only a few published examples of its use on empirical data as opposed to simulation data (e.g., see Goldstein et al. 1995_b_; Goodman 1998).
In the present report we present an exploration of some properties of (δμ)2 in a sample of 213 loci, typed in an average of 294 individuals sampled from four different human populations. We use this large sample to examine the empirical properties of (δμ)2 and its potential for application to population and phylogeny studies.
Material and Methods
Population Samples
DNA samples came from the following human populations: Gambians (_n_=89) from the western region around Banjul, representing the same ethnic groups as Gambians as a whole (Allsopp et al. 1992), Italians (_n_=33) from Padua and its environs, Indians (_n_=182) from Tamil Nadu, and black South Africans (_n_=27) from around the vicinity of KwaZulu Natal. The individuals sampled are regarded as unrelated, being the (unaffected) parents of families analyzed in genome screens.
Choice of Microsatellite Loci
Microsatellite loci were CA repeats typed as part of whole-genome screens for disease-associated regions. Loci were selected from those in the public domain, on the basis of the following criteria: reliable amplification, high (generally >.7) heterozygosity in whites, range of allele sizes that is not inconveniently large, alleles separated by complete repeat units, and no obvious occurrence of null alleles. The loci used for this analysis were distributed throughout the genome, with the exception of chromosomes 4 and 12, which were not available for analysis in our study.
Microsatellite Genotyping
Microsatellites were amplified by PCR using fluorescently labeled primers and were electrophoresed on a denaturing 6% gel in an ABI 373A sequencer. Allele sizes were determined by GENESCAN™ 672 and GENOTYPER™ software (PE Biosystems) and an internal size standard electrophoresed in every lane.
Binning
To convert raw data from the ABI sequencers into numbers of repeat units, a binning macro was written. Allele-length estimates are expected to conform to a series of frequency peaks showing ∼2-bp periodicity and separated by low-frequency troughs. Periodicities are seldom exactly 2 bp, because DNA fragment-size determination is influenced by base composition and, at most loci, a change in repeat number also changes the average base composition of the fragment, causing a slight but detectable shift in its mobility. To allow for this, our macro searches for the strongest periodicity in the data, seeking to minimize the mean squared deviation (MSD) for all empirical allele lengths, from the centers of their nearest bin classes. For the vast majority of loci, binning is unambiguous, with adjacent frequency peaks being separated by gaps in which allele lengths are not observed. However, the MSD values allowed us to identify eight loci where the binning process is unexpectedly poor. Such cases appear to be due to the presence of alleles that differ, in size, by 1 bp. Given the small number of alleles and loci involved, as well as the small impact that such changes will have on mean length (alleles in an intermediate size class will tend to fall equally into bins 1 bp above and 1 bp below their true sizes, giving a zero net change in mean length), we argue that these misclassifications will have a negligible effect on our calculations of genetic distance.
Results and Discussion
Method of Calculation of (δμ)2
In the Appendix, we consider several alternative methods for calculation of (δμ)2, which aim to reduce biases associated with finite sample sizes. In practice, the differences between methods seem to be small. Therefore, hereafter we will use only the simplest form, which we term “M(δμ)2,” calculated as the squared difference in mean length.
Distribution of (δμ)2 Values
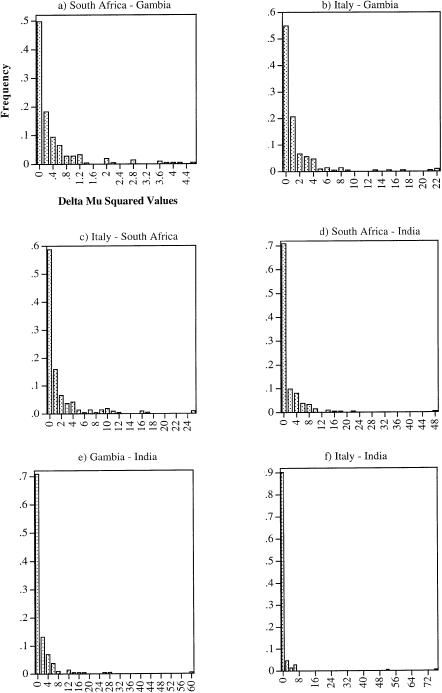
The distributions of M(δμ)2 values for each population pair (fig. 1) are all L-shaped, with many small values and a few much larger ones. Variance in M(δμ)2 is higher than would be expected according to Goldstein and Pollock (1997, referring to Zhivotovsky and Feldman 1995) (table 1), with the observed variance lying outside the 95% confidence interval (CI) for the expected variance for each population comparison except Gambian–South African. The discrepancy is particularly large for comparisons involving the Indian population. Zhivotovsky and Feldman (1995) have argued that the expected variance of (δμ)2 is so large that several hundred microsatellite loci may be required to build trees with reliable branch lengths. The even higher variances that we find imply that even larger numbers of loci are required, unless some alternative approach for calculation of genetic distance can be found.
Figure 1.
Size distribution of M(δμ)2 over 213 loci. a, Gambian–South African interval size 0.2. b, Gambian-Italian, interval size 1. c, Italian–South African, interval size 1. d, Indian–South African, interval size 2. e, Gambian-Indian, interval size 2. f, Indian-Italian, interval size 2.
Table 1.
Mean, Variance, and Expected Variance for M(δμ)2, for Six Population Comparisons
| M(δμ)2 | |||
|---|---|---|---|
| Populations Compared | Mean (95% CIa) | Variance | Expected Variance (95% CI)b |
| Gambian–South African | .481 (.372–.589) | .651 | .463 (.278–.695) |
| Indian-Italian | 1.344 (.456–2.212) | 41.820 | 3.612 (.452–9.789) |
| Gambian-Italian | 1.897 (1.428–2.367) | 11.730 | 7.200 (4.132–11.114) |
| Italian–South African | 2.117 (1.603–2.632) | 14.662 | 8.967 (5.141–13.852) |
| Indian–South African | 2.426 (1.788–3.065) | 22.624 | 11.774 (6.390–18.790) |
| Gambian-Indian | 2.436 (1.686–3.187) | 31.248 | 11.871 (5.682–20.314) |
Some of the excess variance in (δμ)2 is likely to be due to interlocus mutation-rate variation (Zhivotovsky and Feldman 1995) and possible differences in range constraints (Feldman et al. 1997; Pollock et al. 1998). However, as seen in figure 1, although the majority of (δμ)2 values are clustered at the low end of the size range, there are a few loci that yield very large (δμ)2 values, which dramatically inflate the variance, especially for comparisons involving the Indian population. Two loci in particular contribute extreme values: the largest (δμ)2 is 76.69 for locus DXS993, followed by 53.39 for D6S279. The arithmetic mean (δμ)2 calculated over all 216 loci is 1.34, but it is only 0.99 if DXS993 is excluded. If D6S279 is also excluded, the mean (δμ)2 is reduced further, to just 0.74. This example clearly illustrates how the chance sampling of a particular locus can have a large effect on the mean (δμ)2.
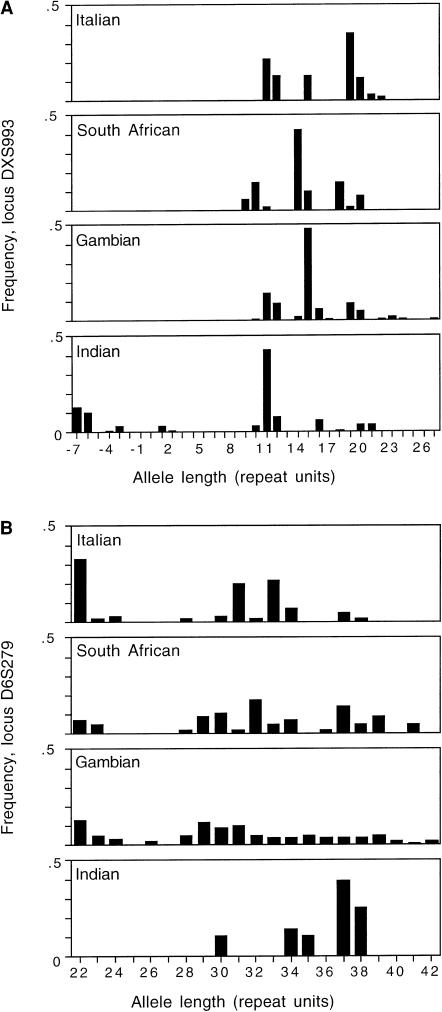
To examine the basis of these extreme values, allele-frequency distributions for DXS993 and D6S279 are compared for all four populations (fig. 2). Locus DXS993 shows evidence of a large deletion specific to the Indian population, which contains some alleles that are shorter than the clone sequence without its microsatellite. Such loci could be removed from the data set on a priori grounds. By contrast, at locus D6S279 the Indian population lacks the lowest mode carried by the other three populations. Such a situation could conceivably arise by drift alone, and hence this locus cannot be excluded a priori. In this particular case, only 14 of 182 samples amplified, suggesting a possible alternative explanation—that short alleles in the Indian population are descended from a progenitor allele that suffered a mutation in one of the priming sites, either reducing or eliminating amplification. Such a mutation would either have to have arisen early in this population's ancestry or have to have spread remarkably fast to achieve its current high frequency.
Figure 2.
Allele-frequency distributions for the two loci contributing the largest (δμ)2 values. A, DXS993. B, D6S279. All allele lengths were binned (see text) and converted to whole numbers of repeat units by subtraction of the flanking sequence, taken as the length of the clone sequence between and including the primer sequences minus the length of the repeat tract in the clone sequence.
Thus, although some loci associated with large (δμ)2 values may be excluded because of alleles carrying obvious deletions, other loci are more problematic. To deal with the latter, one could, through a combination of allele sequencing (to reveal insertions, deletions, and interruption mutations) and redesign of primers (to reveal nonamplifying alleles), assess the nature of those alleles which contribute most to large (δμ)2 values. However, such experiments tend to be extremely time-consuming and are not guaranteed to be successful. Since post hoc exclusion of loci yielding excessively large (δμ)2 is difficult both to justify and to execute (where does one draw the line?), we examined several alternative methods for calculation of overall (δμ)2 values across all loci (table 2).
Table 2.
Averages of (δμ)2 Values Calculated by Various Methods
| Average (δμ)2 | |||||
|---|---|---|---|---|---|
| Populations Compared | Mean | Median | TruncatedMean | AsymmetricallyTruncated Mean | Loci Elimination(No. of LociEliminated)a |
| Gambian–South African | .481 | .200 | .403 | .322 | .481 (0) |
| Indian-Italian | 1.344 | .255 | .662 | .496 | .617 (5b) |
| Gambian-Italian | 1.897 | .713 | 1.507 | 1.236 | 1.802 (1c) |
| Italian–South African | 2.117 | .660 | 1.727 | 1.403 | 2.008 (1d) |
| Indian–South African | 2.426 | .817 | 1.935 | 1.623 | 2.205 (2e) |
| Gambian-Indian | 2.436 | .920 | 1.803 | 1.462 | 2.035 (1f) |
Mean
As shown above, even when >200 loci are examined, (δμ)2 for an individual locus can be so large that its exclusion can reduce the mean value by 26%. Since inclusion of such extreme loci is a matter of chance, the simple mean is prone to remarkable uncertainty. Furthermore, the extent of this uncertainty will be apparent only when an extreme locus is included.
Median
The median (or middle value) is often a more representative measure of the location of a distribution than is the mean, especially when the distribution is asymmetric (Sokal and Rohlf 1995). Median values are considerably smaller than the mean values, but the rank order of size of the medians and means are almost identical, the exception being those for the Gambian-Italian and Italian-South African distances, whose ranks are reversed depending on the measure used. The median may be useful as a comparative measure, but it cannot be used directly, because it will underestimate divergence times.
Least-squares methods
Pollock et al. (1998) have proposed the measures _D_LS and _D_GLS to find the best-fit distance from the (δμ)2 values generated over a number of loci. These methods show improved accuracy over (δμ)2, by allowing for interlocus variation in both range constraints and mutation rate. However, from the data, it is difficult to obtain good estimates of these parameters: the populations have not diverged sufficiently to yield independent samples of the range constraint, and individual loci may not be at mutation-drift equilibrium (either because of recent changes in population size or because of selection at adjacent sites). Computer simulations suggest that _D_LS is less accurate than (δμ)2 and that, although _D_GLS is slightly more accurate than (δμ)2 when interlocus mutation rate varies, (δμ)2 is the most accurate measure when there is variation in locus ranges (Pollock et al. 1998). Until reliable estimates of per-locus mutation rate and range can be made, the justification for using these alternative measures is unclear.
None of the methods discussed above exclude exceptional loci. However, if outlying loci deviate from the SMM model on which (δμ)2 relies, such loci can be legitimately excluded from genetic-distance estimates. The following methods offer alternative exclusion protocols.
Truncated mean
A truncated mean can be calculated by ignoring the most extreme 5% of the distribution. The largest 2.5% (_n_=5) and smallest 2.5% of (δμ)2 values for each population pair are eliminated, and the arithmetic mean is calculated from the remaining 203 values. Truncated means are smaller than the simple arithmetic means but larger than the medians. The rank order of truncated means is similar to that for the means, although the position of the two largest distances (Indian–South African and Gambian-Indian) is reversed between the two measures. The theoretical validity of this method is dubious because we have no grounds on which to exclude the smallest values in the sample.
Asymmetrically truncated mean
This statistic is calculated as for the truncated mean, but with the full 5% of values excluded from the top end of the distribution. The rank orders for asymmetrically and symmetrically truncated means are identical, and their magnitudes are intermediate between the median and the truncated mean. However, 5% is clearly an arbitrary cutoff.
Elimination of loci, to reach predicted variance levels
This method relies on comparisons between the observed and expected interlocus variance (Zhivotovsky and Feldman 1995) in (δμ)2 for a given population pair. For each pair of populations, loci contributing the largest (δμ)2 were removed sequentially until the observed variance lay within the upper CI of the expected variance. The mean (δμ)2 of the remaining loci was taken as a measure of overall (δμ)2. In practice, as many as five loci were excluded per population pair (see the values in parentheses in table 2), and the resulting rank order was the same as that for the truncated means. This approach is attractive because use of the expected variance provides an objective method of deciding how many loci to exclude. However, some of the extra variance may be due to interlocus variation in both mutation rate and range constraints (Zhivotovsky and Feldman 1995; Feldman et al. 1997; Pollock et al. 1998). Therefore, this method may overestimate the number of loci that should be excluded because of non-SMM events.
Effects of General Interpopulation Length Differences
There have been several reported instances of interspecies comparisons of homologous microsatellite lengths such that one species carries longer repeat arrays than another. Part of the difference can be ascribed to an ascertainment bias, arising from the fact that marker loci tend to be developed from unusually long arrays cloned from one species only (Ellegren et al. 1995). However, several reciprocal tests have shown that nonartifactual length differences do exist: humans have longer (CA) repeats than do chimpanzees (Rubinsztein et al. 1995_a_, 1995_b_; Cooper et al. 1998), and sheep have longer (CA) repeats than do cows (Crawford et al. 1998). Such observations contravene an implicit assumption of (δμ)2—that is, that grand mean allele length (i.e., the mean of all loci considered) does not vary among taxa.
Comparisons between grand mean allele lengths among the four human populations that we studied reveal very small but statistically significant differences between the Italians and each of the two African populations and between the Indians and the South Africans: Italian, mean 211.720 bp; Indian, mean 211.653 bp; Gambian, mean 211.253 bp; and South African, mean 211.214 bp; Gambian-Italian, _P_=.013; Italian–South African, _P_=.01, and Indian–South African, P_=.039 (probabilities are from two-tailed paired t_-tests). Since most of the markers are derived from whites, the generally greater length of Italian microsatellites could be due entirely to ascertainment bias. On the other hand, both the significant difference between Indians and South Africans and extrapolation from our previous human-chimpanzee comparisons (Cooper et al. 1998) suggest that nonartifactual length differences probably do exist. Until tests are conducted with markers developed from DNA from nonwhites, the relative contribution of artifact and nonartifact remains unclear; but, if the differences are genuine, they imply that human populations differ slightly in their genomewide microsatellite-mutation rates (Rubinsztein et al. 1995_a_; Cooper et al. 1998). Statistical removal of the observed differences in mean length does not have a significant impact on (δμ)2 values (data not shown).
Observed Heterozygosity and (δμ)2
Loci with high mutation rates are expected to yield larger (δμ)2 values than are given by loci with lower mutation rates (Goldstein et al. 1995_b_). Since mutation rate also correlates positively with heterozygosity, loci with high heterozygosity should also yield relatively large (δμ)2 values. To examine whether this relationship exists, we looked for correlations between locus-specific heterozygosity and locus-specific (δμ)2 values, in each of the possible interpopulation comparisons (table 3) (to standardize comparisons, the heterozygosity of a locus is always taken as its heterozygosity in the Italians, the population closest to the one from which the majority of loci were derived). We find a significant positive correlation in each interpopulation comparison except in that between Italians and Indians (table 3). Repeating the analysis without the loci listed in table 2 gave very similar Spearman rank-correlation coefficient (_r_S) values and unchanged levels of significance (data not shown).
Table 3.
Association between (δμ)2 and Italian Heterozygosity, as Assessed by **r**S and Student's **t**-Test
| Populations Compared | _r_S | t | Pa |
|---|---|---|---|
| Gambian–South African | .189 | 2.809 | <.01 |
| Indian-Italian | .001 | .018 | NS |
| Gambian-Italian | .192 | 2.856 | <.01 |
| Italian–South African | .199 | 2.960 | <.01 |
| Indian–South African | .259 | 3.920 | <.01 |
| Gambian-Indian | .137 | 2.014 | <.05 |
These results emphasize the danger of assuming a single mutation rate for all loci when population-divergence times are calculated from (δμ)2. If loci have been selected for very high heterozygosities, the (δμ)2 values are likely to reflect a higher underlying mutation rate. Alternatively, if loci are selected for proximity to candidate disease genes, a lower mutation rate may be required in calculations.
Combining of Populations
In view of the increasing consensus that the deepest split in the phylogeny of modern human populations occurs between Africans and non-Africans (Cavalli-Sforza et al. 1992; Nei and Takezaki 1996), it would be interesting to date this division by means of the (δμ)2 distance measure. However, to study this split, it is necessary to decide how to combine the information arising from each population. As Goldstein et al. (1995_b_) have discussed, there are two extreme methods: (1) consider each population separately and then take the average of the distances between African and non-African populations or (2) combine the African populations and compare this artificial population with the combined non-Africans. Neither approach is satisfactory, since the first may act to inflate the distance whereas the second is likely to underestimate it. With our data, we explored both approaches (table 4). Our results reflect the predictions by Goldstein et al. (1995_b_)—that method 1 gives larger distances than method 2. However, the differences, between overall (δμ)2, between the two methods, when calculated on the basis of median, truncated means, and eliminated loci, are quite small.
Table 4.
(δμ)2 Values between African and Non-African Populations
| (δμ) | |||||
|---|---|---|---|---|---|
| Populations Compared | Mean | Median | TruncatedMean | AsymmetricallyTruncated Mean | Loci Elimination(Mean No. of LociEliminated) |
| Calculated for Each Population Pair Separately and Then Averaged | |||||
| African-Italian | 2.007 | .687 | 1.617 | 1.320 | 1.905 (1) |
| African-Indian | 2.431 | .869 | 1.869 | 1.542 | 2.120 (1.5) |
| Gambian–non-African | 2.167 | .817 | 1.655 | 1.349 | 1.919 (1.5) |
| Non-African–South African | 2.272 | .739 | 1.831 | 1.513 | 2.016 (1.00) |
| African–non-African | 2.219 | .778 | 1.743 | 1.431 | 2.012 (1.25) |
| Calculated after Data Have Been Merged to Create Composite"African" and "Non-African" Sample Sets | |||||
| African-Italian | 1.887 | .657 | 1.510 | 1.231 | 1.785 (1) |
| African-Indian | 2.311 | .819 | 1.760 | 1.462 | 2.061 (1) |
| Gambian–non-African | 1.831 | .786 | 1.480 | 1.203 | 1.722 (1) |
| Non-African–South African | 1.936 | .640 | 1.604 | 1.323 | 1.832 (1) |
| African–non-African | 1.763 | .670 | 1.429 | 1.178 | 1.666 (1) |
Absolute Dating
An attractive feature of (δμ)2 is that it can potentially be used to make direct estimates of the times since population divergence (Goldstein et al. 1995_b_) if the mutation rate is known. The relationship between (δμ)2 and time is expected to remain approximately linear for ∼250,000 years (Pollock et al. 1998), making it suitable for examination of even deep splits between human populations. To calculate 95% CIs for each locus, 1,000 bootstrap samples were taken from the 213 loci (table 5). Note that the variance portrayed in these CIs does not include any uncertainty in the estimate of the mutation rate.
Table 5.
95% CIs for (δμ)2, and Corresponding Dates
| Populations Compared | 95% CI for (δμ)2 | 95% CI for Date (Mean Date)a |
|---|---|---|
| Gambian–South African | .373–.589 | 9,000–14,200 (11,600) |
| Indian-Italian | .674–2.341 | 16,200–56,400 (32,400) |
| Gambian-Italian | 1.506–2.389 | 36,300–57,600 (45,700) |
| Italian–South African | 1.611–2.644 | 38,800–63,700 (51,100) |
| Indian–South African | 1.864–3.164 | 44,900–76,300 (58,500) |
| Gambian-Indian | 1.808–3.329 | 43,600–80,300 (58,700) |
| African–non-African (method 1) | 1.697–2.882 | 40,900–69,500 (53,500) |
| African–non-African (method 2) | 1.391–2.221 | 33,500–53,500 (42,500) |
The (δμ)2 estimate of the date of population division is more recent than estimates based on other methods. For example, archaeological evidence suggests that the African–non-African divergence occurred ∼100,000 years ago, compared with our estimates of ⩽69,500 years ago (pooled African/non-African data) or ⩽80,300 years ago (the Gambian-Indian distance). When the archaeology is taken at face value, two possible explanations for this discrepancy are the following: (i) our loci have unusually low mutation rates, or (ii) interpopulation migration has reduced population differentiation. Migration patterns may become clearer in light of data from uniparental markers such as mtDNA and Y-chromosome polymorphisms, but, because of the paucity of mutations in pedigrees, the extent of interlocus mutation variation is unlikely to be clarified by direct observation. An alternative approach might be to estimate mutation rates indirectly, through measurement of either effective population size or allele size ranges (e.g., see Feldman et al. 1997; Pollock et al. 1998). Clearly, further work is needed.
Conclusions
We have conducted an extensive analysis of the genetic-distance measure (δμ)2, using >200 microsatellite markers typed across a large number of individuals drawn from four human populations. Our data have yielded plausible although rather recent estimates of the divergence times between these populations, but they also illustrate some potential problems that can arise.
An implicit assumption of (δμ)2 is that mean length across all loci does not differ between populations. However, several recent interspecific studies contradict this assumption (Rubinsztein et al. 1995_a_, 1995_b_; Cooper et al. 1998; Crawford et al. 1998). For the first time, we have shown that small but significant interpopulation differences also exist within a species. Pragmatically, these length differences appear to be too small to have an impact on (δμ)2 values, but their existence may have important implications for our understanding of microsatellite evolution and may imply subtle shifts in the genomewide microsatellite-mutation rate.
The biggest problem that we have identified involves outlying values. As expected, the distribution of (δμ)2 has a very long tail. However, a few loci contribute (δμ)2 values large enough to dominate the overall mean and to create very wide CIs, even among >200 loci. Some of these deviate from the SMM by carrying deletions and could be excluded, but others give high values even though the SMM cannot be rejected. We have examined a number of alternative methods for calculation of the overall (δμ)2, including various truncation strategies and the use of median instead of mean. The rank order of interpopulation distances is generally stable, and truncation improves the CIs. However, in the absence of theoretical grounds for choosing one method over another, we cannot make firm recommendations. More work is needed to establish the statistical properties of these alternative measures.
Our analyses have indicated appreciable interlocus variation in mutation rate. We have shown that (δμ)2 and heterozygosity are correlated and, by implication, that genetic distances will not be directly comparable if they are based on subsets of loci that differ in average heterozygosity. Such lack of comparability will be in addition to any effects due to the chance inclusion or exclusion of loci contributing extreme values. Problems of this nature emphasize the value of reporting in vivo mutations observed in genome screens, since these provide the most direct way to learn more about locus-specific mutation rates.
Acknowledgments
We thank C. Ruwende, K. McAdam, H. Whittle, M. Thursz, S. Best, L. Zhang, S. Meisner, S. Fisher, R. Pitchappan, K. Balukrishnan, and D. Wilkinson for assistance in sample collection and genotyping. Genome screens were funded by the Wellcome Trust. This analysis was funded by Leverhulme Trust grant F/752/A. D.C.R. is a Glaxo Wellcome Research Fellow.
Appendix
The (δμ)2 distance was calculated for each locus and population pair, both as the squared difference in mean length, M(δμ)2, and by the unbiased estimator, U(δμ)2. Of 1,278 locus-population comparisons, 353 (27.6%) generate a negative value of U(δμ)2 (largest negative value of −1.04), because of high intrapopulation variances relative to interpopulation differentiation. The values of M(δμ)2 and U(δμ)2 are highly correlated: Pearson's r varies from .965 (Gambian–South African distances) to >.999 (Gambian-Indian distances). However, U(δμ)2 is smaller than M(δμ)2 in every comparison made (_n_=1,278), with an average difference of 0.183.
The tendency of U(δμ)2 to generate low values can be ameliorated by use of “biased” measures of variance (i.e., those uncorrected for incomplete sampling), to yield a new measure, B(δμ)2, which gives results very similar to those for M(δμ)2:
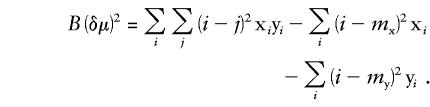
Use of biased estimators of variance in B(δμ)2 can be justified because bias associated with small samples causes underestimation of both the true population variance and the ASD. It is important to note that U(δμ)2 corrects only the population-sampling variance and, consequently, yields distances that are a little too small. In contrast, in B(δμ)2 the opposing biases tend to cancel each other out. Comparisons between B(δμ)2 and M(δμ)2 show that B(δμ)2 is sometimes larger and sometimes smaller than M(δμ)2. Analysis of three independent population comparisons (Gambian-Indian, Gambian–South African, and Italian–South African) has shown that, on average, B(δμ)2 values do not differ significantly from M(δμ)2 values (mean difference 4.436×10-5, _n_=639, _t_=1.919, two-tailed _P_=.055). Thus, in the absence of contraindications, M(δμ)2 is preferred, for its simplicity of calculation.
References
- Allsopp CEM, Harding RM, Taylor C, Bunce M, Kwiatkowski D, Anstey N, Brewster D, et al (1992) Interethnic genetic differentiation in Africa: HLA class I antigens in The Gambia. Am J Hum Genet 50:411–421 [PMC free article] [PubMed]
- Bowcock AM, Ruiz Linares A, Tomfohrde J, Minch E, Kidd JR, Cavalli-Sforza LL (1994) High resolution trees with polymorphic microsatellites. Nature 368:455–457 [DOI] [PubMed]
- Cavalli-Sforza LL, Menozzi P, Piazza A (1992) The history and geography of human genes. Princeton University Press, Princeton [Google Scholar]
- Coltman DW, Bowen WD, Wright JM (1998) Birth weight and neonatal survival of harbour seal pups are positively correlated with genetic variation measured by microsatellites. Proc R Soc Lond B Biol Sci 265:803–809 [DOI] [PMC free article] [PubMed]
- Cooper G, Rubinsztein DC, Amos W (1998) Ascertainment bias cannot entirely account for human microsatellites being longer than their chimpanzee homologues. Hum Mol Genet 7:1425–1429 [DOI] [PubMed]
- Coulson TN, Pemberton JM, Albon SD, Beaumont M, Marshall TC, Slate J, Guiness FE, et al (1998) Microsatellites reveal heterosis in red deer. Proc R Soc Lond B Biol Sci 265:489–495 [DOI] [PMC free article] [PubMed]
- Crawford AM, Kappes SM, Paterson KA, de Gotari MJ, Dodds KG, Freking B, Stone RT, et al (1998) Microsatellite evolution: testing the ascertainment bias hypothesis. J Mol Evol 46:256–260 [DOI] [PubMed]
- Ellegren H, Primmer CR, Sheldon BC (1995) Microsatellite `evolution': directionality or bias? Nat Genet 11:360–362 [DOI] [PubMed]
- Feldman MW, Bergman A, Pollock DD, Goldstein DB (1997) Microsatellite genetic distances with range constraints: analytic description and problems of estimation. Genetics 145:207–216 [DOI] [PMC free article] [PubMed]
- Goldstein DB, Linares AR, Cavalli-Sforza LL, Feldman MW (1995_a_) An evaluation of genetic distances for use with microsatellite loci. Genetics 139:463–471 [DOI] [PMC free article] [PubMed]
- ——— (1995_b_) Genetic absolute dating based on microsatellites and the origin of modern humans. Proc Natl Acad Sci USA 92:6723–6727 [DOI] [PMC free article] [PubMed]
- Goldstein DB, Pollock DD (1997) Launching microsatellites: a review of mutation processes and methods of phylogenetic inference. J Hered 88:335–342 [DOI] [PubMed]
- Goodman S (1998) Patterns of extensive genetic differentiation and variation among European harbor seals (Phoca vitulina vitulina) revealed using microsatellite DNA polymorphisms. Mol Biol Evol 15:104–118 [DOI] [PubMed]
- Kimmel M, Chakraborty R, Stivers D, Deka R (1996) Dynamics of repeat polymorphisms under a forward-backward mutation model: within-population and between-population variability at microsatellite loci. Genetics 143:549–555 [DOI] [PMC free article] [PubMed]
- Nei M, Takezaki N (1996) The root of the phylogenetic tree of human populations. Mol Biol Evol 13:170–177 [DOI] [PubMed]
- Ohta T, Kimura M (1973) The model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a genetic population. Genet Res 22:201–204 [DOI] [PubMed]
- Queller DC, Strassmann JE, Hughes CR (1993) Microsatellites and kinship. Trends Ecol Evol 8:285–288 [DOI] [PubMed] [Google Scholar]
- Paetkau D, Calvert W, Stirling I, Strobeck C (1995) Microsatellite analysis of population structure in Canadian polar bears. Mol Ecol 4:347–354 [DOI] [PubMed]
- Pollock D, Bergman A, Feldman M, Goldstein D (1998) Microsatellite behaviour with range constraints: parameter estimation and improved distances for use in phylogeny reconstruction. Theor Popul Biol 53:256–271 [DOI] [PubMed]
- Rubinsztein DC, Amos W, Leggo J, Goodburn S, Jain S, Li SH, Margolis RL, et al (1995_a_) Microsatellites are generally longer in humans compared to their homologues in non-human primates: evidence for directional evolution at microsatellite loci. Nat Genet 10:337–343 [DOI] [PubMed]
- Rubinsztein DC, Leggo J, Amos W (1995_b_) Microsatellites evolve more rapidly in humans than in chimpanzees. Genomics 30:610–612 [DOI] [PubMed]
- Slatkin M (1995) A measure of population subdivision based on microsatellite allele frequencies. Genetics 139:457–462 [DOI] [PMC free article] [PubMed]
- Sokal RR, Rohlf FJ (1995) Biometry: the principles and practice of statistics in biological research, 3d ed. WH Freeman, New York [Google Scholar]
- Takezaki N, Nei M (1996) Genetic distances and reconstruction of phylogenetic trees from microsatellite DNA. Genetics 144:389–399 [DOI] [PMC free article] [PubMed]
- Weber JL, Wong C (1993) Mutation of human short tandem repeats. Hum Mol Genet 2:1123–1128 [DOI] [PubMed]
- Weiss K (1973) Demographic models for anthropology. Am Antiq 38 (mem 27): 1–186 [Google Scholar]
- Zhivotovsky LA, Feldman MW (1995) Microsatellite variability and genetic distances. Proc Natl Acad Sci USA 92:11549–11552 [DOI] [PMC free article] [PubMed]