Expanding protein universe and its origin from the biological Big Bang (original) (raw)

Abstract

The bottom-up approach to understanding the evolution of organisms is by studying molecular evolution. With the large number of protein structures identified in the past decades, we have discovered peculiar patterns that nature imprints on protein structural space in the course of evolution. In particular, we have discovered that the universe of protein structures is organized hierarchically into a scale-free network. By understanding the cause of these patterns, we attempt to glance at the very origin of life.

It is well known that many proteins with undetectable sequence similarity—as low as expected for random sequences (8–9%)—share a similar three-dimensional structure (fold) (1–4). The possibility that many dissimilar sequences fold into the same stable three-dimensional structure has been demonstrated in a variety of simplified models (5, 6) and is understood on theoretical grounds. General models of protein evolution that are based solely on the requirement of protein stability reproduced observed conservation of amino acids in proteins with dissimilar sequences with reasonable accuracy (4, 7). Several authors have also pointed out that diverse functions can be carried out by proteins of the same fold (8–11). However, a striking observation is that different folds are represented to a different degree in genomes: some folds are represented by many nonhomologous and functionally diverse proteins, whereas other folds are uniquely represented by a single sequence (orphans, i.e., domains that are not structurally similar to any other domains; refs. 12–14). A possible physical or biological reason for such variability in fold representation is one of the major unsolved problems of molecular biophysics.

One suggested explanation of the observed variability in fold representation is based on the premise of convergent evolution. It is presumed that evolution has reached equilibrium in the protein sequence space. Thus, more “designable” folds that can be encoded by many sequences have a higher representation in genomes (15–17). This proposal, called the “designability principle,” is based on phenomenological considerations (18) and on observations drawn from exhaustive enumeration of all sequences in simplified two- and three-dimensional lattice protein models. However, the designability principle has not been successful thus far in predicting the actual structural features of known folds that render them highly designable, in contrast to less populated and orphan folds. Furthermore, the underlying assumption of equilibrium in sequence space is difficult to justify if one considers the sheer size of sequence space.

It is difficult to determine the evolutionary relation between proteins based on their sequence similarity when it is as low as that between randomly selected proteins (8–9%; ref. 4). Given the large number of sequences that correspond to a specific fold (4, 19), structure is a more robust protein characteristic than sequence. To this end, we focus on the analysis and possible genesis of the protein universe based on the structural rather than the sequential classification of proteins. Such analysis may be complicated by the fact that structural similarity is not always rigorously defined. Two popular databases, SCOP (20) and CATH (21), use a semi-intuitive definition of folds that is somewhat subjective. The FSSP database—based on the DALI structure comparison algorithm (2)—defines a quantitative measure of structural similarity, the Z score. However, selection of the threshold value Zmin of the Z score, beyond which proteins are considered structurally similar, also introduces an element of ambiguity into FSSP-based family classification. In a recent paper, Domany and coworkers (22) provided a quantitative relationship between FSSP, CATH, and SCOP classifications. These authors noted that the matrix of pairwise Z scores can be viewed as a weighted graph, where each two proteins that have similarity Z > 2 (Z = 2 is the minimal Z score reported in FSSP) are connected by an edge that carries weight corresponding to the Z score similarity between these two proteins. Clustering algorithms developed for weighted graphs then can be used to identify fold families. However, clustering of weighted graphs is not exact as it may depend on the chosen algorithm and other factors. Another well known problem with structural classification of whole proteins presented in FSSP is so-called “floats,” where two structurally unrelated proteins having a common “promiscuous” domain are identified as structurally similar.

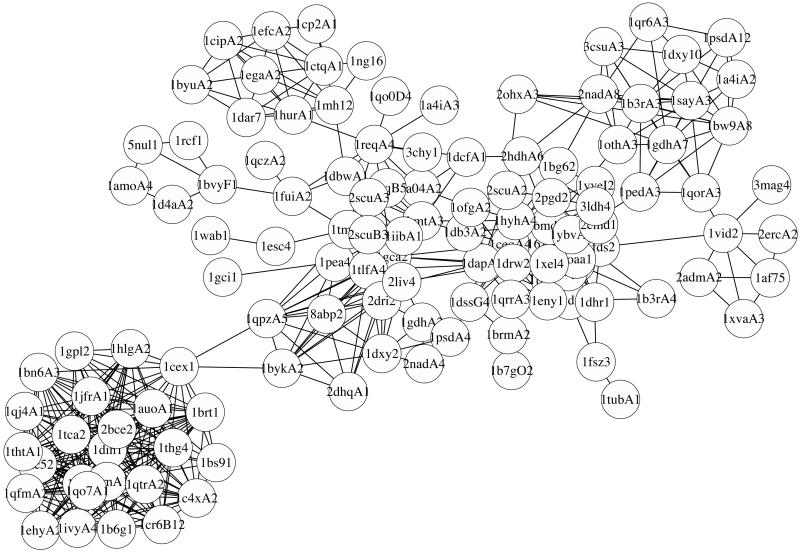
To overcome some of these difficulties, we employ a graph representation of the protein domain universe, in which we consider only protein domains that do not exhibit pairwise sequence similarity in excess of 25%, and each such protein domain represents a node of the graph. We use protein domains as identified by Dietmann and Holm in the FSSP database of protein domains (23). Structural similarity between each pair of protein domains is characterized by their DALI Z score (23). We define a structural similarity threshold Zmin and connect any two domains on our graph that have DALI Z score Z ≥ Zmin by an edge. Thus, we create the protein domain universe graph (PDUG). It is crucial to note that, in contrast to weighted graphs considered in (22), the PDUG is an unweighted graph where each edge that made it above threshold is considered equally. Clustering of such an unweighted graph represents its partitioning into disjoint clusters that can be carried out exactly by using the classical depth-first search algorithm (24). Each disjoint cluster represents a family of structurally related proteins in which each protein is presented only once (Fig. 1). Disjoint PDUG clusters are, in principle, equivalent to the fold classification level of the SCOP database (20).

Fig 1.

Fig 1.

An example of a large cluster of TIM barrel-fold protein domains. Protein domains whose DALI similarity Z score is greater than Zmin = 9 are connected by lines.

Although the fact that PDUG is an unweighted graph significantly simplifies its analysis, such simplification comes at a price of possible dependence of the results on the selection of threshold value Zmin. Thus our first goal is to evaluate how PDUG depends on selection of the threshold value Zmin and whether there is a preferred choice of this parameter. To this end, we study the properties of the largest cluster (giant component; ref. 25) of the PDUG as a function of the cutoff similarity score Zmin. As a key control throughout this work, we compare the properties of the PDUG to that of random graphs that have the same number of nodes and edges as PDUG and the same distribution of pairwise Z scores, but for which the edges are connected randomly. To generate such random graphs, we take the same number of nodes as in PDUG (3,464) and connect randomly chosen pairs by edges. This procedure is repeated until the total number of edges reaches its value (39,479) in the original PDUG (by “original PDUG,” we mean PDUG at the lowest possible threshold Zmin = 2, where all pairs of domains reported by DALI as structurally similar with Z ≥ 2 are connected by an edge). Next, each edge is given a weight, Z score, drawn randomly from a distribution of Z scores for edges observed in a real, original PDUG. Finally, we remove the edges of a random graph with Z < Zmin and identify disjoint clusters by using a depth-first clustering algorithm.

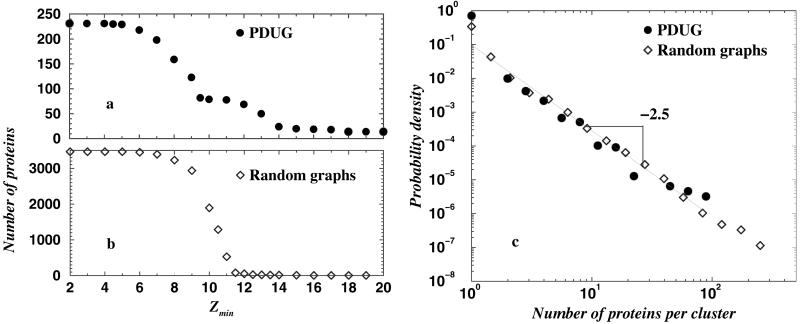
We compute the size of the largest cluster in PDUG and random control graph as a function of Zmin (26). We find a pronounced transition of the size of the largest cluster in PDUG at Zmin = Zc ≈ 9 (Fig. 2a). The random graphs feature a similar transition but at a higher value of Zmin = Zc ≈ 11 (Fig. 2b). The distribution of cluster sizes depends significantly on whether Zmin > Zc or Zmin < Zc for both the PDUG and random graphs. We also find that the probability density, P(M), of cluster sizes M for both the PDUG and random graphs follows a power law at their respective Zc: P(M) ∼ M−2.5 (Fig. 2c). The observed power-law behavior of P(M) is simply a consequence of criticality at Zc as it is featured prominently both for the PDUG and random graphs. The power-law probability density of cluster sizes is a generic percolation phenomenon that has been observed and explained in both percolation (27, 28) and random graph theories (25). Recently, Gerstein and coworkers (29) reported a power-law distribution for fold family sizes derived from the SCOP database and attributed the observed power-law distribution to a certain evolutionary mechanism. However, we find that random graphs feature the same power-law distribution for fold family sizes and are simply explained by percolation theory (25, 27, 28).

Fig 2.

Fig 2.

The dependence of the number of proteins in the maximal cluster on the threshold value of Z score Zmin for PDUG (a) and random graphs (b). (c) The probability density of the cluster sizes for PDUG and random graphs at their respective Zc. Zc indicates the critical value of the Z score threshold at which transition in the size of maximal cluster occurs. For PDUG Zc ≈ 9; for random graphs Zc ≈ 11. We generated 10 different realizations of random graphs, so each point of b represents an average over these 10 realizations. Interestingly, at minimal Zmin = 2, all of the nodes in random graphs are connected; thus, the largest cluster spans all of the protein domains. In contrast, just a small fraction of all nodes (≈250) constitutes the largest cluster in PDUG (at Zmin = 2), pointing to a dramatic difference between PDUG and random graphs. This difference is further revealed in Fig. 3.

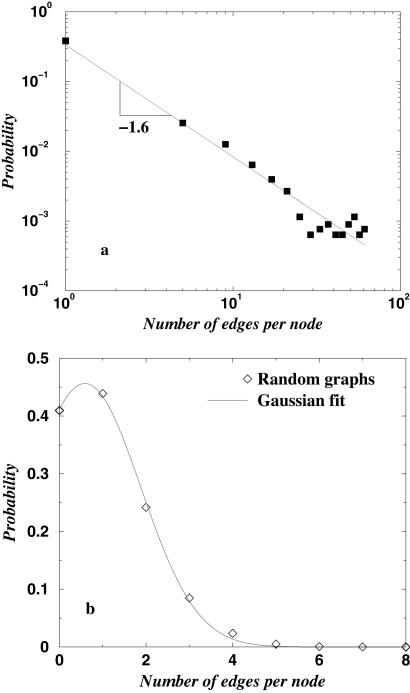
To characterize the structural properties of the PDUG, we compute the probability 𝒫(k) of the number of edges per node k taken at Zmin = Zc for individual clusters. It is known that 𝒫(k) distinguishes random graphs from various graphs observed in science and technology (26). In drastic contrast with the equivalent random graph, the PDUG is scale-free, with 𝒫(k) ∼ _k_−1.6 with a high degree of statistical significance (P < 10−8; Fig. 3_a_). The power-law fit of 𝒫(k) is most accurate at Zmin ≈ Zc and deteriorates noticeably above and below Zc. The fit at Zmin > Zc quickly becomes meaningless as the range of values of connectivity k rapidly diminishes as greater Zmin leads to mostly disconnected domains. At Zmin < Zc, the power-law fit also becomes problematic in the whole range of k because at large values of k (50–100), 𝒫(k) shows some nonmonotonic behavior that can be interpreted as a maximum at large k (the data are insufficient to conclude that with certainty). However, the remarkable property of a maximum 𝒫(k) at k = 0, i.e., dominance of orphans, remains manifest at all Zmin values. This finding is in striking contrast with a random graph which is not scale-free at any value of Zmin (Fig. 3b) and where 𝒫(k) allows almost perfect Gaussian fit with maximum at higher values of k.§

Fig 3.

Fig 3.

The distribution of node connectivity 𝒫(k) for PDUG (a) and for random graph (b) at their corresponding Zc. For PDUG Zc ≈ 9; for random graphs Zc ≈ 11. Node connectivity denotes how many proteins a given protein is connected to by structural similarity connections.

The discovery of the scale-free character of the protein domain universe is striking and represents the main result of this paper. It has immediate evolutionary implications by pointing to a possible origin of all proteins from a single or a few precursor folds—a scenario akin to that of the origin of the universe from the Big Bang. An alternative scenario, whereby protein folds evolved de novo and independently, would have resulted in random PDUG (similar to the one shown in Fig. 3b) rather than that observed in the scale-free one.

The genesis of scale-free networks observed in other areas of science and technology, such as the world wide web, scientific collaboration networks, and domain combinations in proteomes (26, 30–32), has been explained by the peculiar dynamics of their creation. In particular, several dynamic models featuring “preferential” attachment have been proposed (26, 33–35). However, many models predict an exponent α ≥ 2, whereas in our case, α ≈ 1.6.

It is quite suggestive that the origin of the observed scale-free character of the PDUG lies in the evolutionary dynamics of protein fold genesis as a result of divergent evolution from one or a few precursor domains. To this end, we develop a minimalistic model that aims to explain the scale-free PDUG. Specifically, we assume, as do several other models (29, 35), that new proteins evolve as a result of an increase in the gene population primarily by means of duplication with subsequent divergence of sequences by mutations, as well as more dramatic changes such as deletions of certain parts sequences and even possible reshuffling of some structural elements (foldons; refs. 36 and 37).

Our evolutionary dynamics model starts with a single node representing an initial protein. At each time step t, a new protein is generated by means of gene duplication; hence, the total number of proteins created by time step t is exactly t. The creation of a new protein, t + 1, at time step t occurs through gene duplication of some protein k chosen at random (1 ≤ k ≤ t) from the available gene pool generated up to time t. When a protein k is chosen (node Ak), its offspring protein, t + 1, is generated and is represented by node At+1. Importantly, our evolutionary time step is large enough to allow many mutations as well as more dramatic changes in sequences such as insertions/deletions or shuffling of structural elements to occur in the offspring protein such that sequence similarity with the parent protein is lost (4). Such mutations may or may not lead to significant structural divergence of the offspring from its parent protein because the landscape in sequence space is complex (4).

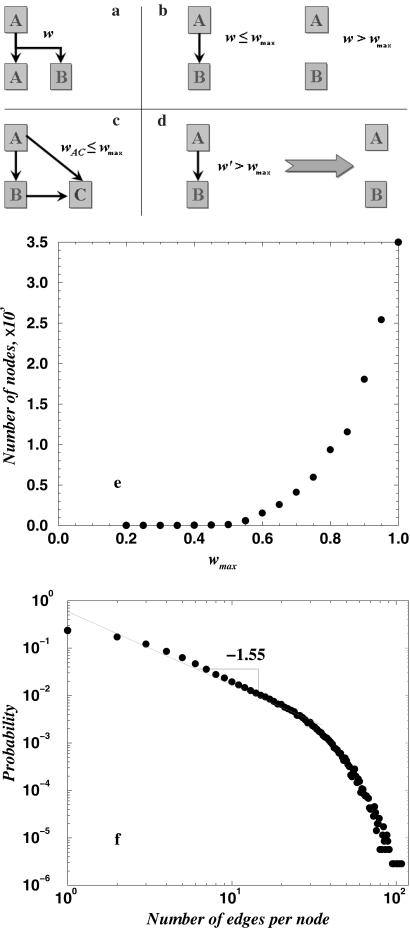
To account for that uncertainty, we assign the distance w between the parent protein and its offspring as a random number uniformly distributed in the interval 0 ≤ w ≤ 1 (Fig. 4a). This quantity may have a conceptual physical meaning of RMSD, an (inverse) Z score, or any other measure of structural similarity between two proteins. If this structural distance is below some critical value _w_max, we assign a bond (edge of the graph) between the newly created node At+1 and its parent node Ak. Otherwise, a new structural family (fold) is created around the protein t + 1, which is an orphan at time t + 1 (Fig. 4b). If the structural divergence between a new protein t + 1 and its parent does not exceed threshold value _w_max, so that an edge between nodes At+1 and Ak is created, we also attempt to connect a newborn At+1 to the set of nodes Ai that are themselves connected by edges to the parent node Ak. The reason for this step is that structural similarity may be transitive; i.e., if a newly born protein t + 1 is similar to its parent k, it might also be similar to other proteins that are themselves similar to k. To evaluate whether structural neighbors of k are similar to its offspring t + 1, we use a simple geometrical ansatz. Because w is a measure of structural divergence, we choose w to satisfy the rule of triangle, where the maximal and minimal sizes of any side of a triangle are determined by the sizes of the second and third sides. In this case, the triangle is formed by the new node At+1, its parent node Ak, and Ai, a structural neighbor of Ak whose distance to At+1 we wish to evaluate. According to the ansatz, we select the distance between Ai to At+1 as a random number, w(At+1, Ai), from the uniform distribution in the interval

Fig 4.

Fig 4.

Proposed model of domain evolution. (a) Gene duplication (A → A + B): the structural similarity between A and B is defined by some function w = (A,B) (e.g., RMSD or DRMSD). (b) If structural similarity w = (A,B) is greater than some critical value w max, then we add a link connecting A and B. If structural similarity is above w max, a new fold family is born. (c) The second generation progeny C (A → B → C) can connect to its grandparent A, if there is structural similarity between A and C: w AC ≤ w max. (d) With each time step, mutations diverge protein structures from each other; i.e., structural similarity changes by some value D: w → _w_′ = w + D(D = 10−4). If _w_′ > w max, we remove the edge between corresponding proteins. (e) The dependence of the size of the largest cluster in the graphs generated by our model on wmax, averaged over 20 realizations. (f) The probability of the node connectivity in our model, averaged over 102 realizations. Apart from the finite-size effects at large k, it exhibits power law distribution with exponent α ≈ 1.6.

|w(At+1,Ak) − w(Ak,Ai)| ≤ w(At+1,Ai) ≤ w(At+1,Ak) + w(Ak,Ai).

If w(At+1,Ai) < wmax, we assign a bond between At+1 and Ai (Fig. 4c).

Additionally, we account for the effects of random mutations and other sequence changes (deletions/insertions) that accumulate over coarse-grained time step t and lead to structural divergence in the protein universe (like the expanding universe in astronomy). To this end, at each time step we increase the structural distances w between all proteins by a small number D: wij → w_′_ij = wij + D (Fig. 4d). If the new weight w_′_ij exceeds wmax, we remove a bond between Ai and Aj.

We perform simulations for 3,500 maximal nodes and average over 20 runs to compute the dependence of the largest cluster size (giant component) in the generated graphs on wmax and find that there is a transition at wmax ≈ 0.75 (Fig. 4e). Hence, wmax ≈ 0.75 corresponds to a critical region in this model, analogous to Z_c_ ≈ 9 for the PDUG. Indeed, we find (Fig. 4f) that the probability 𝒫(k) of node connectivity follows a power-law up to finite-size effects at large k, and that the power-law exponent is ≈ 1.6, close to that in the PDUG. Importantly, the results presented in Fig. 4f are averaged over 102 realizations of generated networks, although each individual realization yields a similar distribution, albeit a noisier one, so that for an individual realization, the power-law estimate belongs to an interval between 1.4 and 1.9. The presented model, being coarse-grained, does not aim at a detailed and specific description of protein evolution. However, it illustrates that divergent evolution is a likely scenario that leads to scale-free PDUG.

Our method of clustering protein structures provides a number of insights. First of all, using graph theory for protein structure classification removes the ambiguities that are inherent in the highly useful, albeit manual, approaches to structural classification of proteins (20, 21). Perhaps not surprisingly, we observed that the structure of the graph representing the protein domain universe depends on the Zmin threshold value of Z score, above which protein domains are considered structurally similar and are connected by an edge of the graph. However, at a certain critical value, Zmin = Zc, the structure of the PDUG becomes remarkably universal, simple, and amenable to theoretical understanding from an evolutionary standpoint.

An important component of our analysis is random control where PDUG is compared with random graph. Our results show that random weighted graph having the same weight (Z score) distribution as PDUG features the same cluster-size distribution. Because clusters in PDUG can be associated with fold-level classification of protein structure, this observation suggests that nonuniform distribution of nonhomologous proteins over folds may not be due to special features of “most popular” protein folds, as suggested by some researchers (17, 18). However, that does not necessarily imply that observed protein folds are not selected based on their physical properties (8). It may well be that the divergent evolution scenario described here occurs only on these selected folds, whereas unfeasible ones are not observed in nature. However, our analysis points out that an explanation of the nonuniform distribution of nonhomologous proteins over observed folds does not require one to invoke a designability principle (17) or related conjectures about the nonuniform density of sequences in the space of protein folds (18).

We discovered that the structure of the PDUG is, by far, nonrandom, but rather represents a scale-free network featuring the power-law distribution of number of edges per node. The most striking qualitative aspect of the observed distribution is the much greater number of orphans compared with random graph control. Importantly, this qualitative feature remains prominent at any value of threshold Zmin, despite the fact that power-law fits of 𝒫(k) get worse when Zmin deviates from Zc. A natural explanation of this finding is from a divergent evolution perspective. The model of divergent evolution presented here is in qualitative agreement with PDUG, as it produces large (compared with random graph) number of orphans at all values of wmax. Orphans are created in the model mostly through gene duplication and their subsequent divergence from precursor. This conjecture may be meaningful biologically, because duplicated genes may be under less pressure and, hence, prone to structural and functional divergence. The divergent evolution model presented here is a schematic one, as it does not consider many structural and functional details, and its assumptions about the geometry of protein domain space in which structural diffusion of proteins occurs may be simplistic. However, its success in explaining qualitative and quantitative features of PDUG supports the view that all proteins might have evolved from a few precursors.

Finally, we want to comment on the robustness of our results. Indeed, power-law scaling of 𝒫(k) is observed only in a range of threshold values Zmin; special algorithms were applied to discern such behavior. Does nature use similar algorithms and select similar thresholds? In our opinion, nature is not concerned at all with power-laws and with algorithms in their generation. We believe that creation of functionally (and as a consequence of it, structurally) diverse proteins could have been one of the driving forces of evolution. Our motivation in this work is to “spy” on nature by using algorithms as devices to see implications of evolutionary processes in existing proteins. Selection of a particular value of threshold Zmin means just a choice of conditions at which these spying devices are most effective in discerning natural events from random ones.

Acknowledgments

We thank A. G. Murzin, L. Holm, and B. Dominy for helpful discussions. We are especially grateful to L. Mirny for his advice on the project and to E. Deeds for his help. We thank N. Grishin, A. Grosberg, and A. Finkelstein for their reading of the manuscript and their useful critical comments. This work is supported by National Institutes of Health Grant GM52126 (to E.I.S.) and National Institutes of Health National Research Service Award Fellowship GM20251 (to N.V.D.).

Abbreviations

§

Because of the small number of domains with >25% pairwise sequence similarity, we included all domains in PDUG. We also tested whether this small number of homologous domains affected our 𝒫(k); we found that if we discard one of these homologs, the resulting 𝒫(k) does not change significantly.

References