Molecules in motion: influences of diffusion on metabolic structure and function in skeletal muscle (original) (raw)
Abstract
Metabolic processes are often represented as a group of metabolites that interact through enzymatic reactions, thus forming a network of linked biochemical pathways. Implicit in this view is that diffusion of metabolites to and from enzymes is very fast compared with reaction rates, and metabolic fluxes are therefore almost exclusively dictated by catalytic properties. However, diffusion may exert greater control over the rates of reactions through: (1) an increase in reaction rates; (2) an increase in diffusion distances; or (3) a decrease in the relevant diffusion coefficients. It is therefore not surprising that skeletal muscle fibers have long been the focus of reaction–diffusion analyses because they have high and variable rates of ATP turnover, long diffusion distances, and hindered metabolite diffusion due to an abundance of intracellular barriers. Examination of the diversity of skeletal muscle fiber designs found in animals provides insights into the role that diffusion plays in governing both rates of metabolic fluxes and cellular organization. Experimental measurements of metabolic fluxes, diffusion distances and diffusion coefficients, coupled with reaction–diffusion mathematical models in a range of muscle types has started to reveal some general principles guiding muscle structure and metabolic function. Foremost among these is that metabolic processes in muscles do, in fact, appear to be largely reaction controlled and are not greatly limited by diffusion. However, the influence of diffusion is apparent in patterns of fiber growth and metabolic organization that appear to result from selective pressure to maintain reaction control of metabolism in muscle.
Keywords: calcium, diffusion, metabolism, mitochondria, muscle, nuclei
Introduction
Physiologists have a long history of evaluating the role of diffusion in cellular metabolism, particularly with respect to the necessity for O2 transport from the blood into cells for aerobic metabolism. Indeed, Fick's diffusion equations and principles of membrane transport have a prominent position in most physiology textbooks, and biology students are well versed in the notion that cells are small in order to maintain short diffusion distances for molecules like O2. A corollary of this rule in skeletal muscle is that aerobic fibers that rely on O2 diffusion to promote sustained exercise are generally smaller than anaerobic fibers that are used for burst contraction and are less reliant on O2 diffusion (for review, see van Wessel et al., 2010). The implication of this observation is that higher rates of aerobic metabolism require smaller fibers, and variation in fiber size may represent responses to avoid diffusion limitation. In a more general sense, we can conclude that in any reaction–diffusion system, the role of diffusion becomes greater as the diffusion coefficient (D) decreases, diffusion distance increases or the rate of reaction flux increases (Weisz, 1973).
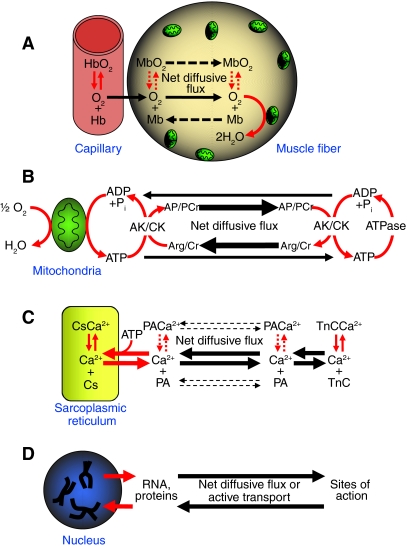
In principle, nearly every biochemical reaction is a reaction–diffusion process involving the diffusive flux of substrates to enzyme active sites. A number of processes have been the subject of reaction–diffusion analyses in muscle, such as the aforementioned oxygen flux from capillaries to mitochondria (Fig. 1A), the diffusion of ATP to sites of cellular ATPases (Fig. 1B), Ca2+ cycling during contraction–relaxation cycles (Fig. 1C), and the transport of nuclear products to sites of action in the cell (Fig. 1D). These examples illustrate considerable variation in D values, diffusion distances and rates of reaction fluxes. For instance, Ca2+ cycling entails a high D for Ca2+, short diffusion distances and high reaction fluxes, whereas nuclear function entails low D values for various macromolecular products, long diffusion distances and low reaction fluxes. These interactions mean that cell structure is responsive to diffusion constraints in a manner that is dependent on the type of process and the functional demands placed on that process. Fig. 1 also illustrates the principle of facilitated diffusion that was first proposed for myoglobin (Mb) by Wittenberg (Wittenberg, 1959) and independently identified for hemoglobin (Hb) by Scholander (Scholander, 1960), but also applies to phosphagen kinases such as creatine kinase (CK) and arginine kinase (AK), and to a lesser extent to parvalbumin (PA). In facilitated diffusion, protein binding or enzymatic conversion of the diffusing species provides a parallel pathway for diffusive flux that enhances the overall rate of diffusive transport. The present paper will attempt to summarize some of the ways in which diffusion governs metabolic structure and function in skeletal muscle.
Fig. 1.
Examples of reaction–diffusion processes in muscle. (A) O2 diffusion entails reversible binding with hemoglobin (Hb) or another blood pigment type, and with myoglobin (Mb) in some fiber types. (B) Diffusion of ATP to cellular ATPases involves the reversible transfer of a phosphoryl group from ATP to an acceptor molecule such as creatine (Cr) or arginine (Arg), forming the phosphagen phosphocreatine (PCr) or arginine phosphate (AP), respectively. Phosphagen kinases, such as creatine kinase (CK) or arginine kinase (AK) catalyze these reactions. (C) Ca2+ is released from the sarcoplasmic reticulum (SR) upon muscle stimulation and must diffuse to and bind myofibrillar troponin C (TnC) to activate contraction. Relaxation entails the uptake of Ca2+ into the SR, where reversible binding to calsequestrin (Cs) may occur. In some fiber types, parvalbumin (PA) reversibly binds Ca2+ that is in the sarcoplasm. In addition, ATP binds Ca2+ and may further facilitate diffusion (not shown). (D) Transcription and translation entails diffusive flux of nuclear products to various sites of action in the cell. In all cases, the red arrows indicate protein-mediated binding, transport or catalysis, while the black arrows indicate diffusion. The thickness of the arrows indicates the relative importance of the diffusive pathway. Dashed lines indicate that Mb and PA are not present in all fiber types.
Concentration gradients are a prerequisite for diffusion control of reaction flux
When examining a single tissue type, D is comparatively invariant over physiological time scales, so the extent to which diffusion influences cell structure and function is largely governed by the interaction between diffusion distance and reaction flux rate. In skeletal muscle fibers rates of reaction fluxes and diffusion distances can vary over several orders of magnitude. For instance, aerobic metabolic rate in white muscle from fishes and crustaceans can be <0.1 μmol ATP g–1 min–1 (Kinsey et al., 2005; Nyack et al., 2007), whereas in insect flight muscle it can exceed 2000 μmol ATP g–1 min–1 (Suarez, 1998). Similarly, diffusion distances within fibers can vary from <1 μm to several hundred micrometers (Kinsey et al., 2007). At issue is whether an intracellular process leads to the formation of concentration gradients. Most efforts to model metabolism in muscle have focused exclusively on kinetic properties, and these approaches have successfully predicted metabolic fluxes over a range of physiological states (e.g. Vicini and Kushmerick, 2000; Lambeth and Kushmerick, 2002; Korzeniewski, 2003; Beard, 2005). An underlying assumption of these approaches is that diffusion is rapid relative to the rate of metabolic flux, and it therefore does not limit reactions.
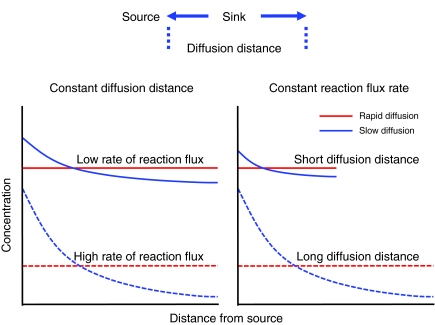
Fig. 2 is a diagram of the manner in which diffusion distance and reaction flux interact to affect concentration profiles of a diffusing molecule for cases where diffusion would not be limiting and for cases where it may be limiting. In this example, there is a point source for the diffusing molecule and that molecule is consumed (sink) as it diffuses away from the source. For instance, the source could be a capillary supplying O2 that diffuses across the cell and is consumed by mitochondria. The schematic diagram in Fig. 2 illustrates that in cases where diffusion is fast relative to the reaction rate, there are no concentration gradients for the diffusing species (red lines). This represents a situation where diffusion would have no effect on reaction rate, and an analysis of the catalytic properties alone is sufficient to explain the metabolic process. Thus, an increase in the reaction rate or the diffusion distance (manifested here as increased activity or size, respectively, of the sink) would lead to a uniform reduction in the concentration of the diffusing species over the diffusion distance. The blue lines illustrate what would be expected when diffusion is not much faster than the rate of reaction flux, leading to concentration gradients that become steeper as the reaction rate or the diffusion distance increases. In these cases, if the diffusing species is a substrate for a reaction, then the rate of product formation may be reduced as the distance from the source increases.
Fig. 2.
Schematic diagram of the interaction between diffusion distance and reaction flux rate in concentration profiles for cases where diffusion is very rapid compared with the flux rate (red lines) and cases where diffusion is not much more rapid than the flux rate (blue lines). The red lines therefore represent cases where diffusion can be ignored and catalytic properties exert complete control over reaction flux. Cases with higher rates of reaction flux or longer diffusion distances are indicated by dashed lines. The left panel shows the influence of changes in the reaction flux when diffusion distance is constant and reaction flux varies, and the right panel shows the influence of diffusion distance when the reaction flux is constant and diffusion distance varies. See text for additional details.
Unfortunately, measurements of metabolite concentrations in cells typically cannot distinguish between the rapid diffusion and slow diffusion cases, as they do not give information on spatial variation in concentration. Most studies have therefore analyzed reaction–diffusion processes in muscle using mathematical models that include independent measurements of D, diffusion distances and rates of reaction fluxes. This requires a clear understanding of the nature of the intracellular environment and the manner in which small and large molecules move in this environment.
The intracellular environment of muscle has characteristics of a porous medium
The cytoplasm is a complex and crowded medium consisting of soluble and bound macromolecules, fibrous cytoskeletal elements and membrane-bound organelles (reviewed in Luby-Phelps, 2000; Saks et al., 2008). Skeletal muscle has a highly regular and ordered intracellular environment where most of the volume is devoted to the myofibrils, sarcoplasmic reticulum (SR) and mitochondria. Wheatley and colleagues have argued that classical diffusion theory should not be applied to intracellular movement because (1) many of its assumptions may be violated in the cytoplasm, (2) much of intracellular transport is ‘directed’ rather than random, and (3) the cytoplasmic structure is incompletely characterized and temporally dynamic, and our understanding of interactions of mobile species within this internal structure is inadequate to permit mathematical evaluation (Agutter et al., 1995; Wheatley, 2003). These concerns appear to be greatest for macromolecules that may be present in relatively low concentrations, actively transported along cytoskeletal elements in some cell types, and subject to specific binding interactions. While we appreciate these points, we would argue that the experimental evidence, some of which is summarized here, indicates that much of molecular motion in muscle fibers is true diffusion that can be evaluated mathematically, as is common practice in engineering literature when describing molecular movement in porous media such as gels (reviewed in Locke, 2001). This is particularly true for large, anaerobic fibers from organisms such as fishes and crustaceans, where, for example, the few mitochondria in the fiber produce ATP that must move long distances through the myofibrillar lattice (discussed below). There is no evidence for metabolic compartmentalization (as has been proposed for mammalian cardiomyocytes) (see Saks et al., 2008) or targeted transport in this type of cell, and diffusion seems the most likely mechanism for equilibrating ATP in the fiber. Thus, in this paper we will use the term ‘diffusion’, which can be characterized by D, where it seems to apply based on the experimental data.
Methods of measurement of intracellular diffusion in muscle are largely dependent on the type of molecule being observed. Diffusion of gases through tissues has been the subject of study for nearly 100 years, and typically entails measurement of partial pressures on either side of a tissue through which diffusion is occurring. Diffusion of small metabolites and ions in muscle has been measured using isotopic labeling (Kushmerick and Podolsky, 1969) and reversibly binding fluorophores (Bernengo et al., 2001), but the majority of studies in muscle have used pulsed-field gradient nuclear magnetic resonance (NMR) or diffusion-sensitive magnetic resonance imaging (MRI) (reviewed in Nicolay et al., 2001). Diffusion of macromolecules such as proteins is difficult to measure using NMR because the relatively slow rotational motion of these molecules causes severe broadening of spectral peaks, although myoglobin diffusion in muscle has been measured using this approach (Livingston et al., 1983; Lin et al., 2007). Therefore, fluorescent-labeling approaches, principally fluorescence recovery after photobleaching (FRAP) techniques, have been the mostly widely used means of measuring macromolecular diffusion in muscle (reviewed in Verkman, 2003).
Bunch and Kallsen measured diffusion of water, urea and glycerol in barnacle muscle fibers and found, surprisingly, that there were no differences between D in the muscle sarcoplasm and in an aqueous solution (Bunch and Kallsen, 1969). Kushmerick and Podolsky, in contrast, found that a variety of ionic and non-ionic species of low molecular mass had D values for diffusion along the length of frog muscle fibers that were reduced by approximately 50% from those seen in aqueous solution (Kushmerick and Podolsky, 1969). This difference was attributed to intracellular structures that hinder diffusion and the relatively high protein concentration in cells, and similar results have since been found for a range of metabolites and fiber types. For instance, intracellular D values of small metabolites like phosphagens, ATP, lactate and alanine have been found to be approximately 2-fold lower than in aqueous solution in isolated muscle from frog (Yoshizaki et al., 1982), fish (Hubley et al., 1995; Hubley and Moerland, 1995; Kinsey et al., 1999) and crustaceans (Kinsey and Ellington, 1996; Kinsey and Moerland, 2002). Similar results have been seen in mammalian skeletal muscle in vivo (Moonen et al., 1990; van Gelderen et al., 1994; de Graaf et al., 2000; de Graaf et al., 2001). Soluble proteins increase the viscosity of solutions like the cytoplasm, and the ordering of water on hydrophobic surfaces or in hydration shells around charged intracellular components might also reduce mobility in the cytoplasm. Both of these effects might be expected to lead to the observed reduction in the intracellular D of metabolites compared with that in aqueous solution. However, careful measurements have shown that while the shear viscosity of the cytoplasm may be relatively high (making it more resistant to flow than bulk water), the intracellular solvent viscosity is low and similar to that of bulk water (Fushimi and Verkman, 1991; Luby-Phelps et al., 1993). This suggests that the reduced D of metabolites inside muscle fibers is the result of intracellular structures that hinder motion (including soluble proteins) rather than the inherent viscous properties of intracellular water.
Diffusion of macromolecules in muscle is also reduced compared with that in aqueous solution, but to a much greater extent than in small molecules. The diffusion of Mb in skeletal muscle has been of particular interest because of its role in reversibly binding O2 and therefore serving as a temporary O2 store and facilitating O2 diffusion (reviewed in Wittenberg and Wittenberg, 2003). Several studies have found that D of Mb in muscle fibers is about 1/6 to 1/10 of that in aqueous solution (Baylor and Pape, 1988; Jurgens et al., 1994; Papadopoulos et al., 1995; Papadopoulos et al., 2000; Papadopoulos et al., 2001). Measurements of protein diffusion in skeletal muscle from frog (Maughan and Lord, 1988; Maughan and Godt, 1999) and cultured mammalian fibers (Arrio-Dupont et al., 1997; Arrio-Dupont et al., 2000) yielded D values that were minimally 1/3 lower than that in water, and in many cases much more dramatically reduced. Analyses of the influence of hydrodynamic radius on the D values of macromolecules demonstrated that for both proteins (Papadopoulos et al., 2000; Arrio-Dupont et al., 2000) and dextrans (Arrio-Dupont et al., 1996) the difference between D in the sarcoplasm and D in water increased with molecule size, until in the largest proteins D was essentially negligible. This indicates that diffusion of large molecules in muscle is more hindered by intracellular structures such as the myofilaments than are small metabolites, and macromolecules or large complexes like polysomes exceeding 10–20 nm in radius may be nearly immobile (Russell and Dix, 1992; Arrio-Dupont et al., 2000; Papadopolous et al., 2000).
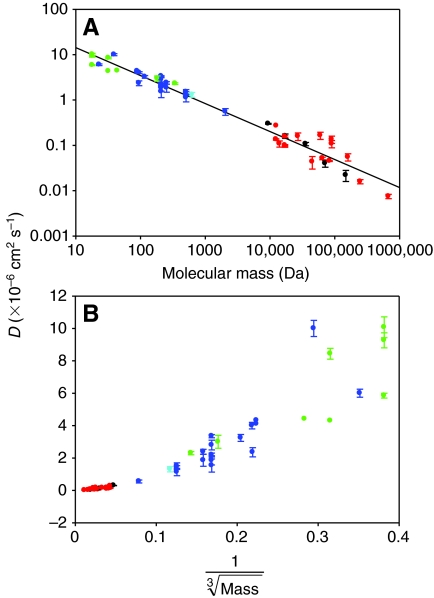
The effect of hydrodynamic radius on globular proteins is more dramatic than in dextrans, which are thought to have a random coil structure that allows them to more readily access the diffusible volume of the fiber (Arrio-Dupont et al., 2000). Nevertheless, D in muscle fibers is ultimately inversely related to molecular mass for a wide range of molecules, despite the variation in the way intracellular structures interact with molecules that differ in size and conformation (Fig. 3A) (Papadopolous et al., 2000). However, as observed by Arrio-Dupont and colleagues (Arrio-Dupont et al., 1996) for dextran diffusion, D is linearly related to the inverse of the square root of molecular mass (not shown), rather than the cube root as would be expected from the Stokes–Einstein relationship (Fig. 3B). Arrio-Dupont and colleagues attributed this discrepancy to the fact that the Stokes–Einstein relationship describes diffusion of a hard sphere, whereas real molecules are not spherical or necessarily compact (Arrio-Dupont et al., 1996), but we might also conclude that increased steric effects in macromolecules might further alter the relationship between D and molecular mass in muscle when evaluated over a large size range of molecules.
Fig. 3.
Relationship between the diffusion coefficient (D) in muscle and molecular mass for a diversity of skeletal muscle and molecule types. D values have been corrected to a temperature (T) of 20°C using a _Q_10 for diffusion in muscle of 1.28 (Hubley et al., 1995). Only freely diffusing species are plotted here. Molecules that are bound or compartmentalized in the fiber (e.g. Ca2+) or those macromolecules or complexes (e.g. polysomes) that are too large to move through the fiber have lower D values than would be predicted from molecular mass (not shown). Green: small, uncharged molecules; blue: ions or small charged metabolites; red: proteins; black: dextrans; cyan: the small, fluorescent probe calcein-AM. See text for additional details. Regression line: _D_=87.09×molecular mass–0.69, _R_2=0.86, P<0.0001. Data are means ± s.e.m. D values were obtained from the studies discussed in the text.
It should be noted that we have not included in Fig. 3 diffusing species that are known to be bound or compartmentalized in the fiber, such as Ca2+, or those macromolecules that are so large as to be essentially immobile, because these conditions lead to a much reduced apparent D (Kushmerick and Podolsky, 1969; Arrio-Dupont et al., 2000; Papadopolous et al., 2000). This is not an effort to deemphasize the importance of specific or non-specific binding, enzyme localization or potential compartmentalization. Rather, we are summarizing the movement of intracellular molecules and other probes where D has been measured without these confounding effects, in order to evaluate the nature of the intrafiber environment. In addition, it is possible that intracellular convection associated with contraction may enhance intracellular transport (Hochachka, 1999; Suarez et al., 2003). There has been limited experimental testing of this hypothesis, although the D of several proteins was not increased by muscle contraction or passive stretching and shortening (Baylor and Pape, 1988; Papadopoulos et al., 2000). To our knowledge the influence of contraction on the diffusion of small metabolites has not been addressed, and further study in this area is warranted.
Diffusion in muscle is orientation dependent (for small molecules)
One of the hallmarks of muscle intracellular structure is that it is highly orientation dependent (anisotropic), most notably with respect to the myofilaments that are aligned with the long axis of the cylindrical fibers. It is therefore not surprising that diffusion in various skeletal muscle types is also anisotropic, where radial diffusion is slower than axial diffusion for small molecules like water (Cleveland et al., 1976; Galban et al., 2004), phosphocreatine (Pcr) (Moonen et al., 1990; van Gelderen et al., 1994; Kinsey et al., 1999; de Graaf et al., 2000), ATP (de Graaf et al., 2000), arginine phosphate (Kinsey and Moerland, 2002) and the fluorescent probe calcein (Hardy et al., 2009), as well as for some larger molecules like mRNAs (Dix and Eisenberg, 1988). The reduction in the radial D is time dependent, where D declines with increasing diffusion time until 100–200 ms, at which point D reaches a steady-state value (Moonen et al., 1990; van Gelderen et al., 1994; Kinsey et al., 1999; de Graaf et al., 2000; Kinsey and Moerland, 2002). In contrast, axial D is generally independent of diffusion time. This pattern is again characteristic of diffusion through a porous medium, where as the diffusion time increases the diffusing species is more likely to encounter a barrier that will impede its progress, thus lowering D. A steady-state D is reached when the distance traveled greatly exceeds the spatial scale of the barriers.
It has been difficult to account for the barriers that induce the pattern of diffusion observed in muscle. It has been proposed that restriction within the cylindrical sarcolemma is responsible for the time-dependent anisotropy of D in muscle (Moonen et al., 1990; van Gelderen et al., 1994). However, the same anisotropic pattern was observed in isolated fish and crustacean muscles that had very large diameters, and simulations of diffusion within cylinders of this size indicated that the sarcolemma had a negligible influence on the observed pattern of diffusion (Kinsey et al., 1999; Kinsey and Moerland, 2002). These studies also included models of diffusion through the thick and thin filament lattice, and showed that the nanometer scale of these diffusion barriers caused a time-dependent decrease in D that was much too fast to account for the observed pattern. Based on the evidence that spatial barriers intermediate in scale to the thick and thin filament array (nanometer scale) and the sarcolemma (tens or hundreds of micrometers in scale), the SR was proposed as a likely intracellular barrier that could explain the observed pattern of anisotropy (Kinsey et al., 1999; Kinsey and Moerland, 2002).
Using a different mathematical approach and assuming a cylindrical barrier to diffusion in the muscle fiber, de Graaf and colleagues proposed that intracellular barriers with a length scale of 16–22 μm accounted for the pattern of diffusion in muscle (de Graaf et al., 2000), but the identity of such a barrier is unknown (SR spacing is typically 1–3 μm). Similar results were obtained from the mathematical analysis of Aliev and Tikhonov, who found that a semi-permeable SR membrane shield could explain the experimental measurements of diffusion anisotropy, but only if the diameter of the shield was about 20 μm (Aliev and Tikhonov, 2004). More recently, Shorten and Sneyd found that they could predict the observed diffusion anisotropy by modeling the influence of thick and thin filaments, SR, t-tubules and mitochondria, suggesting no role for increased cytoplasmic viscosity on D (Shorten and Sneyd, 2009), which is consistent with data indicating that the solvent viscosity of the cytoplasm is not substantially different from water (see above). However, their analysis only characterized the steady-state pattern of diffusion and not the time dependence of D, so the intracellular structure(s) leading to the observed anisotropy pattern in a variety of skeletal muscle types remains to be identified.
While the pattern of anisotropic diffusion of small metabolites has been observed consistently, diffusion of proteins appears to be isotropic (Maughan and Godt, 1999; Papadopoulos et al., 2000; Lin et al., 2007). Shorten and Sneyd provided two potential explanations for the discrepancy between small and large molecules (Shorten and Sneyd, 2009). First, barriers to axial movement, such as the _Z_-line and _M_-line, might serve to obstruct diffusion of large molecules, while smaller molecules presumably pass through more easily. Second, hydrodynamic wall effects become important for large molecules diffusing in confined spaces. Interactions of macromolecules with intracellular structures can impede progress even if the structure surface is oriented parallel to the direction of diffusion, and this hydrodynamic drag will increase as the diffusing species approaches the size of the pores in the media. Thus, diffusion will become more isotropic as hydrodynamic radius increases (Shorten and Sneyd, 2009).
Evaluating diffusion-dependent processes in muscle
Aerobic metabolism
Measurements of D in muscle as described above, along with microscopic analyses of diffusion distances and measurements of the rates of metabolic processes, have been used to quantitatively evaluate the reaction–diffusion processes in skeletal muscle shown in Fig. 1. By far, the most widely studied is aerobic metabolism, which depends on the diffusion of O2 to the mitochondria and the subsequent diffusion of ATP to sites of utilization in the fiber (Fig. 1A,B). A comprehensive review of the literature on the role of diffusion in aerobic metabolism is beyond the scope of this paper, so we will briefly focus on a few examples and some of the general conclusions.
The pioneering work of August Krogh and A. V. Hill provided equations that are still used to describe concentration profiles of O2 (Krogh, 1919) and high-energy phosphate molecules (Hill, 1965) in muscle. Mainwood and Rakusan (Mainwood and Rakusan, 1982) applied these equations to show that clustering of mitochondria near capillaries and the presence of a near-equilibrium CK reaction led to a smaller decrease in P_O2 across the cell and less steep gradients for PCr, ATP and ADP, and therefore helped preserve the free energy of ATP hydrolysis, Δ_G, across the fiber. This provided the first quantitative demonstration that the distribution of mitochondria in skeletal muscle is influenced by diffusion constraints (see below). A number of more elaborate mathematical models of O2 flux and metabolism have been developed for skeletal muscle (e.g. Federspiel, 1986; Groebe, 1995; Hoofd and Egginton, 1997; Piiper, 2000; Lai et al., 2007; Dash et al., 2008), and there are a number of reviews of aspects of O2 and aerobic substrate transport to mitochondria in muscle (e.g. Hoppeler and Weibel, 1998; Wagner, 2000; Suarez, 2003; Weibel and Hoppeler, 2004). Some conclusions from past work are that (1) control of O2 flux to, and usage by, mitochondria is shared among the various steps in the O2 cascade, (2) a substantial decrease in _P_O2 occurs between the capillary and the fiber, and (3) intracellular O2 gradients may be present. Thus, the rate of O2 diffusion into and across the fiber to the mitochondria may influence muscle structure and function. The intracellular O2 concentration gradients that are necessary for diffusion control of aerobic metabolism are notoriously difficult to demonstrate experimentally. However, spatial gradients in the redox state of isolated frog skeletal muscle fibers suggest that O2 gradients may influence rates of oxidative phosphorylation even under conditions of high extracellular _P_O2 (Hogan et al., 2005). Further, measurements of O2 consumption rates and force production in isolated frog skeletal muscle fibers and rat myocardial trabeculae suggest that maximal respiration rates cannot be attained in vivo because O2 diffusive flux is insufficient to prevent anoxia in the fiber core (van der Laarse et al., 2005).
The wide interest in intracellular O2 transport has prompted many studies of Mb, as it is the final mediator of O2 flux to the mitochondria. Mb is a small intracellular oxygen-binding heme protein that is found in aerobic fibers, and is thought to function primarily in temporal buffering of _P_O2 and in facilitated transport of O2 to mitochondria (reviewed in Conley et al., 2000; Jurgens et al., 2000; Wittenberg and Wittenberg, 2003; Ordway and Garry, 2004). While its role as a temporal buffer is generally accepted, the importance of the related facilitated diffusion function has been questioned based on reaction–diffusion analyses that incorporated the relatively low D for Mb in muscle fibers (e.g. Jurgens et al., 2000; Lin et al., 2007). However, Mb-facilitated diffusion becomes more important in skeletal muscle at low _P_O2 (Lin et al., 2007). Compensatory responses in the cardiovascular system that enhance O2 delivery in Mb knock-out mice first reported by Gödecke and colleagues seem to support an O2 transport role for Mb (Gödecke et al., 1999). However, Mb also has nitric oxide (NO) oxygenase activity (Flögel et al., 2001), and it has been proposed that the ‘naturally occurring genetic knockout’ of Mb and Hb in Antarctic icefishes leads to cardiovascular compensations that stem from high levels of NO, rather than from reduced O2 delivery per se (Sidell and O'Brien, 2006). Thus, while a facilitated diffusion function is an unavoidable consequence of the free diffusion of Mb and rapid reversible binding to O2, the relative importance of this transport role remains the source of debate.
The diffusion of ATP from the mitochondria to cellular ATPases has also been a subject of contention. Bessman and Geiger (Bessman and Geiger, 1981) originally proposed the ‘PCr shuttle’ to explain ATP delivery from the mitochondria to cellular ATPases (Fig. 1B), where the bulk of ATP-equivalent transport occurred via PCr diffusion, rather than directly as ATP. Central tenets of this idea as it has evolved are that the mitochondrial outer membrane is a barrier for ATP/ADP diffusion, but not for PCr/Cr diffusion (although this notion has been disputed) (see Kongas et al., 2004), and that ATP produced in the mitochondria passes directly from the adenine nucleotide translocator in the inner membrane to the mitochondrial form of CK. Meyer and colleagues provided an opposing view using a simple facilitated diffusion model (akin to that used to assess Mb function) to evaluate ATP-equivalent diffusive flux (Meyer et al., 1984) and concluded that (1) most ATP-equivalent diffusion should occur in the form of PCr because of its higher concentration and higher D, and (2) there are minimal concentration gradients of high energy phosphates in muscle. There has been a great deal of experimental and modeling work since these early studies that has characterized so-called phosphotransfer networks like the CK system with respect to enzyme localization, channeling of substrates, and restricted diffusion in mammalian skeletal and cardiac muscle, and a number of contrasting reviews are available (e.g. Walliman et al., 1992; Dzeja and Terzic, 2003; Saks et al., 2008; Beard and Kushmerick, 2009). While the function of the CK system is largely viewed through the lens of the mammalian cardiomyocyte, Ellington provides a review of the evolution and function of the entire family of phosphagen kinases that are found in animals (Ellington, 2001).
The role of diffusion in responses of fish muscle aerobic metabolism to cold has been the focus of study because both catalytic and diffusive processes are slower at lower temperature. Muscle from cold-acclimated or -adapted fishes typically has a high mitochondrial volume density and high lipid composition, compared with that in warm water species. The high mitochondrial content is thought to not only offset the reduced reaction rates at colder temperatures but also shorten diffusion distances between mitochondria (e.g. Johnston, 1982; Egginton and Sidell, 1989) (reviewed in Sidell, 1998). Hubley and colleagues used a reaction–diffusion model of high-energy phosphates to evaluate metabolism as a function of temperature in red and white goldfish muscle, and concluded that diffusion constraints of these molecules were not the primary cause of mitochondrial proliferation in the cold (Hubley et al., 1997). However, the higher lipid content in cold water fishes, including the lipid membranes in the abundant mitochondria, likely aid diffusion of O2 because of its higher solubility in lipids than in the aqueous cytosol (Sidell, 1998). Further, the mitochondria in hemoglobin-free icefishes are larger, have a higher lipid:protein ratio, and do not have a higher catalytic capacity than in warm water species, indicating that mitochondrial volume increases may serve to promote O2 diffusion in this group rather than to maintain catalytic capacity in the cold (O'Brien and Mueller, 2010). Egginton and colleagues used a reaction–diffusion model to evaluate O2 gradients in aerobic muscle from Antarctic, sub-Antarctic and Mediterranean species of fishes (Egginton et al., 2002). Temperature had a large influence on the extent of gradients as expected, but the _P_O2 in the core of the fiber was inversely related to fiber size across species and temperature regimes, indicating that diffusion distance is a critical parameter constraining aerobic design in some fish muscle.
Ca2+ cycling
Muscle contraction entails the release of Ca2+ from the terminal cisternae during muscle activation and diffusion of Ca2+ to troponin C (TnC), where it binds and promotes actin–myosin interactions. Relaxation of muscle requires the reuptake of Ca2+ into the SR, which is catalyzed by the SR/endoplasmic reticulum (ER) Ca2+ ATPase (SERCA) (Fig. 1C). PA is a small soluble protein that reversibly binds Ca2+ and is present in some muscles, with greater quantities in fast-twitch fibers. PA therefore might be expected to serve a facilitated diffusion role. However, the binding of Ca2+ by PA is too slow to promote equilibrium of [Ca2+], [PA] and [PACa2+] during a series of rapid contractions, and PA probably serves as a slow-acting temporal buffer which binds the excess Ca2+ that accumulates during consecutive contractions (Permyokov, 2006).
Cannell and Allen first evaluated Ca2+ cycling as a reaction–diffusion process in frog skeletal muscle, and these authors generated a mathematical simulation that compared well to experimental measurements of Ca2+ transients (Cannell and Allen, 1984). A principal finding was that substantial gradients in Ca2+ appear to exist over the sarcomere. Baylor and Hollingworth performed a similar analysis in frog skeletal muscle where they included the influence of Ca2+ binding to ATP (Baylor and Hollingworth, 1998). In addition to finding Ca2+ gradients that persisted for tens of milliseconds after release from the SR, they found that ATP serves to facilitate Ca2+ diffusion as ATP occurs in high concentrations and has a relatively high D. This allowed for a more uniform distribution across the sarcomere of Ca2+ that was bound to TnC, which may lead to a more unified contractile response. Baylor and Hollingworth also noted that the facilitated diffusion role played by ATP makes it a temporal buffer as well (Baylor and Hollingworth, 1998). That is, ATP binding and release of Ca2+ caused the free Ca2+ transient to be broader and of a lower magnitude than if ATP was absent or immobilized. This model was more recently applied to mammalian skeletal muscle, where it differed from the model for frog muscle in that the Ca2+ release sites were offset by 0.5 μm from the sarcomere _Z_-line, based on morphological studies (Baylor and Hollingworth, 2007). At a common temperature, positioning of the Ca2+ release sites near the middle of the thin filaments, as seen in mammals, had the advantage of promoting a more uniform distribution of Ca2+ in the TnC binding sites. This would seem to indicate that mammalian SR structure has been subjected to selective pressure to offset diffusion constraints that otherwise may limit contractile function.
Groenendaal and colleagues (Groenendaal et al., 2008) adapted the model of Baylor and Hollingworth (Baylor and Hollingworth, 1998) to explicitly examine the differences between mammalian and frog muscle at 35°C. Again, the models implied that steep concentration gradients existed for Ca2+ during contractions, and that [Ca2+] was 5-fold higher in the region of TnC than in other regions of the sarcomere in mouse and frog muscle. In addition, Groenendaal and colleagues showed that [Ca2+] was high in the region of the mitochondria, and they speculated that this arrangement facilitated Ca2+ activation of oxidative phosphorylation and helped balance ATP demand during contraction (Groenendaal et al., 2008), although it should be noted that their simulations analyzed fast-twitch fibers that rely primarily on anaerobic fuels (PCr, glucose) to power rapid contractions.
Nuclear function
Nuclei are associated with the transcription, translation and transport of a variety of molecules ranging in size from small metabolites to large complexes such as polysomes (Fig. 1D). Skeletal muscle fibers are multinucleated cells with the nuclei typically located at the periphery of the fiber, and each nucleus serves a volume of cytoplasm known as the myonuclear domain. The myonuclear domain has often been considered to be conserved in skeletal muscle, including during increases or decreases in fiber size (e.g. Allen et al., 1995; Roy et al., 1999; Bruusgaard et al., 2003; Bruusgaard et al., 2006; Brack et al., 2005), although this notion does not seem to be generally applicable and remains the source of debate (reviewed in Gundersen and Bruusgaard, 2008). Nevertheless, the size of the myonuclear domain presumably is regulated to ensure sufficient transcriptional capacity as well as limited distances over which nuclear substrates and products must travel to reach sites of action. There is evidence that transport within the myonuclear domain governs nuclear distribution at the sarcolemma, as mathematical analyses indicate that myonuclei in mammalian skeletal muscle have a uniform distribution at the sarcolemma (rather than a random distribution), which minimizes transport distances within the domain. This suggests that there are through-space signals that influence nuclear positioning (Bruusgaard et al., 2003; Bruusgaard et al., 2006).
The capacity for movement of nuclear products appears to be highly constrained in skeletal muscle, and proteins tend to remain in the vicinity of the nucleus from which they originated (Hall and Ralston, 1989; Pavlath et al., 1989; Ono et al., 1994). The distribution of mRNA and messenger ribonucleoprotein particles (mRNPs) in skeletal muscle is also consistent with greatly hindered diffusion, and it has been suggested that these large complexes are excluded from the myofibrillar space (Russell and Dix, 1992). However, Gauthier and Mason-Savas found ribosomes (and possibly polysomes) within the thick and thin filament lattice (Gauthier and Mason-Savas, 1993), suggesting that these large complexes have access to this region and may promote localized translation. It is also possible that diffusion constraints may be overcome in part by the extensive microtubule array in skeletal muscle, which is closely associated with the nuclei (Bruusgaard et al., 2006) and may be used in the trafficking of mRNA and proteins. A dynamic, anti-parallel microtubule network develops in growing myotubes, and it has been shown that myosin can be transported along these filaments by motor proteins (Pizon et al., 2005). Scholz and colleagues demonstrated that in fully differentiated cardiac myocytes microtubule-based transport is essential for the movement of mRNPs from the nucleus to sites of translation, and that disruption of the microtubule system inhibits protein synthesis (Scholz et al., 2008). To our knowledge, cytoskeleton-based transport of proteins or mRNA has not been demonstrated in mature skeletal muscle fibers. However, the microtubule network is closely associated with nuclei in mature skeletal muscle from mammals (e.g. Bruusgaard et al., 2006), crustaceans and fishes (Fig. 4), and it appears to be well suited for both positioning of nuclei (perhaps playing a role in controlling myonuclear domain size) and transporting nuclear products.
Fig. 4.
A 3-dimensional reconstruction of the microtubule array (orange) in and around nuclei (blue) from white skeletal muscle of the smooth butterfly ray (Gymnura micrura). The microtubule network may be involved in the positioning of nuclei and trafficking of nuclear products in fibers (see text).
Comparative analyses of muscle growth reveal mechanisms of avoiding diffusion limitation
While the vast majority of work on reaction–diffusion processes in muscle has focused on mammals, our labs have for the past several years examined muscles from non-traditional models that have properties that make them particularly informative. As described above, the extent to which diffusion influences metabolic processes is largely dependent on the interaction between reaction fluxes and diffusion distances (Fig. 2), and during animal growth this interaction can be altered. As an animal increases in body mass, muscles grow by a combination of increasing the number of fibers (hyperplasia) and increasing the size of individual fibers (hypertrophy). Thus, hypertrophic fiber growth leads to increasing diffusion distances for molecules like O2. Further, in animals such as fishes and crustaceans that undergo a very large post-metamorphic increase in body mass and have muscles that grow hypertrophically, fibers can greatly increase in diameter during animal growth. For instance, some juvenile crustaceans and fishes have muscle fibers that are <50 μm in diameter, but as the animals grow the fibers can increase in diameter to several hundred micrometers (Jahromi and Atwood, 1971; Hoyle, 1987; Weatherley and Gill, 1987; Boyle et al., 2003; Johnston et al., 2003; Johnston et al., 2004; Kinsey et al., 2007; Nyack et al., 2007; Jimenez et al., 2008; Jimenez et al., 2010; Hardy et al., 2009; Hardy et al., 2010). Thus, for processes where fiber size constitutes an important diffusion distance (as it does for aerobic metabolism and nuclear function), muscles from these animals demonstrate natural variation in one of the key properties that governs diffusion-dependent reaction fluxes.
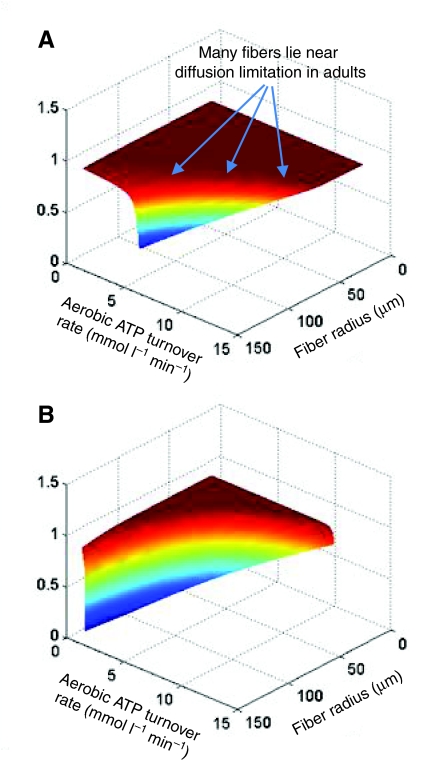
Previously measured values of diffusion in muscle (see above) were coupled with measurements of diffusion distances determined using confocal and transmission electron microscopy, and measurements of aerobic ATP turnover. Rates of aerobic ATP turnover were determined from measurements of mitochondrial volume density (Kinsey et al., 2007; Locke and Kinsey, 2008), from respiration rates of isolated mitochondria (Burpee et al., 2010), or from direct measurements of ATP turnover using NMR in isolated muscles or in vivo (Kinsey et al., 2005; Hardy et al., 2006; Nyack et al., 2007; Jimenez et al., 2008). These data as well as data from the literature were evaluated using a reaction–diffusion model and the application of the effectiveness factor (η), which has typically been used by engineers to assess the design of catalytic reactors (Weisz, 1973). η is the ratio of the observed reaction rate to the rate if diffusion were not limiting, and this ratio can be calculated if the diffusion coefficients, diffusion distances and reaction rates are known. Therefore, if η=1, diffusion is not limiting, whereas if it is 0.5, the observed rate is 50% of what it would be if diffusion was not constraining the reaction. Our models are admittedly simple representations of fibers, treating them as bioreactors and not accounting for all kinetic regulatory mechanisms, enzyme localization or potential channeling of substrates. However, they allow us to ask the general question in a wide range of muscle types: for a given set of D values, diffusion distances and rates of ATP turnover, does diffusion limit aerobic flux? Using this approach, we have found that aerobic flux in muscle fibers typically is not diffusion limited, but fibers are often on the brink of substantial limitation (Kinsey et al., 2007; Locke and Kinsey, 2008; Jimenez et al., 2008; Hardy et al., 2009; Dasika et al., 2011). That is, many muscles have a combination of ATP turnover rates and diffusion distances that maintain a high η, but if aerobic flux or diffusion distances were to increase further, a substantial drop in η would occur. Further, in cases where we have examined muscles that grow hypertrophically, we found that fibers only approach diffusion limitation in adults, suggesting that diffusion may play a role in muscle structure and growth patterns (see below; Fig. 5). It is interesting to note that Weisz originally suggested that biological reaction–diffusion processes would function near the edge of diffusion limitation (Weisz, 1973) and we have found that this often occurs in skeletal muscle.
Fig. 5.
Example of the interaction between the effectiveness factor (η), aerobic ATP turnover rate and fiber radius for (A) a high blood [O2] (35 μmol l–1) and (B) a low blood [O2] (8 μmol l–1). When η<1, diffusion of O2 or intracellular metabolites like ATP limits aerobic reaction flux. This surface was modeled for fibers that have 10% of the cell volume devoted to mitochondria. In principle, fibers with a similar mitochondrial volume density can be designated as points on the surface, and changes in fibers (e.g. hypertrophic growth) can be represented by contours on the surface. All fibers examined so far have aerobic fluxes and diffusion distances that place them on the upper part of the surface under aerobic conditions (η≈1), but many are near the edge of diffusion limitation, particularly as adults (not shown). Note that a reduced blood [O2] makes fibers more susceptible to diffusion limitation.
Skeletal muscle also is subject to metabolic and structural alterations to avoid diffusion limitation. A particularly informative model has been the swimming muscle of the blue crab, Callinectes sapidus, which has fibers that increase in size during hypertrophic growth from <50 μm in juveniles to >600 μm in adults (Boyle et al., 2003). These muscles are composed of light fibers, which are used for burst contractions and have sparse mitochondria, dark fibers, which are rich in mitochondria and power sustained swimming, and a small number of intermediate fibers. As diffusion distances increase with animal growth, the light and dark fibers respond in different ways to avoid diffusion limitation. As the light fibers grow hypertrophically, they rely increasingly on anaerobic metabolism to speed up key phases of post-contractile recovery. That is, the small fibers from juveniles produce no lactate and consume little glycogen after burst contraction, but the large fibers of adults produce copious amounts of lactate and consume glycogen post-contraction (Boyle et al., 2003; Johnson et al., 2004). This allows phosphagen resynthesis to occur faster than our reaction–diffusion model predicted that it should in the large fibers (Kinsey et al., 2005). Of course, this puts the animal deeper into oxygen debt, but it has the immediate advantage of allowing a more rapid recovery of high-force contractile function.
The light fibers also undergo structural modifications to compensate for hypertrophic growth. As fibers get larger, the mitochondria shift from a uniform distribution with both peripheral (subsarcolemmal) and central (intermyofibrillar) mitochondria in juveniles, to an almost exclusively subsarcolemmal distribution in adults, where nearly 90% of the mitochondria are clustered at the sarcolemma (Boyle et al., 2003; Hardy et al., 2009). Thus, the mitochondria are moving closer to the source of the substrate, O2, but this creates diffusion distances of hundreds of micrometers for the product, ATP, in these very large fibers (Fig. 1A,B). This suggests that O2 diffusion is a greater constraint than is ATP diffusion. Reaction–diffusion models demonstrated that this shift in distribution allows the muscle to maintain a high η and achieve the experimentally measured rate of aerobic ATP turnover, whereas if the mitochondria had maintained a uniform mitochondrial distribution throughout fiber growth, the fibers would be highly diffusion limited (very low η) in adults and they would attain only a fraction of the observed rate of aerobic flux (Hardy et al., 2009).
In contrast to mitochondria, nuclei undergo a shift in distribution during hypertrophic growth that is the opposite of that seen for mitochondria. In small fibers of juveniles, nuclei have a subsarcolemmal distribution, as is typical of mammalian fibers. However, as the fibers grow to large sizes, not only are more nuclei recruited to the fiber but also they become uniformly distributed throughout the fiber (subsarcolemmal and intermyofibrillar). This also appears to be a response to diffusion constraints. Nuclei do not require O2 like mitochondria, but they rely on the transport of macromolecules that diffuse very slowly in muscle (see above). By both increasing the nuclear number and altering the distribution, the fibers preserve both the size of the myonuclear domain and the maximal diffusion distances within that domain. Reaction–diffusion analyses again reveal that rates of nuclear processes are three orders of magnitude greater than they would be if this distributional change had not occurred (Hardy et al., 2009). The structural changes seen in blue crab light fibers are shown schematically in Fig. 6A.
Fig. 6.
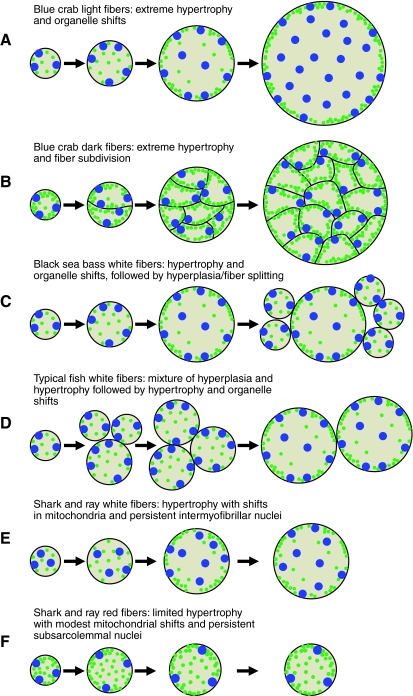
Patterns of post-metamorphic fiber growth and organelle distribution that lead to an avoidance of diffusion limitation during animal growth. Green: mitochondria; blue: nuclei. (A) Blue crab light muscle. As the fibers grow hypertrophically through most of post-metamorphic development to very large sizes, mitochondria shift from a uniform distribution (subsarcolemmal and intermyofibrillar) toward the fiber periphery (subsarcolemmal) and nuclei do the opposite. These fibers also rely increasingly on anaerobic metabolism to increase post-contractile recovery during fiber growth. (B) Blue crab dark muscle. The fibers become increasingly subdivided during hypertrophic growth, and develop intracellular perfusion. The subdivisions are isolated from one another and represent the metabolic functional unit, while the fiber as a whole represents the contractile functional unit. (C) Black sea bass white muscle. The muscles grow hypertrophically through most of post-metamorphic development and undergo a shift in mitochondrial and nuclear distribution as in blue crab light muscle. However, as the fibers approach diffusion limitation of aerobic metabolism, there is an onset of hyperplasic growth that leads to shorter diffusion distances. (D) Typical pattern of fish white muscle growth. Hyperplasia is a dominant form of muscle growth early in life (often accompanied by hypertrophy), followed by nearly exclusive hypertrophic growth. The duration of the hyperplasic growth period will impact the fiber size in adults. This pattern is similar in fish red muscle and in mammalian muscle, but the fibers do not grow as large as in white muscle. (E) White muscle from sharks and rays. Mitochondria shift distribution during hypertrophic growth as in other muscle, but the nuclei have a largely intermyofibrillar distribution, even when the fibers are small. Here, the nuclei are not responding to changing diffusion constraints, but are prepared for impending constraints in the adult. (F) Red muscle from sharks and rays. The red muscles undergo a modest shift in mitochondria, but the nuclei are subsarcolemmal throughout fiber growth. Unlike the white fibers in E, the red fibers will not grow large (due to diffusion constraints associated with aerobic metabolism) and a subsarcolemmal nuclear placement is therefore not problematic. See text for additional details.
The blue crab also has aerobic (dark) fibers that power sustained swimming, which require much higher rates of aerobic ATP turnover and respond very differently from the burst (light) fibers. These fibers become increasingly subdivided as the fibers grow larger, creating both short intracellular diffusion distances during growth and intrafiber perfusion. Within a subdivision, mitochondrial and nuclear distributions are very reminiscent of a mammalian fiber, and FRAP experiments demonstrated that neighboring subdivisions do not exchange small molecules. Thus, the subdivisions represent independent metabolic functional units of the fiber. However, innervation patterns revealed that the fiber as a whole remains the contractile functional unit. Thus, the aerobic fibers have solved design constraints by reducing diffusion distances for aerobic metabolism, which is constrained by diffusion, but preserving the structures associated with contraction, which is not limited by diffusion (Fig. 6B). Mathematical reaction–diffusion models again showed that all of the changes described above in the aerobic fibers are essential for the muscle to support the observed rates of ATP turnover (Hardy et al., 2009).
We have since shown that these design features in light and dark muscle from a variety of swimming and non-swimming crabs are generally applicable and independent of phylogeny. This indicates that they are adaptive responses to diffusion constraints that depend on fiber (and body) size and functional demand (Hardy et al., 2010). We have seen the same shifts in mitochondrial (Nyack et al., 2007) and nuclear distribution (C. Priester, L. C. Morton, S.T.K., W. O. Watanabe and R.M.D., submitted) during hypertrophic growth in white muscle from black sea bass (Centropristis striata), suggesting that these subcellular responses may be widespread. Further, as black sea bass continue to grow, the pattern of fiber growth shifts from hypertrophy to hyperplasia (or fiber splitting), leading to shorter average diffusion distances. That is, as the organelle distributions change and our mathematical analysis of η indicates that the fibers are approaching diffusion limitation, the muscle growth pattern is altered to preserve η (Fig. 6C). This is at odds with the paradigm for fish white muscle growth, which generally entails a mix of hypertrophy and hyperplasia early in post-metamorphic development (called mosaic hyperplasia) followed by hypertrophic growth (Fig. 6D). In red and white muscle from cartilaginous fishes (Atlantic sharpnose shark, Rhizoprionodon terraenovae, and smooth butterfly ray,G. micrura), a similar, but more modest shift in mitochondrial distribution occurs with hypertrophic growth. However, nuclear distribution appears to be part of the developmental program, rather than a direct response to diffusion constraints that arise during growth. In red fibers, nuclei have a subsarcolemmal distribution throughout growth, but in white fibers, the nuclei have a uniform (subsarcolemmal and intermyofibrillar) distribution at all stages of growth. That is, white fibers have intermyofibrillar nuclei in juveniles, even when they are the same size as the red fibers. Thus, the small white fibers in juveniles have a nuclear distribution that will be functional when the fibers grow to large dimensions in adults, whereas the subsarcolemmal distribution in the red fibers will also be functional at all stages as they will not grow large (Fig. 6E,F) (C. Priester, personal communication). Thus, the fibers in cartilaginous fishes are using a different mechanism to achieve the same end result as in other groups described above, and they therefore avoid diffusion constraints in the large fibers of adults.
Conclusions
Skeletal muscle fibers are highly ordered and contain many intracellular barriers that impede diffusion, and measurements of diffusion in muscle for a wide range of molecules indicate that the intracellular environment behaves as a porous medium. This does not discount the importance of enzyme localization, specific binding or transport along the cytoskeleton, all of which may be mechanisms to avoid diffusion limitation of certain processes. Examination of a variety of species and muscle types with fibers that undergo hypertrophic growth, and application of simple reaction–diffusion mathematical models indicate that most fibers are not limited by diffusion per se. However, many fibers seem to be near diffusion limitation, particularly in adults, and changes in metabolic organization and growth patterns appear to be aimed at avoiding diffusion constraints. This implies that intracellular signals that govern processes like mitochondrial biogenesis/degradation or nuclear position are spatially variable across the cell, and changes in fiber growth can be altered by signals associated with diffusion limitation.
Footnotes
This research was supported by grants from the National Science Foundation (IOS-0719123 to S.T.K. and R.M.D. and IOS-0718499 to B.R.L.) and from the National Institute of Arthritis and Musculoskeletal and Skin Diseases (R15-AR-052708 to S.T.K.). Deposited in PMC for release after 12 months.
References
- Agutter P. S., Malone P. C., Wheatley D. N. (1995). Intracellular transport mechanisms: a critique of diffusion theory. J. Theor. Biol. 176, 261-272 [DOI] [PubMed] [Google Scholar]
- Aliev M. K., Tikhonov A. N. (2004). Random walk analysis of restricted metabolite diffusion in skeletal myofibril systems. Mol. Cell. Biochem. 256/257, 257-266 [DOI] [PubMed] [Google Scholar]
- Allen D. L., Monke S. R., Talmadge R. J., Roy R. R., Edgerton V. R. (1995). Plasticity of myonuclear number in hypertrophied and atrophied mammalian skeletal muscle fibers. J. Appl. Physiol. 78, 1969-1976 [DOI] [PubMed] [Google Scholar]
- Arrio-Dupont M., Cribier S., Foucault G., Devaux P. F., d’Albis A. (1996). Diffusion of fluorescently labeled macromolecules in cultured muscle cells. Biophys. J. 70, 2327-2332 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arrio-Dupont M., Foucault G., Vacher M., Douhou A., Cribier S. (1997). Mobility of creatine phosphokinase and β enolase in cultured muscle cells. Biophys. J. 73, 2667-2673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arrio-Dupont M., Foucault G., Vacher M., Devaux P. F., Cribier S. (2000). Translational diffusion of globular proteins in the cytoplasm of cultured muscle cells. Biophys. J. 78, 901-907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor S. M., Hollingworth S. (1998). Model of sarcomeric Ca2+ movements, including ATP Ca2þ binding and diffusion, during activation of frog skeletal muscle. J. Gen. Physiol. 112, 297-316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor S. M., Hollingworth S. (2007). Simulation of Ca2+ movements within the sarcomere of fast-twitch mouse fibers stimulated by action potential. J. Gen. Physiol. 130, 283-302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylor S. M., Pape P. C. (1988). Measurement of myoglobin diffusivity in the myoplasm of frog skeletal muscle fibers. J. Physiol. 406, 247-275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beard D. A. (2005). A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation. PLoS Comput. Biol. 1, e36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beard D. A., Kushmerick M. J. (2009). Strong inference for systems biology. PLoS Comput. Biol. 5, e1000459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernengo J. C., Collet C., Jacquemond V. (2001). Intracellualr Mg2+ diffusion within isolated rat skeletal muscle fibers. Biophys. Chem. 89, 35-51 [DOI] [PubMed] [Google Scholar]
- Bessman S. P., Geiger P. J. (1981). Transport of energy in muscle: the phophorylcreatine shuttle. Science 211, 448-452 [DOI] [PubMed] [Google Scholar]
- Boyle K. L., Dillaman R. M., Kinsey S. T. (2003). Mitochondrial distribution and glycogen dynamics suggest diffusion constraints in muscle fibers of the blue crab, Callinectes sapidus. J. Exp. Zool. 297A, 1-16 [DOI] [PubMed] [Google Scholar]
- Brack A. S., Bildsoe H., Hughes S. M. (2005). Evidence that satellite cell decrement contributes to preferential decline in nuclear number from large fibres during murine age-related muscle atrophy. J. Cell Sci. 118, 4813-4821 [DOI] [PubMed] [Google Scholar]
- Bruusgaard J. C., Liestøl K., Ekmark M., Kollstad K., Gunderson K. (2003). Number and spatial distribution of nuclei in the muscle fibers of normal mice studied in vivo. J. Physiol. 551, 467-478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruusgaard J. C., Liestøl K., Gunderson K. (2006). Distribution of myonuclei and microtubules in live muscle fibers of young, middle-aged, and old mice. J. Appl. Physiol. 100, 2024-2030 [DOI] [PubMed] [Google Scholar]
- Bunch W. H., Kallsen G. (1969). Rate of intracellular diffusion as measured in barnacle muscle. Science 164, 1178-1179 [DOI] [PubMed] [Google Scholar]
- Burpee J. L., Bardsley E. L., Dillaman R. M., Watanabe W. O., Kinsey S. T. (2010). Scaling with body mass of mitochondrial respiration from the white muscle of three phylogenetically, morphologically, and behaviorally disparate teleost fishes. J. Comp. Physiol. B Biochem. Syst. Environ. Physiol. 180, 967-977 [DOI] [PubMed] [Google Scholar]
- Cannell M. B., Allen D. G. (1984). Model of calcium movements during activation in the sarcomere of frog skeletal muscle. Biophys. J. 45, 913-925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleveland G. G., Chang D. C., Hazlewood C. F., Rorschach H. E. (1976). Nuclear magnetic resonance measurement of skeletal muscle: anisotropy of the diffusion coefficient of intracellular water. Biophys. J. 16, 1043-1053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conley K. E., Ordway G. A., Richardson R. S. (2000). Deciphering the mysteries of myoglobin in striated muscle. Acta Physiol. Scand. 168, 623-634 [DOI] [PubMed] [Google Scholar]
- Dash R. K., Li Y., Kim J., Beard D. A., Saidel G. M., Cabrera M. E. (2008). Metabolic dynamics in skeletal muscle during acute reduction in blood flow and oxygen supply to mitochondria: in-silico studies using a multi-scale, top-down integrated model. PLoS ONE 3, e3168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dasika S. K., Kinsey S. T., Locke B. R. (2011). Reaction-diffusion constraints in living tissue: effectiveness factors in skeletal muscle design. Biotech. Bioeng. 108, 104-115 [DOI] [PubMed] [Google Scholar]
- de Graaf R. A., van Kranenburg A., Nicolay K. (2000). In vivo 31P-NMR diffusion spectroscopy of ATP and phosphocreatine in rat skeletal muscle. Biophys. J. 78, 1657-1664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Graaf R. A., Braun K. P. J., Nicolay K. (2001). Single-shot diffusion trace 1H NMR spectroscopy. Magn. Reson. Med. 45, 741-748 [DOI] [PubMed] [Google Scholar]
- Dix D. J., Eisenberg B. R. (1988). In situ hybridization and immunocytochemistry in serial sections of rabbit skeletal muscle to detect myosin expression. J. Histochem. Cytochem. 6, 1519-1526 [DOI] [PubMed] [Google Scholar]
- Dzeja P. P., Terzic A. (2003). Phosphotransfer networks and cellular energetic. J. Exp. Biol. 206, 2039-2047 [DOI] [PubMed] [Google Scholar]
- Egginton S., Sidell B. D. (1989). Thermal acclimation induces adaptive changes in subcellular structure of fish skeletal muscle. Am. J. Physiol. 256, R1-R9 [DOI] [PubMed] [Google Scholar]
- Egginton S., Skilbeck C., Hoofd L., Calvo J., Johnston I. A. (2002). Peripheral oxygen transport in skeletal muscle of Antarctic and sub-Antarctic notothenioid fish. J. Exp. Biol. 205, 769-779 [DOI] [PubMed] [Google Scholar]
- Ellington W. R. (2001). Evolution and physiological roles of phosphagen systems. Annu. Rev. Physiol. 63, 289-325 [DOI] [PubMed] [Google Scholar]
- Federspiel W. J. (1986). A model study of intracellular oxygen gradients in a myoglobin containing skeletal muscle fiber. Biophys. J. 49, 857-868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flögel U., Merx M. W., Gödecke A., Decking U. K. M., Schrader J. (2001). Myoglobin: a scavenger of bioactive NO. Proc. Natl. Acad. Sci. USA 98, 735-740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fushimi K., Verkman A. S. (1991). Low viscosity in the aqueous domain of cell cytoplasm measured by picoseconds polarization microfluorimetry. J. Cell Biol. 112, 719-725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galban C. J., Maderwald S., Uffmann K., de Greiff A., Ladd M. E. (2004). Diffusive sensitivity to muscle architecture: a magnetic resonance diffusion tensor imaging study of the human calf. Eur. J. Appl. Physiol. 93, 253-262 [DOI] [PubMed] [Google Scholar]
- Gauthier G. F., Mason-Savas A. (1993). Ribosomes in the skeletal muscle filament lattice. Anat. Rec. 237, 149-156 [DOI] [PubMed] [Google Scholar]
- Gödecke A., Flögel U., Zanger K., Ding Z., Hirchenhain J., Decking U. K. M., Schrader J. (1999). Disruption of myoglobin in mice induces multiple compensatory mechanisms. Proc. Natl. Acad. Sci. USA 96, 10495-10500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groebe K. (1995). An easy to use model for O2 supply to red muscle. Validity of assumptions, sensitivity to errors in data. Biophys. J. 68, 1246-1269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groenendaal W., Jeneson J. A. L., Verhoog P. J., van Riel N. A. W., Ten Eikelder H. M. M., Nicolay K., Hilbers P. A. J. (2008). Computational modelling identifies the impact of subtle anatomical variations between amphibian and mammalian skeletal muscle on spatiotemporal calcium dynamics. IET Syst. Biol. 2, 411-422 [DOI] [PubMed] [Google Scholar]
- Gundersen K., Bruusgaard J. C. (2008). Nuclear domains during muscle atrophy: nuclei lost or paradigm lost? J. Physiol. 586, 2675-2681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall Z. W., Ralston E. (1989). Nuclear domains in muscle cells. Cell 59, 771-772 [DOI] [PubMed] [Google Scholar]
- Hardy K. M., Dillaman R. M., Locke B. R., Kinsey S. T. (2009). A skeletal muscle model of extreme hypertrophic growth reveals the influence of diffusion on cellular design. Am. J. Physio., Int. Comp. Reg. Physiol. 296, R1855-R1867 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy K. M., Locke B. R., Da Silva M., Kinsey S. T. (2006). A reaction-diffusion analysis of energetics in large muscle fibers secondarily evolved for aerobic locomotor function. J. Exp. Biol. 209, 3610-3620 [DOI] [PubMed] [Google Scholar]
- Hardy K. M., Lema S. C., Kinsey S. T. (2010). The metabolic demands of swimming behavior influence the evolution of skeletal muscle fiber design in the brachyuran crab family Portunidae. Mar. Biol. 157, 221-236 [Google Scholar]
- Hill A. V. (1965). Trials and Trails in Physiology, pp. 217-218 London: E. Arnold, Limited; [Google Scholar]
- Hochachka P. (1999). The metabolic implications of intracellular circulation. Proc. Natl. Acad. Sci. USA 96, 12233-12239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan M. C., Stary C. M., Balaban R. S., Combs C. A., (2005). NAD(P)H fluorescence imaging of mitochondrial metabolism in contracting Xenopus skeletal muscle fibers: effect of oxygen availability. J. Appl. Physiol. 98, 1420-1426 [DOI] [PubMed] [Google Scholar]
- Hoofd L., Egginton S. (1997). The possible role of intracellular lipid in oxygen delivery to fish skeletal muscle. Respir. Physiol. 107, 191-202 [DOI] [PubMed] [Google Scholar]
- Hoppeler H., Weibel E. R. (1998). Limits for oxygen and substrate transport in mammals. J. Exp. Biol. 201, 1051-1064 [DOI] [PubMed] [Google Scholar]
- Hoyle G. (1987). The giant muscle cells of barnacles. In Crustacean Issues 5, Barnacle Biology (ed. Southward A. J.), pp. 213-225 Netherlands: A. A. Balkema; [Google Scholar]
- Hubley M. J., Moerland T. S. (1995). Application of homonuclear decoupling to measures of diffusion in biological 31P-spin echo spectra. NMR Biomed. 8, 113-117 [DOI] [PubMed] [Google Scholar]
- Hubley M. J., Rosanske R. C., Moerland T. S. (1995). Diffusion coefficients of ATP and creatine phosphate in isolated muscle: pulsed gradient 31P-NMR of small biological samples. NMR Biomed. 8, 72-78 [DOI] [PubMed] [Google Scholar]
- Hubley M. J., Locke B. R., Moerland T. S. (1997). Reaction-diffusion analysis of effects of temperature on high-energy phosphate dynamics in goldfish skeletal muscle. J. Exp. Biol. 200, 975-988 [DOI] [PubMed] [Google Scholar]
- Jahromi S. S., Atwood H. L. (1971). Electrical coupling and growth in lobster muscle fibers. Can. J. Zool. 49, 1029-1034 [DOI] [PubMed] [Google Scholar]
- Jimenez A. G., Locke B. R., Kinsey S. T. (2008). The influence of oxygen and high-energy phosphate diffusion on metabolic scaling in three species of tail-flipping crustaceans. J. Exp. Biol. 211, 3214-3225 [DOI] [PubMed] [Google Scholar]
- Jimenez A. G., Kinsey S. T., Dillaman R. M., Kapraun D. F. (2010). Nuclear DNA content variation associated with muscle fiber hypertrophic growth in decapod crustaceans. Genome 53, 161-171 [DOI] [PubMed] [Google Scholar]
- Johnson L. K., Dillaman R. M., Gay D. M., Blum J. E., Kinsey S. T. (2004). Metabolic influences of fiber size in aerobic and anaerobic muscles of the blue crab, Callinectes sapidus. J. Exp. Biol. 207, 4045-4056 [DOI] [PubMed] [Google Scholar]
- Johnston I. A. (1982). Capillarisation, oxygen diffusion distances and mitochondrial content of carp muscles following acclimation to summer and winter temperatures. Cell Tissue Res. 222, 525-537 [DOI] [PubMed] [Google Scholar]
- Johnston I. A., Fernández D. A., Calvo J., Vieira V. L. A., North A. W., Abercromby M., Garland T., Jr (2003). Reduction in muscle fibre number during the adaptive radiation of notothenioid fishes: a phylogenetic perspective. J. Exp. Biol. 206, 2595-2609 [DOI] [PubMed] [Google Scholar]
- Johnston I. A., Abercromby M., Vieira V. L. A., Sigursteindóttir R. J., Kristjánsson B. K., Sibthorpe D., Skúlason S. (2004). Rapid evolution of muscle fibre number in post-glacial populations of charr Salvelinus alpinus. J. Exp. Biol. 207, 4343-4360 [DOI] [PubMed] [Google Scholar]
- Jurgens K. D., Peters T., Gros G. (1994). Diffusitivity of myoglobin in intact skeletal muscle cells. Proc. Natl. Acad. Sci. USA 91, 3829-3833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurgens K. D., Papadopoulos S., Peters T., Gros G. (2000). Myoglobin: just an oxygen store or also an oxygen transporter? News Physiol. Sci. 15, 269-274 [DOI] [PubMed] [Google Scholar]
- Kinsey S. T., Ellington W. R. (1996). 1H- and 31P-Nuclear magnetic resonance studies of L-lactate transport in isolated muscle fibers from the spiny lobster, Panulirus argus. J. Exp. Biol. 199, 2225-2234 [DOI] [PubMed] [Google Scholar]
- Kinsey S. T., Moerland T. S. (2002). Metabolite diffusion in giant muscle fibers of the spiny lobster, Panulirus argus. J. Exp. Biol. 205, 3377-3386 [DOI] [PubMed] [Google Scholar]
- Kinsey S. T., Penke B., Locke B. R., Moerland T. S. (1999). Diffusional anisotropy is induced by subcellular barriers in skeletal muscle. NMR Biomed. 11, 1-7 [DOI] [PubMed] [Google Scholar]
- Kinsey S. T., Pathi P., Hardy K. M., Jordan A., Locke B. R. (2005). Does metabolite diffusion limit post-contractile recovery in burst locomotor muscle? J. Exp. Biol. 208, 2641-2652 [DOI] [PubMed] [Google Scholar]
- Kinsey S. T., Hardy K. M., Locke B. R. (2007). The long and winding road: influences of intracellular metabolite diffusion on cellular organization and metabolism in skeletal muscle. J. Exp. Biol. 210, 3505-3512 [DOI] [PubMed] [Google Scholar]
- Kongas O., Wagner M. J., ter Veld F., Nicolay K., van Beek J. H. G. M., Krab K. (2004). The mitochondrial outer membrane is not a major diffusion barrier for ADP in mouse heart skinned fibre bundles. Pflugers Arch. 447, 840-844 [DOI] [PubMed] [Google Scholar]
- Korzeniewski B. (2003). Regulation of oxidative phosphorylation in different muscles and various experimental conditions. Biochem. J. 375, 799-804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krogh A. (1919). The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. J. Physiol. 52, 409-415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kushmerick M. J., Podolsky R. J. (1969). Ionic mobility in muscle cells. Science 166, 1297-1298 [DOI] [PubMed] [Google Scholar]
- Lai N., Saidel G. M., Grassi B., Gladden L. B., Cabrera M. E. (2007). Model of oxygen transport and metabolism predicts effect of hyperoxia on canine muscle oxygen uptake dynamics. J. Appl. Physiol. 103, 1366-1378 [DOI] [PubMed] [Google Scholar]
- Lambeth M. J., Kushmerick M. J. (2002). A computational model for glycogenolysis in skeletal muscle. Annu. Biomed. Eng. 30, 808-827 [DOI] [PubMed] [Google Scholar]
- Lin P. C., Kreutzer U., Jue T. (2007). Anisotropy and temperature dependence of myoglobin translational diffusion in myocardium: implication for oxygen transport and cellular architecture. Biophys. J. 92, 2608-2620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingston D. J., La Mar G. N., Brown W. D. (1983). Myoglobin diffusion in bovine heart muscle. Science 220, 71-73 [DOI] [PubMed] [Google Scholar]
- Locke B. R. (2001). Electro-transport in hydrophilic nanostructured materials. In Nano-Surface Chemistry (ed. Rosoff M.), pp. 527-624 New York: Marcel Dekker, Incorporated; [Google Scholar]
- Locke B. R., Kinsey S. T. (2008). Diffusional constraints on energy metabolism in skeletal muscle. J. Theor. Biol. 254, 417-429 [DOI] [PubMed] [Google Scholar]
- Luby-Phelps K. (2000). Cytoarchitechture and physical properties of the cytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 192, 189-221 [DOI] [PubMed] [Google Scholar]
- Luby-Phelps K., Mujumdar S., Mujumdar R. B., Ernst L. A., Galbraith W., Waggoner A. S. (1993). A novel fluorescence ratiometric method confirms the low solvent viscosity of the cytoplasm. Biophys. J. 65, 236-242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainwood G. W., Raukusan K. (1982). A model for intracellular energy transport. Can. J. Physiol. Pharmacol. 60, 98-102 [DOI] [PubMed] [Google Scholar]
- Maughan D. W., Godt R. E. (1999). Parvalbumin concentration and diffusion coefficient in frog myoplasm, J. Muscle Res. Cell Motil. 20, 199-209 [DOI] [PubMed] [Google Scholar]
- Maughan D., Lord C. (1988). Protein diffusivities in skinned frog skeletal muscle fibers. In Molecular Mechanism of Muscle Contraction (ed. Sugi H., Pollack G. H.), pp. 75-84, New York: Plenum; [PubMed] [Google Scholar]
- Meyer R. A., Sweeney H. L., Kushmerick M. J. (1984). A simple analysis of the ‘phosphocreatine shuttle. Am. J. Physiol. 246, C365-C377 [DOI] [PubMed] [Google Scholar]
- Moonen C. T. W., van Zijl P. C. M., Le Bihan D., DesPres D. (1990). In vivo NMR diffusion spectroscopy: 31P application to phosphorus metabolites in muscle. Magn. Reson. Med. 13, 467-477 [DOI] [PubMed] [Google Scholar]
- Nicolay K., Braun K. P. J., de Graaf R. A., Dijkhuizen R. M., Kruiskamp M. J. (2001). Diffusion NMR spectroscopy. NMR Biomed. 14, 94-111 [DOI] [PubMed] [Google Scholar]
- Nyack A. C., Locke B. R., Valencia A., Dillaman R. M., Kinsey S. T. (2007). Scaling of post-contractile PCr recovery in fish white muscle: effect of intracellular diffusion. Am. J. Physiol. 292, R2077-R2088 [DOI] [PubMed] [Google Scholar]
- O’Brien K. M., Mueller I. A. (2010). The unique mitochondrial form and function of Antarctic Channichthyid icefishes. Integr. Comp. Biol. 50, 993-1008 [DOI] [PubMed] [Google Scholar]
- Ono T., Ono K., Mizukawa K., Ohta T., Tsuchiya T., Tsuda M. (1994). Limited diffusibility of gene products directed by a single nucleus in the cytoplasm of multinucleated myofibers. FEBS Lett. 337, 18-22 [DOI] [PubMed] [Google Scholar]
- Ordway G. A., Garry D. J. (2004). Myoglobin: an essential haemoprotein in striated muscle. J. Exp. Biol. 207, 3441-3446 [DOI] [PubMed] [Google Scholar]
- Papadopoulos S., Jurgens K. D., Gros G. (1995). Diffusion of myoglobin in skeletal muscle cells: dependence on fibre tybe, contraction and temperature. Eur. J. Physiol. 430, 519-525 [DOI] [PubMed] [Google Scholar]
- Papadopoulos S., Jürgens K. D., Gros G. (2000). Protein diffusion in living skeletal muscle fibers: dependence on protein size, fiber type, and contraction. Biophys. J. 79, 2084-2094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papadopoulos S., Endeward V., Revesz-Walker B., Jurgens K. D., Gros G. (2001). Radial and longitudinal diffusion of myoglobin in single living heart and skeletal muscle cells. Proc. Natl. Acad. Sci. USA 98, 5904-5909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlath G. K., Rich K., Webster S. G., Blau H. M. (1989). Localization of muscle gene products in nuclear domains. Nature 337, 570-573 [DOI] [PubMed] [Google Scholar]
- Permyokov E. A. (2006). Parvalbumin, pp. 84-114 Hauppage, NY: Nova Biomedical; [Google Scholar]
- Piiper J. (2000). Perfusion, diffusion and their heterogeneities limiting blood-tissue O2 transfer in muscle. Acta Physiol. Scand. 168, 603-607 [DOI] [PubMed] [Google Scholar]
- Pizon V., Gerbal F., Cifuentes Diaz C., Karsenti E. (2005). Microtubule-dependent transport and organization of sarcomeric myosin during skeletal muscle differentiation. EMBO J. 24, 3781-3792 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy R. R., Monke S. R., Allen D. L., Edgerton V. R. (1999). Modulation of myonuclear number in functionally overloaded and exercised rat plantaris fibers. J. Appl. Physiol. 87, 634-642 [DOI] [PubMed] [Google Scholar]
- Russell B., Dix D. J. (1992). Mechanisms for intracellular distribution of mRNA: in situ hybridization studies in muscle. Am. J. Physiol. 262, C1-C8 [DOI] [PubMed] [Google Scholar]
- Saks V., Beraud N., Walliman T. (2008). Metabolic compartmentation – a system level property of muscle cells. Int. J. Mol. Sci. 9, 751-767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholander P. F. (1960). Oxygen transport through hemoglobin solutions. Science 131, 585-590 [DOI] [PubMed] [Google Scholar]
- Scholz D., Baicu C. F., Tuxworth W. J., Xu L., Kasiganesan H., Menick D. R., Cooper G., IV (2008). Microtubule dependent distribution of mRNA in adult cardiomyocytes. Am. J. Physiol. Heart Circ. Physiol. 294, H1135-H1144 [DOI] [PubMed] [Google Scholar]
- Shorten P. R., Sneyd J. (2009). A mathematical analysis of obstructed diffusion within skeletal muscle. Biophys. J. 96, 4764-4778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidell B. D. (1998). Intracellular oxygen diffusion: the roles of myoglobin and lipid at cold body temperature. J. Exp. Biol. 201, 1118-1127 [DOI] [PubMed] [Google Scholar]
- Sidell B. D., O’Brien K. M. (2006). When bad things happen to good fish: the loss of hemoglobin and myoglobin expression in Antarctic icefishes. J. Exp. Biol. 209, 1791-1802 [DOI] [PubMed] [Google Scholar]
- Suarez R. K. (1998). Design of glycolytic and oxidative capacities in muscles. In Principles of Animal Design – The Optimization and Symmorphosis Debate (ed. Weibel E. R., Taylor C. R., Bolis L.), pp. 155-163 Cambridge: Cambridge University Press; [Google Scholar]
- Suarez R. K. (2003). Shaken and stirred: muscle structure and metabolism. J. Exp. Biol. 206, 2021-2029 [DOI] [PubMed] [Google Scholar]
- van der Laarse W. J., des Tombe A. L., van Beek-Harmsen B. J., Lee-de Groot M. B. E., Jaspers R. T. (2005). Krogh’s diffusion coefficient for oxygen in isolate Xenopus skeletal muscle fibers and myocardial trabeculae at maximum rates of oxygen consumption. J. Appl. Physiol. 99, 2173-2180 [DOI] [PubMed] [Google Scholar]
- van Gelderen P., DesPres D., van Zijl P. C. M., Moonen C. T. W. (1994). Evaluation of restricted diffusion in cylinders. Phosphocreatine in rabbit leg muscle. J. Magn. Reson. 103B, 255-260 [DOI] [PubMed] [Google Scholar]
- van Wessel T., de Haan A., van der Laarse W. J. (2010). The muscle fiber type–fiber size paradox: hypertrophy or oxidiative metabolism. Eur. J. Appl. Physiol. 110, 665-694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verkman A. S. (2003). Diffusion in cells measured by fluorescence recovery after photobleaching. Methods Enzymol. 360, 635-648 [DOI] [PubMed] [Google Scholar]
- Vicini P., Kushmerick M. (2000). Cellular energetics analysis by a mathematical model of energy balance: estimation of parameters in human skeletal muscle. Am. J. Physiol. 279, C213-C224 [DOI] [PubMed] [Google Scholar]
- Wagner P. D. (2000). Diffusive resistance to O2 transport in muscle. Acta Physiol. Scand. 168, 609-614 [DOI] [PubMed] [Google Scholar]
- Walliman T. M., Wyss M., Brdiczka D., Nicolay K., Eppenberger H. M. (1992). Intracellular compartmentation, structure and function of creatine kinase isoenzymes in tissues with high fluctuating energy demands: the ‘phosphocreatine circuit’ for cellular energy homeostasis. Biochem. J. 281, 21-40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weatherley A. H., Gill H. S. (1987). Chapter 5, tissues and growth. In The Biology of Fish Growth, pp. 147-175 London: Academic Press; [Google Scholar]
- Weibel E. R., Hoppeler H. (2004). Modeling design and functional integration in the oxygen and fuel pathways to working muscle. Cardiovasc. Eng. 4, 5-18 [Google Scholar]
- Weisz P. B. (1973). Diffusion and chemical transformation. Science 179, 433-440 [DOI] [PubMed] [Google Scholar]
- Wheatley D. N. (2003). Diffusion, perfusion and the exclusion principles in the structural and functional organization of the living cell: reappraisal of the properties of the ‘ground substance’. J. Exp. Biol. 206, 1955-1961 [DOI] [PubMed] [Google Scholar]
- Wittenberg J. B. (1959). Oxygen transport – a new function proposed for myoglobin. Biol. Bull. 117, 402-403 [Google Scholar]
- Wittenberg J. B., Wittenberg B. A. (2003). Myoglobin function reassessed. J. Exp. Biol. 206, 2011-2020 [DOI] [PubMed] [Google Scholar]
- Yoshizaki K., Seo Y., Nishikawa H., Morimoto T. (1982). Application of pulsed-gradient 31P NMR on frog muscle to measure the diffusion rates of phosphorus compounds in cells. Biophys. J. 38, 209-211 [DOI] [PMC free article] [PubMed] [Google Scholar]