CNVnator: An approach to discover, genotype, and characterize typical and atypical CNVs from family and population genome sequencing (original) (raw)

Abstract

Copy number variation (CNV) in the genome is a complex phenomenon, and not completely understood. We have developed a method, CNVnator, for CNV discovery and genotyping from read-depth (RD) analysis of personal genome sequencing. Our method is based on combining the established mean-shift approach with additional refinements (multiple-bandwidth partitioning and GC correction) to broaden the range of discovered CNVs. We calibrated CNVnator using the extensive validation performed by the 1000 Genomes Project. Because of this, we could use CNVnator for CNV discovery and genotyping in a population and characterization of atypical CNVs, such as de novo and multi-allelic events. Overall, for CNVs accessible by RD, CNVnator has high sensitivity (86%–96%), low false-discovery rate (3%–20%), high genotyping accuracy (93%–95%), and high resolution in breakpoint discovery (<200 bp in 90% of cases with high sequencing coverage). Furthermore, CNVnator is complementary in a straightforward way to split-read and read-pair approaches: It misses CNVs created by retrotransposable elements, but more than half of the validated CNVs that it identifies are not detected by split-read or read-pair. By genotyping CNVs in the CEPH, Yoruba, and Chinese-Japanese populations, we estimated that at least 11% of all CNV loci involve complex, multi-allelic events, a considerably higher estimate than reported earlier. Moreover, among these events, we observed cases with allele distribution strongly deviating from Hardy-Weinberg equilibrium, possibly implying selection on certain complex loci. Finally, by combining discovery and genotyping, we identified six potential de novo CNVs in two family trios.

Genomic structural variations (SVs), including copy number (CN) variations (CNVs), are believed to contribute significantly to variations between human individuals and may have as large an effect on human phenotype as do SNPs (Feuk et al. 2006; Sharp et al. 2006). Originally, CNVs were detected from the analysis of SNP and CGH array data (Carter 2007), and this is still a cost-effective method for CNV discovery and genotyping (Conrad et al. 2009). However, new sequencing-based approaches such as clone-based sequencing (Kidd et al. 2008), paired-end mapping (Korbel et al. 2007, 2009), split-read (SR) mapping (Mills et al. 2006), read-depth (RD) analysis (Bentley et al. 2008; Campbell et al. 2008; Alkan et al. 2009; Chiang et al. 2009; Yoon et al. 2009), and integrative methods (Medvedev et al. 2010) offer a valuable alternative as they enable the discovery of more CNVs of all types (inversions and translocations that are not seen by CGH) and sizes (including indels). The great advantage of sequencing-based approaches is that, as shown below, they complement each other and can all be applied to one set of sequencing data (for example, whole-genome paired-end sequencing by Illumina) to yield a comprehensive map of genomic variations, including SNPs.

Here we present a novel method, CNVnator, to detect CNVs from a statistical analysis of mapping density, i.e., RD, of short reads from next-generation sequencing platforms. Previous approaches using RD were limited to only unique regions of the genome (Bentley et al. 2008; Campbell et al. 2008; Chiang et al. 2009), discovered only large CNVs with poor breakpoint resolution (Bentley et al. 2008; Campbell et al. 2008; Alkan et al. 2009; Chiang et al. 2009), or could not perform genotyping (Yoon et al. 2009). CNVnator is able to discover CNVs in a vast range of sizes, from a few hundred bases to megabases in length, in the whole genome. By using data from the 1000 Genomes Project (Durbin et al. 2010), we have experimentally verified CNVnator's ability for sensitive, specific, and precise CNV discovery and genotyping, as well as demonstrated its ability for de novo CNV detection.

Results

Partitioning of the RD signal with the mean-shift approach

For the calculation of the RD signal, CNVnator divides the whole genome into nonoverlapping bins of equal size and uses the count of mapped reads within each bin as the RD signal. It then partitions the generated signal into segments with presumably different underlying CNs. Putative CNVs are predicted by applying statistical significance tests to the segments. All details about the method are given in the Methods section, and here we stress its key features. Partitioning is based on a mean-shift technique originally developed in computer science for image processing (Wand and Jones 1995; Comaniciu and Meer 2002) and applied previously to the analysis of CGH data (Wang et al. 2009). Although it is similar to the analysis of the CGH signal, the analysis of the RD signal has different challenges. In contrast to the CGH signal, in which the locations and intensities of each probe are fixed, for the RD signal, each location can be calculated differently by varying the bin size used to count mapped reads. We have performed a sensitivity analysis to determine an optimal bin size for RD analysis (see Supplemental material). Another factor affecting CNV discovery is the choice of bandwidth for signal partitioning using the mean-shift approach. We developed and applied a novel multiple bandwidth partitioning strategy, which allowed us to detect CNVs across a vast range of sizes, from a few hundred to mega bases in length. Furthermore, the method for RD analysis should be fast. At a sequencing depth of 4×, which is not very deep, the method should be applicable to roughly 10 million data points (assuming bins of 300 bp) and 1000 individuals, as, for example, in the 1000 Genomes Project. The efficient implementation of CNVnator allowed us (given mapped reads) to perform whole-genome analysis within a few hours on a single 2.5-GHz Intel Core 2 Duo CPU.

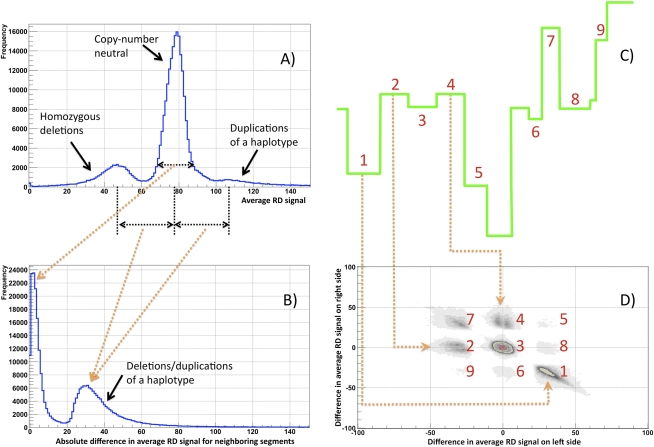
As a first step to assess the performance of our method, we analyzed the partitioning of the entire genome from a statistical point of view using data from the 1000 Genomes Project for one individual (NA12878, the child in the CEPH trio). A distribution of the average RD signal for calculated segments was nonuniform and shows clear differentiation between CN-neutral regions and heterozygous deletions and duplications of one haplotype (Fig. 1A). Note that not all partitioned regions with abnormal RD are called as CNVs by the statistical significance test. Therefore, the area under each peak is not representative of the corresponding fraction of CNVs. Further, either neighboring segments have similar average RD signals (peak around zero in Fig. 1B) or their average signal difference is circa half of the genomic average RD signal (second peak in Fig. 1B). Remarkably, changes in average RD signal at two neighboring segment boundaries cluster, and these clusters can be explained by partitioning that includes deletions and duplications (see Fig. 1C,D). Of particular concern are segments with almost the same average RD signal. These include those segments contributing to the peak around zero in Fig. 1B and cluster 3 in Fig. 1D. We found that these segments are almost exclusively CN neutral (see Methods; Supplemental Fig. S1) and represent variations in average RD due to partitioning with small (relative to their size) bandwidth. Therefore, this analysis suggests proper partitioning of the entire genome into segments of different CNs.

Figure 1.

Statistics on partitioning the RD signal for a child in a CEPH trio (NA12878) using 100-bp bins and standard parameters (see Methods). (A) Average RD signal distribution in produced segments. The distribution has three clear peaks: around the genomic RD average (no CNVs), half of that (heterozygous deletion), and one and one-half of that (duplication of one haplotype). The average genomic RD signal is ∼ 77 reads. Not all partitioned regions with abnormal RD are called CNVs by the statistical significance test. Therefore, the area under each peak is not representative of the corresponding fraction of CNVs. (B) Distribution of the average RD signal difference for neighboring segments. The distribution is for the absolute value of the difference and shows that either produced segments have similar average signals (peak around zero) or their average signals are approximately half of the genomic average RD signal (second peak), indicating deletion/duplication of one haplotype. (C) Example of partitioning clarifying clusters in D. (D) Distribution of the average RD signal difference at the left and right boundary for each segment. The distribution has several clear clusters. Clusters originate due to various combinations of segments with different RD signals. Clusters 8 and 9 represent cases of enclosed events, such as duplication of a region within duplication.

Understanding and filtering CNV calls

Calling a CNV in particular regions is confounded by the presence of the same (or very similar) copies of that region in the reference genome. The RD signal for a CNV in these regions is effectively smeared (due to random placement of nonuniquely mapped reads) over all copies and may be undetectable (e.g., retrotransposons) or give rise to multiple CNV calls at the location of each copy (e.g., segmental duplications). To get more intuition on the latter case, consider the situation in which the reference genome has two almost identical segmental duplications A and B, but only region A is present in the studied sample. Because of diploidy, the studied sample will have A twice (i.e., AA), while the monoploid reference genome will have each region once (i.e., AB). Reads that originate from A in the sample will distribute equally between A and B in the reference, generating half of the average RD (i.e., CN = 1). Consequently, A and B will be identified as deletions. Moreover, the location of the variation is uncertain (it could either be A or B), and this could mislead validation (e.g., by PCR), bias CNV concordance estimation between samples, and cause confusion during downstream analysis. Thus, we developed a procedure to flag (but not eliminate) such potential calls, the q0 filter.

Each mapped read (pair of reads) has an associated mapping quality, which is a measure of the confidence that a read actually comes from the position to which it is aligned (Li et al. 2008a). The larger the value, the greater is the confidence. When a read (pair of reads) can map to two or more locations, then one is randomly chosen. In such cases, the associated mapping quality is zero, hence the name q0 filter. We found that the distribution of the fraction of q0 reads in the called CNV regions segregates around 0 and 100% (see Supplemental Fig. S2). Thus, we consider the CNV region redundant if the fraction of q0 reads in the called CNV regions is >50%. Below we analyze both filtered and unfiltered calls.

Sensitive and precise CNV discovery in trios

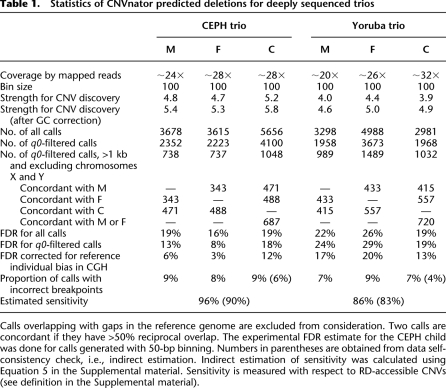
We have applied CNVnator to the analysis of the deeply sequenced (>20×) CEPH and Yoruba trios that were sequenced as a part of the 1000 Genomes Project. Each trio consisted of three individuals/samples: father, mother, and daughter sequenced with paired reads by the Illumina platform (see Table 1). In general, trio analysis is useful in allowing testing for result reproducibility, i.e., all variants in the child should also be found in the parents, and also there must be more shared variants between the child and one of its parents than between parents. For uniformity, we used 100-bp bins to calculate the RD signal for all individuals. Three to five thousand CNV calls were produced for each individual, ranging in size from 200–1,590,400 bp (see Supplemental Fig. S3). From the statistics, one would expect that deeper sequencing would allow for more sensitive and precise CNV detection. Indeed, we observed that the overall strength to discover CNVs, measured as the ratio of the mean to sigma of the Gaussian fit of the RD distribution, correlates with sequencing coverage. However, the uniformity of coverage across the genome is also of extreme importance. The genome of the Yoruba child is sequenced at the highest depth; however, these data allow for the least strength in CNV detection due to the large variance of the RD signal (see Supplemental Fig. S4). In fact, the number of CNV calls made for this person is the smallest of all the data sets.

Table 1.

Statistics of CNVnator predicted deletions for deeply sequenced trios

We have intersected calls that are >1 kb (these events are detected at maximum sensitivity) from the whole genome excluding the X and Y chromosomes, and consider two calls concordant if they have >50% reciprocal overlap. For the CEPH trio, as expected, there are more concordant calls between each parent and the child than between parents. For the Yoruba trio, there is one exception, the call concordance between parents is better than that between mother and child. However, this can be explained by the poorer data quality for the child resulting in an overall smaller number of calls and an overall higher FDR (see below). Additionally, the majority of the CNV calls in children, i.e., 66% for the CEPH child and 70% for the Yoruba child, is concordant with CNV calls from either parent, again in agreement with the expectation.

Validation of calls within the 1000 Genomes Project using CGH arrays with 42 million probes estimated a false-discovery rate (FDR) of ∼13% for the CEPH trio and ∼24% for the Yoruba trio (for _q0_-filtered calls). This validation using CGH arrays is comparative in nature, where probe intensities in one individual (the studied one) are compared with the probe intensities in the reference individual (NA10851). Therefore, validation is biased in the CN variable (with respect to the reference genome) regions of NA10851 (Park et al. 2010). When corrected for this bias (see Supplemental material), the FDR became ∼7% and ∼16% accordingly; i.e., reference individual bias was ∼45% for CEPH and ∼33% for the Yoruba trios. This result matches the expectation that the bias is larger for the CEPH trio, as the array reference individual (NA10851) is also CEPH.

Imperfect call concordance is due to the following three reasons: (1) false positives in CNV calling, (2) false negatives in CNV calling, and (3) an error in CNV breakpoints (i.e., when there is a call in the CNV region, but its breakpoints do not match up) (see Supplemental Fig. S5). The false-positive rate can be obtained from validation experiments, and the other two quantities can be directly estimated from comparison with known CNVs, e.g., discovered by analysis of CGH arrays (Conrad et al. 2009). A priori, it is not obvious that direct estimation can be trusted due to possible different and unknown ascertainment biases of RD analysis and CGH experiments. Therefore, we additionally performed indirect estimations by comparing call consistency in parents and child (a data self-consistency check). We have developed a mathematical model to perform such indirect estimations (see Supplemental material). In short, rules of inheritance allow relating the number of concordant calls for a child and his/her parents with the number of concordant calls between parents and the number of calls in each parent. That leads to excluding the unknown number of CNVs for each trio member from the derivation and relating sensitivity of CNV calling to FDR and the proportion of calls with incorrect breakpoints in a set of equations. For a more intuitive understanding, consider an arbitrary triangle. The sum of all its angles is 180°, independent of the length of its sides. Therefore, if two angles are known, the third can be deduced. Similarly, the sensitivity, FDR, and breakpoint precision in CNV calling can be related (like angles) to the measured call concordance without knowing the number of CNVs (i.e., side lengths in a triangle) for each trio member. By using this model, the sensitivity of CNV discovery can be estimated if the other two values are known.

First, as mentioned above, the fraction of calls with incorrect breakpoints can be estimated directly by comparison with array CGH (aCGH) calls (see Supplemental material). Alternatively, it can be measured indirectly as the fraction of calls in the child that overlaps by at least 1 bp with any call from either parent but is not concordant with any call. Next, using Equation 5 from the Supplement, we indirectly estimated the average sensitivity of CNV discovery (see Supplemental Table S1; numbers in parenthesis in Table 1). The numbers for both quantities, from direct and indirect estimation, agree reasonably well, suggesting that our model correctly describes the CNV inheritance and the process of their discovery. Lower estimation of the sensitivity by indirect measure may imply an ascertainment bias of the CGH array (i.e., bias toward events that are easier to discover) or inaccuracy of some assumptions (i.e., of equal sensitivity) when deriving Equation 5 in the Supplement. Additionally, we performed data-driven simulation for male individuals in each trio and observed similar sensitivity (see Supplemental Fig. S6). Finally, we visually inspected (see Supplemental Table S2) deletions predicted by Conrad but not found by CNVnator in a CEPH child (total of 35 regions). In 11 (32%) cases, CNVnator did not partition a region correctly or did not call it as a CNV. For the remaining 24 (78%) cases, no deviation of the RD signal from the genomic average was observed. Since read mapping in these regions is mostly reliable (only four regions do not pass q0 filter), we concluded that most of them are not CNVs and discordance between CGH and RD experiments can be explained by false CNV discovery and genotyping, ∼15%, in CGH (Conrad et al. 2009). Overall, CNVnator demonstrates a high sensitivity of CNV discovery, low FDR, and a low rate of incorrect breakpoint assignment.

Discovering duplications (compared to deletions) by the mean of the RD represents a greater discovery challenge for several reasons. First, mismapping in repeats can look like a duplication. Second, reads that originate from genomic regions that are not in the reference (i.e., gaps) will map to the homologous regions, e.g., centromeres, telomeres, and gap adjacent regions, producing a larger than normal RD signal. This produces an abnormally high RD signal (see Supplemental Fig. S7) that does not necessarily represent a true duplication but rather the effect of an “unknown reference.” Indeed, we see ∼50% of duplications found by CNVnator are located within 1 Mb from gaps in the reference genome. Last, duplicated regions have a larger RD signal and also larger signal variance. Consequently, we observed a lower sensitivity of ∼85% for duplication discovery (see Supplemental Table S3).

High resolution of breakpoints

Comparison of predicted deletion breakpoints by CNVnator with those identified by SR analysis in the 1000 Genomes Project (Mills 2010), i.e., at base pair resolution, revealed excellent precision of 200 bp for 90% of the breakpoints predicted by CNVnator (see Supplemental Fig. S8), which corresponds to the size of the two bins in which a genome is partitioned. Given the approximate CNV breakpoints, a local assembly of a haplotype bridging an SV region could be accomplished (Huang et al. 1993; Leary et al. 2010; Slade et al. 2010). Subsequently, alignment of the assembled contig to the predicted CNV region can identify precise CNV breakpoints (Abyzov and Gerstein 2010).

Naturally, precision in breakpoint location is a function of bin size, which is also a lower theoretical limit on breakpoint resolution. CNVnator is very close to that limit. Also, note that the choice of bin size is a function of coverage, read length, and data quality. Thus, for constant read length and data quality, breakpoint localization precision would increase with sequencing coverage. Specifically, given the same data quality and read length, we observed that the optimal bin size, and thus breakpoint resolution accuracy, scales roughly inversely with the coverage, resulting in ∼100-bp bins for 20–30× coverage, ∼500-bp bins for 4–6× coverage, and ∼30-bp bins for ∼100× coverage. However, in the last case, bin size is comparable to read length (∼36 for the data used in this study), and this can compromise breakpoint resolution due to unreliable read mapping around CNV breakpoints.

Single-genome genotyping

We have developed a procedure for CNV genotyping, i.e., for assigning CN to a given genomic region by calculating its RD signal normalized to the genomic average for the region of the same length:

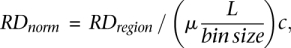
where RDregion is the RD signal for a given region of length L, μ is the mean of a Gaussian best fit to the distribution of the RD signal for bins of a given size (see Supplemental Fig. S9), and c is a scaling factor equal to 2 for all chromosomes except X and Y in male individuals, where c is equal to 1. Such normalization is prone to outliers, i.e., bins containing repeats with an abnormal amount of mapped reads or bins in gaps of the reference genome where no reads map. The RD signal for a region can be calculated by summing the RD signal in bins covering the region. Additionally, note that one can use an arbitrary (not the same as for calculating RDregion) bin size for normalization, although it should be sufficiently large to allow for a reliable estimation of μ.

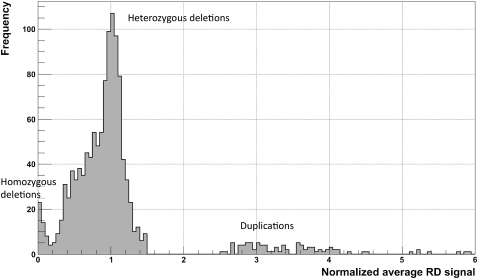
The distribution of the normalized average RD signal in the CNVnator-predicted regions is multimodal with two distinct peaks corresponding to homo- and heterozygous deletions and a less distinct cluster corresponding to duplications (see Fig. 2). Smeared peaks for duplications are reflective of the larger variance for the larger RD signal. We assigned a CN to a genomic region by rounding off its normalized average RD signal to the nearest integer. With this strategy, we obtained the same CN for 95% and 93% of RD-accessible (see definition in Supplemental material) deletions as CN genotyped by two array-based analyses (McCarroll et al. 2008; Conrad et al. 2009). It is worth noting that RD achieves high accuracy but still employs a smaller amount of information, i.e., sequencing from single individuals, while other approaches mentioned above genotype CNVs by analyzing probe intensities for multiple (hundreds) individuals. We observed even higher concordance of 98% in genotyping when comparing to the smaller but experimentally measured and highly confident genotype set (27 regions) (see Supplemental material; Supplemental Table S4).

Figure 2.

Distribution of normalized average RD signal for predicted CNVs (for a CEPH daughter) that are >1 kb and pass the q0 filter. The normalization factor is the double (two copies of each chromosome) of the genome-wide average RD signal. Two clear peaks (around 0 and 1) correspond to homozygous and heterozygous deletions. Slight displacement of the second peak (∼0.05) from a value of 1 is the result of read over-mapping in those regions, when choosing a mapping location for nonuniquely mapped reads (see Methods). Peaks for duplications are smeared, which reflects the larger variations in the RD signal and, as a consequence, the greater challenge in detecting and genotyping duplications.

By using the same approach, we were able to genotype low CN (CN of 3–4) duplications. Namely, we obtained the same CN for 48% and 84% of RD-accessible duplications in the same two sets. The lower agreement between RD and array genotyping probably reflects the fact that the discovery and genotyping of duplications is generally a harder problem. Furthermore, the population genotyping approach using arrays can be misled in determining the absolute CN as the range of log2 ratios for high-frequency duplications is expected to overlap in the range of low frequency deletions, e.g., rare and de novo events (Conrad et al. 2010). In other words, duplications and rare deletions are easier to be misgenotyped when using CGH.

We found that varying the cutoff for normalized RD signals to assign CN, e.g., using 0.75 to differentiate homozygous deletions from heterozygous ones, enables a better agreement with array genotyping. However, the improvement is marginal, on the order of 1%. We also applied our genotyping strategy to individuals sequenced with low coverage (1–6×) using 1-kb bins to calculate normalization. While overall concordance with CGH-based genotypes (Conrad et al. 2009) was the same as for deeply sequenced individuals, we noticed a few samples with low concordance that can be explained by low coverage and problems with data quality. Therefore, we excluded the following individuals from our subsequent analysis: NA18532, NA19210, NA18555, NA18562, NA12005, NA18486, NA12892, and NA18571.

Comparison with other approaches for CNV discovery

Other approaches and methods for CNV discovery from sequencing data, i.e., read-pair (RP) and SR, were employed on the same data in the framework of the 1000 Genomes Project, allowing their direct comparison (Mills 2010). Out of the RD-based methods, CNVnator demonstrated the highest sensitivity, the lowest FDR, and the most precise breakpoint resolution (see Supplemental Table S5). Different approaches were also found to be complementary and not directly comparable, a suggestion made earlier (Yoon et al. 2009), with each approach uniquely discovering ∼30%–60% of the CNVs. In fact, >50% of the CNVs found by CNVnator and validated by CGH array are not detected by SR and RP approaches.

The effectiveness of each approach for CNV discovery is a complex function of read length, sequencing coverage, and average span between read pairs. However, if applied to the same data, read mapping is the key factor when evaluating the advantage of a particular approach. For instance, if a repetitive/duplicated region on either side flanks a CNV, then the CNV can be missed by RP or SR approaches due to ambiguous mapping of at least one read (or read end for SR), i.e., due to relying on the independent mapping of each read/end. However, for RD analysis, one can restrain reads to map in the proper orientation within a certain distance defined by the average span between reads and thus effectively require that only one read maps unambiguously. In fact, it can be shown mathematically that RD analysis can better ascertain a CNV in segmental duplications, i.e., low CN repeats, than can RP analysis (see Supplemental material). On the other hand, if a CNV is a repeat but flanking sequences are not (e.g., retrotransposon), then it is more likely to be found by RP and missed by RD approaches. Indeed, judging from the intersection with 58 deletions (known with breakpoint resolution) for the CEPH child (Kidd et al. 2008), CNVnator mostly misses (see Supplemental Table S4) CNVs consisting entirely of a single retrotransposon (LINE, SVA, or HERV-K). Additionally, simply because of its nature, RD analysis cannot discover balanced (i.e., those not changing CN) SVs that can be found by RP- and SR-based methods.

Apart from that, CNVnator can discover and genotype both deletions and duplications, while methods for deletion genotyping by RP and SR approaches are immature and perspectives for duplication genotyping are unclear. Finally, RD genotyping can be easily applied to low coverage data and still yield precise results as we demonstrated above. From these arguments, we reason that CNVnator is uniquely suited for analyses requiring CNV discovery and comparison (except for retrotransposons) of CN across few/several individuals or even an entire population, such as de novo and multi-allelic CNV analysis.

Detecting atypical CNVs

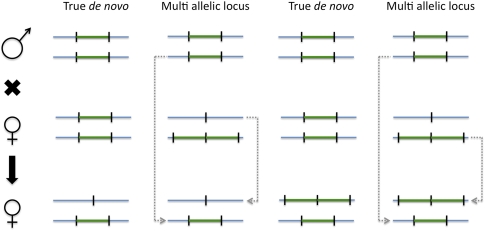
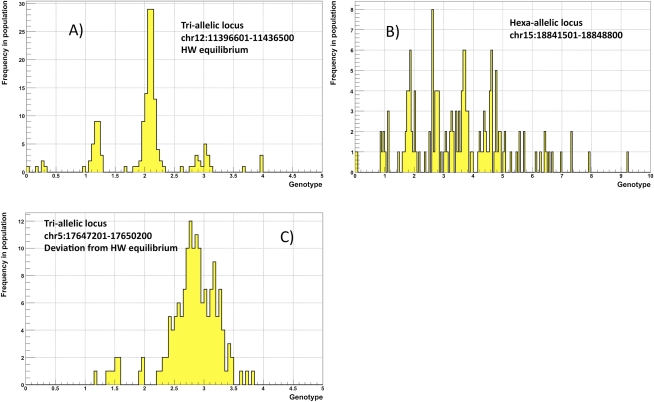
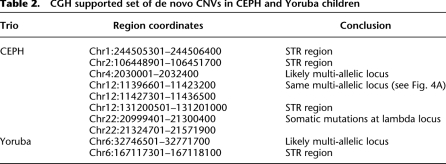
The combination of discovery and genotyping techniques employed by CNVnator can be used to classify CNVs as atypical such as de novo and multi-allelic. De novo CNVs can be found by identifying child-specific CNVs, i.e., those not found in parents. However, such de novo CNV candidates can also be explained by multi-allelic loci (Fig. 3) having at least three different alleles, e.g., CN0, CN1, and CN2, in a population. By using sequencing data for a population of 161 individuals in the 1000 Genome Project, we estimated that the frequency of such CNVs is 11%–13% (see Supplemental material). For putative multi-allelic loci, we observed cases with an allele distribution deviating from Hardy-Weinberg equilibrium, possibly implying strong selection on certain complex loci (Fig. 4). For instance, genotype values for the locus at chr5:17647201–17650200 (see Fig. 4C) range from 1.2 to 3.8, suggesting that alleles can have from zero to two copies of the regions, i.e., CN0, CN1, and CN2. However, predominantly, the locus has three copies, suggesting dominance of CN1 and CN2 alleles in similar quantities in the population, i.e., balancing selection.

Figure 3.

When analyzing family trios, multi-allelic loci can look like de novo CNVs.

Figure 4.

Examples of multi-allelic loci. (A) Tri-allelic locus with CN0, CN1, and CN2 is at Hardy-Weinberg equilibrium. (B) Distribution of genotypes across a population can be explained by hexa-allelic locus with CN0–CN5. (C) Tri-allelic locus that is not at Hardy-Weinberg equilibrium, which may indicate natural selection. In this case, the distribution of genotypes peaks around 3, with the likely explanation that an equal proportion of CN1 and CN2 alleles at this locus dominate the population. This, in turn, implies balancing selection.

To find de novo CNVs, we did the following: For each trio, we genotyped across all members the _q0_-filtered CNV calls made for the child. We selected putative de novo candidates that satisfied the following criteria: (1) The normalized RD signal in the child is less than 1.4 (more than 2.6 for duplications); and (2) the normalized average RD signal in each parent is more than 1.6 (less than 2.4 for duplications). Although 1.5 is the cutoff to discriminate between heterozygous deletions and the normal diploid state, we note that genotyping estimation can be biased by ∼0.05 (see Fig. 2), and thus we made the cutoff more stringent by subtracting/adding the double (0.1) of the value. In the same way we made a more stringent cutoff to detect de novo duplications. This approach predicts 17 and six, with a total of 23, child-specific CNVs for the CEPH and Yoruba trios, respectively. We gain additional support for the predictions using a high probe density (∼42 million) CGH array with hybridization done for each trio member (see Supplemental material). We found a total of 10 potential de novo deletions: two from the CEPH trio and eight from the Yoruba trio. We further inspected each one of them (Table 2).

Table 2.

CGH supported set of de novo CNVs in CEPH and Yoruba children

Judging from genotyping in a population, four events are likely to be multi-allelic loci. Two more are found at the immunoglobulin lambda locus and are thus likely to be somatic, as sequencing and array analysis was done on lymphoblastoid cell lines. The remaining four are found in simple tandem repeats (STRs) regions and may be false positives (due to a read mapping problem for RD analysis and cross-hybridization for arrays) or suggest a repeat extension (germline or somatic) in those regions. Additional validation, e.g., by PCR, is required to reach a definitive answer. Thus, no confident de novo CNVs other than at the lambda locus were detected, but this may not be surprising as they are thought to be found in only one of eight to 50 newborns (Lupski 2007).

Discussion

We have developed and described a novel method, CNVnator, for CNV discovery from statistical analysis of read mapping density, i.e., read depth, that can be applied to single-end and paired-end data from different sequencing platforms such as Illumina, SOLiD, and Helicos (see also Supplemental material). It can also be applicable for CNV discovery at low sequencing coverage (see Supplemental material). Extensive validation and comparison with known CNVs revealed that CNVnator is a sensitive and specific method of CNV discovery and genotyping with high fidelity breakpoint localization. The software is freely available at http://sv.gersteinlab.org/cnvnator and can be applied to various human and nonhuman genomes (genome description is parsed from SAM/BAM file header).

As we pointed out, RD analysis has limitations with respect to detection of balanced CNVs and CNVs created by transposable elements. However, we reasoned that this approach is still suited for analyses requiring the comparison of CN across a few/several individuals or even an entire population. The example of the former analysis is the discovery of de novo CNVs, while the latter one is the identification of atypical, i.e., multi-allelic, CNVs. By using CNVnator, we identified six potential de novo CNVs in two family trios and provide an estimate that multi-allelic loci constitute at least 11% of large CNVs. This estimate is considerably higher than the 7% reported in a previous study (Conrad et al. 2009) using CGH. However, note that Conrad et al. (2009) made clear their difficulty in genotyping multi-allelic events. We, thus, can see their result as being consistent with ours within the bounds of error.

An interesting question is the origin of multi-allelic loci. Since loci with CN0, CN1, and CN2 alleles dominate, the chromosomal crossover at homologous but not equivalent sequences seems to be the most parsimonious explanation: Once two chromosomes recombine, two new alleles, CN0 and CN2, are generated, both of which propagate into the population. Generation of other alleles, i.e., CN3 or larger, may involve two or more chromosomal crossovers.

In the case of tri-allelic loci implying only one crossover event, one would not expect an equal proportion of CN0 and CN2 alleles in the population, as the proportion could be different already at the following (after the individual harboring crossover) generation due to a limited number of offspring. Successive crossover events at the loci can furthermore change allele frequencies. Additionally or alternatively, allele frequencies can be shaped by natural selection, for which we saw evidence (Fig. 4). Thus, one can expect that the frequencies of deletion and duplication alleles could be different, maybe even drastically; e.g., either allele is extremely rare or missing. In light of this, it seems possible that the analysis of a larger population, as, e.g., in the main phase of the 1000 Genomes Project, will result in an even higher estimation of the fraction of the multi-allelic loci due to discovering rare duplication/deletion in the loci of common deletion/duplication.

It was observed previously and shown here that the RD, RP, and SR approaches are complementary. Rapid advances in sequencing technologies, i.e., decreasing cost of sequencing and increasing read length, bring an important question of how RD analysis is affected by the changing data. While careful analysis is yet to be done, it is clear that at constant coverage, sequencing with longer reads diminishes sensitivity to smaller CNVs as less reads are generated. This can be partially compensated by the better read mapping, which also enlarges the fraction of RD-accessible genome, i.e., where reads map unambiguously, potentially bridging the disagreement in CNV discovery with RP and SR approaches. It is tempting to suggest increasing sequencing coverage proportionally with the increase in read length as an optimal strategy to strengthen RD analysis. However, with no SR mappings allowed (a widely adopted mapping strategy), longer reads lengthen the uncertainty in mapping around CNV breakpoints, with the uncertainty being proportional to the read length. In other words, fundamentally breakpoint precision and, thus, ability for precise discovery of small CNVs by RD analysis would degrade with the increased read length, regardless of coverage. Therefore, it seems likely that with longer reads and high coverage, RD analysis will still need to be complemented by other approaches for CNV discovery.

Methods

Read placement

Most short reads (even 30 nucleotides in length) can be uniquely placed (Rozowsky et al. 2009) onto the human genome. However, read placement may be challenging for reads that originate from repetitive regions or regions of segmental duplication. These reads can be aligned to multiple locations in the genome with equal (or almost equal) scores. One way of handling this is to simply exclude such unmappable genomic regions from consideration (Chiang et al. 2009), thus limiting the score of CNV discovery. Another, more common approach (Li et al. 2008a,b; Langmead et al. 2009) is to place a read to a random location out of many where a read aligns with similar scores. We have adopted the latter one for single-end sequencing data.

For paired-end data, where the sequenced reads are the ends of the same DNA fragment, one can use extra information to improve read placement. Namely, most of the time, except ends spanning CNVs, ends should map in proper orientation within a certain distance defined by the average span between ends. In case of ambiguous end placements, using this extra information allows us to discard unlikely read placements. If a pair of reads still cannot be placed uniquely, then, as for single reads, one random location is chosen. This strategy was used in the 1000 Genomes Project for mapping paired-end reads with MAQ (Li et al. 2008a).

We used such a strategy, as opposed to using uniquely mapped reads, to get the uniform depth of coverage across genome (see Supplemental Fig. S9) as it is essential for signal partitioning and CNV calling. When used with uniquely mapped reads, CNVnator calls for 10-fold more deletion and threefold less duplication, suggesting that the results are unreliable.

RD signal calculation and correction of GC-bias

The data used in this analysis were generated with the Illumina sequencing platform (Bentley et al. 2008). Most of the reads were 36 bp in length. To calculate the RD signal, we have divided the entire human genome into consecutive nonoverlapping bins of equal size. We then calculated the RD signal for each bin as a number of placed reads with centers within bin boundaries. As in aCGH experiments (Marioni et al. 2007) and other studies involving Illumina sequencing, we observed a correlation of RD signal and GC content of the underlying genomic sequence (see Supplemental Fig. S10). Similar to another study (Yoon et al. 2009), we corrected this bias by utilizing the following equation:

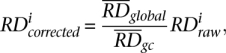
where i is bin index, 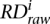is raw RD signal for a bin, 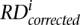is corrected RD signal for the bin, 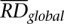is average RD signal over all bins, and 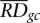is the average RD signal over all bins with the same GC content as in the bin. Such correction effectively eliminates correlation of RD signal with GC content (see Supplemental Fig. S10).

Mean-shift technique

The partitioning procedure is based on an image processing technique (Wand and Jones 1995; Comaniciu and Meer 2002; Wang et al. 2009) known as mean-shift theory. A diagram of the RD signal across genome/chromosome (see Supplemental Fig. S2) can be thought of as an image that needs to be processed with the aim of identifying different genomic CN regions. Statistically, we can formulate this problem as finding a probability distribution function (PDF) from the observed RD data, where the PDF itself is an unknown mixture of many distributions corresponding to each of the CN states. The density maxima in the distribution of intensities are the modes of the PDF, where the gradient of the estimated PDF are zeros. The mean-shift method presents an elegant way to locate these density maxima without having to estimate the density directly (Comaniciu and Meer 2002). The mean-shift process is an iterative procedure that shifts each data point to these density maxima along the mean-shift vector (see Supplemental Fig. S12).

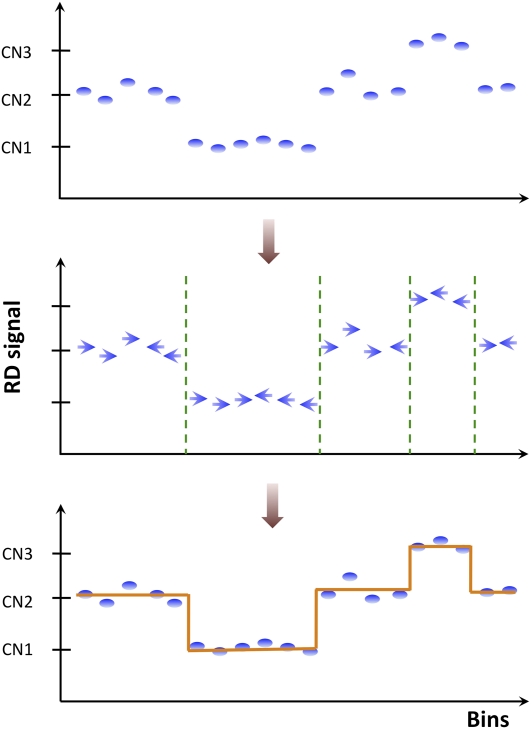
Figure 5 displays a schematic of how mean-shift procedure works for RD data. First, determine a mean-shift vector direction of each point (bin) by comparing its RD signal with neighboring bins (see details below). The vector points in the direction of bins with the most similar RD signal, thus effectively segmenting the RD signal diagram into local modes of attraction. Second, segment breakpoints are determined where two neighboring vectors have opposite direction but do not point to each other. In this regard, breakpoint determination is similar to the edge detection problem in computer vision.

Figure 5.

Schematics of mean-shift procedure. For each bin, i.e., data point, the mean-shift vector points in the direction of bins with the most similar RD signal. Segment breakpoints are determined where two neighboring vectors have opposite directions but do not point to each other.

The mathematical derivation of kernel density estimation theory was described elsewhere (Wand and Jones 1995; Comaniciu and Meer 2002). Here we describe details specific to the analysis of the RD signal. We represent each _i_th bin as a point in two-dimensional space xi = (i,ri), where ri is the RD signal in the bin. Then, assuming independence of the RD signal from the bin index and using the Gaussian kernel, we get the estimation of density function F (x) as

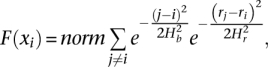
where j is the index of neighboring bins, Hb and Hr are the bandwidths for the bin index and RD signal accordingly, and norm is the normalization factor. The mean-shift vector is a gradient of PDF function and, thus, is also two-dimensional, i.e.,

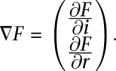
However, the component of the gradient for the RD signal is not of interest as the objective is to segment the genome rather than the signal. We, therefore, derive equations to calculate the component of gradient along the genome dimension only:

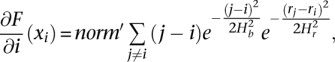
where _norm_′ is the normalization factor for the mean-shift vector. _norm_′ is always positive and thus only affects the component magnitude but not the direction. We are interested in the direction of the vector only and omit calculations of _norm_′. Once the vector is calculated for each bin, boundaries of genomic segments are identified by finding consecutive pairs of bins with mean-shift vectors switching direction from left to right (see Fig. 5). Then, smoothing of the RD signal is performed by averaging signal values within each segment.

Note, mean-shift technique does not require prior knowledge of the number of segments or assumptions about probability distributions. This approach performs the discontinuity preserving smoothing on the RD signal through kernel density estimation and the mean-shift computation. The result is a set of regions with different underlying CNs. It is important, however, to understand that the mean-shift technique segments the RD signal locally, and the statistical difference between different segments is significant in the context of the neighborhood used for partitioning. When scaled to the whole genome, such differences may not be statistically significant anymore. Therefore, calling of CNVs given a partitioning map is a separate issue. The following section describes a partitioning algorithm with the mean-shift technique. It is of general purpose and can, in principle, be applied to any linear signal that needs to be partitioned into local segments. The section after describes the procedure to call CNV given a partitioning map.

Partitioning algorithm

An issue in applying the mean-shift technique to data analysis is the choice of the value of the bandwidths. We set the bandwidth for the RD signal, i.e., value of 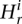, as

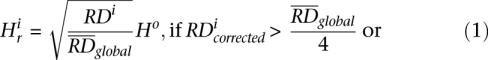
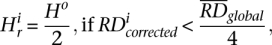
where Ho is an estimate (standard deviation) of global variation in the RD signal obtained by the best fit of the Gaussian function to RD distribution. The second line sets up a lower limit for the bandwidth, because otherwise it could be zero. We have chosen square root scaling of RD bandwidth with the RD signal assuming the Poisson distribution for the signal. However, we observed that RD distribution is overdispersed, consistent with another report (Yoon et al. 2009), but is described well by a Gaussian function (see Supplemental Fig. S9). The standard deviation of the sum of the exact same Gaussians, e.g., two, three, or four copies of the same haplotypes, scales as the square root with the number of summed functions, i.e., with CN. Consequently, it scales as the square root with the mean of the sum of the Gaussians, just like in Equation 1. Therefore, the equation does not need to be revised, and we rely on it in RD signal partitioning.

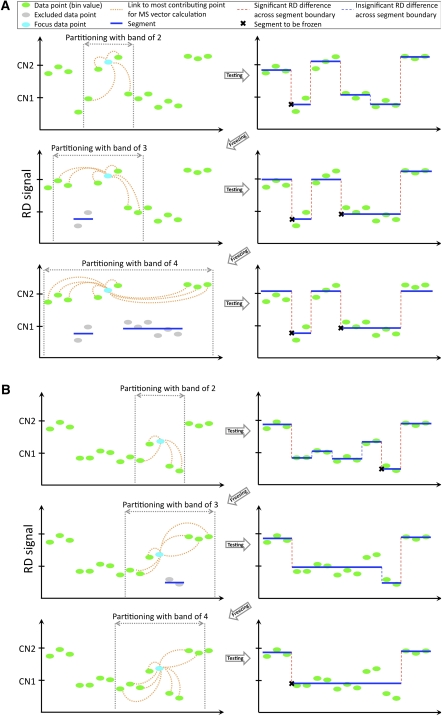
It is not obvious how to choose a bandwidth for the bin index (i.e., Hb), as its meaning is the size of the genomic neighborhood to calculate the mean-shift vector. Using large values will effectively reduce sensitivity to detect small segments (see Supplemental Fig. S13). Using small values makes reconstruction of large CNVs difficult as partitioning may represent local variation of the RD signal and lead to fragmentation of large CNV regions into smaller ones. Besides, at large bandwidth it is difficult to resolve boundaries of colocalized CNVs. We, therefore, developed a novel multistep partitioning strategy with a steady increase of Hb bandwidth and temporarily excluding (“freezing”) from partitioning those segments with the RD signal being significantly different from the one in neighboring segments and the genomic average. At each step, all segments get unfrozen and tested for the possibility (given new partitioning) of being frozen again, allowing for a dynamic region resegmentation as portioning of surrounding regions changes. Partitioning starts and proceeds as described by the following pseudocode and schematically displayed in Figure 6.

Figure 6.

Cartoon demonstration of the adaptive procedure for an increase in bandwidth Hb. (A) When the band is 2, then the largest contribution to mean-shift vector calculations, e.g., for the cyan bin, comes from two neighboring bins. Following the partitioning, two bins within one segment get “frozen,” and bins within it are excluded from partitioning on the next step. New partitioning allows for freezing of more bins that are skipped at the next step when bandwidth equals 4. (B) The deletion region is clearly seen by the eye but could not be detected as a whole at a bandwidth of 2. Only a small portion is detected as CNV and gets “frozen.” After new partitioning with a bandwidth of 3, the region is not frozen anymore and is included for partitioning on the next step (bandwidth of 4), where the complete region of deletion is detected.

• Set Hb to 2
• While bandwidth is less then limit {
• Exclude frozen segments from calculations
• Do 3 times {
• Partition by mean-shift with current bandwidth
• Average RD signal within each segment
• Replace RD values within each segment with the corresponding average
• }
• Add frozen segments to partitioning
• Unfreeze all frozen segments
• Restore original RD values for all points
• For each segment {
• Calculate average and standard deviation of RD signal
• If (segment mean RD is different from genomic average and
• segment mean RD is different from neighboring segments)
• freeze the segment
• }
• Increase bandwidth
• }
• Merge segments
• Make CNV calls

Segment mean RD is different from genomic average if one-sample _t_-test _P_-value is less than 0.05. Two segments have different mean RDs if the two-sample _t_-test _P_-value corrected for multiple hypotheses testing (see CNV calling) is less than 0.01 or means deviate by at least 2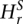, where the index s refers to the segment being tested. The latter heuristic condition is applied only when the segments are shorter than 15 bins, i.e., when e-values can be insignificant due to limited statistics, which is typical when partitioning with small bandwidth. Thus, its primary purpose is to improve sensitivity to small CNV discovery. The condition of 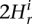represents a reasonable cutoff specifying that average RD signals in segments are different by at least two standard deviations. The step to increase the value of Hb is kept approximately proportional to the value of Hb. Namely, the step is 1 for values up to 8, 2 up to 16, 4 up to 32, 8 up to 64, and 16 up to 128.

Signal merging

We typically stop iterating at Hb = 128, as the RD signal is reasonably smooth by that stage and has three clear peaks (see Supplemental Fig. S1): around average genomic RD (no CNVs), half of that (heterozygous deletion), and one and a half of that (duplication of one haplotype). Further iterations are time-consuming, as computational time is proportional to the value of Hb . We, therefore, merge adjacent segments with minimal difference in average RD by greedy algorithm. Merging stops when the difference is more than a quarter of the genomic average, i.e., half of the difference between means of the RD signal corresponding to two incremental CNs. This cutoff also approximates the bounds of the major peak in mean RD distribution for partitioned segments (see Supplemental Fig. S1). And indeed segment merging mostly affects CN-neutral regions (major peak in the figure). We therefore concluded that refining partitioning by merging neighboring segments is reasonable. However, we stress that it may not need to be applied if partitioning iterations continued until very larger values of Hb.

CNV calling

To call a CNV, we first select segments with a mean RD signal deviating by at least a quarter (half for chromosomes X and Y in male individuals) from the genomic average RD signal. We have chosen this cutoff following the same reason as for segment merging (see above). For each selected segment, we calculated one-sample _t_-test _P_-value of whether the mean of the RD signal within the segment has a value of genomic average, i.e.,

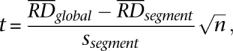
where n is the number of bins within the segment, 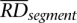is its average RD signal, and ssegment is the signal standard deviation. _P_-values were corrected for multiple hypotheses testing assuming 99% of the whole genome is CN neutral:

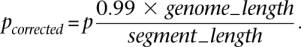
We first call regions with _P_-value by a _t_-test less than 0.05. However, due to statistical fluctuation in read mapping, long CNVs may have regions looking CN neutral. To avoid fragmentation of long CNVs into multiple calls, we merge two calls and the region in between if the means of the RD signal within each call and the region are the same (_P_-value >0.01) by a two-sample _t_-test. In other words, we test for a new hypothesis that the region between two calls is a CNV. The _P_-values were also corrected for multiple hypotheses testing assuming that 1% of the reference genome is CN variable, i.e.,

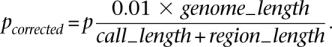
Afterward, we extend our call set by calling additional deletions (corrected _P_-value <0.05) by performing a one-sided test that all values of the RD signal within a segment are smaller than the maximum RD signal within the segment, i.e.,

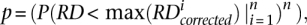
where P is the probability of the RD signal being found in the lower tail of the Gaussian distribution with parameters estimated from the best fit to genome wide RD distribution (see Supplemental Fig. S9), and n is number of bins within the segment. Thus, we have applied more stringent criteria to call for duplications, as those are susceptible to the systematic read mapping bias caused by “unknown reference” (see Results).

Acknowledgments

We acknowledge support from the NIH and from the AL Williams Professorship funds. We also acknowledge the Yale University Biomedical High Performance Computing Center, its support team (in particular, Robert Bjornson and Nicholas Carriero), and NIH grant RR19895, which funded the instrumentation. We thank Ekta Khurana, Xinmeng Jasmine Mu, and Declan Clarke for useful discussions during the course of the study and help in preparing the manuscript.

Footnotes

[Supplemental material is available for this article.]

References

1. Abyzov A, Gerstein M 2011. AGE: Defining breakpoints of genomic structural variants at single-nucleotide resolution, through optimal alignments with gap excision. Bioinformatics 27: 595–603 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Alkan C, Kidd JM, Marques-Bonet T, Aksay G, Antonacci F, Hormozdiari F, Kitzman JO, Baker C, Malig M, Mutlu O, et al. 2009. Personalized copy number and segmental duplication maps using next-generation sequencing. Nat Genet 41: 1061–1067 [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Bentley DR, Balasubramanian S, Swerdlow HP, Smith GP, Milton J, Brown CG, Hall KP, Evers DJ, Barnes CL, Bignell HR, et al. 2008. Accurate whole human genome sequencing using reversible terminator chemistry. Nature 456: 53–59 [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Campbell PJ, Stephens PJ, Pleasance ED, O'Meara S, Li H, Santarius T, Stebbings LA, Leroy C, Edkins S, Hardy C, et al. 2008. Identification of somatically acquired rearrangements in cancer using genome-wide massively parallel paired-end sequencing. Nat Genet 40: 722–729 [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Carter NP 2007. Methods and strategies for analyzing copy number variation using DNA microarrays. Nat Genet 39: S16–S21 [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Chiang DY, Getz G, Jaffe DB, O'Kelly MJ, Zhao X, Carter SL, Russ C, Nusbaum C, Meyerson M, Lander ES 2009. High-resolution mapping of copy-number alterations with massively parallel sequencing. Nat Methods 6: 99–103 [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Comaniciu D, Meer P 2002. Mean shift: A robust approach toward feature space analysis. IEEE Trans Pattern Anal Mach Intell 24: 603–619 [Google Scholar]
8. Conrad DF, Pinto D, Redon R, Feuk L, Gokcumen O, Zhang Y, Aerts J, Andrews TD, Barnes C, Campbell P, et al. 2010. Origins and functional impact of copy number variation in the human genome. Nature 464: 704–712 [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Durbin RM, Abecasis GR, Altshuler DL, Auton A, Brooks LD, Gibbs RA, Hurles ME, McVean GA 2010. A map of human genome variation from population-scale sequencing. Nature 467: 1061–1073 [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Feuk L, Carson AR, Scherer SW 2006. Structural variation in the human genome. Nat Rev Genet 7: 85–97 [DOI] [PubMed] [Google Scholar]
11. Huang W, Sun GL, Li XS, Cao Q, Lu Y, Jang GS, Zhang FQ, Chai JR, Wang ZY, Waxman S, et al. 1993. Acute promyelocytic leukemia: Clinical relevance of two major PML-RAR alpha isoforms and detection of minimal residual disease by retrotranscriptase/polymerase chain reaction to predict relapse. Blood 82: 1264–1269 [PubMed] [Google Scholar]
12. Kidd JM, Cooper GM, Donahue WF, Hayden HS, Sampas N, Graves T, Hansen N, Teague B, Alkan C, Antonacci F, et al. 2008. Mapping and sequencing of structural variation from eight human genomes. Nature 453: 56–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Korbel JO, Urban AE, Affourtit JP, Godwin B, Grubert F, Simons JF, Kim PM, Palejev D, Carriero NJ, Du L, et al. 2007. Paired-end mapping reveals extensive structural variation in the human genome. Science 318: 420–426 [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Korbel JO, Abyzov A, Mu XJ, Carriero N, Cayting P, Zhang Z, Snyder M, Gerstein MB 2009. PEMer: A computational framework with simulation-based error models for inferring genomic structural variants from massive paired-end sequencing data. Genome Biol 10: R23 doi: 10.1186/gb-2009-10-2-r23 [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Langmead B, Trapnell C, Pop M, Salzberg SL 2009. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol 10: R25 doi: 10.1186/gb-2009-10-3-r25 [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Leary RJ, Kinde I, Diehl F, Schmidt K, Clouser C, Duncan C, Antipova A, Lee C, McKernan K, De La Vega FM, et al. 2010. Development of personalized tumor biomarkers using massively parallel sequencing. Sci Transl Med 2, 20ra14 doi: 10.1126/scitranslmed.3000702 [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Li H, Ruan J, Durbin R 2008a. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res 18: 1851–1858 [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Li R, Li Y, Kristiansen K, Wang J 2008b. SOAP: Short oligonucleotide alignment program. Bioinformatics 24: 713–714 [DOI] [PubMed] [Google Scholar]
19. Lupski JR 2007. Genomic rearrangements and sporadic disease. Nat Genet 39: S43–S47 [DOI] [PubMed] [Google Scholar]
20. Marioni JC, Thorne NP, Valsesia A, Fitzgerald T, Redon R, Fiegler H, Andrews TD, Stranger BE, Lynch AG, Dermitzakis ET, et al. 2007. Breaking the waves: Improved detection of copy number variation from microarray-based comparative genomic hybridization. Genome Biol 8: R228 doi: 10.1186/gb-2007-8-10-r228 [DOI] [PMC free article] [PubMed] [Google Scholar]
21. McCarroll SA, Kuruvilla FG, Korn JM, Cawley S, Nemesh J, Wysoker A, Shapero MH, de Bakker PI, Maller JB, Kirby A, et al. 2008. Integrated detection and population-genetic analysis of SNPs and copy number variation. Nat Genet 40: 1166–1174 [DOI] [PubMed] [Google Scholar]
22. Medvedev P, Fiume M, Dzamba M, Smith T, Brudno M 2010. Detecting copy number variation with mated short reads. Genome Res 20: 1613–1622 [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Mills RE, Walter K, Stewart C, Handsaker RE, Chen K, Alkan C, Abyzov A, Yoon SC, Ye K, Cheetham RK, et al. 2011. Mapping copy number variation by population-scale genome sequencing. Nature 470: 59–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Mills RE, Luttig CT, Larkins CE, Beauchamp A, Tsui C, Pittard WS, Devine SE 2006. An initial map of insertion and deletion (INDEL) variation in the human genome. Genome Res 16: 1182–1190 [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Park H, Kim JI, Ju YS, Gokcumen O, Mills RE, Kim S, Lee S, Suh D, Hong D, Kang HP, et al. 2010. Discovery of common Asian copy number variants using integrated high-resolution array CGH and massively parallel DNA sequencing. Nat Genet 42: 400–405 [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Rozowsky J, Euskirchen G, Auerbach RK, Zhang ZD, Gibson T, Bjornson R, Carriero N, Snyder M, Gerstein MB 2009. PeakSeq enables systematic scoring of ChIP-seq experiments relative to controls. Nat Biotechnol 27: 66–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Sharp AJ, Cheng Z, Eichler EE 2006. Structural variation of the human genome. Annu Rev Genomics Hum Genet 7: 407–442 [DOI] [PubMed] [Google Scholar]
28. Slade I, Stephens P, Douglas J, Barker K, Stebbings L, Abbaszadeh F, Pritchard-Jones K, Cole R, Pizer B, Stiller C, et al. 2010. Constitutional translocation breakpoint mapping by genome-wide paired-end sequencing identifies HACE1 as a putative Wilms tumour susceptibility gene. J Med Genet 47: 342–347 [DOI] [PubMed] [Google Scholar]
29. Wand MP, Jones MC 1995. Kernel smoothing 1st edChapman & Hall, New York [Google Scholar]
30. Wang LY, Abyzov A, Korbel JO, Snyder M, Gerstein M 2009. MSB: A mean-shift-based approach for the analysis of structural variation in the genome. Genome Res 19: 106–117 [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Yoon S, Xuan Z, Makarov V, Ye K, Sebat J 2009. Sensitive and accurate detection of copy number variants using read depth of coverage. Genome Res 19: 1586–1592 [DOI] [PMC free article] [PubMed] [Google Scholar]