Accurate Model Selection of Relaxed Molecular Clocks in Bayesian Phylogenetics (original) (raw)
Abstract
Recent implementations of path sampling (PS) and stepping-stone sampling (SS) have been shown to outperform the harmonic mean estimator (HME) and a posterior simulation-based analog of Akaike’s information criterion through Markov chain Monte Carlo (AICM), in Bayesian model selection of demographic and molecular clock models. Almost simultaneously, a Bayesian model averaging approach was developed that avoids conditioning on a single model but averages over a set of relaxed clock models. This approach returns estimates of the posterior probability of each clock model through which one can estimate the Bayes factor in favor of the maximum a posteriori (MAP) clock model; however, this Bayes factor estimate may suffer when the posterior probability of the MAP model approaches 1. Here, we compare these two recent developments with the HME, stabilized/smoothed HME (sHME), and AICM, using both synthetic and empirical data. Our comparison shows reassuringly that MAP identification and its Bayes factor provide similar performance to PS and SS and that these approaches considerably outperform HME, sHME, and AICM in selecting the correct underlying clock model. We also illustrate the importance of using proper priors on a large set of empirical data sets.
Keywords: model comparison, marginal likelihood, Bayes factors, path sampling, stepping-stone sampling, model averaging, molecular clock, Bayesian inference, phylogeny, BEAST
Recent developments in marginal likelihood estimation in Bayesian phylogenetics and molecular evolution have generated effective procedures to compare a wide range of evolutionary hypotheses and select the most likely model given the data at hand. These developments include path sampling (PS, Ogata 1989; Gelman and Meng 1998; Lartillot and Philippe 2006) and stepping-stone sampling (SS, Xie et al. 2011), which require additional programming and come at an increased computational cost compared with posterior-sampling methods such as the harmonic mean estimator (HME, Newton and Raftery 1994), the stabilized/smoothed harmonic mean estimator (sHME, Redelings and Suchard 2005), and a posterior simulation-based analog of Akaike’s information criterion through Markov chain Monte Carlo (AICM, Raftery et al. 2007). Newton and Raftery (1994) pointed out that, although the HME is consistent and asymptotically unbiased, it has infinite variance and so may not perform well in practice. The posterior-sampling methods have in fact been shown to systematically overestimate the marginal likelihood, whereas PS and SS accurately estimate the marginal likelihood with much lower error (Xie et al. 2011), compensating for their increased cost.
Recently, Baele et al. (2012) analyzed both synthetic and empirical data to compare the performance of PS, SS, HME, and AICM in selecting molecular clock models and models of demographic change. In that study, the HME fails to yield reliable selection of the true model, and the AICM performs moderately better and may provide a useful initial evaluation of model choice. The authors further demonstrate that PS and SS substantially outperform both the HME and AICM when the true model is known and that conclusions made concerning previous analyses for three real-world data sets require adjustment given the outcome of PS and SS compared with the HME.
Although quantifying the marginal likelihood of alternative models is invaluable when it relates to hypothesis testing, model selection and its search for a single best-fit model typically ignores uncertainty about the “correct” model specification and can lead to overconfident inferences (Hoeting et al. 1999). Bayesian model averaging (BMA) approaches have been proposed to explicitly address model uncertainty by forming a posterior distribution over a set of candidate models (Madigan and Raftery 1994). In general, BMA does not provide a method for identifying the most likely model within the candidate set of models, as the aim of BMA is often orthogonal to model selection efforts. However, specific BMA constructions can yield estimates of the posterior probabilities of each of the candidate models (Carlin and Chib 1995). As dividing the posterior odds of two models by their prior odds returns their Bayes factor, or ratio of marginal likelihoods, these constructions do offer a way to quantify posterior probability support for the different models within the candidate set of models. A potential limitation to this approach centers on the accuracy to which one can estimate each model’s posterior probability, because these estimates often fall very close 0 or 1 without adjusting the prior probabilities (Suchard et al. 2005).
In recent work, Li and Drummond (2012) developed a BMA approach in which the candidate set includes a small number of relaxed molecular clock models in Bayesian phylogenetics. Such relaxed clock models present a useful method for removing the assumption of a strict molecular clock and assume no a priori correlation of the rates on adjacent branches of the tree. Instead, the rate on each branch of the tree is drawn independently and identically from an underlying rate distribution. Two main candidates for the rate distribution among branches are often employed: an uncorrelated exponential distribution, denoted UCED, and an uncorrelated lognormal distribution, denoted UCLD. Li and Drummond (2012) show that their BMA method accurately recovers the true underlying distribution of rates. Because their construction returns estimates of the posterior probability of each model, Li and Drummond (2012) also examine the performance of identifying the maximum a posteriori (MAP) model under BMA as a model selection criterion. The authors found that across a large set of alignments taken from a data set of 12 mammalian species, a model with log-normally distributed rates is more likely than exponentially distributed rates in most of the alignments; this is an expected result given that the exponential distribution has a mode at 0, whereas the log-normal distribution allows for a more flexible modeling of the rates and provides confirmation of successful model selection. As far as we know, estimated Bayes factors in favor of the MAP model under BMA have not yet been compared with Bayes factors obtained from state-of-the-art marginal likelihood estimation procedures, such as PS and SS, in phylogenetics, which is the aim of this study.
Here, we reanalyze the synthetic and empirical data sets previously analyzed by Li and Drummond (2012) using the HME, sHME, AICM, PS, SS, and MAP (see Materials and Methods for more information concerning the simulation process and prior specifications). Additionally, we have included further simulations under a collection of trees arising from a Yule birth process rather than the less realistic balanced tree in Li and Drummond (2012). A total of 100 simulations were run under both the uncorrelated relaxed molecular clock assuming a UCED and a UCLD. The results of the simulations are summarized in table 1.
Table 1.
Model Selection Performance for 100 Simulated Data Sets under either a Balanced or Yule Tree and Two Relaxed Molecular Clock Models Using HME, sHME, AICM, PS, SS, and the MAP Estimated under BMA.
| Tree | Clock | HME | sHME | AICM | PS | SS | MAP |
|---|---|---|---|---|---|---|---|
| Balanced | UCED | 92 | 100 | 100 | 94 | 94 | 90 |
| Balanced | UCLD | 28 | 5 | 1 | 99 | 99 | 99 |
| Yule | UCED | 92 | 100 | 100 | 99 | 99 | 97 |
| Yule | UCLD | 11 | 1 | 1 | 61 | 61 | 65 |
For the data simulated under the UCED clock model for both the balanced tree and the trees generated under a Yule birth process, the HME, PS, SS, and MAP recover the true model in high frequencies (between 90% and 94%) and the sHME and AICM always recover the true model. Given that the HME has an infinite variance, its performance (and certainly that of the sHME and AICM) is unexpectedly good. However, when the data are simulated under the UCLD clock model assuming a balanced tree, the HME, sHME, and AICM recover the true model only in very low frequencies (and in even lower frequencies for the Yule trees), whereas PS, SS, and MAP almost always classify the relaxed clock model correctly for the simulations under a balanced tree. The results for MAP are consistent with those reported by Li and Drummond (2012) (where 83 and 100 correct classifications were obtained using the MAP under the UCED and UCLD clock model, respectively). The increase in number of correct classifications we observe may be attributed to the use of proper priors in the analyses performed in this study. PS, SS, and MAP still clearly outperform HME, sHME, and AICM when simulating under a Yule birth process but no longer achieve the near-ideal performance of the simulations performed under a balanced tree. In conclusion, table 1 shows that PS, SS, and MAP offer similar performance in assessing the correct relaxed molecular clock model and clearly outperform the HME, sHME, and AICM.
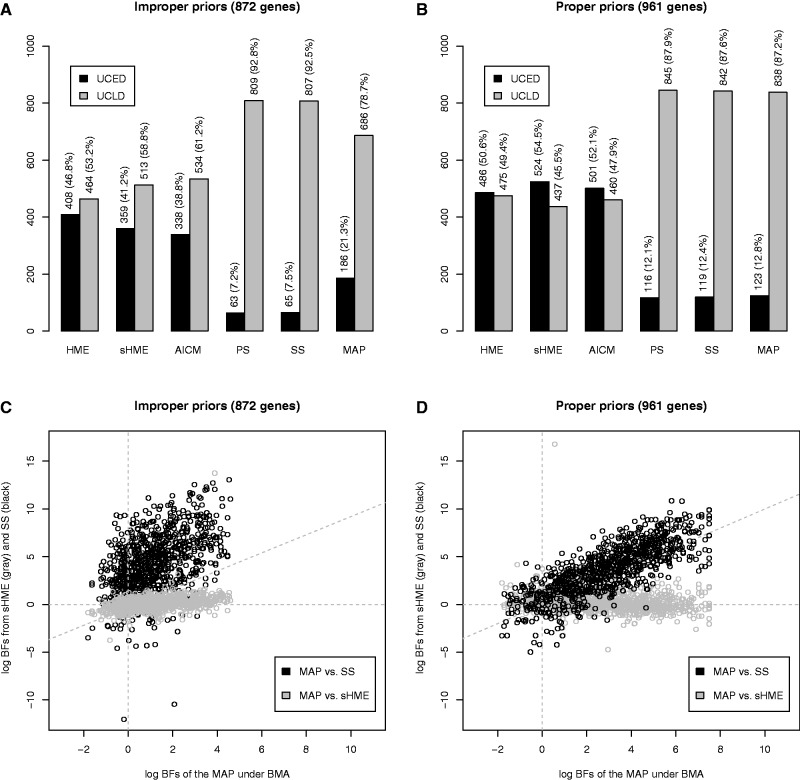
We also applied these methods to the large set of alignments taken from 12 mammalian species analyzed in the work of Li and Drummond (2012), which originally contained 1,056 alignments. After removing 54 alignments for which convergence could not be reached (even after 200 million iterations) under BMA and 41 alignments for which the HME provides inaccurate estimates (for either the UCED or UCLD model or both; see Li and Drummond [2012] for more detail) that do not reflect the actual Bayes factor, 961 genes were retained, which serve as the starting point for the analyses in this article. While convergence issues appear when using BMA and the HME, PS and SS on the other hand naturally have difficulties simulating from the prior, due to the improper priors provided in the original analyses, resulting in failure to calculate a Bayes factor for 89 additional alignments. Comparing the analyses for which no convergence problems (for HME, sHME, and AICM) and no prior sampling problems (for PS and SS) were reported hence yielded 872 genes for which the model selection process using HME, sHME, AICM, PS, SS, and MAP could be performed (fig. 1).
Fig. 1.
Results for the analysis of a large set of mammalian genes: (A) model selection results for the analysis of 872 genes using improper priors using the different estimators; (B) model selection results for the analysis of 961 genes using proper priors; (C) comparison of the log Bayes factor estimates for a common set of 872 genes for the MAP and sHME (gray) and for the MAP and SS (black), assuming improper priors; and (D) comparison of the log Bayes factor estimates for a common set of 961 genes for the MAP and sHME (gray) and for the MAP and SS (black), assuming proper priors.
We first focus on reanalyzing these genes using the (improper) prior assumptions of the original publication (Li and Drummond 2012). At this point, it is crucial to stress that an improper prior distribution frequently leads to an infinite marginal likelihood (even if the estimation method returns a noninfinite value), which in turn implies that the Bayes factor is not well defined (Spiegelhalter and Smith 1982; Friel and Petitt 2008), making inference based on improper priors highly suspect. Despite this importance, attributing little attention to proper prior specification has become common practice when calculating Bayes factors in phylogenetics, and this can inadvertently affect model comparison conclusions as we demonstrate here.
When using improper priors, the HME selects the UCED model over the UCLD model in 47% of the genes (and the sHME in 41% of the genes), whereas the AICM prefers the UCED model in 39% of the genes (fig. 1A). On the other hand, PS and SS select the UCED model over the UCLD model in only approximately 7% of the genes. MAP yields a result in between the posterior-sampling methods and PS/SS, selecting the UCED model in for 21% of the genes. Even though PS, SS, and MAP have both been shown to be more accurate than the HME (Baele et al. 2012; Li and Drummond 2012), their performance differs considerably, with MAP selecting the UCED model nearly three times as much as PS and SS.
Using proper priors (see Materials and Methods), however, the results change substantially, as can be seen in figure 1B. Contrary to when assuming improper priors, PS and SS no longer suffer from prior sampling issues and yield an estimate of the marginal likelihood for all 961 genes. In this case, the HME selects the UCED model in 51% of the genes (and the sHME in 55% of the genes), whereas the AICM prefers the UCED clock model over the UCLD clock model in 52% of the genes. PS and SS select the UCED model over the UCLD model in only 12% of the genes, and MAP prefers the UCED model in 13% of the genes. The use of proper priors therefore appears to result in a convergence of the model preference for PS, SS, and MAP. To confirm this, we checked to which degree the classification results overlap between SS, sHME, and MAP. In the case of improper priors, MAP and SS yield the same model classification in 78% of the genes, whereas MAP and sHME do so for 70% of the genes and SS and sHME only agree in 60% of the genes. In the case of proper priors, however, MAP and SS yield the same model classification in 90% of the genes, whereas MAP and sHME agree in merely 52% of the genes, and SS and sHME agree in 51% of the genes. This indicates that in terms of model classification for PS, SS, and MAP, the results are highly correlated and clearly different from those of HME, sHME, and AICM, which select the UCED model in over half the genes.
In figure 1C, we show the original scatter plot employing improper priors of the log Bayes factors for the mammalian data calculated using MAP versus the HME (in gray) and a scatter plot of the log Bayes factors calculated by using MAP versus SS (in black). The correlation coefficients between the different log Bayes factor estimators appear to be rather low, that is, 0.37 between MAP and HME and 0.44 between MAP and SS. In figure 1D, we summarize the same comparison for the mammalian data between the log Bayes factors when specifying proper priors, with the log Bayes factor comparison between MAP and sHME again shown in gray and the log Bayes factor comparison between MAP and SS shown in black. Outliers for both figure 1C and D were removed by computing leverage coefficients (Hoaglin and Welsch 1978) as in Li and Drummond (2012). When using proper priors, the correlation coefficient between MAP and HME equals −0.18, whereas the correlation coefficient between MAP and SS was 0.79, indicating a strong agreement for their model classification. Hence, the agreement between MAP and SS strongly depends on the specification of proper priors, leading to estimable marginal likelihoods. Similar conclusions can be reached for MAP and PS (data not shown).
In conclusion, our simulations demonstrate that PS, SS, and MAP outperform HME, sHME, and AICM when comparing relaxed molecular clock models, achieving correct classification in more than 90% of the simulated data sets generated on a balanced tree. The analysis of real gene data sets also shows that PS, SS, and MAP offer very similar results. These models select the UCLD model in 87% of the genes, whereas HME, sHME, and AICM select the UCLD model in less than 50% of the genes and are hence strongly drawn toward the UCED model. Further, we have shown the importance of using proper priors when performing model selection. Only when assuming proper priors does the calculation of (log) Bayes factors make sense and offer a valid approach for performing model selection. Once proper priors are used, the log Bayes factors of the MAP under BMA and PS/SS are highly correlated and hence their model selection outcomes very similar. This is not the case for MAP and sHME, of which the (log) Bayes factors are uncorrelated, showing once again the poor performance of the sHME when classifying models. MAP seems to be the preferred model selection approach for the problems presented in this article as it removes the burden of model selection from the user and requires the least amount of computation. However, it is not generally applicable between any two or more models that need to be compared and requires a specific strategy for each class of models. Although computationally more demanding, PS and SS allow for a more general comparison of models and can address cases for which a candidate set under BMA is unavailable.
Materials and Methods
We calculate marginal likelihoods using PS (Gelman and Meng 1998; Ogata 1989; Lartillot and Philippe 2006), SS (Xie et al. 2011), HME (Newton and Raftery 1994), and sHME (Redelings and Suchard 2005). We use the recommendation of Xie et al. (2011) in selecting β values between the path from prior to posterior according to evenly spaced quantiles of a Beta(α,1.0) distribution and therefore choose α = 0.3, which places most of the computational effort on β values near zero, which should result in increased accuracy. Additionally, we employ the AICM to perform model selection (Raftery et al. 2007). We note that a posterior simulation-based analog of the Bayesian information criterion through Markov chain Monte Carlo has also been proposed (Raftery et al. 2007), an approach that has a more direct Bayesian justification but requires specification of a sample size for each parameter, which may be problematical in some applications. For more detailed information on these methods and the way they are implemented in BEAST (Drummond et al. 2012), we refer interested readers to Baele et al. (2012). BMA between the UCED and UCLD clock models was performed using the approach of Li and Drummond (2012) that assumes that the prior probability of each model is equal, that is, there is no prior knowledge as to which model is preferred. As a consequence, the ratio of the posterior probabilities of the two models equals the Bayes factor as the prior odds equals 1.
Data were first simulated using a balanced tree of 32 taxa and an additional outgroup, with the divergence times on each branch set to 5 time units, except the outgroup branch which had a length of 30 to make the tree ultrametric. A second set of simulations was generated using a collection of 100 trees generated using a Yule birth process with a birth rate of 0.2, leading to an average branch length of ∼2.5 time units. For each of the branches on a tree, we assigned a rate of substitution drawn from either a UCED with a mean of 0.005 or a UCLD with a mean of 0.005 and variance of 0.004. One hundred realizations of rates were simulated under each of the two relaxed clock models, and alignments of 1,000 bp in length were subsequently generated using Seq-Gen (Rambaut and Grassly 1997) under a Hasegawa–Kishino–Yano (HKY, Hasegawa et al. 1985) model with gamma-distributed rate heterogeneity across sites (Yang 1996) with a transition–transversion ratio of 3.0 and a shape parameter of 0.5. We used the simulation settings described in Li and Drummond (2012) but fitted the analyses with proper priors. A proper prior is a probability distribution that integrates to 1. The frequently used constant function on an infinite interval is often inaccurately called a uniform distribution, although it is actually an example of an improper prior. In general, the use of such priors can lead to posterior distributions that do not exist (i.e., are not probability distributions). In practice, because standard floating-point representations of numbers have a maximum attainable value, the implementation of this prior in a computer can actually be regarded as proper, but regardless, such priors are effectively improper and provide a great challenge to MCMC sampling. This is evident in the results presented here. Specifically, we used the following priors: a Yule pure birth process was used as a prior on the speciation process for the simulations (Yule 1924), with a diffuse normally distributed prior on the log birth rate (log μ = 1.0, log σ = 1.25); a birth–death process (Gernhard 2008) was used as a prior on the speciation process for the empirical data analyses with a diffuse lognormal prior (μ = 17.5, log σ = 2.5), centered on the mean of the estimated birth rates found in Li and Drummond (2012), for the log growth rate of the birth–death process and a uniform prior (between 0.0 and 1.0) on the relative death rate; a diffuse normally distributed prior on the log transition–transversion parameter of the HKY model (log μ = 1.0, log σ = 1.25) for the simulations; diffuse gamma distributed priors on the relative rate parameters of the general time-reversible (GTR) model (Tavaré 1986) for the empirical data analyses (Gamma(0.05;20.0) for _r_AG; Gamma(0.05;10.0) for _r_AC, _r_AT, _r_CG, and _r_GT); an exponential prior (with mean 0.5) on the rate heterogeneity parameter (Yang 1996); an exponential prior (with mean 1/3) on the standard deviation of the UCLD clock model; and a Dirichlet(1,1,1,1) distribution on the base frequencies. For one of the empirical data sets analyzed in this article, we provide five example XML files in the supplementary material, Supplementary Material online: one illustrating the use of the BMA approach, two illustrating the use of the posterior-based estimators (HME, sHME, and AICM; one for the UCED and one for the UCLD model), and two illustrating the use of the PS and SS approaches (one for the UCED and one for the UCLD model).
Supplementary Material
Supplementary material is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Supplementary Data
Acknowledgments
The authors thank the associate editor, Paul Lewis, and one anonymous referee for helpful comments on preparing this paper. This work was supported by the European Union Seventh Framework Programme [FP7/2007–2013] under Grant Agreement no. 278433-PREDEMICS and ERC Grant agreement no. 260864, by National Evolutionary Synthesis Center (NESCent) through a working group (Software for Bayesian Evolutionary Analysis), and partially by NIH grants R01 GM086887 and HG006139 and NSF grant DMS0856099 to M.A.S. The computational resources (Stevin Supercomputer Infrastructure) and services used in this work were provided by Ghent University, the Hercules Foundation, and the Flemish Government Department EWI. Further research was partially completed while A.J.D., M.A.S., and P.L. were visiting the Institute for Mathematical Sciences, National University of Singapore, in 2011.
References
- Baele G, Lemey P, Bedford T, Rambaut A, Suchard MA, Alekseyenko AV. Improving the accuracy of demographic and molecular clock model comparison while accommodating phylogenetic uncertainty. Mol Biol Evol. 2012;29:2157–2167. doi: 10.1093/molbev/mss084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlin BP, Chib S. Bayesian model choice via Markov chain Monte Carlo. J R Stat Soc B. 1995;57:473–484. [Google Scholar]
- Drummond AJ, Suchard MA, Xie D, Rambaut A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol Biol Evol. 2012;29:1969–1973. doi: 10.1093/molbev/mss075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friel N, Petitt AN. Marginal likelihood estimation via power posteriors. J R Stat Soc B. 2008;70:589–607. [Google Scholar]
- Gelman A, Meng XL. Simulating normalizing constants: from importance sampling to bridge sampling to path sampling. Stat Sci. 1998;13:163–185. [Google Scholar]
- Gernhard T. The conditioned reconstructed process. J Theor Biol. 2008;253:769–778. doi: 10.1016/j.jtbi.2008.04.005. [DOI] [PubMed] [Google Scholar]
- Hasegawa M, Kishino H, Yano T. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J Mol Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- Hoaglin DC, Welsch RE. The hat matrix in regression and ANOVA. Am Stat. 1978;32:17–22. [Google Scholar]
- Hoeting JA, Madigan D, Raftery AE, Volinsky CT. Bayesian model averaging: a tutorial. Stat Sci. 1999;14:382–417. [Google Scholar]
- Lartillot N, Philippe H. Computing Bayes factors using thermodynamic integration. Syst Biol. 2006;55:195–207. doi: 10.1080/10635150500433722. [DOI] [PubMed] [Google Scholar]
- Li WLS, Drummond AJ. Model averaging and Bayes factor calculation of relaxed molecular clocks in Bayesian phylogenetics. Mol Biol Evol. 2012;29:751–761. doi: 10.1093/molbev/msr232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madigan D, Raftery AE. Model selection and accounting for model uncertainty in graphical models using Occam’s window. J Am Stat Assoc. 1994;89:1535–1546. [Google Scholar]
- Newton MA, Raftery AE. Approximating Bayesian inference with the weighted likelihood bootstrap. J R Stat Soc B. 1994;56:3–48. [Google Scholar]
- Ogata Y. A Monte Carlo method for high dimensional integration. Num Math. 1989;55:137–157. [Google Scholar]
- Raftery A, Newton M, Satagopan J, Krivitsky P. Estimating the integrated likelihood via posterior simulation using the harmonic mean identity. In: Bernardo JM, Bayarri MJ, Berger JO, editors. Bayesian statistics. New York: Oxford University Press; 2007. pp. 1–45. [Google Scholar]
- Rambaut A, Grassly NC. Seq-gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput Appl Biosci. 1997;13:235–238. doi: 10.1093/bioinformatics/13.3.235. [DOI] [PubMed] [Google Scholar]
- Redelings BD, Suchard MA. Joint Bayesian estimation of alignment and phylogeny. Syst Biol. 2005;54:401–418. doi: 10.1080/10635150590947041. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Smith AFM. Bayes factors for linear and log-linear models with vague prior information. J R Stat Soc B (Methodological). 1982;44:377–387. [Google Scholar]
- Suchard M, Weiss R, Sinsheimer J. Models for estimating Bayes factors with applications to phylogeny and tests of monophyly. Biometrics. 2005;61:665–673. doi: 10.1111/j.1541-0420.2005.00352.x. [DOI] [PubMed] [Google Scholar]
- Tavaré S. Some probabilistic and statistical problems in the analysis of DNA sequences. In: Waterman MS, editor. Some mathematical questions in biology: DNA sequence analysis. Providence (RI): American Mathematical Society; 1986. pp. 57–86. [Google Scholar]
- Xie W, Lewis PO, Fan Y, Kuo L, Chen MH. Improving marginal likelihood estimation for Bayesian phylogenetic model selection. Syst Biol. 2011;60:150–160. doi: 10.1093/sysbio/syq085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. Among-site rate variation and its impact on phylogenetic analyses. Trends Ecol Evol. 1996;11:367–372. doi: 10.1016/0169-5347(96)10041-0. [DOI] [PubMed] [Google Scholar]
- Yule GU. A mathematical theory of evolution based on the conclusions of Dr. J.C. Willis. F.R.S. Philos Trans R. Soc Lond B Biol Sci. 1924;213:21–87. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Data