Rethinking the evolutionary theory of aging: transfers, not births, shape senescence in social species - PubMed (original) (raw)
Rethinking the evolutionary theory of aging: transfers, not births, shape senescence in social species
Ronald D Lee. Proc Natl Acad Sci U S A. 2003.
Abstract
The classic evolutionary theory of aging explains why mortality rises with age: as individuals grow older, less lifetime fertility remains, so continued survival contributes less to reproductive fitness. However, successful reproduction often involves intergenerational transfers as well as fertility. In the formal theory offered here, age-specific selective pressure on mortality depends on a weighted average of remaining fertility (the classic effect) and remaining intergenerational transfers to be made to others. For species at the optimal quantity-investment tradeoff for offspring, only the transfer effect shapes mortality, explaining postreproductive survival and why juvenile mortality declines with age. It also explains the evolution of lower fertility, longer life, and increased investments in offspring.
Figures
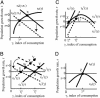
Fig. 1.
(A) Equilibrium population size and age distribution, reflecting density and intergenerational transfers (see Population Equilibrium with Intergenerational Transfers for details). (B) The effect on_r_ and γ of a mortality-reducing mutation when the balance curve is downward sloping (see Mutation and Selection Without Age). (C) Selection effects on the left of a hump, where the classical effects are reversed. Evolution moves toward the optimal equilibrium at the peak (see The Evolutionary Trajectory to the Optimal Equilibrium). (D) The optimal equilibrium is evolutionarily stable (see The Evolutionary Trajectory to the Optimal Equilibrium).
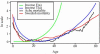
Fig. 2.
The force of selection on mortality is a weighted average of the fertility effect and the transfer effect (Eq. 6 in Appendix), illustrated for Ache forager–horticulturist data (–37). Short dashes, selection to right of hump; long dashes, selection to left of hump; solid line, selection at peak of hump.
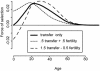
Fig. 3.
Comparison of actual mortality schedules with predicted mortality for classical theory and present theory. Mortality should be inversely proportional to force of selection, so logarithms of age-specific death rates, 1/F(a), and 1/T(a) are shown. Fertility, mortality, and transfers are for Ache (–37). Also plotted is mortality for 18th-century Sweden (data from Human Mortality Database, University of California, Berkeley, and Max Planck Institute for Demographic Research, Rostock, Germany, and available at
or
). All curves are adjusted to have the same minimum at 0, because only shape is being compared. Actual juvenile and adult mortalities agree well with the transfer theory and poorly with classical theory.
Comment in
- Economics and the evolution of life histories.
Rogers AR. Rogers AR. Proc Natl Acad Sci U S A. 2003 Aug 5;100(16):9114-5. doi: 10.1073/pnas.1733942100. Epub 2003 Jul 28. Proc Natl Acad Sci U S A. 2003. PMID: 12886004 Free PMC article. No abstract available.
Similar articles
- Explaining the optimality of U-shaped age-specific mortality.
Chu CY, Chien HK, Lee RD. Chu CY, et al. Theor Popul Biol. 2008 Mar;73(2):171-80. doi: 10.1016/j.tpb.2007.11.005. Epub 2007 Nov 28. Theor Popul Biol. 2008. PMID: 18178233 Free PMC article. - Intergenerational transfers in industrialised countries: effects of age distribution and economic institutions.
Ermisch J. Ermisch J. J Popul Econ. 1989;1(4):269-84. doi: 10.1007/BF00166068. J Popul Econ. 1989. PMID: 12282852 - The importance of elders: Extending Hamilton's force of selection to include intergenerational transfers.
Davison R, Gurven M. Davison R, et al. Proc Natl Acad Sci U S A. 2022 Jul 12;119(28):e2200073119. doi: 10.1073/pnas.2200073119. Epub 2022 Jul 6. Proc Natl Acad Sci U S A. 2022. PMID: 35867741 Free PMC article. - What Is Antagonistic Pleiotropy?
Mitteldorf J. Mitteldorf J. Biochemistry (Mosc). 2019 Dec;84(12):1458-1468. doi: 10.1134/S0006297919120058. Biochemistry (Mosc). 2019. PMID: 31870250 Review. - The origins of human ageing.
Kirkwood TB. Kirkwood TB. Philos Trans R Soc Lond B Biol Sci. 1997 Dec 29;352(1363):1765-72. doi: 10.1098/rstb.1997.0160. Philos Trans R Soc Lond B Biol Sci. 1997. PMID: 9460059 Free PMC article. Review.
Cited by
- On the evolution of intergenerational division of labor, menopause and transfers among adults and offspring.
Cyrus CC, Lee RD. Cyrus CC, et al. J Theor Biol. 2013 Sep 7;332:171-80. doi: 10.1016/j.jtbi.2013.04.031. Epub 2013 May 3. J Theor Biol. 2013. PMID: 23648187 Free PMC article. - The molecular basis of socially induced egg-size plasticity in honey bees.
Han B, Wei Q, Amiri E, Hu H, Meng L, Strand MK, Tarpy DR, Xu S, Li J, Rueppell O. Han B, et al. Elife. 2022 Nov 8;11:e80499. doi: 10.7554/eLife.80499. Elife. 2022. PMID: 36346221 Free PMC article. - Sexual dimorphism and sexual selection: a unified economic analysis.
Cyrus Chu CY, Lee RD. Cyrus Chu CY, et al. Theor Popul Biol. 2012 Dec;82(4):355-63. doi: 10.1016/j.tpb.2012.06.002. Epub 2012 Jun 11. Theor Popul Biol. 2012. PMID: 22699007 Free PMC article. - Early mortality saves energy: estimating the energetic cost of excess offspring in a seabird.
Vedder O, Zhang H, Bouwhuis S. Vedder O, et al. Proc Biol Sci. 2017 Feb 22;284(1849):20162724. doi: 10.1098/rspb.2016.2724. Proc Biol Sci. 2017. PMID: 28202814 Free PMC article. - Damage segregation at fissioning may increase growth rates: a superprocess model.
Evans SN, Steinsaltz D. Evans SN, et al. Theor Popul Biol. 2007 Jun;71(4):473-90. doi: 10.1016/j.tpb.2007.02.004. Epub 2007 Mar 12. Theor Popul Biol. 2007. PMID: 17442356 Free PMC article.
References
- Medawar, P. B. (1952) An Unsolved Problem in Biology (Lewis, London).
- Williams, G. C. (1957) Evolution (Lawrence, Kans.) 11, 398-411.
- Hamilton, W. E. (1966) J. Theor. Biol. 12, 12-45. - PubMed
- Rose, M. R. (1991) Evolutionary Biology of Aging (Oxford Univ. Press, New York).
MeSH terms
LinkOut - more resources
Full Text Sources
Medical