Parameter estimation in biochemical pathways: a comparison of global optimization methods - PubMed (original) (raw)

Comparative Study

. 2003 Nov;13(11):2467-74.

doi: 10.1101/gr.1262503. Epub 2003 Oct 14.

Affiliations

Comparative Study

Parameter estimation in biochemical pathways: a comparison of global optimization methods

Carmen G Moles et al. Genome Res. 2003 Nov.

Abstract

Here we address the problem of parameter estimation (inverse problem) of nonlinear dynamic biochemical pathways. This problem is stated as a nonlinear programming (NLP) problem subject to nonlinear differential-algebraic constraints. These problems are known to be frequently ill-conditioned and multimodal. Thus, traditional (gradient-based) local optimization methods fail to arrive at satisfactory solutions. To surmount this limitation, the use of several state-of-the-art deterministic and stochastic global optimization methods is explored. A case study considering the estimation of 36 parameters of a nonlinear biochemical dynamic model is taken as a benchmark. Only a certain type of stochastic algorithm, evolution strategies (ES), is able to solve this problem successfully. Although these stochastic methods cannot guarantee global optimality with certainty, their robustness, plus the fact that in inverse problems they have a known lower bound for the cost function, make them the best available candidates.

PubMed Disclaimer

Figures

Figure 1

Figure 1

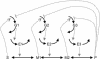
The model metabolic pathway used in these studies. Solid arrows represent mass flow, dashed arrows represent kinetic regulation; arrow ends represent activation, blunt ends inhibition. S and P are the pathway substrate and product and are held at constant concentrations; M1 and M2 are intermediate metabolites of the pathway; E1, E2, and E3 are the enzymes; G1, G2, and G3 are the mRNA species for the enzymes.

Figure 2

Figure 2

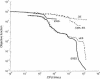
Convergence curves (objective function versus computation time, in seconds, using a PC/Pentium III 866 MHz).

Figure 3

Figure 3

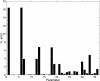
Histogram of the results obtained with the multistart local method.

Figure 4

Figure 4

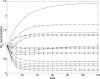
_M_2 predicted (continuous line) and experimental (marker) behavior for the 16 experiments.

Figure 5

Figure 5

_E_1 predicted (continuous line) and experimental (marker) behavior for the 16 experiments.

Figure 6

Figure 6

Relative error (%) for the estimated parameters (for the best solution, obtained by SRES).

Similar articles

Cited by

References

    1. Ali, M.M., Storey, C., and Törn, A. 1997. Application of stochastic global optimization algorithms to practical problems. J. Optim. Theory Appl. 95: 545-563.
    1. Anonymous. 2000. Optimization toolbox user's guide. The Math Works Inc., Natick, MA.
    1. Bäck, T. 1996. Evolution strategies: An alternative evolutionary algorithm. In Artificial evolution (eds. J.M. Alliott et al.), pp. 3-20. Springer, Berlin.
    1. Balsa-Canto, E., Alonso, A.A., and Banga, J.R. 1998. Dynamic optimization of bioprocesses: Deterministic and stochastic strategies. In Proceedings of ACoFop IV (Automatic Control of Food and Biological Processes), (eds. C. Skjoldebremd and G. Trystrom), pp. 2-23. Göteborg, Sweden.
    1. Banga, J.R. and Casares, J.J. 1987. ICRS: Application to a wastewater treatment plant model. In IChemE Symposium Series No. 100, pp. 183-192. Pergamon Press, Oxford, UK.

WEB SITE REFERENCES

    1. http://www.beowulf.org; technology for cluster computing.
    1. http://www.gepasi.org; Gepasi biochemical simulation package.
    1. http://www.globus.org; technology for grid computing.
    1. http://www.mathworks.com; Matlab.

Publication types

MeSH terms

Substances

LinkOut - more resources