Kinetics of influenza A virus infection in humans - PubMed (original) (raw)
Kinetics of influenza A virus infection in humans
Prasith Baccam et al. J Virol. 2006 Aug.
Abstract
Currently, little is known about the viral kinetics of influenza A during infection within an individual. We utilize a series of mathematical models of increasing complexity, which incorporate target cell limitation and the innate interferon response, to examine influenza A virus kinetics in the upper respiratory tracts of experimentally infected adults. The models were fit to data from an experimental H1N1 influenza A/Hong Kong/123/77 infection and suggest that it is important to include the eclipse phase of the viral life cycle in viral dynamic models. Doing so, we estimate that after a delay of approximately 6 h, infected cells begin producing influenza virus and continue to do so for approximately 5 h. The average lifetime of infected cells is approximately 11 h, and the half-life of free infectious virus is approximately 3 h. We calculated the basic reproductive number, R(0), which indicated that a single infected cell could produce approximately 22 new productive infections. This suggests that antiviral treatments have a large hurdle to overcome in moderating symptoms and limiting infectiousness and that treatment has to be initiated as early as possible. For about 50% of patients, the curve of viral titer versus time has two peaks. This bimodal behavior can be explained by incorporating the antiviral effects of interferon into the model. Our model also compared well to an additional data set on viral titer after experimental infection and treatment with the neuraminidase inhibitor zanamivir, which suggests that such models may prove useful in estimating the efficacies of different antiviral therapies for influenza A infection.
Figures
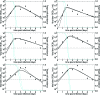
FIG. 1.
Fits of the target cell-limited model without delay (equations 1 to 3) (solid lines) and with delay (equations 5 to 8) (dashed lines) to experimental data (filled squares) from H1N1 experimental influenza virus infections (28). The graphs present viral titers in TCID50/ml of nasal wash (black) and fractions of target cells remaining (blue) over the courses of the infections. The horizontal dotted lines mark the limit of detection for viral titer.
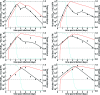
FIG. 2.
Fits of the target cell-limited model with delay that incorporates interferon (equations 5 to 8 and 9 to 11) to experimental data (filled squares) from H1N1 experimental influenza virus infections (28). The graphs present the viral titers (black), the IFN concentrations (red), and the fractions of target cells remaining (blue) over the courses of the infections. The horizontal dotted lines mark the limit of detection for viral titer.
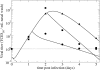
FIG. 3.
Course of influenza virus infections with and without the neuraminidase inhibitor zanamivir given intranasally. The average virus titers for 26 volunteers given placebo (solid triangles), 31 volunteers given an NI early (26 or 32 h) (filled circles), and 12 volunteers given an NI delayed (50 h) (filled squares) following experimental infection are shown. The predicted virus titers using the target cell-limited model with delay (solid line) are shown for the placebo group, the early-treatment group, and the delayed-treatment group. The horizontal dotted line marks the limit of detection for viral titer. The parameter values used to describe the infections before therapy (placebo group) are V_0 = 0.25 TCID50/ml, β = 1.4 × 10−2 (TCID50/ml)−1 · d−1, k = 3.2 d−1, p = 2.7 × 10−5TCID50/ml · d−1, c = 3.2 d−1, and δ = 3.2 d−1. Those parameter values are held constant for the treatment groups, except for p, which was set to 0.03_p from time of drug administration onwards, namely, from 1.2 d and 2.08 d for the early- and delayed-treatment groups, respectively. Prophylactic use of an NI was modeled as a reduction in viral production rate by 97% at time of infection (dashed line). Experimental data were taken from Hayden et al. (15).
Similar articles
- Efficacy and safety of the neuraminidase inhibitor zanamivir in the treatment of influenzavirus infections. GG167 Influenza Study Group.
Hayden FG, Osterhaus AD, Treanor JJ, Fleming DM, Aoki FY, Nicholson KG, Bohnen AM, Hirst HM, Keene O, Wightman K. Hayden FG, et al. N Engl J Med. 1997 Sep 25;337(13):874-80. doi: 10.1056/NEJM199709253371302. N Engl J Med. 1997. PMID: 9302301 Clinical Trial. - Oseltamivir resistance in influenza A (H5N1) infection.
Gupta RK, Nguyen-Van-Tam JS. Gupta RK, et al. N Engl J Med. 2006 Mar 30;354(13):1423-4; author reply 1423-4. doi: 10.1056/NEJMc060077. N Engl J Med. 2006. PMID: 16571890 No abstract available. - Antiviral drugs in influenza: an adjunct to vaccination in some situations.
[No authors listed] [No authors listed] Prescrire Int. 2006 Feb;15(81):21-30. Prescrire Int. 2006. PMID: 16548114 - Influenza virus neuraminidase inhibitors.
Gubareva LV, Kaiser L, Hayden FG. Gubareva LV, et al. Lancet. 2000 Mar 4;355(9206):827-35. doi: 10.1016/S0140-6736(99)11433-8. Lancet. 2000. PMID: 10711940 Review. - Zanamivir: from drug design to the clinic.
Elliott M. Elliott M. Philos Trans R Soc Lond B Biol Sci. 2001 Dec 29;356(1416):1885-93. doi: 10.1098/rstb.2001.1021. Philos Trans R Soc Lond B Biol Sci. 2001. PMID: 11779388 Free PMC article. Review.
Cited by
- Influenza virus shedding and symptoms: Dynamics and implications from a multiseason household transmission study.
Morris SE, Nguyen HQ, Grijalva CG, Hanson KE, Zhu Y, Biddle JE, Meece JK, Halasa NB, Chappell JD, Mellis AM, Reed C, Biggerstaff M, Belongia EA, Talbot HK, Rolfes MA. Morris SE, et al. PNAS Nexus. 2024 Aug 21;3(9):pgae338. doi: 10.1093/pnasnexus/pgae338. eCollection 2024 Sep. PNAS Nexus. 2024. PMID: 39246667 Free PMC article. - An agent-based nested model integrating within-host and between-host mechanisms to predict an epidemic.
Tatsukawa Y, Arefin MR, Kuga K, Tanimoto J. Tatsukawa Y, et al. PLoS One. 2023 Dec 15;18(12):e0295954. doi: 10.1371/journal.pone.0295954. eCollection 2023. PLoS One. 2023. PMID: 38100436 Free PMC article. - In-host Mathematical Modelling of COVID-19 in Humans.
Hernandez-Vargas EA, Velasco-Hernandez JX. Hernandez-Vargas EA, et al. Annu Rev Control. 2020;50:448-456. doi: 10.1016/j.arcontrol.2020.09.006. Epub 2020 Sep 30. Annu Rev Control. 2020. PMID: 33020692 Free PMC article. - Impact of the H275Y and I223V Mutations in the Neuraminidase of the 2009 Pandemic Influenza Virus In Vitro and Evaluating Experimental Reproducibility.
Paradis EG, Pinilla LT, Holder BP, Abed Y, Boivin G, Beauchemin CA. Paradis EG, et al. PLoS One. 2015 May 20;10(5):e0126115. doi: 10.1371/journal.pone.0126115. eCollection 2015. PLoS One. 2015. PMID: 25992792 Free PMC article. - Energy Requirements for Loss of Viral Infectivity.
Rowell CER, Dobrovolny HM. Rowell CER, et al. Food Environ Virol. 2020 Dec;12(4):281-294. doi: 10.1007/s12560-020-09439-9. Epub 2020 Aug 5. Food Environ Virol. 2020. PMID: 32757142 Free PMC article.
References
- Beauchemin, C., J. Samuel, and J. Tuszynski. 2005. A simple cellular automaton model for influenza A viral infections. J. Theor. Biol. 232:223-234. - PubMed
- Bocharov, G. A., and A. A. Romanyukha. 1994. Mathematical model of antiviral immune response. III. Influenza A virus infection. J. Theor. Biol. 167:323-360. - PubMed
- Cella, M., F. Facchetti, A. Lanzavecchia, and M. Colonna. 2000. Plasmacytoid dendritic cells activated by influenza virus and CD40L drive a potent TH1 polarization. Nat. Immunol. 1:305-310. - PubMed
- Clarke, S. 1983. Physical defenses of the respiratory tract. Eur. J. Respir. Dis. Suppl. 126:27-30.
- Reference deleted.
Publication types
MeSH terms
Substances
Grants and funding
- N01 AI 50020/AI/NIAID NIH HHS/United States
- R37 AI028433/AI/NIAID NIH HHS/United States
- R01 AI028433/AI/NIAID NIH HHS/United States
- R01 RR006555/RR/NCRR NIH HHS/United States
- AI 28433/AI/NIAID NIH HHS/United States
- RR 06555/RR/NCRR NIH HHS/United States
- N01AI50020/AI/NIAID NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical