Winners don't punish - PubMed (original) (raw)
Winners don't punish
Anna Dreber et al. Nature. 2008.
Abstract
A key aspect of human behaviour is cooperation. We tend to help others even if costs are involved. We are more likely to help when the costs are small and the benefits for the other person significant. Cooperation leads to a tension between what is best for the individual and what is best for the group. A group does better if everyone cooperates, but each individual is tempted to defect. Recently there has been much interest in exploring the effect of costly punishment on human cooperation. Costly punishment means paying a cost for another individual to incur a cost. It has been suggested that costly punishment promotes cooperation even in non-repeated games and without any possibility of reputation effects. But most of our interactions are repeated and reputation is always at stake. Thus, if costly punishment is important in promoting cooperation, it must do so in a repeated setting. We have performed experiments in which, in each round of a repeated game, people choose between cooperation, defection and costly punishment. In control experiments, people could only cooperate or defect. Here we show that the option of costly punishment increases the amount of cooperation but not the average payoff of the group. Furthermore, there is a strong negative correlation between total payoff and use of costly punishment. Those people who gain the highest total payoff tend not to use costly punishment: winners don't punish. This suggests that costly punishment behaviour is maladaptive in cooperation games and might have evolved for other reasons.
Figures
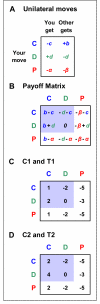
Figure 1. Payoff values
A: The game is formulated in terms of unilateral moves. There is the choice between cooperation, C, defection, D, and costly punishment, P. Cooperation means paying a cost, c, for the other person to get a benefit, b. Defection means earning a payoff, d, at a cost, d, for the other person. Punishment means paying a cost, α, for the other person to incur a cost, β. B: The payoff matrix is constructed from these unilateral moves. C and D: The actual payoff matrices of our experiments.
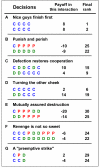
Figure 2. Games people played
There were 1230 pair-wise, repeated interactions each lasting between 1 and 9 rounds. Here are some examples (B, E and G are from T1, the others from T2.) The two players’ moves, the cumulative payoff of that interaction and the final rank of each player (sorted from highest to lowest payoff) are shown. A: All-out cooperation between two top-ranked players. B: Punish and perish. C: Defection for defection can sometimes restore cooperation. D: Turning the other cheek can also restore cooperation. E: Mutual punishment is mutual destruction. F: Punishment does not restore cooperation. Player 1 punishes a defection, which leads to mutual defection. Then player 1 is unsatisfied and deals out more punishment. G: “Guns don’t kill people, people kill people”. (Punishment itself is not destructive, only the people who use it.) Here, an unprovoked first strike destroys cooperation. The option to punish allows irrational people to inflict harm on the undeserving.
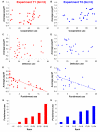
Figure 3. Punish and perish
In both treatments T1 (red) and T2 (blue), there is no correlation between average payoff per round and (i) cooperation use (Quantile regression; A, p = 0.33; B, p = 0.21) or (ii) defection use (C, p = 0.66; D, p = 0.36). However, there is a significant negative correlation between average payoff per round and punishment use in both treatments (E, slope = -0.042, p < 0.001; F, slope = -0.029, p = 0.015). Punishment use is the overriding determinant of payoff. G and H: Ranking players according to their total payoff shows a clear trend: players with lower rank (higher payoffs) punish less than players with higher rank (lower payoff).
Figure 4. Tit-for-tat prevails over costly punishment
Lower payoffs are correlated not only with punishment use, but specifically with choosing to punish after the opponent has defected. The probability of punishing immediately after a co-player’s defection is negatively correlated with the average payoff per round, both in T1 and T2 (Quantile regression; A, slope = -0.81, p < 0.001; B, slope = -0.94, p = 0.015). Thus, the lower payoffs of punishers were not caused by the bad luck of interacting with defectors. Winners use a tit-for-tat like approach (D for D), while losers use costly punishment (P for D).
Comment in
- Human behaviour: punisher pays.
Milinski M, Rockenbach B. Milinski M, et al. Nature. 2008 Mar 20;452(7185):297-8. doi: 10.1038/452297a. Nature. 2008. PMID: 18354472 No abstract available.
Similar articles
- Indirect reciprocity provides only a narrow margin of efficiency for costly punishment.
Ohtsuki H, Iwasa Y, Nowak MA. Ohtsuki H, et al. Nature. 2009 Jan 1;457(7225):79-82. doi: 10.1038/nature07601. Nature. 2009. PMID: 19122640 Free PMC article. - Third-party punishment as a costly signal of high continuation probabilities in repeated games.
Jordan JJ, Rand DG. Jordan JJ, et al. J Theor Biol. 2017 May 21;421:189-202. doi: 10.1016/j.jtbi.2017.04.004. Epub 2017 Apr 5. J Theor Biol. 2017. PMID: 28390842 - How costly punishment, diversity, and density of connectivity influence cooperation in a biological network.
Ezeigbo IC. Ezeigbo IC. Sci Rep. 2017 Dec 11;7(1):17319. doi: 10.1038/s41598-017-17481-0. Sci Rep. 2017. PMID: 29229960 Free PMC article. - Punishment and spite, the dark side of cooperation.
Jensen K. Jensen K. Philos Trans R Soc Lond B Biol Sci. 2010 Sep 12;365(1553):2635-50. doi: 10.1098/rstb.2010.0146. Philos Trans R Soc Lond B Biol Sci. 2010. PMID: 20679108 Free PMC article. Review. - A behavioral analysis of altruism.
Rachlin H, Locey M. Rachlin H, et al. Behav Processes. 2011 May;87(1):25-33. doi: 10.1016/j.beproc.2010.12.004. Epub 2010 Dec 22. Behav Processes. 2011. PMID: 21184815 Free PMC article. Review.
Cited by
- Low competitive status elicits aggression in healthy young men: behavioural and neural evidence.
Buades-Rotger M, Göttlich M, Weiblen R, Petereit P, Scheidt T, Keevil BG, Krämer UM. Buades-Rotger M, et al. Soc Cogn Affect Neurosci. 2021 Nov 15;16(11):1123-1137. doi: 10.1093/scan/nsab061. Soc Cogn Affect Neurosci. 2021. PMID: 33959776 Free PMC article. - Ripples in the pond: Evidence for contagious cooperative role modeling through moral elevation and calling in a small pre-study.
Zhang Q, Ma J, Wang Y, Lu X, Fan C. Zhang Q, et al. Front Psychol. 2022 Oct 20;13:1005772. doi: 10.3389/fpsyg.2022.1005772. eCollection 2022. Front Psychol. 2022. PMID: 36337499 Free PMC article. - Collective action and the detrimental side of punishment.
Shutters ST. Shutters ST. Evol Psychol. 2013 Apr 12;11(2):327-46. doi: 10.1177/147470491301100204. Evol Psychol. 2013. PMID: 23579191 Free PMC article. - Punitive preferences, monetary incentives and tacit coordination in the punishment of defectors promote cooperation in humans.
Diekmann A, Przepiorka W. Diekmann A, et al. Sci Rep. 2015 May 19;5:10321. doi: 10.1038/srep10321. Sci Rep. 2015. PMID: 25988875 Free PMC article. - The probabilistic pool punishment proportional to the difference of payoff outperforms previous pool and peer punishment.
Ohdaira T. Ohdaira T. Sci Rep. 2022 Apr 22;12(1):6604. doi: 10.1038/s41598-022-10582-5. Sci Rep. 2022. PMID: 35459880 Free PMC article.
References
- Trivers R. The evolution of reciprocal altruism. Q. Rev. Biol. 1971;46:35–57.
- Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. - PubMed
- Fudenberg D, Maskin E. Evolution and cooperation in noisy repeated games. Am. Econ. Rev. 1990;80:274–279.
- Nowak MA, Sigmund K. Tit for tat in heterogeneous populations. Nature. 1992;355:250–253.
- Binmore K, Samuelson L. Evolutionary stability in repeated games played by finite automata. J. of Econ. Theory. 1992;57:278–305.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources