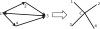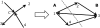Discovering pathways by orienting edges in protein interaction networks - PubMed (original) (raw)
Discovering pathways by orienting edges in protein interaction networks
Anthony Gitter et al. Nucleic Acids Res. 2011 Mar.
Abstract
Modern experimental technology enables the identification of the sensory proteins that interact with the cells' environment or various pathogens. Expression and knockdown studies can determine the downstream effects of these interactions. However, when attempting to reconstruct the signaling networks and pathways between these sources and targets, one faces a substantial challenge. Although pathways are directed, high-throughput protein interaction data are undirected. In order to utilize the available data, we need methods that can orient protein interaction edges and discover high-confidence pathways that explain the observed experimental outcomes. We formalize the orientation problem in weighted protein interaction graphs as an optimization problem and present three approximation algorithms based on either weighted Boolean satisfiability solvers or probabilistic assignments. We use these algorithms to identify pathways in yeast. Our approach recovers twice as many known signaling cascades as a recent unoriented signaling pathway prediction technique and over 13 times as many as an existing network orientation algorithm. The discovered paths match several known signaling pathways and suggest new mechanisms that are not currently present in signaling databases. For some pathways, including the pheromone signaling pathway and the high-osmolarity glycerol pathway, our method suggests interesting and novel components that extend current annotations.
Figures
Figure 1.
An example of the MAX-DI-CUT to MEO transformation. The MEO graph has the same vertices as the MAX-DI-CUT graph plus an additional center vertex, to which all other vertices are connected. The MAX-DI-CUT edges are used to define the MEO source–target pairs.
Figure 2.
Mapping an orientation of the MEO instance back to a directed cut. An orientation in the MEO problem uniquely defines a cut in the MAX-DI-CUT instance. The number of satisfied paths in the MEO instance is identical to the number of directed edges from A to B.
Figure 3.
Fraction of the objective function upper bound achieved on instances with simulated sources and targets. After local search, all approximation algorithms perform much better than the MAX-k-CSP theoretical guarantee on instances with simulated source–target pairs and find orientations whose objective function values are virtually indistinguishable. The number of undirected paths includes all paths from a source to a target before the network is oriented. The _y_-axis plots the ratio achieved by each algorithm, which is the score of the orientation returned by the algorithm divided by the upper bound on the optimal objective function value. For each instance, there are six points (one for each algorithm with and without local search) that have the same x-coordinate, the number of undirected paths, and different y-coordinates, the ratios achieved. Instances have been ordered along the _x_-axis by the number of distinct source–target paths in the network before orientation, which is a coarse indication of the difficulty of the instance.
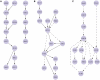
Figure 4.
The top-ranked pathways discovered by the random orientation plus local search algorithm. Solid edges were present in the gold standard and dashed edges were absent or oriented in the opposite direction. (A) Pathways that are completely contained within a known gold standard pathway. (B) Pathways that partially overlap a gold standard path but contain new edges as well. (C) Pathways that do not have any edges in common with our set of gold standard pathways. Images were generated with Cytoscape (
) and do not contain all of the top-ranked paths per category but rather a highly overlapping subset.
Similar articles
- Orienting Conflicted Graph Edges Using Genetic Algorithms to Discover Pathways in Protein-Protein Interaction Networks.
Iqbal S, Halim Z. Iqbal S, et al. IEEE/ACM Trans Comput Biol Bioinform. 2021 Sep-Oct;18(5):1970-1985. doi: 10.1109/TCBB.2020.2966703. Epub 2021 Oct 7. IEEE/ACM Trans Comput Biol Bioinform. 2021. PMID: 31944985 - Optimally orienting physical networks.
Silverbush D, Elberfeld M, Sharan R. Silverbush D, et al. J Comput Biol. 2011 Nov;18(11):1437-48. doi: 10.1089/cmb.2011.0163. Epub 2011 Oct 14. J Comput Biol. 2011. PMID: 21999286 - Efficient algorithms for detecting signaling pathways in protein interaction networks.
Scott J, Ideker T, Karp RM, Sharan R. Scott J, et al. J Comput Biol. 2006 Mar;13(2):133-44. doi: 10.1089/cmb.2006.13.133. J Comput Biol. 2006. PMID: 16597231 - A systems approach to discovering signaling and regulatory pathways--or, how to digest large interaction networks into relevant pieces.
Ideker T. Ideker T. Adv Exp Med Biol. 2004;547:21-30. doi: 10.1007/978-1-4419-8861-4_3. Adv Exp Med Biol. 2004. PMID: 15230090 Review. - Biological Network Inference and analysis using SEBINI and CABIN.
Taylor R, Singhal M. Taylor R, et al. Methods Mol Biol. 2009;541:551-76. doi: 10.1007/978-1-59745-243-4_24. Methods Mol Biol. 2009. PMID: 19381531 Review.
Cited by
- Linking the signaling cascades and dynamic regulatory networks controlling stress responses.
Gitter A, Carmi M, Barkai N, Bar-Joseph Z. Gitter A, et al. Genome Res. 2013 Feb;23(2):365-76. doi: 10.1101/gr.138628.112. Epub 2012 Oct 11. Genome Res. 2013. PMID: 23064748 Free PMC article. - Stems cells, big data and compendium-based analyses for identifying cell types, signalling pathways and gene regulatory networks.
Kabir MH, O'Connor MD. Kabir MH, et al. Biophys Rev. 2019 Feb;11(1):41-50. doi: 10.1007/s12551-018-0486-4. Epub 2019 Jan 25. Biophys Rev. 2019. PMID: 30684132 Free PMC article. Review. - An optimization framework for network annotation.
Patkar S, Sharan R. Patkar S, et al. Bioinformatics. 2018 Jul 1;34(13):i502-i508. doi: 10.1093/bioinformatics/bty236. Bioinformatics. 2018. PMID: 29949973 Free PMC article. - Multi-label multi-instance transfer learning for simultaneous reconstruction and cross-talk modeling of multiple human signaling pathways.
Mei S, Zhu H. Mei S, et al. BMC Bioinformatics. 2015 Dec 30;16:417. doi: 10.1186/s12859-015-0841-4. BMC Bioinformatics. 2015. PMID: 26718335 Free PMC article. - Pathways on demand: automated reconstruction of human signaling networks.
Ritz A, Poirel CL, Tegge AN, Sharp N, Simmons K, Powell A, Kale SD, Murali TM. Ritz A, et al. NPJ Syst Biol Appl. 2016 Mar 3;2:16002. doi: 10.1038/npjsba.2016.2. eCollection 2016. NPJ Syst Biol Appl. 2016. PMID: 28725467 Free PMC article.
References
- Bar-Joseph Z, Gerber GK, Lee TI, Rinaldi NJ, Yoo JY, Robert F, Gordon DB, Fraenkel E, Jaakkola TS, Young RA, et al. Computational discovery of gene modules and regulatory networks. Nat. Biotechnol. 2003;21:1337–1342. - PubMed
- Segal E, Shapira M, Regev A, Pe’er D, Botstein D, Koller D, Friedman N. Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat. Genet. 2003;34:166–176. - PubMed
- Covert MW, Knight EM, Reed JL, Herrgard MJ, Palsson BO. Integrating high-throughput and computational data elucidates bacterial networks. Nature. 2004;429:92–96. - PubMed
- Fischer E, Sauer U. Large-scale in vivo flux analysis shows rigidity and suboptimal performance of Bacillus subtilis metabolism. Nat. Genet. 2005;37:636–640. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases