Using observation-level random effects to model overdispersion in count data in ecology and evolution - PubMed (original) (raw)

Using observation-level random effects to model overdispersion in count data in ecology and evolution

Xavier A Harrison. PeerJ. 2014.

Abstract

Overdispersion is common in models of count data in ecology and evolutionary biology, and can occur due to missing covariates, non-independent (aggregated) data, or an excess frequency of zeroes (zero-inflation). Accounting for overdispersion in such models is vital, as failing to do so can lead to biased parameter estimates, and false conclusions regarding hypotheses of interest. Observation-level random effects (OLRE), where each data point receives a unique level of a random effect that models the extra-Poisson variation present in the data, are commonly employed to cope with overdispersion in count data. However studies investigating the efficacy of observation-level random effects as a means to deal with overdispersion are scarce. Here I use simulations to show that in cases where overdispersion is caused by random extra-Poisson noise, or aggregation in the count data, observation-level random effects yield more accurate parameter estimates compared to when overdispersion is simply ignored. Conversely, OLRE fail to reduce bias in zero-inflated data, and in some cases increase bias at high levels of overdispersion. There was a positive relationship between the magnitude of overdispersion and the degree of bias in parameter estimates. Critically, the simulations reveal that failing to account for overdispersion in mixed models can erroneously inflate measures of explained variance (r (2)), which may lead to researchers overestimating the predictive power of variables of interest. This work suggests use of observation-level random effects provides a simple and robust means to account for overdispersion in count data, but also that their ability to minimise bias is not uniform across all types of overdispersion and must be applied judiciously.

Keywords: Explained variance; Generalized linear mixed models; Observation-level random effect; Poisson-lognormal models; Quasi-Poisson; r-squared.

PubMed Disclaimer

Figures

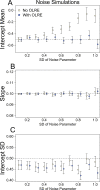
Figure 1

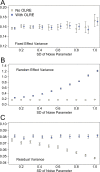
Figure 1. Model parameters for the intercept mean (A), slope of the effect of body size (B) and intercept standard deviation (C) generated under various levels of overdispersion for the noise simulations.

Light circles represent the mean values of the Naive models, where overdispersion was ignored. Blue circles represent the models containing observation-level random effects. Error bars are 95% confidence intervals of the mean as estimated by bootstrapping. Dashed horizontal lines denote the true (simulated) parameter values.

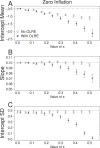
Figure 2

Figure 2. Parameters for the intercept mean (A), slope of the effect of body size (B) and intercept standard deviation (C) generated under various levels of overdispersion for the Zero-Inflation simulations.

Light circles represent the mean values of the Naive models, where overdispersion was ignored. Blue circles represent the models containing observation-level random effects. Error bars are 95% confidence intervals of the mean as estimated by bootstrapping. Dashed horizontal lines denote the true (simulated) parameter values.

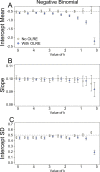
Figure 3

Figure 3. Parameters for the intercept mean (A), slope of the effect of body size (B) and intercept standard deviation (C) generated under various levels of overdispersion for the negative binomial simulations.

Light circles represent the mean values of the Naive models, where overdispersion was ignored. Blue circles represent the models containing observation-level random effects. Error bars are 95% confidence intervals of the mean as estimated by bootstrapping. Dashed horizontal lines denote the true (simulated) parameter values.

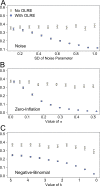
Figure 4

Figure 4. Marginal _r_2 values of models generated under 3 scenarios of overdispersion: (A) extra-Poisson noise; (B) zero-inflated data; and (C) data generated from a negative binomial distribution.

Moving from left to right on the x axes corresponds to increasing levels of overdispersion in the models. Light circles represent the mean values of the Naive models, where overdispersion was ignored. Blue circles represent the models containing observation-level random effects. Error bars are 95% confidence intervals of the mean as estimated by bootstrapping. Ignoring overdispersion under all three scenarios resulted in greatly inflated estimates of the proportion of explained variance relative to where overdispersion was taken into account.

Figure 5

Figure 5. The three components of variance used to calculate the _r_2 metrics proposed by Nakagawa & Schielzeth (2013) for the noise simulation datasets at various levels of overdispersion.

Light circles represent the mean values of the Naive models, where overdispersion was ignored. Blue circles represent the models containing observation-level random effects. Error bars are 95% confidence intervals of the mean as estimated by bootstrapping.

Similar articles

Cited by

References

    1. Bates D, Maechler M, Bolker B, Walker S. lme4: linear mixed-effects models using Eigen and S4. (R package version 1.1-6) 2014 Available at http://CRAN.R-project.org/package=lme4 .
    1. Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, White JSS. Generalized linear mixed models: a practical guide for ecology and evolution. Trends in Ecology & Evolution. 2009;24:127–135. doi: 10.1016/j.tree.2008.10.008. - DOI - PubMed
    1. Crawley MJ. The R book. United Kingdom: John Wiley & Sons Ltd; 2007.
    1. Elston DA, Moss R, Bouliner T, Arrowsmith C, Lambin X. Analysis of aggregation, a worked example: number of ticks on red grouse. Parasitology. 2001;122:563–569. doi: 10.1017/S0031182001007740. - DOI - PubMed
    1. Fournier DA, Skaug HJ, Ancheta J, Ianelli J, Magnusson A, Maunder M, Nielsen A, Sibert J. AD Model Builder: using automatic differentiation for statistical inference of highly parameterised complex non-linear models. Optimisation Methods & Software. 2012;27:233–249. doi: 10.1080/10556788.2011.597854. - DOI

LinkOut - more resources