The total consumption model applied to gambling: Empirical validity and implications for gambling policy - PubMed (original) (raw)
Review
The total consumption model applied to gambling: Empirical validity and implications for gambling policy
Ingeborg Rossow. Nordisk Alkohol Nark. 2019 Apr.
Abstract
Aim: The total consumption model (TCM) originates from studies of the distribution of alcohol consumption and posits that there is a strong association between the total consumption and the prevalence of excessive/harmful consumption in a population. The policy implication of the TCM is that policy measures which effectively lead to a reduction of the total consumption, will most likely also reduce the extent of harmful consumption and related harms. Problem gambling constitutes a public health issue and more insight into problem gambling at the societal level and a better understanding of how public policies may impact on the harm level, are strongly needed. The aim of this study was to review the literature pertaining to empirical validity of the TCM with regard to gambling behaviour and problem gambling and, on the basis of the literature review, to discuss the policy implications of the TCM.
Methods: The study is based on a literature mapping through systematic searches in literature databases, and forward and backward reference searches.
Results: The literature searches identified a total of 12 empirical studies that examined the total consumption model or provided relevant data. All but one of these studies found empirical support for the TCM; that is, a positive association between population gambling mean and prevalence of excessive or problem gambling. Such associations were found both with cross-sectional data and with longitudinal data.
Conclusion: There is a small but fairly consistent literature lending empirical support to the total consumption model. An important policy implication is that interventions which are successful in reducing overall gambling are likely also to reduce problem gambling incidence.
Keywords: distribution; gambling; gambling policy; literature review; problem gambling.
© The Author(s) 2018.
Conflict of interest statement
Declaration of conflicting interests: The author declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Figures
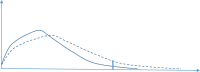
Figure 1.
Consumption distribution curves for two samples with different means Distribution of consumption is shown as proportion of population (Y-axis) by consumption units (X-axis). The distribution curve for Sample 1 (presented with a solid line) has a lower mean than the distribution curve for Sample 2 (presented with a dotted line). The fraction of the population with excessive consumption (consuming above the value marked with a vertical line) is represented by the area under the distribution curve, and this fraction is clearly larger for Sample 2 than for Sample 1.
Similar articles
- Gambling consumption and harm: a systematic review of the evidence.
Kesaite V, Wardle H, Rossow I. Kesaite V, et al. Addict Res Theory. 2023 Aug 2;32(3):194-203. doi: 10.1080/16066359.2023.2238608. eCollection 2024. Addict Res Theory. 2023. PMID: 38774110 Free PMC article. Review. - Availability restrictions and mandatory precommitment in land-based gambling: effects on online substitutes and total consumption in longitudinal sales data.
Marionneau V, Selin J, Impinen A, Roukka T. Marionneau V, et al. BMC Public Health. 2024 Mar 14;24(1):809. doi: 10.1186/s12889-024-18325-z. BMC Public Health. 2024. PMID: 38486180 Free PMC article. - The changing epidemiology of gambling disorder and gambling-related harm: public health implications.
Abbott MW. Abbott MW. Public Health. 2020 Jul;184:41-45. doi: 10.1016/j.puhe.2020.04.003. Epub 2020 Apr 30. Public Health. 2020. PMID: 32402593 Review. - Women and gambling-related harm: a narrative literature review and implications for research, policy, and practice.
McCarthy S, Thomas SL, Bellringer ME, Cassidy R. McCarthy S, et al. Harm Reduct J. 2019 Mar 4;16(1):18. doi: 10.1186/s12954-019-0284-8. Harm Reduct J. 2019. PMID: 30832672 Free PMC article. Review. - What is the evidence that advertising policies could have an impact on gambling-related harms? A systematic umbrella review of the literature.
McGrane E, Wardle H, Clowes M, Blank L, Pryce R, Field M, Sharpe C, Goyder E. McGrane E, et al. Public Health. 2023 Feb;215:124-130. doi: 10.1016/j.puhe.2022.11.019. Epub 2023 Jan 26. Public Health. 2023. PMID: 36725155
Cited by
- Gambling consumption and harm: a systematic review of the evidence.
Kesaite V, Wardle H, Rossow I. Kesaite V, et al. Addict Res Theory. 2023 Aug 2;32(3):194-203. doi: 10.1080/16066359.2023.2238608. eCollection 2024. Addict Res Theory. 2023. PMID: 38774110 Free PMC article. Review. - Tracking online searches for gambling activities and operators in the United Kingdom during the COVID-19 pandemic: A Google Trends™ analysis.
Houghton S, Boy F, Bradley A, James R, Wardle H, Dymond S. Houghton S, et al. J Behav Addict. 2023 Oct 12;12(4):983-991. doi: 10.1556/2006.2023.00055. Print 2023 Dec 22. J Behav Addict. 2023. PMID: 38141072 Free PMC article. - Gambling harm prevention and harm reduction in online environments: a call for action.
Marionneau V, Ruohio H, Karlsson N. Marionneau V, et al. Harm Reduct J. 2023 Jul 22;20(1):92. doi: 10.1186/s12954-023-00828-4. Harm Reduct J. 2023. PMID: 37481649 Free PMC article. Review. - Changes in sports gambling behavior during the COVID-19 pandemic in Canada.
Otis E, Kim AJ, Stewart SH, Sherry SB, Yakovenko I. Otis E, et al. Front Psychiatry. 2022 Nov 9;13:1018234. doi: 10.3389/fpsyt.2022.1018234. eCollection 2022. Front Psychiatry. 2022. PMID: 36440391 Free PMC article. - An Empirical Attempt to Operationalize Chasing Losses in Gambling Utilizing Account-Based Player Tracking Data.
Auer M, Griffiths MD. Auer M, et al. J Gambl Stud. 2023 Dec;39(4):1547-1561. doi: 10.1007/s10899-022-10144-4. Epub 2022 Jul 14. J Gambl Stud. 2023. PMID: 35834118 Free PMC article.
References
- Abbott M. (2006). Do EGMs and problem gambling go together like a horse and carriage? Gambling Research, 18(1), 7–38.
- Bramness J. G., Rossow I. (2010). Can the total consumption of a medicinal drug be used as an indicator of excessive use? The case of carisoprodol. Drugs: Education, Prevention, and Policy, 17(2), 168–180. doi:10.3109/09687630903264278
- Govoni R. J. (2000). Gambling behaviour and the distribution of alcohol consumption model (PhD thesis). University of Windsor, Canada: Retrieved from https://scholar.uwindsor.ca/etd/2186
- Grun L., McKeigue P. (2000). Prevalence of excessive gambling before and after introduction of a national lottery in the United Kingdom: Another example of the single distribution theory. Addiction, 95(6), 959–966. doi:10.1046/j.1360-0443.2000.95695912.x - PubMed
- Hansen M. B., Rossow I. (2008). Adolescent gambling and problem gambling: Does the total consumption model apply? Journal of Gambling Studies, 24(2), 135–149. doi:10.1007/s10899-007-9082-4 - PubMed
Publication types
LinkOut - more resources
Full Text Sources