Storing Hierarchical Data in a Database — SitePoint (original) (raw)
Key Takeaways
- Storing hierarchical data in a database can be achieved using two major approaches: the adjacency list model and the modified preorder tree traversal algorithm. The adjacency list model is more elegant and simple, but can be slow and inefficient for large trees due to the use of recursion.
- In the adjacency list method, each node in the hierarchy has a ‘parent’ saved. This approach allows for easy iteration through the tree using a simple function, but can be slow when dealing with large trees due to the need for one database query for each node in the tree.
- Despite its simplicity, the adjacency list model has downsides. It is slow and inefficient in most programming languages, mainly due to recursion. Also, most languages are not designed for recursive functions, thus for a tree with multiple levels, multiple instances of the function will be running simultaneously, making it slow for large trees.
This article was written in 2003 and remains one of our most popular posts. If you’re keen to learn more about mastering database management, you may find this recent article on MySQL of great interest.
Whether you want to build your own forum, publish the messages from a mailing list on your Website, or write your own cms: there will be a moment that you’ll want to store hierarchical data in a database. And, unless you’re using a XML-like database, tables aren’t hierarchical; they’re just a flat list. You’ll have to find a way to translate the hierarchy in a flat file.
Storing trees is a common problem, with multiple solutions. There are two major approaches: the adjacency list model, and the modified preorder tree traversal algorithm.
In this article, we’ll explore these two methods of saving hierarchical data. I’ll use the tree from a fictional online food store as an example. This food store organizes its food by category, by colour and by type. The tree looks like this:
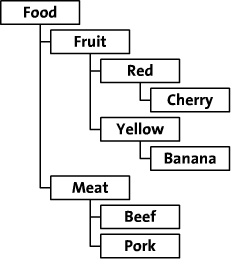
This article contains a number of code examples that show how to save and retrieve data. Because I use that language myself, and many other people use or know that language too, I chose to write the examples in PHP. You can probably easily translate them to your own language of choice.
The Adjacency List Model
The first, and most elegant, approach we’ll try is called the ‘adjacency list model’ or the ‘recursion method’. It’s an elegant approach because you’ll need just one, simple function to iterate through your tree. In our food store, the table for an adjacency list looks like this:
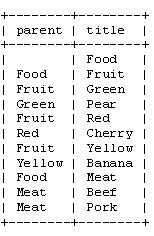
As you can see, in the adjacency list method, you save the ‘parent’ of each node. We can see that ‘Pear’ is a child of ‘Green’, which is a child of ‘Fruit’ and so on. The root node, ‘Food’, doesn’t have a parent value. For simplicity, I’ve used the ‘title’ value to identify each node. Of course, in a real database, you’d use the numerical id of each node.
Give Me the Tree
Now that we’ve inserted our tree in the database, it’s time to write a display function. This function will have to start at the root node — the node with no parent — and should then display all children of that node. For each of these children, the function should retrieve and display all the child nodes of that child. For these children, the function should again display all children, and so on.
As you might have noticed, there’s a regular pattern in the description of this function. We can simply write one function, which retrieves the children of a certain parent node. That function should then start another instance of itself for each of these children, to display all their children. This is the recursive mechanism that gives the ‘recursion method’ its name.
<?php
// $parent is the parent of the children we want to see
// $level is increased when we go deeper into the tree,
// used to display a nice indented tree
function display_children($parent, $level) {
// retrieve all children of $parent
$result = mysql_query('SELECT title FROM tree '.
'WHERE parent="'.$parent.'";');
// display each child
while ($row = mysql_fetch_array($result)) {
// indent and display the title of this child
echo str_repeat(' ',$level).$row['title']."n";
// call this function again to display this
// child's children
display_children($row['title'], $level+1);
}
}
?>To display our whole tree, we’ll run the function with an empty string as $parent and $level = 0: display_children('',0); For our food store tree, the function returns:
Food
Fruit
Red
Cherry
Yellow
Banana
Meat
Beef
PorkNote that if you just want to see a subtree, you can tell the function to start with another node. For example, to display the ‘Fruit’ subtree, you would run display_children('Fruit',0);
The Path to a Node
With almost the same function, it’s possible to look up the path to a node if you only know the name or id of that node. For instance, the path to ‘Cherry’ is ‘Food’ > ‘Fruit’ > ‘Red’. To get this path, our function will have to start at the deepest level: ‘Cherry’. It then looks up the parent of this node and adds this to the path. In our example, this would be ‘Red’. If we know that ‘Red’ is the parent of ‘Cherry’, we can calculate the path to ‘Cherry’ by using the path to ‘Red’. And that’s given by the function we’ve just used: by recursively looking up parents, we’ll get the path to any node in the tree.
<?php
// $node is the name of the node we want the path of
function get_path($node) {
// look up the parent of this node
$result = mysql_query('SELECT parent FROM tree '.
'WHERE title="'.$node.'";');
<span class="katex"><span class="katex-mathml"><math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>r</mi><mi>o</mi><mi>w</mi><mo>=</mo><mi>m</mi><mi>y</mi><mi>s</mi><mi>q</mi><msub><mi>l</mi><mi>f</mi></msub><mi>e</mi><mi>t</mi><mi>c</mi><msub><mi>h</mi><mi>a</mi></msub><mi>r</mi><mi>r</mi><mi>a</mi><mi>y</mi><mo stretchy="false">(</mo></mrow><annotation encoding="application/x-tex">row = mysql_fetch_array(</annotation></semantics></math></span><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">ro</span><span class="mord mathnormal" style="margin-right:0.02691em;">w</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.0361em;vertical-align:-0.2861em;"></span><span class="mord mathnormal">m</span><span class="mord mathnormal">ys</span><span class="mord mathnormal" style="margin-right:0.03588em;">q</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3361em;"><span style="top:-2.55em;margin-left:-0.0197em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.10764em;">f</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.2861em;"><span></span></span></span></span></span></span><span class="mord mathnormal">e</span><span class="mord mathnormal">t</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal">h</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">a</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.02778em;">rr</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mopen">(</span></span></span></span>result);
// save the path in this array
$path = array();
// only continue if this $node isn't the root node
// (that's the node with no parent)
if ($row['parent']!='') {
// the last part of the path to $node, is the name
// of the parent of $node
<span class="katex"><span class="katex-mathml"><math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>p</mi><mi>a</mi><mi>t</mi><mi>h</mi><mo stretchy="false">[</mo><mo stretchy="false">]</mo><mo>=</mo></mrow><annotation encoding="application/x-tex">path[] = </annotation></semantics></math></span><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal">p</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">h</span><span class="mopen">[</span><span class="mclose">]</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span></span></span></span>row['parent'];
// we should add the path to the parent of this node
// to the path
<span class="katex"><span class="katex-mathml"><math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>p</mi><mi>a</mi><mi>t</mi><mi>h</mi><mo>=</mo><mi>a</mi><mi>r</mi><mi>r</mi><mi>a</mi><msub><mi>y</mi><mi>m</mi></msub><mi>e</mi><mi>r</mi><mi>g</mi><mi>e</mi><mo stretchy="false">(</mo><mi>g</mi><mi>e</mi><msub><mi>t</mi><mi>p</mi></msub><mi>a</mi><mi>t</mi><mi>h</mi><mo stretchy="false">(</mo></mrow><annotation encoding="application/x-tex">path = array_merge(get_path(</annotation></semantics></math></span><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">p</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">h</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.0361em;vertical-align:-0.2861em;"></span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.02778em;">rr</span><span class="mord mathnormal">a</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">m</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">e</span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">e</span><span class="mord"><span class="mord mathnormal">t</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">p</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.2861em;"><span></span></span></span></span></span></span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">h</span><span class="mopen">(</span></span></span></span>row['parent']), $path);
}
// return the path
return $path;
}
?>This function now returns the path to a given node. It returns that path as an array, so to display the path we can use print_r(get_path('Cherry')); If you do this for ‘Cherry’, you’ll see:
Array
(
[0] => Food
[1] => Fruit
[2] => Red
)Disadvantages
As we’ve just seen, this is a great method. It’s easy to understand, and the code we need is simple, too. What then, are the downsides of the adjacency list model? In most programming languages, it’s slow and inefficient. This is mainly caused by the recursion. We need one database query for each node in the tree.
As each query takes some time, this makes the function very slow when dealing with large trees.
The second reason this method isn’t that fast, is the programming language you’ll probably use. Unlike languages such as Lisp, most languages aren’t designed for recursive functions. For each node, the function starts another instance of itself. So, for a tree with four levels, you’ll be running four instances of the function at the same time. As each function occupies a slice of memory and takes some time to initiate, recursion is very slow when applied to large trees.
Frequently Asked Questions on Hierarchical Data in Databases
What is the Adjacency List Model in Hierarchical Data?
The Adjacency List Model is a common method for storing hierarchical data in a database. In this model, each record has a pointer to its parent record in the hierarchy. This model is simple and easy to understand, but it can be inefficient for querying large amounts of data because it requires multiple self-joins to retrieve an entire hierarchy.
How does the Path Enumeration Model work?
The Path Enumeration Model is another method for storing hierarchical data. In this model, each record stores the path from the root of the hierarchy to that record. This makes querying the data more efficient because you can retrieve an entire hierarchy with a single query. However, this model can be more complex to maintain because changes to the hierarchy require updating multiple records.
What is the Nested Set Model?
The Nested Set Model is a more complex method for storing hierarchical data. In this model, each record has two additional fields that represent the left and right boundaries of a nested set of records. This model can be very efficient for querying hierarchical data, but it can be more complex to maintain because changes to the hierarchy require updating multiple records.
How does the Closure Table Model work?
The Closure Table Model is a method for storing hierarchical data that uses a separate table to store the relationships between records. This model can be very efficient for querying hierarchical data, and it can handle changes to the hierarchy more easily than the Nested Set Model. However, it requires additional storage space for the closure table.
What is the Materialized Path Model?
The Materialized Path Model is a method for storing hierarchical data that combines aspects of the Adjacency List Model and the Path Enumeration Model. In this model, each record stores the path from the root of the hierarchy to that record, as well as a pointer to its parent record. This model can be efficient for querying hierarchical data, and it can handle changes to the hierarchy more easily than the Nested Set Model.
How can I choose the best model for my hierarchical data?
The best model for your hierarchical data depends on the specific requirements of your application. If you need to query large amounts of data efficiently, you might choose the Nested Set Model or the Closure Table Model. If you need to handle changes to the hierarchy frequently, you might choose the Adjacency List Model or the Materialized Path Model.
What are the challenges of storing hierarchical data in a relational database?
Storing hierarchical data in a relational database can be challenging because relational databases are designed to store flat, tabular data. Hierarchical data, on the other hand, has a tree-like structure that can be difficult to represent in a flat table. This can make querying and maintaining the data more complex.
Can NoSQL databases handle hierarchical data better than relational databases?
NoSQL databases, such as MongoDB and CouchDB, can handle hierarchical data more naturally than relational databases because they can store nested data structures. However, NoSQL databases have their own set of challenges, such as lack of standardization and potential issues with data consistency.
How can I query hierarchical data efficiently?
Querying hierarchical data efficiently requires careful design of your database schema and your queries. Depending on the model you choose, you might need to use self-joins, recursive queries, or additional tables to retrieve the data you need. Indexing your data properly can also improve query performance.
How can I maintain hierarchical data in a database?
Maintaining hierarchical data in a database requires careful management of the relationships between records. Depending on the model you choose, you might need to update multiple records when you insert, update, or delete a record. Using database transactions can help ensure that your data remains consistent.