Gibbs Phenomenon (original) (raw)
In this page, we will study what happens to the convergence of the Fourier series for a piecewise smooth function. A piecewise smooth function is a function defined over an interval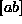 
which is continuous along with its first derivative except for a finite number of first-order discontinuity points (jumps); the left and right limits for the function and its first derivative at the discontinuity points must exist.
An example of this is the sawtooth function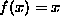 
,
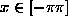, extended periodically on the real line; this function is discontinuous at 
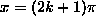for all interger values of k.
Let us define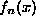 
as the sum of the fist n Fourier series terms for the function 
:
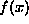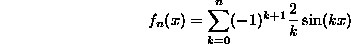
The interactive plot above displays the function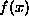 
(green line) and its Fourier series approximation 
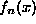(red line). You can explore what happens for different values of nby moving the slider called "partials". Use the mouse's scroll wheel to zoom and drag the plot to look at the details around a discontinuity point.
After playing a while, you should have noted the following facts:
- The Fourier series approximation displays an overshoot in the left-sided interval of the discontinuity (and a symmetric undershoot in the right-sided interval).
- While the convergence of the Fourier series to the sawtooth function improves anywhere else, the height of the overshoot does not decrease with augmenting the number of terms.
This behavior is called Gibbs Phenomenon. It shows that the Fourier series does not converge uniformly to a discontinuos function in an arbitrary small interval of the discontinuity point. Formally, the following theorem can be proven [1, pag. 63,]:
Interestingly, the the overshoot factor depends only on the type of discontinuity and not on the values of the function.
The Gibbs phenomenon has interesting physical consequences. Consider an electric circuit in which by means of a switch, an arbitrarily fast voltage transition is created. The response of the linear components of the circuit will exhibit an overshoot, which could be potentially disruptive.
Paolo Prandoni Sun Jun 1 19:32:27 MET DST 1997