Euclid's Elements, Book I, Definition 8 (original) (raw)
A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
Guide
The concept of angle is a very important concept for all of Greek geometry. Many of the propositions require angles even for their statements.
The two lines are meant to emanate from the same point; two intersecting lines will actually make four angles.
The concept is also a difficult one, and, surprisingly, broader than our modern concept of angle.
| As can be seen from the next definition of rectilinear angle, angles do not have to have straight sides; they can have curves as sides. The size of the angle does not depend on the length of the sides, but is determined only by how the two sides meet. In the Elements nearly all the angles are rectilinear, but angles with curved sides appear in proposition III.16. In that proposition, a so-called horn angle CAE is described as the angle between a circle and a straight tangent line and is shown to be smaller than any rectilinear angle FAE. Even though the curved side of the horn angle extends beyond any rectilinear angle, it is considered to be smaller since near the vertex A of the angle, the curvilinear angle CAE is entirely contained in the rectilinear angle FAE. Thus, an angle doesn’t have an extent. | 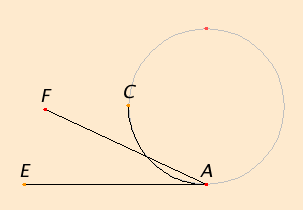 |
|---|