Euclid's Elements, Book I, Proposition 13 (original) (raw)
If a straight line stands on a straight line, then it makes either two right angles or angles whose sum equals two right angles.
Let any straight line AB standing on the straight line CD make the angles CBA and ABD.
I say that either the angles CBA and ABD are two right angles or their sum equals two right angles.
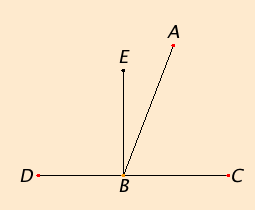
Now, if the angle CBA equals the angle ABD, then they are two right angles.
But, if not, draw BE from the point B at right angles to CD. Therefore the angles CBE and EBD are two right angles.
Since the angle CBE equals the sum of the two angles CBA and ABE, add the angle EBD to each, therefore the sum of the angles CBE and EBD equals the sum of the three angles CBA, ABE, and EBD.
Again, since the angle DBA equals the sum of the two angles DBE and EBA, add the angle ABC to each, therefore the sum of the angles DBA and ABC equals the sum of the three angles DBE, EBA, and ABC.
But the sum of the angles CBE and EBD was also proved equal to the sum of the same three angles, and things which equal the same thing also equal one another, therefore the sum of the angles CBE and EBD also equals the sum of the angles DBA and ABC. But the angles CBE and EBD are two right angles, therefore the sum of the angles DBA and ABC also equals two right angles.
Therefore if a straight line stands on a straight line, then it makes either two right angles or angles whose sum equals two right angles.
Q.E.D.
But that’s not the only addition that occurs here. Euclid also says that the sum of the angles CBE and EBD equals the sum of the three angles CBA, ABE, and EBD. That sum being mentioned is a straight angle, which is not to be considered as an angle according to Euclid. It is a formal sum equal to two right angles. In other propositions formal sums of four right angles occur. These and larger formal sums are not angles themselves, merely sums of angles. Only if an angle sum is less than two right angles can it be identified with a single angle.