Euclid's Elements, Book XI, Proposition 9 (original) (raw)

Straight lines which are parallel to the same straight line but do not lie in the same plane with it are also parallel to each other.

Let each of the straight lines AB and CD be parallel to EF, but not in the same plane with it.

I say that AB is parallel to CD.

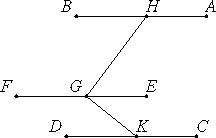
Let a point G be taken at random on EF, and from it draw GH in the plane through EF and AB at right angles to EF, and GK in the plane through EF and CD again at right angles to EF.

Now, since EF is at right angles to each of the straight lines GH and GK, therefore EF is also at right angles to the plane through GH and GK.

And EF is parallel to AB, therefore AB is also at right angles to the plane through HG and GK.

For the same reason CD is also at right angles to the plane through HG and GK. Therefore each of the straight lines AB and CD is at right angles to the plane through HG and GK.

But if two straight lines are at right angles to the same plane, then the straight lines are parallel. Therefore AB is parallel to CD.

Therefore, straight lines which are parallel to the same straight line but do not lie in the same plane with it are also parallel to each other.

Q.E.D.