Многочлен Лагранжа | это... Что такое Многочлен Лагранжа? (original) (raw)

Многочлен Лагранжа

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел 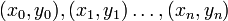$(x_0, y_0), (x_1, y_1)\dots ,(x_n, y_n)$ , где все x i различны, существует единственный многочлен L(x) степени не более n, для которого L(x i) = y i.

В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Содержание

1 Определение
2 Применения
- 2.1 Для случая равномерного распределения по отрезку узлов интерполяции
3 Внешние ссылки

Определение

Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xi

Лагранж предложил способ вычисления таких многочленов:

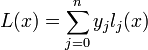
$L(x) = \sum_{j=0}^n y_j l_j(x)$

где базисные полиномы определяются по формуле:

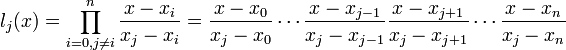
$l_j(x)=\prod_{i=0, j\neq i}^{n} \frac{x-x_i}{x_j-x_i} = \frac{x-x_0}{x_j-x_0} \cdots \frac{x-x_{j-1}}{x_j-x_{j-1}} \frac{x-x_{j+1}}{x_j-x_{j+1}} \cdots \frac{x-x_{n}}{x_j-x_{n}}\,\!$

l j(x) обладают следущими свойствами:

являются многочленами степени n
l j(x j) = 1
l j(x i) = 0 при $i\ne j$

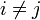
Отсюда следует, что L(x), как линейная комбинация l j(x), может иметь степень не больше n, и L(x j) = y j,

## Применения

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значения y j = f(x j) в некоторых точках. Тогда мы можем интерполировать эту функцию как

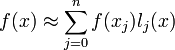
$f(x) \approx \sum_{j=0}^n f(x_j) l_j(x)$

В частности,

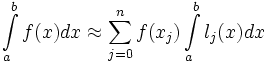
$\int\limits_a^b f(x)dx \approx \sum_{j=0}^n f(x_j) \int\limits_a^b l_j(x) dx$

Значения интегралов от l j не зависят от f(x), и их можно вычислить заранее, зная последовательность x i.

### Для случая равномерного распределения по отрезку узлов интерполяции

В указанном случае можно выразить x i через расстояние между узлами интерполяции h и начальную точку _x_0:

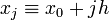$x_j \equiv {x_0 + jh}$ ,

и, следовательно,

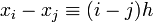${x_i - x_j} \equiv (i - j)h$ .

Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

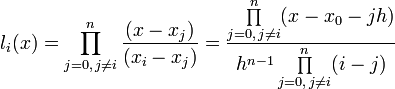
$l_i(x) = { \prod_{j=0,\,j \ne i}^n {(x - x_j) \over (x_i - x_j)}} =** **{\prod\limits_{j=0,\,j \ne i}^n (x - x_0 - jh) \over h^{n-1} \prod\limits_{j=0,\,j \ne i}^n (i - j)}$

Теперь можно ввести замену переменной

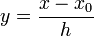
$y = {{x - x_0} \over h}\,\!$

и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования алгоритмов с многобайтным представлением чисел.

## Внешние ссылки

*** Аппроксимация функций.**

Wikimedia Foundation.2010.

### Полезное

Смотреть что такое "Многочлен Лагранжа" в других словарях:

Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для пар чисел , где все различны, существует единственный многочлен степени не более , для которого . В простейшем случае ( … Википедия
Лагранжа полином — Интерполяционный многочлен Лагранжа многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi.… … Википедия
Многочлен — Запрос «Полином» перенаправляется сюда; см. также другие значения. Многочлен (или полином) от n переменных это конечная формальная сумма вида , где есть набор из целых неотрицательных чисел (называется мультииндекс), число… … Википедия
Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
Многочлен Бернштейна — В вычислительной математике многочлены Бернштейна это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна. [1] [2] Устойчивым алгоритмом вычисления многочленов в форме Бернштейна является алгоритм… … Википедия
Многочлен Тейлора — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды… … Википедия
Интерполяционная формула Лагранжа — Интерполяционный многочлен Лагранжа многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi.… … Википедия
Полином Лагранжа — Интерполяционный многочлен Лагранжа многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi.… … Википедия
Список объектов, названных в честь Лагранжа — Существует несколько математических и физических объектов, носящих имя французского математика XVIII века Луи Жозефа Лагранжа: Теоремы Теорема Лагранжа в математическом анализе см. формула конечных приращений Теорема Лагранжа (теория групп) … Википедия
Интерполяционный многочлен — Интерполяционный многочлен: Интерполяционный многочлен Лагранжа Интерполяционный многочлен Ньютона Интерполяция алгебраическими многочленами … Википедия