Обыкновенные дифференциальные уравнения | это... Что такое Обыкновенные дифференциальные уравнения? (original) (raw)

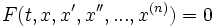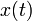Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида F(t,x,x',x'',...,x^{(n)})=0\!, где x(t)\! — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени 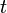t\!, штрих означает дифференцирование по 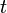t\!. Число 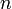n\! называется порядком дифференциального уравнения.

Решением дифференциального уравнения называется n раз дифференцируемая функция 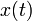x(t)\!, удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение.

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.

Содержание

Примеры

Дифференциальные уравнения первого порядка

Уравнения с разделяющимися переменными

Дифференциальное уравнение \dot{y} = f(x,y) называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде f(x,y) = _f_1(x)_f_2(y). Тогда, в случае f_2(y)\neq 0, общим решением уравнения является \int\!\frac{dy}{f_2(y)} = \int\! f_1(x)\,dx.

Примеры физических задач, приводящих к уравнениям с разделяющимися переменными

Охлаждение тела

Пусть T — температура тела, _T_0 — температура окружающей среды (T > _T_0). Пусть Q — количество теплоты, c — удельная теплоёмкость. Тогда количество теплоты передаваемое окружающей среде до выравнивания температур выражается формулой Q = m c(T − _T_0), или, в дифференциальной форме, dQ = mc\,dT. С другой стороны скорость отдачи тепла можно выразить в виде dQ = -k(T-T_0)\,dt, где k — некий коэффициент пропорциональности. Исключая из этих двух уравнений d Q получаем уравнение с разделяющимися переменными:

mc\,dT = -k(T-T_0)\,dt.

Общим решением этого уравнения является семейство функций T = T_0+C e^{-\frac{kt}{mc}}.

Однородные уравнения

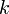Дифференциальное уравнение \dot{y} = f(x,y)\! называется однородным, если f(x, y)\! — однородная функция нулевой степени. Функция f(x, y)\! называется однородной степени k\!, если для любого \lambda > 0\! выполняется равенство f(\lambda x, \lambda y) = \lambda ^ k f(x,y)\!.

Замена y(x) = xz(x)\! приводит при x > 0\! однородное уравнение к уравнению с разделяющимися переменными:

f(x, xz) = x^{0} f(1, z) = f(1, z)\!

\dot{y} = x \dot{z} + z\!

Подставив в исходное уравнение, получаем:

\dot{z} = \frac{1}{x} (f(1, z) - z)\!,

что является уравнением с разделяющимися переменными.

Квазиоднородные уравнения

Дифференциальное уравнение \dot{y} = f(x,y)\! называется квазиоднородным, если для любого \lambda > 0\! выполняется соотношение f\left(\lambda ^ \alpha x, \lambda ^ \beta y\right) = \lambda ^ {\beta - \alpha} f(x, y)\!.

Данное уравнение решается заменой y = z ^ {\frac{\beta}{\alpha}}\!:

\dot{z} = \frac{\alpha}{\beta} \left(z ^ {- \frac{1}{\alpha}}\right) ^ {\beta - \alpha} f\left(x, z ^ \frac{\beta}{\alpha}\right)

В силу квазиоднородности, положив \lambda = z ^ {- \frac{1}{\alpha}}\!, получаем:

\left(z ^ {- \frac{1}{\alpha}}\right) ^ {\beta - \alpha} f \left(x, z ^ \frac{\beta}{\alpha}\right) = f\left(\frac{x}{z}, 1\right)

\dot{z} = \frac{\alpha}{\beta} f\left(\frac{x}{z}, 1\right),

что, очевидно, является однородным уравнением.

Линейные уравнения

Дифференциальное уравнение \dot{y} + a(x)y = b(x)\! называется линейным и может быть решено двумя методами: методом интегрирующего множителя или методом вариации постоянной.

Метод интегрирующего множителя

Пусть задана функция \mu(x)\! - интегрирующий множитель, в виде:

\mu(x) = e ^ {\int\! a(x)\,dx}\!

Умножим обе части исходного уравнения на \mu(x)\!, получим:

\dot{y}e ^ {\int\!a(x)\,dx} + ya(x) e ^ {\int\! a(x)\,dx} = b(x) \mu (x)\!

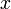Легко заметить, что левая часть является производной функции \mu(x) y(x)\! по x\!. Поэтому уравнение можно переписать:

(\mu (x) y(x))' = b(x) \mu (x)\!

Проинтегрируем:

y(x) \mu(x) = \int\!b(x) \mu (x)\,dx + C\!

Таким образом, решение линейного уравнения будет:

y(x) = e ^ {- \int\! a(x)\,dx}\left(\int\! b(x) \mu (x)\,dx + C\right)\!

Метод вариации постоянной (метод Лагранжа)

Рассмотрим однородное уравнение \dot{y} + a(x)y = 0\!. Очевидно, это уравнение с разделяющимися переменными, его решение:

y(x) = ce ^ {-\int\!a(x)\,dx}\!

Решения исходного уравнения будем искать в виде:

y(x) = c(x)e ^ {-\int\!a(x)\,dx}\!

Подставив полученное решение в исходное уравнение:

\dot{c} = b(x) e ^ {\int\!a(x)\,dx}\!,

получаем:

c(x) = c_1 + \int\!b(x) e ^ {\int\!a(x)\,dx}\,dx\!,

где _c_1 — произвольная константа.

Таким образом, решение исходного уравнения можно получить путем подстановки c(x)\! в решение однородного уравнения:

y(x) = e ^ {-\int\! a(x)\,dx}\left(c_1 + \int\! b(x)e ^ {\int\! a(x)\,dx}\,dx\right)

Уравнение Бернулли

Дифференциальное уравнение \dot{y} + a(x) y = b(x) y^n называется уравнением Бернулли, если n — действительное число, отличающееся от 0 и 1, так как при n = 0 и n = 1 уравнение обращается в линейное. Данное уравнение решается двумя способами:

Первый способ

Заменой

z = y ^ {1-n}\!.

уравнение приводится к линейному

\frac{1}{1-n} \dot{z} + a(x) z = b(x)

и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.

Второй способ

Заменим

y = u v.

Тогда

\dot{u}v + u(\dot{v} + a(x) v) = b(x) (uv)^n.

Подберем v(x) \not\equiv 0 так, чтобы было

\dot{v} + a(x) v = 0\!

для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка.
После этого для определения 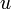u\! получаем уравнение \frac{\dot{u}}{u^n} = b(x)v^{n-1} — уравнение с разделяющимися переменными.

См. также

Литература

Wikimedia Foundation.2010.