Эффект Шубникова — де Гааза | это... Что такое Эффект Шубникова — де Гааза? (original) (raw)

Эффект Шубникова — де Гааза (или де Хааза) назван в честь советского физика Л. В. Шубникова и нидерландского физика В. де Хааза, открывших его в 1930 году. Наблюдаемый эффект заключался в осцилляциях магнетосопротивления плёнок висмута при низких температурах. Позже эффект Шубникова — де Гааза наблюдали в многих других металлах и полупроводниках. Эффект Шубникова — де Гааза используется для определения тензора эффективной массы и формы поверхности Ферми в металлах и полупроводниках.

Термины продольный и поперечный эффекты Шубникова — де Гааза вводят, чтобы различать ориентацию магнитного поля относительно направления течения электрического тока. Особый интерес заслуживает поперечный эффект Шубникова — де Гааза в двумерном электронном газе (ДЭГ).

Причина возникновения

Причина возникновения осцилляций проводимости и сопротивления кроется в особенностях энергетического спектра ДЭГ, а именно здесь речь идёт об уровнях Ландау с энергиями

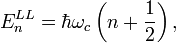
E^{LL}_n=\hbar\omega_c\left(n+\frac{1}{2}\right),

где 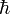\hbar — постоянная Планка, 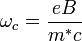\omega_c=\frac{eB}{m^*c} — циклотронная частота осциллятора Ландау, m * — эффективная масса электрона, n — номер уровня Ландау, c — скорость света,.

Плотность состояний ДЭГ 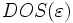DOS(\varepsilon) в квантующем магнитном поле для двумерного случая представляет собой набор дельтообразных особенностей

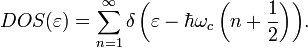
DOS(\varepsilon)=\sum_{n=1}^{\infty}{\delta\left(\varepsilon-\hbar\omega_c\left(n+\frac{1}{2}\right)\right)}.

Пусть уровень Ферми E F зафиксирован, например, уровнем Ферми в контактах. Тогда при возрастании магнитного поля B расстояние между уровнями Ландау начнёт увеличиваться, и они будут пересекать при условии 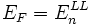E_F=E^{LL}_n уровень Ферми, и проводимость ДЭГ возрастет. Когда уровень Ферми находится между двумя уровнями Ландау, где нет электронов, дающих вклад в проводимость, наблюдается её минимум. Этот процесс повторяется при увеличении магнитного поля. Осцилляции магнетосопротивления периодичны по обратному магнитному полю и из их периода 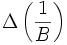\Delta\left(\frac{1}{B}\right) определяют концентрацию двумерного электронного газа (ДЭГ)

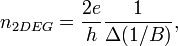
n_{2DEG}=\frac{2e}{h}\frac{1}{\Delta(1/B)},

где e — заряд электрона, h — постоянная Планка.

Осцилляции магнетосопротивления возникают и в другой постановке эксперимента, если зафиксировать магнитное поле и каким-либо образом менять концентрацию ДЭГ, например, в полевом транзисторе изменяя потенциал затвора.

Трёхмерный случай

Форма осцилляций слабо зависит от вида рассеивающего потенциала и следующее выражение, учитывающее уширение за счёт столкновений и температуры, а также спиновое расщепление, даёт хорошее приближение для описания поперечного эффекта Шубникова — де Гааза для трёхмерного электронного газа

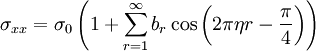
\sigma_{xx}=\sigma_0\left(1+\sum^{\infty}_{r=1}b_r\cos{\left(2\pi\eta r-\frac{\pi}{4}\right)}\right)

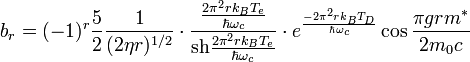
b_r=(-1)^r\frac{5}{2}\frac{1}{(2\eta r)^{1/2}}\cdot \frac{\frac{2\pi^2 rk_BT_e}{\hbar\omega_c}}{\mathrm{sh}{2\pi^2rk_BT_e \over \hbar\omega_c}} \cdot e^{-2\pi^2rk_BT_D \over \hbar\omega_c}\cos{\pi grm^{*}\over 2m_{0}c}

где 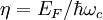\eta=E_F/\hbar\omega_c, T D — температура Дингля, определённая через столкновительному уширению Γ уровня как π_k_ B T D = Γ, k B — постоянная Больцмана, T e — температура электронного газа, g — множитель Ландэ для электрона (_g_-фактор), _m_0 — масса свободного электрона.

Аналогичное выражение для описания продольного эффекта Шубникова — де Гааза для трёхмерного электронного газа запишется в виде

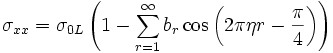
\sigma_{xx}=\sigma_{0L}\left(1-\sum^{\infty}_{r=1}b_r\cos{\left(2\pi\eta r-\frac{\pi}{4}\right)}\right)

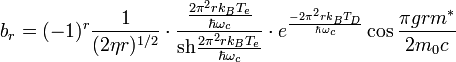
b_r=(-1)^r\frac{1}{(2\eta r)^{1/2}}\cdot\frac{\frac{2\pi^2rk_BT_e}{\hbar\omega_c}}{\mathrm{sh}{2\pi^2rk_BT_e \over \hbar\omega_c}}\cdot e^{-2\pi^2rk_BT_D \over \hbar\omega_c} \cos{\pi grm^{*} \over 2m_{0}c}

где 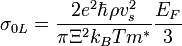\sigma_{0L}=\frac{2e^2\hbar\rho v_s^2}{\pi\Xi^2k_BTm^{*}}\frac{E_F}{3} (Ξ — деформационный потенциал).

Литература