Математика | это... Что такое Математика? (original) (raw)

Матема́тика (от др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов[1]. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов[2]. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы[3].

Содержание

Основные сведения

Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.

Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).

Этимология

Слово «математика» произошло от др.-греч. μάθημα (máthēma), что означает изучение, знание, наука, и др.-греч. μαθηματικός (mathēmatikós), первоначально означающего восприимчивый, успевающий[4], позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), на латыни ars mathematica, означает искусство математики.

В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год)[5]

Определения

Одно из первых определений предмета математики дал Декарт[6]:

К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.

В советское время классическим считалось определение из БСЭ[7], данное А. Н. Колмогоровым:

Математика… наука о количественных отношениях и пространственных формах действительного мира.

Это определение Энгельса[8]; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.

Формулировка Бурбаки[9]:

Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.

Приведём ещё несколько современных определений.

Современная теоретическая («чистая») математика — это наука о математических структурах, математических инвариантах различных систем и процессов[10].

Математика — наука, предоставляющая возможность исчисления моделей, приводимых к стандартному (каноническому) виду. Наука о нахождении решений аналитических моделей (анализ) средствами формальных преобразований[11].

Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:

Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.

«Математизирование» может остаться одним из проявлений творческой деятельности человека, подобно музицированию или литературному творчеству, ярким и самобытным, но прогнозирование его исторических судеб не поддаётся рационализации и не может быть объективным[12].

Разделы математики

1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:

и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.

Программа обучения по специальности математика[13] образована следующими учебными дисциплинами:

2. Математика как специальность научных работников Министерством образования и науки Российской Федерации[14] подразделяется на специальности:

3. Для систематизации научных работ используется раздел «Математика»[15] универсальной десятичной классификации (УДК).

4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.

Обозначения

Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.

Краткая история

Академиком А. Н. Колмогоровым предложена такая структура истории математики:

  1. Период зарождения математики, на протяжении которого был накоплен достаточно большой фактический материал;
  2. Период элементарной математики, начинающийся в VI—V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);
  3. Период математики переменных величин, охватывающий XVII—XVIII века, «который можно условно назвать также периодом „высшей математики“»;
  4. Период современной математики — математики XIX—XX века, в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».

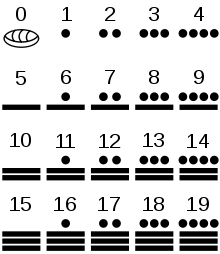
Цифры майя

Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.

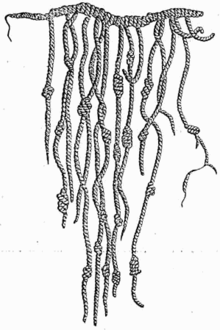
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.

Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.

Философия математики

Цели и методы

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «_Пространство \R^n, при n>3 является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях_».[16]

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Основания

Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.

Помимо скептического, известны нижеперечисленные подходы к данному вопросу.

Теоретико-множественный подход

Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.

Логицизм

Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.

Формализм

Данный подход предполагает изучение формальных систем на основе классической логики.

Интуиционизм

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).

Конструктивная математика

Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения[_прояснить_]. Согласно критерию конструктивности — «_существовать — значит быть построенным_».[17] Критерий конструктивности — более сильное требование, чем критерий непротиворечивости.[18]

Основные темы

Числа

Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

Числа — Натуральные числа — Целые числа — Рациональные числа — Вещественные числа — Комплексные числа — Гиперкомплексные числа — Кватернионы — Октонионы — Седенионы — Гиперреальные числа — Сюрреальные числа — p-адические числа — Математические постоянные — Названия чисел — Бесконечность — Базы

Просмотр этого шаблона Числовые системы
Счётныемножества Натуральные числа (\scriptstyle\mathbb{N}) • Целые (\scriptstyle\mathbb{Z}) • Рациональные (\scriptstyle\mathbb{Q}) • Алгебраические (\scriptstyle\overline{\mathbb{Q}}) • Периоды • Вычислимые • Арифметические
Вещественные числаи их расширения Вещественные (\scriptstyle\mathbb{R}) • Комплексные (\scriptstyle\mathbb{C}) • Кватернионы (\scriptstyle\mathbb{H}) • Числа Кэли (октавы, октонионы) (\scriptstyle\mathbb{O}) • Седенионы (\scriptstyle\mathbb{S}) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.)
Другиечисловые системы Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа
См. также Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион

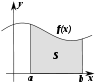
Преобразования

36 \div 9 = 4 Integral as region under curve.svg Vector field.svg \int 1_S\,d\mu=\mu(S)
Арифметика Дифференциальное и интегральное исчисление Векторный анализ Анализ
\frac{d^2}{dx^2} y = \frac{d}{dx} y + c Limitcycle.svg LorenzAttractor.png
Дифференциальные уравнения Динамические системы Теория хаоса

Арифметика — Векторный анализ — Анализ — Теория меры — Дифференциальные уравнения — Динамические системы — Теория хаоса — Перечень функций

Структуры

Теория множеств — Абстрактная алгебра — Теория групп — Алгебраические структуры — Алгебраическая геометрия — Теория чисел — Топология — Линейная алгебра — Универсальная алгебра — Теория категорий — Теория последовательностей

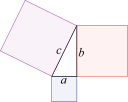
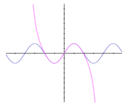
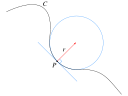
Пространственные отношения

Более наглядные подходы в математике.

Pythagorean.svg Taylorsine.gif Osculating circle.svg
Геометрия Тригонометрия Дифференциальная геометрия
Torus.jpg Koch curve.svg
Топология Фракталы

Геометрия — Тригонометрия — Алгебраическая геометрия — Топология — Дифференциальная геометрия — Дифференциальная топология — Алгебраическая топология — Линейная алгебра — Фракталы

Дискретная математика

Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.

Комбинаторика — Теория множеств — Теория решёток — Математическая логика — Теория вычислимости— Криптография — Теория функциональных систем — Теория графов — Теория алгоритмов — Логические исчисления — Информатика

Коды в системах классификации знаний

Онлайновые сервисы

Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные.[20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.

См. также

Популяризаторы науки

Примечания

  1. ↑ Энциклопедия Britannica
  2. ↑ Webster’s Online Dictionary
  3. ↑ Глава 2. Математика как язык науки. Сибирский открытый университет. Архивировано из первоисточника 2 февраля 2012. Проверено 5 октября 2010.
  4. ↑ Большой древнегреческий словарь (αω)
  5. ↑ Словарь русского языка XI—XVII вв. Выпуск 9 / Гл. ред. Ф. П. Филин. — М.: Наука, 1982. — С. 41.
  6. ↑ Декарт Р. Правила для руководства ума. М.-Л.: Соцэкгиз, 1936.
  7. ↑ См.: Математика БСЭ
  8. ↑ Маркс К., Энгельс Ф. Сочинения. 2-е изд. Т. 20. С. 37.
  9. ↑ Бурбаки Н. Архитектура математики. Очерки по истории математики / Перевод И. Г. Башмаковой под ред. К. А. Рыбникова. М.: ИЛ, 1963. С. 32, 258.
  10. ↑ Казиев В. М. Введение в математику
  11. ↑ Мухин О. И. Моделирование систем Учебное пособие. Пермь: РЦИ ПГТУ.
  12. ↑ Герман Вейль // Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 16.
  13. ↑ Государственный образовательный стандарт высшего профессионального образования. Специальность 01.01.00. «Математика». Квалификация — Математик. Москва, 2000 (Составлено под руководством О. Б. Лупанова)
  14. ↑ Номенклатура специальностей научных работников, утверждённая приказом Минобрнауки России от 25.02.2009 № 59
  15. ↑ УДК 51 Математика
  16. ↑ Я. С. Бугров, С. М. Никольский. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1988. С. 44.
  17. ↑ Н. И. Кондаков. Логический словарь-справочник. М.: Наука, 1975. С. 259.
  18. ↑ Г. И. Рузавин. О природе математического знания. М.: 1968.
  19. ↑ http://www.gsnti-norms.ru/norms/common/doc.asp?0&/norms/grnti/gr27.htm
  20. ↑ Например: http://mathworld.wolfram.com

Литература

Энциклопедии

Справочники

Книги

Занимательная математика

Ссылки

П: Портал «Математика»
wikt: Математика в Викисловаре?
q: Математика в Викицитатнике?
s: Математика в Викитеке?
commons: Математика на Викискладе?
n: Математика в Викиновостях?

Видеолекция

Образовательные сайты

Дискуссионные математические форумы

Судьба математической науки

Просмотр этого шаблона Наука
Научные направления Гуманитарные • Естественные • Общественные • Прикладные • Технические • Точные
Астрономия • Биология • География • Геология • Информатика • История • Лингвистика • Математика • Медицина • Психология • Политология • Социология • Физика • Филология • Химия • Экономика • Юриспруденция
Список академических дисциплин