Электрическая энергия | это... Что такое Электрическая энергия? (original) (raw)

Электромагнитная энергия — термин, под которым подразумевается энергия, заключенная в электромагнитном поле. Сюда же относятся частные случаи чистого электрического поля и чистого магнитного поля. Эта энергия равна механической работе, совершаемой при перемещении зарядов и проводников в электрическом и магнитном полях.

Содержание

1 Работа электрического поля по перемещению заряда
2 Мощность электрического тока в цепи
3 Энергия электрического и магнитного полей
4 Потоки энергии электромагнитного поля
5 См. также

Работа электрического поля по перемещению заряда

Понятие работы A электрического поля E по перемещению заряда Q вводится в полном соответствии с определением механической работы:

$A = \int F(x)\, dx = \int Q \cdot E(x)\, dx = Q \cdot U$

где $U = \int E\, dx$ — разность потенциалов (также употребляется термин напряжение)

Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t), в таком случае формула для работы следует переписать следующим образом:

$A = \int U(t)\, dQ = \int U(t) I(t)\, dt$

где $I(t) = {dQ \over dt}$ — сила тока

Мощность электрического тока в цепи

Мощность W электрического тока для участка цепи определяется обычным образом, как производная от работы A по времени, то есть выражением:

$W(t) = \frac{{dA}}{dt} = U(t) \cdot I(t)$

— это наиболее общее выражение для мощности в электрической цепи.

С учётом закона Ома : $U = I \cdot R$

Электрическую мощность, выделяемую на сопротивлении R можно выразить как через ток: $W = I(t)^2 \cdot R$ ,

так и через напряжение: $W = {{U(t)^2 } \over R}$

Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:

$A = \int W(t)\, dt = \int I(t)^2 \cdot R\, dt = \int {{U(t)^2 } \over R}\, dt$

Энергия электрического и магнитного полей

Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Следует отметить, что, строго говоря, термин энергия электромагнитного поля является не вполне корректным. Вычисление полной энергии электрического поля даже одного электрона приводит к значению равному бесконечности, поскольку соответствующий интеграл (см. ниже) расходится. Бесконечная энергия поля вполне конечного электрона составляет одну из теоретических проблем классической электродинамики. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определенной точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.

Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.

В системе СИ: $u = {\varepsilon _0 E^2 \over 2} + {\mu _0 H^2 \over {2}}$

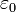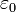где E — напряжённость электрического поля, H — напряжённость магнитного поля, $\varepsilon _0$ — электрическая постоянная, и $\! \mu_0$ — магнитная постоянная. Иногда для констант $\varepsilon _0$ и $\! \mu_0$ — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.

Потоки энергии электромагнитного поля

Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в российской научной традиции — вектор Умова-Пойнтинга).

В системе СИ вектор Пойнтинга равен: $\mathbf S = \mathbf E \times \mathbf H$ ,

— векторному произведению напряжённостей электрического и магнитного полей, и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.

Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей, и имеет совершенно тот же вид: $\mathbf S = \mathbf E \times \mathbf H$ .