Инъективное отображение | это... Что такое Инъективное отображение? (original) (raw)
Инъективное отображение
Инъективное отображение
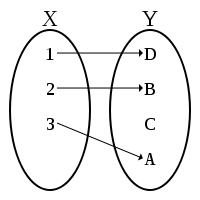
Инъективная функция.
Отображение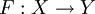 называется инъекцией (или вложением, или взаимно однозначным отображением в множество Y), если разные элементы множества X переводятся в разные элементы множества Y.
называется инъекцией (или вложением, или взаимно однозначным отображением в множество Y), если разные элементы множества X переводятся в разные элементы множества Y.
Формально это значит, что если два образа совпадают, то совпадают и прообразы (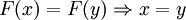 ). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть 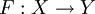 инъективно, если существует
инъективно, если существует 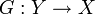 такое, что
такое, что 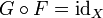 .
.
Примеры
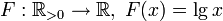 — инъективно.
— инъективно.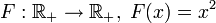 — инъективно.
— инъективно.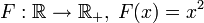 — не является инъективным (F( - 2) = F(2) = 4).
— не является инъективным (F( - 2) = F(2) = 4).
См. также
Литература
- Н. К. Верещагин, А.Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств.
- Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: «Лань», 2004—336 с.
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Инъективное отображение" в других словарях:
- ИНЪЕКЦИЯ — инъективное отображение, множества Ав множество В отображение f : при к ром различные элементы из Аимеют различные образы в В. И. наз. также взаимно однозначным отображением множества Ав множество В, или вложением. О. А. Иванова … Математическая энциклопедия
- Отношение эквивалентности — У этого термина существуют и другие значения, см. Эквивалентность. Отношение эквивалентности ( ) на множестве это бинарное отношение, для которого выполнены следующие условия: Рефлексивность: для любого в , Симметричность: если … Википедия
- Класс эквивалентности — Отношение эквивалентности ( ) на множестве X это бинарное отношение, для которого выполнены следующие условия: Рефлексивность: для любого a в X, Симметричность: если , то , Транзитивность: если … Википедия
- МНОЖЕСТВ КАТЕГОРИЯ — категория, объектами к рой являются всевозможные множества, морфиз мами всевозможные отображения множеств друг в друга, и умножение морфизмов определяется как последовательное выполнение отображений и Если теоретико категорные рассмотрения… … Математическая энциклопедия
- Хеширование — Хеш функция, отображающая множество имён в множество натуральныых чисел Хеширование (иногда «хэширование», англ. hashing) преобразование по детерменированному алгоритму входного массива данных прои … Википедия
- ШТЕЙНА ПРОСТРАНСТВО — голоморфно полное пространство, паракомпактноо комплексное аналитич. ространство обладающее следующими свойствами: 1) любое компактное аналитич. одмножество в Xконечно; 2) любой компакт допускает такую открытую окрестность Wв X, что множество… … Математическая энциклопедия