numpy.exp — NumPy v1.11 Manual (original) (raw)

numpy.exp(_x_[, _out_]) = <ufunc 'exp'>¶

Calculate the exponential of all elements in the input array.

Parameters:	x : array_like Input values.
Returns:	out : ndarray Output array, element-wise exponential of x.

See also

expm1

Calculate exp(x) - 1 for all elements in the array.

exp2

Calculate 2**x for all elements in the array.

Notes

The irrational number e is also known as Euler’s number. It is approximately 2.718281, and is the base of the natural logarithm,ln (this means that, if 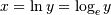$x = \ln y = \log_e y$ , then 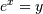$e^x = y$ . For real input, exp(x) is always positive.

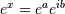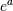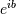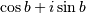For complex arguments, x = a + ib, we can write $e^x = e^a e^{ib}$ . The first term, $e^a$ , is already known (it is the real argument, described above). The second term, $e^{ib}$ , is $\cos b + i \sin b$ , a function with magnitude 1 and a periodic phase.

References

[R18]	Wikipedia, “Exponential function”,http://en.wikipedia.org/wiki/Exponential_function

[R19]	M. Abramovitz and I. A. Stegun, “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables,” Dover, 1964, p. 69,http://www.math.sfu.ca/~cbm/aands/page_69.htm

Examples

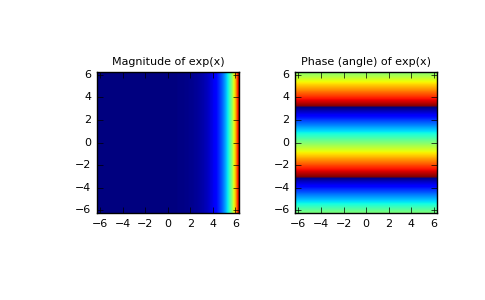
Plot the magnitude and phase of exp(x) in the complex plane:

import matplotlib.pyplot as plt

x = np.linspace(-2np.pi, 2np.pi, 100) xx = x + 1j * x[:, np.newaxis] # a + ib over complex plane out = np.exp(xx)

plt.subplot(121) plt.imshow(np.abs(out), ... extent=[-2np.pi, 2np.pi, -2np.pi, 2np.pi]) plt.title('Magnitude of exp(x)')

plt.subplot(122) plt.imshow(np.angle(out), ... extent=[-2np.pi, 2np.pi, -2np.pi, 2np.pi]) plt.title('Phase (angle) of exp(x)') plt.show()

(Source code, png, pdf)

../../_images/numpy-exp-1.png