numpy.random.geometric — NumPy v1.11 Manual (original) (raw)

numpy.random.geometric(p, size=None)¶

Draw samples from the geometric distribution.

Bernoulli trials are experiments with one of two outcomes: success or failure (an example of such an experiment is flipping a coin). The geometric distribution models the number of trials that must be run in order to achieve success. It is therefore supported on the positive integers, k = 1, 2, ....

The probability mass function of the geometric distribution is

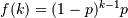
$f(k) = (1 - p)^{k - 1} p$

where p is the probability of success of an individual trial.

Parameters:	p : float The probability of success of an individual trial. size : int or tuple of ints, optional Output shape. If the given shape is, e.g., (m, n, k), thenm * n * k samples are drawn. Default is None, in which case a single value is returned.
Returns:	out : ndarray Samples from the geometric distribution, shaped according to_size_.

Examples

Draw ten thousand values from the geometric distribution, with the probability of an individual success equal to 0.35:

z = np.random.geometric(p=0.35, size=10000)

How many trials succeeded after a single run?

(z == 1).sum() / 10000. 0.34889999999999999 #random