numpy.random.logseries — NumPy v1.11 Manual (original) (raw)
numpy.random.logseries(p, size=None)¶
Draw samples from a logarithmic series distribution.
Samples are drawn from a log series distribution with specified shape parameter, 0 < p < 1.
| Parameters: | loc : float scale : float > 0. size : int or tuple of ints, optional Output shape. If the given shape is, e.g., (m, n, k), thenm * n * k samples are drawn. Default is None, in which case a single value is returned. |
|---|---|
| Returns: | samples : ndarray or scalar where the values are all integers in [0, n]. |
See also
scipy.stats.distributions.logser
probability density function, distribution or cumulative density function, etc.
Notes
The probability density for the Log Series distribution is
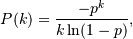
where p = probability.
The log series distribution is frequently used to represent species richness and occurrence, first proposed by Fisher, Corbet, and Williams in 1943 [2]. It may also be used to model the numbers of occupants seen in cars [3].
References
| [R237] | Buzas, Martin A.; Culver, Stephen J., Understanding regional species diversity through the log series distribution of occurrences: BIODIVERSITY RESEARCH Diversity & Distributions, Volume 5, Number 5, September 1999 , pp. 187-195(9). |
|---|
| [R238] | Fisher, R.A,, A.S. Corbet, and C.B. Williams. 1943. The relation between the number of species and the number of individuals in a random sample of an animal population. Journal of Animal Ecology, 12:42-58. |
|---|
| [R239] | D. J. Hand, F. Daly, D. Lunn, E. Ostrowski, A Handbook of Small Data Sets, CRC Press, 1994. |
|---|
| [R240] | Wikipedia, “Logarithmic-distribution”,http://en.wikipedia.org/wiki/Logarithmic-distribution |
|---|
Examples
Draw samples from the distribution:
a = .6 s = np.random.logseries(a, 10000) count, bins, ignored = plt.hist(s)
# plot against distribution
def logseries(k, p): ... return -p*k/(klog(1-p)) plt.plot(bins, logseries(bins, a)*count.max()/ logseries(bins, a).max(), 'r') plt.show()