numpy.random.poisson — NumPy v1.11 Manual (original) (raw)

numpy.random.poisson(lam=1.0, size=None)¶

Draw samples from a Poisson distribution.

The Poisson distribution is the limit of the binomial distribution for large N.

Parameters:	lam : float or sequence of float Expectation of interval, should be >= 0. A sequence of expectation intervals must be broadcastable over the requested size. size : int or tuple of ints, optional Output shape. If the given shape is, e.g., (m, n, k), thenm * n * k samples are drawn. Default is None, in which case a single value is returned.
Returns:	samples : ndarray or scalar The drawn samples, of shape size, if it was provided.

Notes

The Poisson distribution

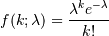
$f(k; \lambda)=\frac{\lambda^k e^{-\lambda}}{k!}$

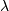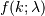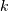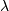For events with an expected separation $\lambda$ the Poisson distribution $f(k; \lambda)$ describes the probability of $k$ events occurring within the observed interval $\lambda$ .

Because the output is limited to the range of the C long type, a ValueError is raised when lam is within 10 sigma of the maximum representable value.

References

[R255]	Weisstein, Eric W. “Poisson Distribution.” From MathWorld–A Wolfram Web Resource.http://mathworld.wolfram.com/PoissonDistribution.html

[R256]	Wikipedia, “Poisson distribution”,http://en.wikipedia.org/wiki/Poisson_distribution

Examples

Draw samples from the distribution:

import numpy as np s = np.random.poisson(5, 10000)

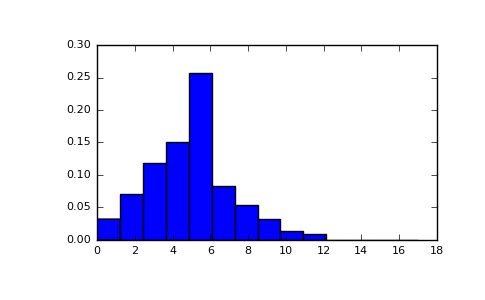
Display histogram of the sample:

import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s, 14, normed=True) plt.show()

(Source code, png, pdf)

../../_images/numpy-random-poisson-1_00_00.png

Draw each 100 values for lambda 100 and 500:

s = np.random.poisson(lam=(100., 500.), size=(100, 2))

()