SimpleRatioUniforms — SciPy v1.15.3 Manual (original) (raw)

scipy.stats.sampling.

class scipy.stats.sampling.SimpleRatioUniforms(dist, *, mode=None, pdf_area=1, domain=None, cdf_at_mode=None, random_state=None)#

Simple Ratio-of-Uniforms (SROU) Method.

SROU is based on the ratio-of-uniforms method that uses universal inequalities for constructing a (universal) bounding rectangle. It works for T-concave distributions with T(x) = -1/sqrt(x). The main advantage of the method is a fast setup. This can be beneficial if one repeatedly needs to generate small to moderate samples of a distribution with different shape parameters. In such a situation, the setup step ofNumericalInverseHermite or NumericalInversePolynomial will lead to poor performance.

Parameters:

distobject

An instance of a class with pdf method.

• pdf: PDF of the distribution. The signature of the PDF is expected to be: def pdf(self, x: float) -> float. i.e. the PDF should accept a Python float and return a Python float. It doesn’t need to integrate to 1 i.e. the PDF doesn’t need to be normalized. If not normalized, _pdf_area_should be set to the area under the PDF.

modefloat, optional

(Exact) Mode of the distribution. When the mode is None, a slow numerical routine is used to approximate it. Default is None.

pdf_areafloat, optional

Area under the PDF. Optionally, an upper bound to the area under the PDF can be passed at the cost of increased rejection constant. Default is 1.

domainlist or tuple of length 2, optional

The support of the distribution. Default is None. When None:

• If a support method is provided by the distribution object_dist_, it is used to set the domain of the distribution.
• Otherwise the support is assumed to be \((-\infty, \infty)\).

cdf_at_modefloat, optional

CDF at the mode. It can be given to increase the performance of the algorithm. The rejection constant is halfed when CDF at mode is given. Default is None.

random_state{None, int, numpy.random.Generator,

A NumPy random number generator or seed for the underlying NumPy random number generator used to generate the stream of uniform random numbers. If random_state is None (or np.random), the numpy.random.RandomStatesingleton is used. If random_state is an int, a new RandomState instance is used, seeded with random_state. If random_state is already a Generator or RandomState instance then that instance is used.

References

[2]

Leydold, Josef. “A simple universal generator for continuous and discrete univariate T-concave distributions.” ACM Transactions on Mathematical Software (TOMS) 27.1 (2001): 66-82

[3]

Leydold, Josef. “Short universal generators via generalized ratio-of-uniforms method.” Mathematics of Computation 72.243 (2003): 1453-1471

Examples

from scipy.stats.sampling import SimpleRatioUniforms import numpy as np

Suppose we have the normal distribution:

class StdNorm: ... def pdf(self, x): ... return np.exp(-0.5 * x**2)

Notice that the PDF doesn’t integrate to 1. We can either pass the exact area under the PDF during initialization of the generator or an upper bound to the exact area under the PDF. Also, it is recommended to pass the mode of the distribution to speed up the setup:

urng = np.random.default_rng() dist = StdNorm() rng = SimpleRatioUniforms(dist, mode=0, ... pdf_area=np.sqrt(2*np.pi), ... random_state=urng)

Now, we can use the rvs method to generate samples from the distribution:

If the CDF at mode is available, it can be set to improve the performance of rvs:

from scipy.stats import norm rng = SimpleRatioUniforms(dist, mode=0, ... pdf_area=np.sqrt(2*np.pi), ... cdf_at_mode=norm.cdf(0), ... random_state=urng) rvs = rng.rvs(1000)

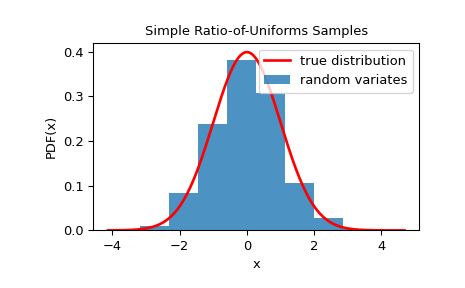
We can check that the samples are from the given distribution by visualizing its histogram:

import matplotlib.pyplot as plt x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000) fx = 1/np.sqrt(2*np.pi) * dist.pdf(x) fig, ax = plt.subplots() ax.plot(x, fx, 'r-', lw=2, label='true distribution') ax.hist(rvs, bins=10, density=True, alpha=0.8, label='random variates') ax.set_xlabel('x') ax.set_ylabel('PDF(x)') ax.set_title('Simple Ratio-of-Uniforms Samples') ax.legend() plt.show()

Methods