Центробежный и кулоновский барьеры (original) (raw)
Центробежный и кулоновский барьеры
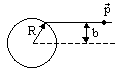 На ядро с радиусом R налетает частица с импульсом p и прицельным параметром b. Классический момент импульса налетающей (вылетающей) частицы pb равен величине ее орбитального момента
На ядро с радиусом R налетает частица с импульсом p и прицельным параметром b. Классический момент импульса налетающей (вылетающей) частицы pb равен величине ее орбитального момента
pb = ћ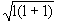 |
(с.1) |
|---|
Классическое условие "попадания" частицы в ядро b < R. Из соотношения (с.1), выразив импульс налетающей частицы через ее кинетическую энергию, и учитывая, что кинетическая энергия налетающей (вылетающей) должна быть больше высоты кулоновского барьера (T > Bц) получим
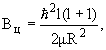 |
(c.2) |
|---|
где Bц - высота центробежного барьера, ћ - приведенная постоянная Планка, μ - приведенная масса частицы. Квантовая частица может попасть в ядро, проникнув сквозь барьер, и в случае, если кинетическая энергия частицы Т меньше высоты барьера, (T < Bц), однако, эффективность проникновения частицы в ядро в этом случае будет сильно подавлена из-за малой проницаемости барьера. Таким образом, при данной энергии Т эффективно принимают участие во взаимодействии частицы с орбитальными моментами l, удовлетворяющие условию
| l(l + 1) < 2μTR2/ћ2 | (с.3) |
|---|
Для заряженных частиц наряду с центробежным потенциальным барьером необходимо учитывать также кулоновский барьер. Высота кулоновского барьера на границе ядра
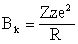 , , |
(с.4) |
|---|
где Z, z - атомные номера налетающей (вылетающей) частицы и ядра, R -радиус ядра, е - заряд электрона. Учитывая, что R = r0A1/3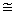 1.3 Фм и e2
1.3 Фм и e2 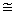 1.4 МэВ·Фм, можно переписать (с.4) в виде
1.4 МэВ·Фм, можно переписать (с.4) в виде
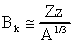 МэВ МэВ |
(с.4a) |
|---|
Для протонов за исключением самых легких ядер Bk> Bц (l = 1).