Ядерные реакции - сечение ядерной реакции (original) (raw)

Сечение ядерной реакции

Сечение ядерной реакции - величина характеризующая вероятность перехода системы двух взаимодействующих частиц в определенное конечное состояние.
Вероятность ядерного взаимодействия принято определять через эффективную площадь ядра 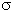, находящегося на пути пучка. Обозначим число частиц упавших на единичную площадь мишени, расположенную перпендикулярно оси пучка через N0. Пусть на этой площади находится n ядер. Тогда число взаимодействий определяется соотношением

где 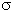называется полным сечением. Величина сечения может отличатся от геометрической площади сечения ядра на несколько порядков.
Количество ядер на единице площади можно рассчитать, если известна толщина мишени

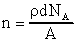,	(cr.2)

где ρ − плотность вещества мишени, d − толщина мишени, NA − число Авогадро, А − массовое число.
Сечения реакций с различными выходными каналами (например (p,n), (p,d) и.т.д.) называются парциальными сечениями. Часто в данной реакции выделяют сечения процессов приводящих к возбуждению различных состояний конечных ядер. Такие сечения также называют парциальными. Полное сечение реакций складывается из всех парциальных сечений реакций, возможных при данной энергии.

где 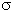b − парциальное сечение.
За единицу сечения принят 1 барн = 10-24см2.
В зависимости от поставленной задачи и условий эксперимента используют также понятия интегрального, дифференциального, дважды дифференциального и т.д. сечений.

_Интегральным сечением_реакции a + A →b + B называется величина

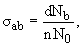	(cr.3)

где n − количество частиц мишени на единицу площади, N0 - количество попавших на мишень частиц a, dNb − количество частиц b, продуктов реакции.
**Дифференциальным сечением**реакции a + A →b + B называется величина

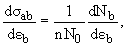	(cr.4)

где n − количество частиц мишени на единицу площади, N0 − количество попавших на мишень частиц a, dNb/dεb − количество частиц b, продуктов реакции, имеющих энергию в диапазоне
εb – εb+ dεb.
Дважды дифференциальным сечением реакции a + A →b + B называется величина

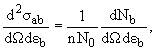	(cr.5)

где n − количество частиц мишени на единицу площади, N0 − количество попавших на мишень частиц a,
dNb/dΩdεb − количество частиц, продуктов данной реакции b, вылетевших в элемент телесного угла dΩ в направлении, характеризуемом полярным θ и азимутальным φ углами, и имеющих энергию в диапазоне εb – εb+ dεb.
Сечения связаны соотношениями:

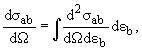	(cr.6)

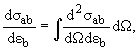	(cr.7)

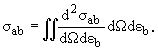	(cr.8)

Интегральные сечения σab реакции a + A→ b + B и обратной σba реакции b + B→ a + A связаны принципом детального равновесия:

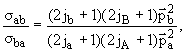	(cr.9)

где ja, jA, jb, jBспины , а aиbимпульсы частиц в системе центра инерции.
В случаях , когда в реакции участвует -квант необходимо учесть, что для него множитель 2j + 1 = 2, так как спин -кванта имеет 2 проекции.