Intro to Data Structures — pandas 0.24.0rc1 documentation (original) (raw)
We’ll start with a quick, non-comprehensive overview of the fundamental data structures in pandas to get you started. The fundamental behavior about data types, indexing, and axis labeling / alignment apply across all of the objects. To get started, import NumPy and load pandas into your namespace:
In [1]: import numpy as np
In [2]: import pandas as pd
Here is a basic tenet to keep in mind: data alignment is intrinsic. The link between labels and data will not be broken unless done so explicitly by you.
We’ll give a brief intro to the data structures, then consider all of the broad categories of functionality and methods in separate sections.
Series¶
Series is a one-dimensional labeled array capable of holding any data type (integers, strings, floating point numbers, Python objects, etc.). The axis labels are collectively referred to as the index. The basic method to create a Series is to call:
s = pd.Series(data, index=index)
Here, data can be many different things:
- a Python dict
- an ndarray
- a scalar value (like 5)
The passed index is a list of axis labels. Thus, this separates into a few cases depending on what data is:
From ndarray
If data is an ndarray, index must be the same length as data. If no index is passed, one will be created having values [0, ..., len(data) - 1].
In [3]: s = pd.Series(np.random.randn(5), index=['a', 'b', 'c', 'd', 'e'])
In [4]: s Out[4]: a 0.469112 b -0.282863 c -1.509059 d -1.135632 e 1.212112 dtype: float64
In [5]: s.index Out[5]: Index(['a', 'b', 'c', 'd', 'e'], dtype='object')
In [6]: pd.Series(np.random.randn(5)) Out[6]: 0 -0.173215 1 0.119209 2 -1.044236 3 -0.861849 4 -2.104569 dtype: float64
Note
pandas supports non-unique index values. If an operation that does not support duplicate index values is attempted, an exception will be raised at that time. The reason for being lazy is nearly all performance-based (there are many instances in computations, like parts of GroupBy, where the index is not used).
From dict
Series can be instantiated from dicts:
In [7]: d = {'b': 1, 'a': 0, 'c': 2}
In [8]: pd.Series(d) Out[8]: b 1 a 0 c 2 dtype: int64
Note
When the data is a dict, and an index is not passed, the Series index will be ordered by the dict’s insertion order, if you’re using Python version >= 3.6 and Pandas version >= 0.23.
If you’re using Python < 3.6 or Pandas < 0.23, and an index is not passed, the Series index will be the lexically ordered list of dict keys.
In the example above, if you were on a Python version lower than 3.6 or a Pandas version lower than 0.23, the Series would be ordered by the lexical order of the dict keys (i.e. ['a', 'b', 'c'] rather than ['b', 'a', 'c']).
If an index is passed, the values in data corresponding to the labels in the index will be pulled out.
In [9]: d = {'a': 0., 'b': 1., 'c': 2.}
In [10]: pd.Series(d) Out[10]: a 0.0 b 1.0 c 2.0 dtype: float64
In [11]: pd.Series(d, index=['b', 'c', 'd', 'a']) Out[11]: b 1.0 c 2.0 d NaN a 0.0 dtype: float64
Note
NaN (not a number) is the standard missing data marker used in pandas.
From scalar value
If data is a scalar value, an index must be provided. The value will be repeated to match the length of index.
In [12]: pd.Series(5., index=['a', 'b', 'c', 'd', 'e']) Out[12]: a 5.0 b 5.0 c 5.0 d 5.0 e 5.0 dtype: float64
Series is ndarray-like¶
Series acts very similarly to a ndarray, and is a valid argument to most NumPy functions. However, operations such as slicing will also slice the index.
In [13]: s[0] Out[13]: 0.46911229990718628
In [14]: s[:3] Out[14]: a 0.469112 b -0.282863 c -1.509059 dtype: float64
In [15]: s[s > s.median()] Out[15]: a 0.469112 e 1.212112 dtype: float64
In [16]: s[[4, 3, 1]] Out[16]: e 1.212112 d -1.135632 b -0.282863 dtype: float64
In [17]: np.exp(s) Out[17]: a 1.598575 b 0.753623 c 0.221118 d 0.321219 e 3.360575 dtype: float64
Note
We will address array-based indexing like s[[4, 3, 1]]in section.
Like a NumPy array, a pandas Series has a dtype.
In [18]: s.dtype Out[18]: dtype('float64')
This is often a NumPy dtype. However, pandas and 3rd-party libraries extend NumPy’s type system in a few places, in which case the dtype would be a ExtensionDtype. Some examples within pandas are Categorical Data and Nullable Integer Data Type. See dtypesfor more.
If you need the actual array backing a Series, use Series.array.
In [19]: s.array Out[19]: [ 0.46911229990718628, -0.28286334432866328, -1.5090585031735124, -1.1356323710171934, 1.2121120250208506] Length: 5, dtype: float64
Accessing the array can be useful when you need to do some operation without the index (to disable automatic alignment, for example).
Series.array will always be an ExtensionArray. Briefly, an ExtensionArray is a thin wrapper around one or more concrete arrays like anumpy.ndarray. Pandas knows how to take an ExtensionArray and store it in a Series or a column of a DataFrame. See dtypes for more.
While Series is ndarray-like, if you need an actual ndarray, then useSeries.to_numpy().
In [20]: s.to_numpy() Out[20]: array([ 0.4691, -0.2829, -1.5091, -1.1356, 1.2121])
Even if the Series is backed by a ExtensionArray,Series.to_numpy() will return a NumPy ndarray.
Series is dict-like¶
A Series is like a fixed-size dict in that you can get and set values by index label:
In [21]: s['a'] Out[21]: 0.46911229990718628
In [22]: s['e'] = 12.
In [23]: s Out[23]: a 0.469112 b -0.282863 c -1.509059 d -1.135632 e 12.000000 dtype: float64
In [24]: 'e' in s Out[24]: True
In [25]: 'f' in s Out[25]: False
If a label is not contained, an exception is raised:
Using the get method, a missing label will return None or specified default:
In [26]: s.get('f')
In [27]: s.get('f', np.nan) Out[27]: nan
See also the section on attribute access.
Vectorized operations and label alignment with Series¶
When working with raw NumPy arrays, looping through value-by-value is usually not necessary. The same is true when working with Series in pandas. Series can also be passed into most NumPy methods expecting an ndarray.
In [28]: s + s Out[28]: a 0.938225 b -0.565727 c -3.018117 d -2.271265 e 24.000000 dtype: float64
In [29]: s * 2 Out[29]: a 0.938225 b -0.565727 c -3.018117 d -2.271265 e 24.000000 dtype: float64
In [30]: np.exp(s) Out[30]: a 1.598575 b 0.753623 c 0.221118 d 0.321219 e 162754.791419 dtype: float64
A key difference between Series and ndarray is that operations between Series automatically align the data based on label. Thus, you can write computations without giving consideration to whether the Series involved have the same labels.
In [31]: s[1:] + s[:-1] Out[31]: a NaN b -0.565727 c -3.018117 d -2.271265 e NaN dtype: float64
The result of an operation between unaligned Series will have the union of the indexes involved. If a label is not found in one Series or the other, the result will be marked as missing NaN. Being able to write code without doing any explicit data alignment grants immense freedom and flexibility in interactive data analysis and research. The integrated data alignment features of the pandas data structures set pandas apart from the majority of related tools for working with labeled data.
Note
In general, we chose to make the default result of operations between differently indexed objects yield the union of the indexes in order to avoid loss of information. Having an index label, though the data is missing, is typically important information as part of a computation. You of course have the option of dropping labels with missing data via thedropna function.
Name attribute¶
Series can also have a name attribute:
In [32]: s = pd.Series(np.random.randn(5), name='something')
In [33]: s Out[33]: 0 -0.494929 1 1.071804 2 0.721555 3 -0.706771 4 -1.039575 Name: something, dtype: float64
In [34]: s.name Out[34]: 'something'
The Series name will be assigned automatically in many cases, in particular when taking 1D slices of DataFrame as you will see below.
New in version 0.18.0.
You can rename a Series with the pandas.Series.rename() method.
In [35]: s2 = s.rename("different")
In [36]: s2.name Out[36]: 'different'
Note that s and s2 refer to different objects.
DataFrame¶
DataFrame is a 2-dimensional labeled data structure with columns of potentially different types. You can think of it like a spreadsheet or SQL table, or a dict of Series objects. It is generally the most commonly used pandas object. Like Series, DataFrame accepts many different kinds of input:
- Dict of 1D ndarrays, lists, dicts, or Series
- 2-D numpy.ndarray
- Structured or record ndarray
- A
Series - Another
DataFrame
Along with the data, you can optionally pass index (row labels) andcolumns (column labels) arguments. If you pass an index and / or columns, you are guaranteeing the index and / or columns of the resulting DataFrame. Thus, a dict of Series plus a specific index will discard all data not matching up to the passed index.
If axis labels are not passed, they will be constructed from the input data based on common sense rules.
Note
When the data is a dict, and columns is not specified, the DataFramecolumns will be ordered by the dict’s insertion order, if you are using Python version >= 3.6 and Pandas >= 0.23.
If you are using Python < 3.6 or Pandas < 0.23, and columns is not specified, the DataFrame columns will be the lexically ordered list of dict keys.
From dict of Series or dicts¶
The resulting index will be the union of the indexes of the various Series. If there are any nested dicts, these will first be converted to Series. If no columns are passed, the columns will be the ordered list of dict keys.
In [37]: d = {'one': pd.Series([1., 2., 3.], index=['a', 'b', 'c']), ....: 'two': pd.Series([1., 2., 3., 4.], index=['a', 'b', 'c', 'd'])} ....:
In [38]: df = pd.DataFrame(d)
In [39]: df Out[39]: one two a 1.0 1.0 b 2.0 2.0 c 3.0 3.0 d NaN 4.0
In [40]: pd.DataFrame(d, index=['d', 'b', 'a']) Out[40]: one two d NaN 4.0 b 2.0 2.0 a 1.0 1.0
In [41]: pd.DataFrame(d, index=['d', 'b', 'a'], columns=['two', 'three']) Out[41]: two three d 4.0 NaN b 2.0 NaN a 1.0 NaN
The row and column labels can be accessed respectively by accessing theindex and columns attributes:
Note
When a particular set of columns is passed along with a dict of data, the passed columns override the keys in the dict.
In [42]: df.index Out[42]: Index(['a', 'b', 'c', 'd'], dtype='object')
In [43]: df.columns Out[43]: Index(['one', 'two'], dtype='object')
From dict of ndarrays / lists¶
The ndarrays must all be the same length. If an index is passed, it must clearly also be the same length as the arrays. If no index is passed, the result will be range(n), where n is the array length.
In [44]: d = {'one': [1., 2., 3., 4.], ....: 'two': [4., 3., 2., 1.]} ....:
In [45]: pd.DataFrame(d) Out[45]: one two 0 1.0 4.0 1 2.0 3.0 2 3.0 2.0 3 4.0 1.0
In [46]: pd.DataFrame(d, index=['a', 'b', 'c', 'd']) Out[46]: one two a 1.0 4.0 b 2.0 3.0 c 3.0 2.0 d 4.0 1.0
From structured or record array¶
This case is handled identically to a dict of arrays.
In [47]: data = np.zeros((2, ), dtype=[('A', 'i4'), ('B', 'f4'), ('C', 'a10')])
In [48]: data[:] = [(1, 2., 'Hello'), (2, 3., "World")]
In [49]: pd.DataFrame(data) Out[49]: A B C 0 1 2.0 b'Hello' 1 2 3.0 b'World'
In [50]: pd.DataFrame(data, index=['first', 'second']) Out[50]: A B C first 1 2.0 b'Hello' second 2 3.0 b'World'
In [51]: pd.DataFrame(data, columns=['C', 'A', 'B']) Out[51]: C A B 0 b'Hello' 1 2.0 1 b'World' 2 3.0
Note
DataFrame is not intended to work exactly like a 2-dimensional NumPy ndarray.
From a list of dicts¶
In [52]: data2 = [{'a': 1, 'b': 2}, {'a': 5, 'b': 10, 'c': 20}]
In [53]: pd.DataFrame(data2) Out[53]: a b c 0 1 2 NaN 1 5 10 20.0
In [54]: pd.DataFrame(data2, index=['first', 'second']) Out[54]: a b c first 1 2 NaN second 5 10 20.0
In [55]: pd.DataFrame(data2, columns=['a', 'b']) Out[55]: a b 0 1 2 1 5 10
From a dict of tuples¶
You can automatically create a MultiIndexed frame by passing a tuples dictionary.
In [56]: pd.DataFrame({('a', 'b'): {('A', 'B'): 1, ('A', 'C'): 2},
....: ('a', 'a'): {('A', 'C'): 3, ('A', 'B'): 4},
....: ('a', 'c'): {('A', 'B'): 5, ('A', 'C'): 6},
....: ('b', 'a'): {('A', 'C'): 7, ('A', 'B'): 8},
....: ('b', 'b'): {('A', 'D'): 9, ('A', 'B'): 10}})
....:
Out[56]:
a b
b a c a b
A B 1.0 4.0 5.0 8.0 10.0
C 2.0 3.0 6.0 7.0 NaN
D NaN NaN NaN NaN 9.0
From a Series¶
The result will be a DataFrame with the same index as the input Series, and with one column whose name is the original name of the Series (only if no other column name provided).
Missing Data
Much more will be said on this topic in the Missing datasection. To construct a DataFrame with missing data, we use np.nan to represent missing values. Alternatively, you may pass a numpy.MaskedArrayas the data argument to the DataFrame constructor, and its masked entries will be considered missing.
Alternate Constructors¶
DataFrame.from_dict
DataFrame.from_dict takes a dict of dicts or a dict of array-like sequences and returns a DataFrame. It operates like the DataFrame constructor except for the orient parameter which is 'columns' by default, but which can be set to 'index' in order to use the dict keys as row labels.
In [57]: pd.DataFrame.from_dict(dict([('A', [1, 2, 3]), ('B', [4, 5, 6])])) Out[57]: A B 0 1 4 1 2 5 2 3 6
If you pass orient='index', the keys will be the row labels. In this case, you can also pass the desired column names:
In [58]: pd.DataFrame.from_dict(dict([('A', [1, 2, 3]), ('B', [4, 5, 6])]), ....: orient='index', columns=['one', 'two', 'three']) ....: Out[58]: one two three A 1 2 3 B 4 5 6
DataFrame.from_records
DataFrame.from_records takes a list of tuples or an ndarray with structured dtype. It works analogously to the normal DataFrame constructor, except that the resulting DataFrame index may be a specific field of the structured dtype. For example:
In [59]: data Out[59]: array([(1, 2., b'Hello'), (2, 3., b'World')], dtype=[('A', '<i4'), ('B', '<f4'), ('C', 'S10')])
In [60]: pd.DataFrame.from_records(data, index='C')
Out[60]:
A B
C
b'Hello' 1 2.0
b'World' 2 3.0
Column selection, addition, deletion¶
You can treat a DataFrame semantically like a dict of like-indexed Series objects. Getting, setting, and deleting columns works with the same syntax as the analogous dict operations:
In [61]: df['one'] Out[61]: a 1.0 b 2.0 c 3.0 d NaN Name: one, dtype: float64
In [62]: df['three'] = df['one'] * df['two']
In [63]: df['flag'] = df['one'] > 2
In [64]: df Out[64]: one two three flag a 1.0 1.0 1.0 False b 2.0 2.0 4.0 False c 3.0 3.0 9.0 True d NaN 4.0 NaN False
Columns can be deleted or popped like with a dict:
In [65]: del df['two']
In [66]: three = df.pop('three')
In [67]: df Out[67]: one flag a 1.0 False b 2.0 False c 3.0 True d NaN False
When inserting a scalar value, it will naturally be propagated to fill the column:
In [68]: df['foo'] = 'bar'
In [69]: df Out[69]: one flag foo a 1.0 False bar b 2.0 False bar c 3.0 True bar d NaN False bar
When inserting a Series that does not have the same index as the DataFrame, it will be conformed to the DataFrame’s index:
In [70]: df['one_trunc'] = df['one'][:2]
In [71]: df Out[71]: one flag foo one_trunc a 1.0 False bar 1.0 b 2.0 False bar 2.0 c 3.0 True bar NaN d NaN False bar NaN
You can insert raw ndarrays but their length must match the length of the DataFrame’s index.
By default, columns get inserted at the end. The insert function is available to insert at a particular location in the columns:
In [72]: df.insert(1, 'bar', df['one'])
In [73]: df Out[73]: one bar flag foo one_trunc a 1.0 1.0 False bar 1.0 b 2.0 2.0 False bar 2.0 c 3.0 3.0 True bar NaN d NaN NaN False bar NaN
Assigning New Columns in Method Chains¶
Inspired by dplyr’s mutate verb, DataFrame has an assign()method that allows you to easily create new columns that are potentially derived from existing columns.
In [74]: iris = pd.read_csv('data/iris.data')
In [75]: iris.head() Out[75]: SepalLength SepalWidth PetalLength PetalWidth Name 0 5.1 3.5 1.4 0.2 Iris-setosa 1 4.9 3.0 1.4 0.2 Iris-setosa 2 4.7 3.2 1.3 0.2 Iris-setosa 3 4.6 3.1 1.5 0.2 Iris-setosa 4 5.0 3.6 1.4 0.2 Iris-setosa
In [76]: (iris.assign(sepal_ratio=iris['SepalWidth'] / iris['SepalLength']) ....: .head()) ....: Out[76]: SepalLength SepalWidth PetalLength PetalWidth Name sepal_ratio 0 5.1 3.5 1.4 0.2 Iris-setosa 0.686275 1 4.9 3.0 1.4 0.2 Iris-setosa 0.612245 2 4.7 3.2 1.3 0.2 Iris-setosa 0.680851 3 4.6 3.1 1.5 0.2 Iris-setosa 0.673913 4 5.0 3.6 1.4 0.2 Iris-setosa 0.720000
In the example above, we inserted a precomputed value. We can also pass in a function of one argument to be evaluated on the DataFrame being assigned to.
In [77]: iris.assign(sepal_ratio=lambda x: (x['SepalWidth'] / x['SepalLength'])).head() Out[77]: SepalLength SepalWidth PetalLength PetalWidth Name sepal_ratio 0 5.1 3.5 1.4 0.2 Iris-setosa 0.686275 1 4.9 3.0 1.4 0.2 Iris-setosa 0.612245 2 4.7 3.2 1.3 0.2 Iris-setosa 0.680851 3 4.6 3.1 1.5 0.2 Iris-setosa 0.673913 4 5.0 3.6 1.4 0.2 Iris-setosa 0.720000
assign always returns a copy of the data, leaving the original DataFrame untouched.
Passing a callable, as opposed to an actual value to be inserted, is useful when you don’t have a reference to the DataFrame at hand. This is common when using assign in a chain of operations. For example, we can limit the DataFrame to just those observations with a Sepal Length greater than 5, calculate the ratio, and plot:
In [78]: (iris.query('SepalLength > 5') ....: .assign(SepalRatio=lambda x: x.SepalWidth / x.SepalLength, ....: PetalRatio=lambda x: x.PetalWidth / x.PetalLength) ....: .plot(kind='scatter', x='SepalRatio', y='PetalRatio')) ....: Out[78]: <matplotlib.axes._subplots.AxesSubplot at 0x7faf7b96eb00>
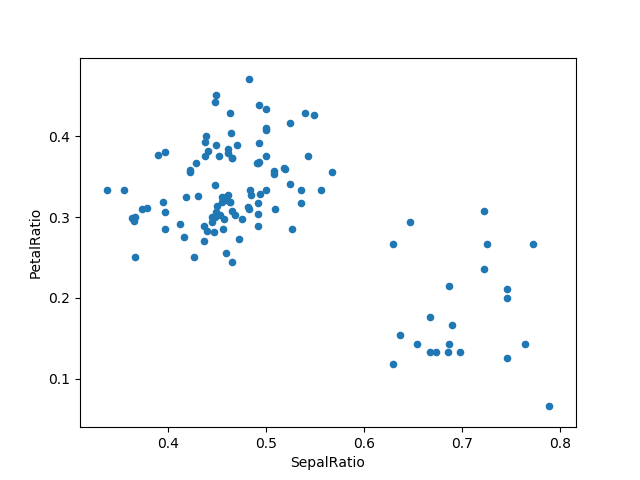
Since a function is passed in, the function is computed on the DataFrame being assigned to. Importantly, this is the DataFrame that’s been filtered to those rows with sepal length greater than 5. The filtering happens first, and then the ratio calculations. This is an example where we didn’t have a reference to the filtered DataFrame available.
The function signature for assign is simply **kwargs. The keys are the column names for the new fields, and the values are either a value to be inserted (for example, a Series or NumPy array), or a function of one argument to be called on the DataFrame. A copy of the original DataFrame is returned, with the new values inserted.
Changed in version 0.23.0.
Starting with Python 3.6 the order of **kwargs is preserved. This allows for dependent assignment, where an expression later in **kwargs can refer to a column created earlier in the same assign().
In [79]: dfa = pd.DataFrame({"A": [1, 2, 3], ....: "B": [4, 5, 6]}) ....:
In [80]: dfa.assign(C=lambda x: x['A'] + x['B'], ....: D=lambda x: x['A'] + x['C']) ....: Out[80]: A B C D 0 1 4 5 6 1 2 5 7 9 2 3 6 9 12
In the second expression, x['C'] will refer to the newly created column, that’s equal to dfa['A'] + dfa['B'].
To write code compatible with all versions of Python, split the assignment in two.
In [81]: dependent = pd.DataFrame({"A": [1, 1, 1]})
In [82]: (dependent.assign(A=lambda x: x['A'] + 1) ....: .assign(B=lambda x: x['A'] + 2)) ....: Out[82]: A B 0 2 4 1 2 4 2 2 4
Warning
Dependent assignment maybe subtly change the behavior of your code between Python 3.6 and older versions of Python.
If you wish write code that supports versions of python before and after 3.6, you’ll need to take care when passing assign expressions that
- Updating an existing column
- Referring to the newly updated column in the same
assign
For example, we’ll update column “A” and then refer to it when creating “B”.
dependent = pd.DataFrame({"A": [1, 1, 1]}) dependent.assign(A=lambda x: x["A"] + 1, B=lambda x: x["A"] + 2)
For Python 3.5 and earlier the expression creating B refers to the “old” value of A, [1, 1, 1]. The output is then
For Python 3.6 and later, the expression creating A refers to the “new” value of A, [2, 2, 2], which results in
Indexing / Selection¶
The basics of indexing are as follows:
| Operation | Syntax | Result |
|---|---|---|
| Select column | df[col] | Series |
| Select row by label | df.loc[label] | Series |
| Select row by integer location | df.iloc[loc] | Series |
| Slice rows | df[5:10] | DataFrame |
| Select rows by boolean vector | df[bool_vec] | DataFrame |
Row selection, for example, returns a Series whose index is the columns of the DataFrame:
In [83]: df.loc['b'] Out[83]: one 2 bar 2 flag False foo bar one_trunc 2 Name: b, dtype: object
In [84]: df.iloc[2] Out[84]: one 3 bar 3 flag True foo bar one_trunc NaN Name: c, dtype: object
For a more exhaustive treatment of sophisticated label-based indexing and slicing, see the section on indexing. We will address the fundamentals of reindexing / conforming to new sets of labels in thesection on reindexing.
Data alignment and arithmetic¶
Data alignment between DataFrame objects automatically align on both the columns and the index (row labels). Again, the resulting object will have the union of the column and row labels.
In [85]: df = pd.DataFrame(np.random.randn(10, 4), columns=['A', 'B', 'C', 'D'])
In [86]: df2 = pd.DataFrame(np.random.randn(7, 3), columns=['A', 'B', 'C'])
In [87]: df + df2 Out[87]: A B C D 0 0.045691 -0.014138 1.380871 NaN 1 -0.955398 -1.501007 0.037181 NaN 2 -0.662690 1.534833 -0.859691 NaN 3 -2.452949 1.237274 -0.133712 NaN 4 1.414490 1.951676 -2.320422 NaN 5 -0.494922 -1.649727 -1.084601 NaN 6 -1.047551 -0.748572 -0.805479 NaN 7 NaN NaN NaN NaN 8 NaN NaN NaN NaN 9 NaN NaN NaN NaN
When doing an operation between DataFrame and Series, the default behavior is to align the Series index on the DataFrame columns, thus broadcastingrow-wise. For example:
In [88]: df - df.iloc[0] Out[88]: A B C D 0 0.000000 0.000000 0.000000 0.000000 1 -1.359261 -0.248717 -0.453372 -1.754659 2 0.253128 0.829678 0.010026 -1.991234 3 -1.311128 0.054325 -1.724913 -1.620544 4 0.573025 1.500742 -0.676070 1.367331 5 -1.741248 0.781993 -1.241620 -2.053136 6 -1.240774 -0.869551 -0.153282 0.000430 7 -0.743894 0.411013 -0.929563 -0.282386 8 -1.194921 1.320690 0.238224 -1.482644 9 2.293786 1.856228 0.773289 -1.446531
In the special case of working with time series data, and the DataFrame index also contains dates, the broadcasting will be column-wise:
In [89]: index = pd.date_range('1/1/2000', periods=8)
In [90]: df = pd.DataFrame(np.random.randn(8, 3), index=index, columns=list('ABC'))
In [91]: df Out[91]: A B C 2000-01-01 -1.226825 0.769804 -1.281247 2000-01-02 -0.727707 -0.121306 -0.097883 2000-01-03 0.695775 0.341734 0.959726 2000-01-04 -1.110336 -0.619976 0.149748 2000-01-05 -0.732339 0.687738 0.176444 2000-01-06 0.403310 -0.154951 0.301624 2000-01-07 -2.179861 -1.369849 -0.954208 2000-01-08 1.462696 -1.743161 -0.826591
In [92]: type(df['A']) Out[92]: pandas.core.series.Series
In [93]: df - df['A'] Out[93]: 2000-01-01 00:00:00 2000-01-02 00:00:00 2000-01-03 00:00:00 2000-01-04 00:00:00 2000-01-05 00:00:00 ... 2000-01-07 00:00:00 2000-01-08 00:00:00 A B C 2000-01-01 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-02 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-03 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-04 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-05 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-06 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-07 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN 2000-01-08 NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN
[8 rows x 11 columns]
Warning
is now deprecated and will be removed in a future release. The preferred way to replicate this behavior is
For explicit control over the matching and broadcasting behavior, see the section on flexible binary operations.
Operations with scalars are just as you would expect:
In [94]: df * 5 + 2 Out[94]: A B C 2000-01-01 -4.134126 5.849018 -4.406237 2000-01-02 -1.638535 1.393469 1.510587 2000-01-03 5.478873 3.708672 6.798628 2000-01-04 -3.551681 -1.099880 2.748742 2000-01-05 -1.661697 5.438692 2.882222 2000-01-06 4.016548 1.225246 3.508122 2000-01-07 -8.899303 -4.849247 -2.771039 2000-01-08 9.313480 -6.715805 -2.132955
In [95]: 1 / df Out[95]: A B C 2000-01-01 -0.815112 1.299033 -0.780489 2000-01-02 -1.374179 -8.243600 -10.216313 2000-01-03 1.437247 2.926250 1.041965 2000-01-04 -0.900628 -1.612966 6.677871 2000-01-05 -1.365487 1.454041 5.667510 2000-01-06 2.479485 -6.453662 3.315381 2000-01-07 -0.458745 -0.730007 -1.047990 2000-01-08 0.683669 -0.573671 -1.209788
In [96]: df ** 4 Out[96]: A B C 2000-01-01 2.265327 0.351172 2.694833 2000-01-02 0.280431 0.000217 0.000092 2000-01-03 0.234355 0.013638 0.848376 2000-01-04 1.519910 0.147740 0.000503 2000-01-05 0.287640 0.223714 0.000969 2000-01-06 0.026458 0.000576 0.008277 2000-01-07 22.579530 3.521204 0.829033 2000-01-08 4.577374 9.233151 0.466834
Boolean operators work as well:
In [97]: df1 = pd.DataFrame({'a': [1, 0, 1], 'b': [0, 1, 1]}, dtype=bool)
In [98]: df2 = pd.DataFrame({'a': [0, 1, 1], 'b': [1, 1, 0]}, dtype=bool)
In [99]: df1 & df2 Out[99]: a b 0 False False 1 False True 2 True False
In [100]: df1 | df2 Out[100]: a b 0 True True 1 True True 2 True True
In [101]: df1 ^ df2 Out[101]: a b 0 True True 1 True False 2 False True
In [102]: -df1 Out[102]: a b 0 False True 1 True False 2 False False
Transposing¶
To transpose, access the T attribute (also the transpose function), similar to an ndarray:
only show the first 5 rows
In [103]: df[:5].T Out[103]: 2000-01-01 2000-01-02 2000-01-03 2000-01-04 2000-01-05 A -1.226825 -0.727707 0.695775 -1.110336 -0.732339 B 0.769804 -0.121306 0.341734 -0.619976 0.687738 C -1.281247 -0.097883 0.959726 0.149748 0.176444
DataFrame interoperability with NumPy functions¶
Elementwise NumPy ufuncs (log, exp, sqrt, …) and various other NumPy functions can be used with no issues on DataFrame, assuming the data within are numeric:
In [104]: np.exp(df) Out[104]: A B C 2000-01-01 0.293222 2.159342 0.277691 2000-01-02 0.483015 0.885763 0.906755 2000-01-03 2.005262 1.407386 2.610980 2000-01-04 0.329448 0.537957 1.161542 2000-01-05 0.480783 1.989212 1.192968 2000-01-06 1.496770 0.856457 1.352053 2000-01-07 0.113057 0.254145 0.385117 2000-01-08 4.317584 0.174966 0.437538
In [105]: np.asarray(df) Out[105]: array([[-1.2268, 0.7698, -1.2812], [-0.7277, -0.1213, -0.0979], [ 0.6958, 0.3417, 0.9597], [-1.1103, -0.62 , 0.1497], [-0.7323, 0.6877, 0.1764], [ 0.4033, -0.155 , 0.3016], [-2.1799, -1.3698, -0.9542], [ 1.4627, -1.7432, -0.8266]])
The dot method on DataFrame implements matrix multiplication:
In [106]: df.T.dot(df) Out[106]: A B C A 11.341858 -0.059772 3.007998 B -0.059772 6.520556 2.083308 C 3.007998 2.083308 4.310549
Similarly, the dot method on Series implements dot product:
In [107]: s1 = pd.Series(np.arange(5, 10))
In [108]: s1.dot(s1) Out[108]: 255
DataFrame is not intended to be a drop-in replacement for ndarray as its indexing semantics are quite different in places from a matrix.
Console display¶
Very large DataFrames will be truncated to display them in the console. You can also get a summary using info(). (Here I am reading a CSV version of the baseball dataset from the plyrR package):
In [109]: baseball = pd.read_csv('data/baseball.csv')
In [110]: print(baseball) id player year stint team lg g ab r h X2b X3b hr rbi sb cs bb so ibb hbp sh sf gidp 0 88641 womacto01 2006 2 CHN NL 19 50 6 14 1 0 1 2.0 1.0 1.0 4 4.0 0.0 0.0 3.0 0.0 0.0 1 88643 schilcu01 2006 1 BOS AL 31 2 0 1 0 0 0 0.0 0.0 0.0 0 1.0 0.0 0.0 0.0 0.0 0.0 .. ... ... ... ... ... .. .. ... .. ... ... ... .. ... ... ... .. ... ... ... ... ... ... 98 89533 aloumo01 2007 1 NYN NL 87 328 51 112 19 1 13 49.0 3.0 0.0 27 30.0 5.0 2.0 0.0 3.0 13.0 99 89534 alomasa02 2007 1 NYN NL 8 22 1 3 1 0 0 0.0 0.0 0.0 0 3.0 0.0 0.0 0.0 0.0 0.0
[100 rows x 23 columns]
In [111]: baseball.info() <class 'pandas.core.frame.DataFrame'> RangeIndex: 100 entries, 0 to 99 Data columns (total 23 columns): id 100 non-null int64 player 100 non-null object year 100 non-null int64 stint 100 non-null int64 team 100 non-null object lg 100 non-null object g 100 non-null int64 ab 100 non-null int64 r 100 non-null int64 h 100 non-null int64 X2b 100 non-null int64 X3b 100 non-null int64 hr 100 non-null int64 rbi 100 non-null float64 sb 100 non-null float64 cs 100 non-null float64 bb 100 non-null int64 so 100 non-null float64 ibb 100 non-null float64 hbp 100 non-null float64 sh 100 non-null float64 sf 100 non-null float64 gidp 100 non-null float64 dtypes: float64(9), int64(11), object(3) memory usage: 18.0+ KB
However, using to_string will return a string representation of the DataFrame in tabular form, though it won’t always fit the console width:
In [112]: print(baseball.iloc[-20:, :12].to_string()) id player year stint team lg g ab r h X2b X3b 80 89474 finlest01 2007 1 COL NL 43 94 9 17 3 0 81 89480 embreal01 2007 1 OAK AL 4 0 0 0 0 0 82 89481 edmonji01 2007 1 SLN NL 117 365 39 92 15 2 83 89482 easleda01 2007 1 NYN NL 76 193 24 54 6 0 84 89489 delgaca01 2007 1 NYN NL 139 538 71 139 30 0 85 89493 cormirh01 2007 1 CIN NL 6 0 0 0 0 0 86 89494 coninje01 2007 2 NYN NL 21 41 2 8 2 0 87 89495 coninje01 2007 1 CIN NL 80 215 23 57 11 1 88 89497 clemero02 2007 1 NYA AL 2 2 0 1 0 0 89 89498 claytro01 2007 2 BOS AL 8 6 1 0 0 0 90 89499 claytro01 2007 1 TOR AL 69 189 23 48 14 0 91 89501 cirilje01 2007 2 ARI NL 28 40 6 8 4 0 92 89502 cirilje01 2007 1 MIN AL 50 153 18 40 9 2 93 89521 bondsba01 2007 1 SFN NL 126 340 75 94 14 0 94 89523 biggicr01 2007 1 HOU NL 141 517 68 130 31 3 95 89525 benitar01 2007 2 FLO NL 34 0 0 0 0 0 96 89526 benitar01 2007 1 SFN NL 19 0 0 0 0 0 97 89530 ausmubr01 2007 1 HOU NL 117 349 38 82 16 3 98 89533 aloumo01 2007 1 NYN NL 87 328 51 112 19 1 99 89534 alomasa02 2007 1 NYN NL 8 22 1 3 1 0
Wide DataFrames will be printed across multiple rows by default:
In [113]: pd.DataFrame(np.random.randn(3, 12)) Out[113]: 0 1 2 3 4 5 6 7 8 9 10 11 0 -0.345352 1.314232 0.690579 0.995761 2.396780 0.014871 3.357427 -0.317441 -1.236269 0.896171 -0.487602 -0.082240 1 -2.182937 0.380396 0.084844 0.432390 1.519970 -0.493662 0.600178 0.274230 0.132885 -0.023688 2.410179 1.450520 2 0.206053 -0.251905 -2.213588 1.063327 1.266143 0.299368 -0.863838 0.408204 -1.048089 -0.025747 -0.988387 0.094055
You can change how much to print on a single row by setting the display.widthoption:
In [114]: pd.set_option('display.width', 40) # default is 80
In [115]: pd.DataFrame(np.random.randn(3, 12)) Out[115]: 0 1 2 3 4 5 6 7 8 9 10 11 0 1.262731 1.289997 0.082423 -0.055758 0.536580 -0.489682 0.369374 -0.034571 -2.484478 -0.281461 0.030711 0.109121 1 1.126203 -0.977349 1.474071 -0.064034 -1.282782 0.781836 -1.071357 0.441153 2.353925 0.583787 0.221471 -0.744471 2 0.758527 1.729689 -0.964980 -0.845696 -1.340896 1.846883 -1.328865 1.682706 -1.717693 0.888782 0.228440 0.901805
You can adjust the max width of the individual columns by setting display.max_colwidth
In [116]: datafile = {'filename': ['filename_01', 'filename_02'], .....: 'path': ["media/user_name/storage/folder_01/filename_01", .....: "media/user_name/storage/folder_02/filename_02"]} .....:
In [117]: pd.set_option('display.max_colwidth', 30)
In [118]: pd.DataFrame(datafile) Out[118]: filename path 0 filename_01 media/user_name/storage/fo... 1 filename_02 media/user_name/storage/fo...
In [119]: pd.set_option('display.max_colwidth', 100)
In [120]: pd.DataFrame(datafile) Out[120]: filename path 0 filename_01 media/user_name/storage/folder_01/filename_01 1 filename_02 media/user_name/storage/folder_02/filename_02
You can also disable this feature via the expand_frame_repr option. This will print the table in one block.
DataFrame column attribute access and IPython completion¶
If a DataFrame column label is a valid Python variable name, the column can be accessed like an attribute:
In [121]: df = pd.DataFrame({'foo1': np.random.randn(5), .....: 'foo2': np.random.randn(5)}) .....:
In [122]: df Out[122]: foo1 foo2 0 1.171216 -0.858447 1 0.520260 0.306996 2 -1.197071 -0.028665 3 -1.066969 0.384316 4 -0.303421 1.574159
In [123]: df.foo1 Out[123]: 0 1.171216 1 0.520260 2 -1.197071 3 -1.066969 4 -0.303421 Name: foo1, dtype: float64
The columns are also connected to the IPythoncompletion mechanism so they can be tab-completed:
In [5]: df.fo # noqa: E225, E999 df.foo1 df.foo2
Panel¶
Warning
In 0.20.0, Panel is deprecated and will be removed in a future version. See the section Deprecate Panel.
Panel is a somewhat less-used, but still important container for 3-dimensional data. The term panel data is derived from econometrics and is partially responsible for the name pandas: pan(el)-da(ta)-s. The names for the 3 axes are intended to give some semantic meaning to describing operations involving panel data and, in particular, econometric analysis of panel data. However, for the strict purposes of slicing and dicing a collection of DataFrame objects, you may find the axis names slightly arbitrary:
- items: axis 0, each item corresponds to a DataFrame contained inside
- major_axis: axis 1, it is the index (rows) of each of the DataFrames
- minor_axis: axis 2, it is the columns of each of the DataFrames
Construction of Panels works about like you would expect:
From 3D ndarray with optional axis labels¶
In [124]: wp = pd.Panel(np.random.randn(2, 5, 4), items=['Item1', 'Item2'], .....: major_axis=pd.date_range('1/1/2000', periods=5), .....: minor_axis=['A', 'B', 'C', 'D']) .....:
In [125]: wp Out[125]: <class 'pandas.core.panel.Panel'> Dimensions: 2 (items) x 5 (major_axis) x 4 (minor_axis) Items axis: Item1 to Item2 Major_axis axis: 2000-01-01 00:00:00 to 2000-01-05 00:00:00 Minor_axis axis: A to D
From dict of DataFrame objects¶
In [126]: data = {'Item1': pd.DataFrame(np.random.randn(4, 3)), .....: 'Item2': pd.DataFrame(np.random.randn(4, 2))} .....:
In [127]: pd.Panel(data) Out[127]: <class 'pandas.core.panel.Panel'> Dimensions: 2 (items) x 4 (major_axis) x 3 (minor_axis) Items axis: Item1 to Item2 Major_axis axis: 0 to 3 Minor_axis axis: 0 to 2
Note that the values in the dict need only be convertible to DataFrame. Thus, they can be any of the other valid inputs to DataFrame as per above.
One helpful factory method is Panel.from_dict, which takes a dictionary of DataFrames as above, and the following named parameters:
| Parameter | Default | Description |
|---|---|---|
| intersect | False | drops elements whose indices do not align |
| orient | items | use minor to use DataFrames’ columns as panel items |
For example, compare to the construction above:
In [128]: pd.Panel.from_dict(data, orient='minor') Out[128]: <class 'pandas.core.panel.Panel'> Dimensions: 3 (items) x 4 (major_axis) x 2 (minor_axis) Items axis: 0 to 2 Major_axis axis: 0 to 3 Minor_axis axis: Item1 to Item2
Orient is especially useful for mixed-type DataFrames. If you pass a dict of DataFrame objects with mixed-type columns, all of the data will get upcasted todtype=object unless you pass orient='minor':
In [129]: df = pd.DataFrame({'a': ['foo', 'bar', 'baz'], .....: 'b': np.random.randn(3)}) .....:
In [130]: df Out[130]: a b 0 foo -0.308853 1 bar -0.681087 2 baz 0.377953
In [131]: data = {'item1': df, 'item2': df}
In [132]: panel = pd.Panel.from_dict(data, orient='minor')
In [133]: panel['a'] Out[133]: item1 item2 0 foo foo 1 bar bar 2 baz baz
In [134]: panel['b'] Out[134]: item1 item2 0 -0.308853 -0.308853 1 -0.681087 -0.681087 2 0.377953 0.377953
In [135]: panel['b'].dtypes Out[135]: item1 float64 item2 float64 dtype: object
Note
Panel, being less commonly used than Series and DataFrame, has been slightly neglected feature-wise. A number of methods and options available in DataFrame are not available in Panel.
From DataFrame using to_panel method¶
to_panel converts a DataFrame with a two-level index to a Panel.
In [136]: midx = pd.MultiIndex(levels=[['one', 'two'], ['x', 'y']], .....: codes=[[1, 1, 0, 0], [1, 0, 1, 0]]) .....:
In [137]: df = pd.DataFrame({'A': [1, 2, 3, 4], 'B': [5, 6, 7, 8]}, index=midx)
In [138]: df.to_panel() Out[138]: <class 'pandas.core.panel.Panel'> Dimensions: 2 (items) x 2 (major_axis) x 2 (minor_axis) Items axis: A to B Major_axis axis: one to two Minor_axis axis: x to y
Item selection / addition / deletion¶
Similar to DataFrame functioning as a dict of Series, Panel is like a dict of DataFrames:
In [139]: wp['Item1'] Out[139]: A B C D 2000-01-01 1.588931 0.476720 0.473424 -0.242861 2000-01-02 -0.014805 -0.284319 0.650776 -1.461665 2000-01-03 -1.137707 -0.891060 -0.693921 1.613616 2000-01-04 0.464000 0.227371 -0.496922 0.306389 2000-01-05 -2.290613 -1.134623 -1.561819 -0.260838
In [140]: wp['Item3'] = wp['Item1'] / wp['Item2']
The API for insertion and deletion is the same as for DataFrame. And as with DataFrame, if the item is a valid Python identifier, you can access it as an attribute and tab-complete it in IPython.
Transposing¶
A Panel can be rearranged using its transpose method (which does not make a copy by default unless the data are heterogeneous):
In [141]: wp.transpose(2, 0, 1) Out[141]: <class 'pandas.core.panel.Panel'> Dimensions: 4 (items) x 3 (major_axis) x 5 (minor_axis) Items axis: A to D Major_axis axis: Item1 to Item3 Minor_axis axis: 2000-01-01 00:00:00 to 2000-01-05 00:00:00
Indexing / Selection¶
| Operation | Syntax | Result |
|---|---|---|
| Select item | wp[item] | DataFrame |
| Get slice at major_axis label | wp.major_xs(val) | DataFrame |
| Get slice at minor_axis label | wp.minor_xs(val) | DataFrame |
For example, using the earlier example data, we could do:
In [142]: wp['Item1'] Out[142]: A B C D 2000-01-01 1.588931 0.476720 0.473424 -0.242861 2000-01-02 -0.014805 -0.284319 0.650776 -1.461665 2000-01-03 -1.137707 -0.891060 -0.693921 1.613616 2000-01-04 0.464000 0.227371 -0.496922 0.306389 2000-01-05 -2.290613 -1.134623 -1.561819 -0.260838
In [143]: wp.major_xs(wp.major_axis[2]) Out[143]: Item1 Item2 Item3 A -1.137707 0.800193 -1.421791 B -0.891060 0.782098 -1.139320 C -0.693921 -1.069094 0.649074 D 1.613616 -1.099248 -1.467927
In [144]: wp.minor_axis Out[144]: Index(['A', 'B', 'C', 'D'], dtype='object')
In [145]: wp.minor_xs('C') Out[145]: Item1 Item2 Item3 2000-01-01 0.473424 -0.902937 -0.524316 2000-01-02 0.650776 -1.144073 -0.568824 2000-01-03 -0.693921 -1.069094 0.649074 2000-01-04 -0.496922 0.661084 -0.751678 2000-01-05 -1.561819 -1.056652 1.478083
Squeezing¶
Another way to change the dimensionality of an object is to squeeze a 1-len object, similar to wp['Item1'].
In [146]: wp.reindex(items=['Item1']).squeeze() Out[146]: A B C D 2000-01-01 1.588931 0.476720 0.473424 -0.242861 2000-01-02 -0.014805 -0.284319 0.650776 -1.461665 2000-01-03 -1.137707 -0.891060 -0.693921 1.613616 2000-01-04 0.464000 0.227371 -0.496922 0.306389 2000-01-05 -2.290613 -1.134623 -1.561819 -0.260838
In [147]: wp.reindex(items=['Item1'], minor=['B']).squeeze() Out[147]: 2000-01-01 0.476720 2000-01-02 -0.284319 2000-01-03 -0.891060 2000-01-04 0.227371 2000-01-05 -1.134623 Freq: D, Name: B, dtype: float64
Conversion to DataFrame¶
A Panel can be represented in 2D form as a hierarchically indexed DataFrame. See the section hierarchical indexingfor more on this. To convert a Panel to a DataFrame, use the to_framemethod:
In [148]: panel = pd.Panel(np.random.randn(3, 5, 4), items=['one', 'two', 'three'], .....: major_axis=pd.date_range('1/1/2000', periods=5), .....: minor_axis=['a', 'b', 'c', 'd']) .....:
In [149]: panel.to_frame()
Out[149]:
one two three
major minor
2000-01-01 a 0.493672 1.219492 -1.290493
b -2.461467 0.062297 0.787872
c -1.553902 -0.110388 1.515707
d 2.015523 -1.184357 -0.276487
2000-01-02 a -1.833722 -0.558081 -0.223762
b 1.771740 0.077849 1.397431
c -0.670027 0.629498 1.503874
d 0.049307 -1.035260 -0.478905
2000-01-03 a -0.521493 -0.438229 -0.135950
b -3.201750 0.503703 -0.730327
c 0.792716 0.413086 -0.033277
d 0.146111 -1.139050 0.281151
2000-01-04 a 1.903247 0.660342 -1.298915
b -0.747169 0.464794 -2.819487
c -0.309038 -0.309337 -0.851985
d 0.393876 -0.649593 -1.106952
2000-01-05 a 1.861468 0.683758 -0.937731
b 0.936527 -0.643834 -1.537770
c 1.255746 0.421287 0.555759
d -2.655452 1.032814 -2.277282
Deprecate Panel¶
Over the last few years, pandas has increased in both breadth and depth, with new features, datatype support, and manipulation routines. As a result, supporting efficient indexing and functional routines for Series, DataFrame and Panel has contributed to an increasingly fragmented and difficult-to-understand code base.
The 3-D structure of a Panel is much less common for many types of data analysis, than the 1-D of the Series or the 2-D of the DataFrame. Going forward it makes sense for pandas to focus on these areas exclusively.
Oftentimes, one can simply use a MultiIndex DataFrame for easily working with higher dimensional data.
In addition, the xarray package was built from the ground up, specifically in order to support the multi-dimensional analysis that is one of Panel s main use cases.Here is a link to the xarray panel-transition documentation.
In [150]: import pandas.util.testing as tm
In [151]: p = tm.makePanel()
In [152]: p Out[152]: <class 'pandas.core.panel.Panel'> Dimensions: 3 (items) x 30 (major_axis) x 4 (minor_axis) Items axis: ItemA to ItemC Major_axis axis: 2000-01-03 00:00:00 to 2000-02-11 00:00:00 Minor_axis axis: A to D
Convert to a MultiIndex DataFrame.
In [153]: p.to_frame()
Out[153]:
ItemA ItemB ItemC
major minor
2000-01-03 A -0.390201 -1.624062 -0.605044
B 1.562443 0.483103 0.583129
C -1.085663 0.768159 -0.273458
D 0.136235 -0.021763 -0.700648
2000-01-04 A 1.207122 -0.758514 0.878404
B 0.763264 0.061495 -0.876690
C -1.114738 0.225441 -0.335117
D 0.886313 -0.047152 -1.166607
2000-01-05 A 0.178690 -0.560859 -0.921485
B 0.162027 0.240767 -1.919354
C -0.058216 0.543294 -0.476268
D -1.350722 0.088472 -0.367236
2000-01-06 A -1.004168 -0.589005 -0.200312
B -0.902704 0.782413 -0.572707
C -0.486768 0.771931 -1.765602
D -0.886348 -0.857435 1.296674
2000-01-07 A -1.377627 -1.070678 0.522423
B 1.106010 0.628462 -1.736484
C 1.685148 -0.968145 0.578223
D -1.013316 -2.503786 0.641385
2000-01-10 A 0.499281 -1.681101 0.722511
B -0.199234 -0.880627 -1.335113
C 0.112572 -1.176383 0.242697
D 1.920906 -1.058041 -0.779432
2000-01-11 A -1.405256 0.403776 -1.702486
B 0.458265 0.777575 -1.244471
C -1.495309 -3.192716 0.208129
D -0.388231 -0.657981 0.602456
2000-01-12 A 0.162565 0.609862 -0.709535
B 0.491048 -0.779367 0.347339
... ... ... ...
2000-02-02 C -0.303961 -0.463752 -0.288962
D 0.104050 1.116086 0.506445
2000-02-03 A -2.338595 -0.581967 -0.801820
B -0.557697 -0.033731 -0.176382
C 0.625555 -0.055289 0.875359
D 0.174068 -0.443915 1.626369
2000-02-04 A -0.374279 -1.233862 -0.915751
B 0.381353 -1.108761 -1.970108
C -0.059268 -0.360853 -0.614618
D -0.439461 -0.200491 0.429518
2000-02-07 A -2.359958 -3.520876 -0.288156
B 1.337122 -0.314399 -1.044208
C 0.249698 0.728197 0.565375
D -0.741343 1.092633 0.013910
2000-02-08 A -1.157886 0.516870 -1.199945
B -1.531095 -0.860626 -0.821179
C 1.103949 1.326768 0.068184
D -0.079673 -1.675194 -0.458272
2000-02-09 A -0.551865 0.343125 -0.072869
B 1.331458 0.370397 -1.914267
C -1.087532 0.208927 0.788871
D -0.922875 0.437234 -1.531004
2000-02-10 A 1.592673 2.137827 -1.828740
B -0.571329 -1.761442 -0.826439
C 1.998044 0.292058 -0.280343
D 0.303638 0.388254 -0.500569
2000-02-11 A 1.559318 0.452429 -1.716981
B -0.026671 -0.899454 0.124808
C -0.244548 -2.019610 0.931536
D -0.917368 0.479630 0.870690
[120 rows x 3 columns]
Alternatively, one can convert to an xarray DataArray.
In [154]: p.to_xarray() Out[154]: <xarray.DataArray (items: 3, major_axis: 30, minor_axis: 4)> array([[[-0.390201, 1.562443, -1.085663, 0.136235], [ 1.207122, 0.763264, -1.114738, 0.886313], ..., [ 1.592673, -0.571329, 1.998044, 0.303638], [ 1.559318, -0.026671, -0.244548, -0.917368]],
[[-1.624062, 0.483103, 0.768159, -0.021763],
[-0.758514, 0.061495, 0.225441, -0.047152],
...,
[ 2.137827, -1.761442, 0.292058, 0.388254],
[ 0.452429, -0.899454, -2.01961 , 0.47963 ]],
[[-0.605044, 0.583129, -0.273458, -0.700648],
[ 0.878404, -0.87669 , -0.335117, -1.166607],
...,
[-1.82874 , -0.826439, -0.280343, -0.500569],
[-1.716981, 0.124808, 0.931536, 0.87069 ]]])Coordinates:
- items (items) object 'ItemA' 'ItemB' 'ItemC'
- major_axis (major_axis) datetime64[ns] 2000-01-03 2000-01-04 ... 2000-02-11
- minor_axis (minor_axis) object 'A' 'B' 'C' 'D'
You can see the full-documentation for the xarray package.