Acceleration of Gravity and Newton's Second Law (original) (raw)
Acceleration of Gravity is one of the most used physical constants - known from
Newton's Second Law
"Change of motion is proportional to the force applied, and take place along the straight line the force acts."
Newton's second law for the gravity force - weight - can be expressed as
W = Fg
= m ag
= m g (1)
where
W = F g = weight, gravity force (N, lbf)
m = mass (kg, slugs)
ag = g = acceleration of gravity (9.81 m/s2, 32.17405 ft/s2)
The force caused by gravity - ag - is called weight.
Note!
- mass is a property - a quantity with magnitude
- force is a vector - a quantity with magnitude and direction
The acceleration of gravity can be observed by measuring the change of velocity related to change of time for a free falling object:
ag = dv / dt (2)
where
dv = change in velocity (m/s, ft/s)
dt = change in time (s)
An object dropped in free air accelerates to speed 9.81 m/s (32.174 ft/s) in one - 1 - second .
- a heavy and a light body near the earth will fall to the earth with the same acceleration (when neglecting the air resistance)
Acceleration of Gravity in SI Units
1 ag = 1 g = 9.81 m/s2 = 35.30394 (km/h)/s
Acceleration of Gravity in Imperial Units
1 ag = 1 g = 32.174 ft/s2 = 386.1 in/s2= 22 mph/s
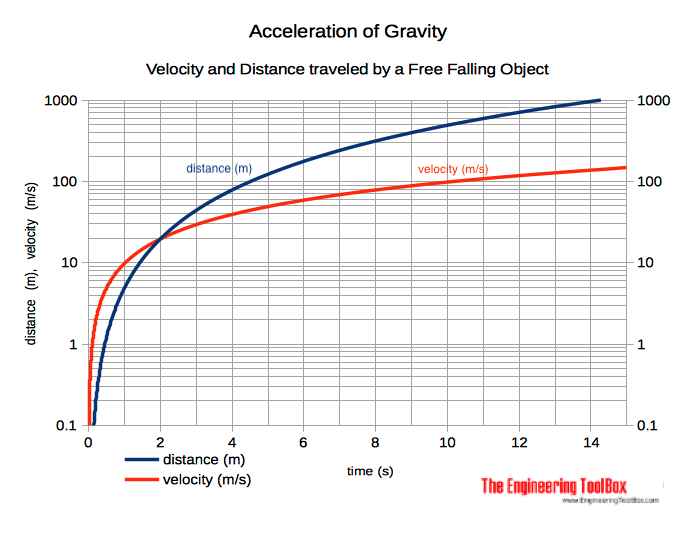
Velocity and Distance Traveled by a Free Falling Object
The velocity for a free falling object after some time can be calculated as:
v = ag t (3)
where
v = velocity (m/s)
The distance traveled by a free falling object after some time can be expressed as:
s = 1/2 ag t2 (4)
where
s = distance traveled by the object (m)
The velocity and distance traveled by a free falling object:
Free Falling Object - Velocity and Distance Traveled vs. Time
| Time (s) | Velocity | Distance | ||||
|---|---|---|---|---|---|---|
| m/s | km/h | ft/s | mph | m | ft | |
| 1 | 9.8 | 35.3 | 32.2 | 21.9 | 4.9 | 16.1 |
| 2 | 19.6 | 70.6 | 64.3 | 43.8 | 19.6 | 64.3 |
| 3 | 29.4 | 106 | 96.5 | 65.8 | 44.1 | 144.8 |
| 4 | 39.2 | 141 | 128.7 | 87.7 | 78.5 | 257.4 |
| 5 | 49.1 | 177 | 160.9 | 110 | 122.6 | 402.2 |
| 6 | 58.9 | 212 | 193.0 | 132 | 176.6 | 579.1 |
| 7 | 68.7 | 247 | 225.2 | 154 | 240.3 | 788.3 |
| 8 | 78.5 | 283 | 257.4 | 176 | 313.9 | 1,029.6 |
| 9 | 88.3 | 318 | 289.6 | 198 | 397.3 | 1,303.0 |
| 10 | 98.1 | 353 | 321.7 | 219 | 490.5 | 1,608.7 |
Note! Velocities and distances are achieved without aerodynamic resistance ( vacuum conditions). The air resistance - or drag force - for objects at higher velocities can be significant - depending on shape and surface area.
Example - Free Falling Stone
A stone is dropped from 1470 ft (448 m) - approximately the height of Empire State Building. The time it takes to reach the ground (without air resistance) can be calculated by rearranging (4) :
t = (2 s / ag )1/2
= (2 (1470 ft) / (32.174 ft/s2))1/2
= 9.6 s
The velocity of the stone when it hits the ground can be calculated with (3) :
v = (32.174 ft/s2) (9.6 s)
= 308 ft/s
= 210 mph
= 94 m/s
= 338 km/h
Example - A Ball Thrown Straight Up
A ball is thrown straight up with an initial velocity of 25 m/s . The time before the ball stops and start falling down can be calculated by modifying (3) to
t = v / ag
= (25 m/s) / (9.81 m/s2)
= 2.55 s
The distance traveled by the ball before it turns and start falling down can be calculated by using (4) as
s = 1/2 (9.81 m/s2) ( 2.55 s)2
= 31.8 m
Newton's First Law
"Every body continues in a state of rest or in a uniform motion in a straight line, until it is compelled by a force to change its state of rest or motion."
Newton's Third Law
"To every action there is always an equal reaction - if a force acts to change the state of motion of a body, the body offers a resistance equal and directly opposite to the force."
Common Expressions
- superimposed loads: kN/m2
- mass loads: kg/m2 or kg/m3
- stress: N/mm2
- bending moment: kNm
- shear: kN
- 1 N/mm = 1 kN/m
- 1 N/mm2 = 103 kN/m2
- 1 kNm = 106 Nmm
Latitude and Acceleration of Gravity
Acceleration of gravity varies with latitude - examples:
Acceleration of Gravity vs. Location and Latitude
| Location | Latitude | Acceleration of Gravity (m/s2) |
|---|---|---|
| North Pole | 90° 0' | 9.8321 |
| Anchorage | 61° 10' | 9.8218 |
| Greenwich | 51° 29' | 9.8119 |
| Paris | 48° 50' | 9.8094 |
| Washington | 38° 53' | 9.8011 |
| Panama | 8° 55' | 9.7822 |
| Equator | 0° 0' | 9.7799 |