Maths - Projections of lines on planes (original) (raw)
This was my original working before Xavier pointed out the inconsistencies. (back to main page)
Alternative using Matrix representation
perpendicular component
A 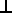 B = (A
B = (A 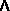 B) * B/|B|2
B) * B/|B|2
A 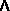 B can be calculated as follows:
B can be calculated as follows:
x = Ay * Bz - By * Az
y = Az * Bx - Bz * Ax
z = Ax * By - Bx * Ay
So,
(A 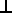 B)x = ((Az * Bx - Bz * Ax) * Bz - By * (Ax * By - Bx * Ay)) / (Bx2 + By2 + Bz2)
B)x = ((Az * Bx - Bz * Ax) * Bz - By * (Ax * By - Bx * Ay)) / (Bx2 + By2 + Bz2)
(A 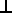 B)y = ((Ax * By - Bx * Ay) * Bx - Bz * (Ay * Bz - By * Az)) / (Bx2 + By2 + Bz2)
B)y = ((Ax * By - Bx * Ay) * Bx - Bz * (Ay * Bz - By * Az)) / (Bx2 + By2 + Bz2)
(A 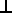 B)z = ((Ay * Bz - By * Az) * By - Bx * (Az * Bx - Bz * Ax)) / (Bx2 + By2 + Bz2)
B)z = ((Ay * Bz - By * Az) * By - Bx * (Az * Bx - Bz * Ax)) / (Bx2 + By2 + Bz2)
grouping terms,
(A 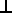 B)x = (Az * Bx* Bz - Bz * Ax* Bz - Ax * By* By + Bx * Ay* By) / (Bx2 + By2 + Bz2)
B)x = (Az * Bx* Bz - Bz * Ax* Bz - Ax * By* By + Bx * Ay* By) / (Bx2 + By2 + Bz2)
(A 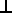 B)y = (Ax * By* Bx - Bx * Ay* Bx - Ay * Bz*Bz + By * Az*Bz) / (Bx2 + By2 + Bz2)
B)y = (Ax * By* Bx - Bx * Ay* Bx - Ay * Bz*Bz + By * Az*Bz) / (Bx2 + By2 + Bz2)
(A 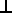 B)z = (Ay * Bz* By - By * Az* By - Az * Bx*Bx + Bz * Ax*Bx) / (Bx2 + By2 + Bz2)
B)z = (Ay * Bz* By - By * Az* By - Az * Bx*Bx + Bz * Ax*Bx) / (Bx2 + By2 + Bz2)
In matrix form,
(A 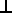 B) = 1 / (Bx2 + By2 + Bz2)* B) = 1 / (Bx2 + By2 + Bz2)* |
-Bz* Bz- By* By Bx * By Bx* Bz By* Bx -Bx*Bx- Bz*Bz By *Bz Bz *Bx Bz* By -By*By- Bx*Bx | [A] |
|---|
I think the signs of all terms should be inverted, see error heading below, can anyone help?
Alternative Form
As pointed out here, If B is normalised (unit length) then Bx2 + By2 + Bz2 =1 so we get:
(A 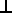 B) = B) = |
Bx*Bx - 1 Bx * By Bx* Bz By* Bx By*By- 1 By *Bz Bz *Bx Bz* By Bz*Bz - 1 | [A] |
|---|
which is:
| (A 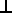 B) = ( | | * | | -[I])[A] |
| ------------------------------------------------------------------------------------------------- | | -- | | ------------- |
B) = ( | | * | | -[I])[A] |
| ------------------------------------------------------------------------------------------------- | | -- | | ------------- |
which is:
(A 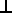 B) = (B * Bt - [I]) [A]
B) = (B * Bt - [I]) [A]
where:
- [I] = unit matrix
- Bt = transpose of B vector
As this is quite a simple equation I wonder if there is a simpler way to derive it? perhaps the method of least squares discussed here.
parallel component
A || P = A • P * P/|B|2
A • P can be calculated as follows:
Ax * Bx + Ay * By + Az * Bz
so,
(A || P)x = (Ax * Bx + Ay * By + Az * Bz) * Bx / (Bx2 + By2 + Bz2)
(A || P)y = (Ax * Bx + Ay * By + Az * Bz) * By/ (Bx2 + By2 + Bz2)
(A || P)z = (Ax * Bx + Ay * By + Az * Bz) * Bz/ (Bx2 + By2+ Bz2)
in matrix form this is:
| (A || P) = 1 / (Bx2 + By2 + Bz2)* | Bx2 Bx * By Bx * Bz By * Bx By2 By * Bz Bz * Bx Bz * By Bz2 | [A] | | ------------------------------------- | ----------------------------------------------------------------- | ----- |
Alternative Form
If B is normalised (unit length) then Bx2 + By2 + Bz2 =1 so we get:
| (A || P) = | Bx * Bx Bx * By Bx * Bz By * Bx By * By By * Bz Bz * Bx Bz * By Bz * Bz | [A] | | ----------- | -------------------------------------------------------------------------------- | ----- |
which is:
| (A 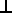 P) = ( | | * | | )[A] |
| ------------------------------------------------------------------------------------------------- | | -- | | ------ |
P) = ( | | * | | )[A] |
| ------------------------------------------------------------------------------------------------- | | -- | | ------ |
which is:
(A 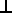 P) = (B * Bt) [A]
P) = (B * Bt) [A]
where:
- Bt = transpose of B vector
As this is quite a simple equation I wonder if there is a simpler way to derive it? perhaps the method of least squares discussed here.
Error
we have shown above that:
A = A || B + A 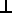 B
B
which would give:
A = (B * Bt - [I] + B * Bt)[A]
which should simplify to A = [I][A] but it does not so it looks like the sign of (A  B) is inverted can anyone see where I went wrong?
B) is inverted can anyone see where I went wrong?
This site may have errors. Don't use for critical systems.
Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.