Maximal gaps between prime k-tuples (original) (raw)
Maximal gaps between prime k-tuples
© 2011-2013 by Alexei Kourbatov, JavaScripter.net/math.
An extended version of this article is now available:
Journal of Integer Sequences: Maximal gaps between prime k-tuples: a statistical approach, Article 13.5.2, MR3065331, arXiv:1301.2242.
Gaps between consecutive primes have been extensively studied [1–8, 20–23]. The prime number theorem [6] suggests that �typical� prime gaps near p have the size about log p. On the other hand, Cramér [7] conjectured that maximal gaps between primes near p are_at most_ about as large as log2_p_ when p → ∞. Moreover, Shanks [8] stated that the maximal gaps are asymptotically equal to log2_p_. All maximal gaps between primes are now known, up to low 19-digit primes [1–5, 23]. This data apparently supports the Cramér and Shanks conjectures: thus far, if we divide by log2_p_ the prime gap ending at p, the resulting ratio is always less than one – but tends to grow closer to one, albeit very slowly and irregularly.
Less is known about maximal gaps between prime constellations, or prime k-tuples [9–14, 19, 24]. We can conjecture that average gaps between prime _k_-tuples near p_are O(log_k p) as p → ∞, in agreement with the Hardy-Littlewood k_-tuple conjecture [9,14]. Computations show that maximal gaps between k_-tuples are at most about log p times the average gap, which implies that maximal gaps are O(log_k+1_p)as p → ∞.Probability-based heuristics described below suggests a general formula predicting the size of maximal gaps between k_-tuples: maximal gaps are approximately max(a, a(log(p/a) − b)), where a = Ck_log_k p is the estimated average gap near p, and Ck and b are positive parameters depending on the type of k_-tuple. This formula approximates maximal gaps better and in a wider range than a linear function of log_k+1_p(cf. Rodriguez and Rivera [12] for the special case k = 2; note the issues caused by a linear approximation). In what follows, we will focus on three specific types of prime _k_-tuples:
- twin primes (k = 2),
- prime quadruplets (k = 4), and
- prime sextuplets (k = 6).
The observations can be generalized to other _k_-tuples; however, the numeric constants will change depending on the specific type of _k_-tuple. See Appendixes for data on maximal gaps between primetriplets (k = 3),quintuplets (k = 5),septuplets (k = 7), anddecuplets (k = 10).
Definitions and notation
Twin primes are pairs of consecutive primes that have the form {p, p+2}. This is the densest repeatable pattern of two primes.
Prime quadruplets are clusters of four consecutive primes of the form {p, p+2, p+6, p+8}. This is the densest repeatable pattern of four primes.
Prime sextuplets are clusters of six consecutive primes of the form {p, p+4, p+6, p+10, p+12, p+16}. This is the densest repeatable pattern of six primes.
Prime k-tuples are clusters of k consecutive primes that have a repeatable pattern. Thus, twin primes are a specific type of prime _k_-tuples, with k = 2;prime quadruplets are another specific type of prime _k_-tuples, with k = 4; and prime sextuplets are yet another type of prime _k_-tuples, with k = 6.(The densest _k_-tuples possible for a given k may also be called prime constellations or prime _k_-tuplets.)
Gaps between prime _k_-tuples are center-to-center distances between consecutive _k_-tuples. If the prime at the �far� end of the gap is p, we denote the gap gk(p). For example, the gap between the quadruplets {11,13,17,19} and {101,103,107,109} is _g_4(101) = 90.The gap between the twin primes {17,19} and {29,31} is _g_2(29) = 12.
A maximal gap is a gap that is strictly greater than all preceding gaps. In other words, a maximal gap is the first occurrence of a gap _at least this size.As an example, consider gaps between prime quadruplets (4-tuples): the gap of 90 preceding the quadruplet {101,103,107,109} is a maximal gap (i.e. the first occurrence of a gap of at least 90), while the gap of 90 preceding {191,193,197,199} is not a maximal gap (not the first occurrence of a gap at least this size). A synonym for maximal gap is record gap; see e.g. OEIS Sequences A113274,A113404,A200503(record gaps between twins, quadruplets, and sextuplets, respectively).
Hereafter p denotes a prime, log x denotes the natural logarithm of x, and log_k x = (log x)k is log x raised to the _k_-th power.
Simple conjectures for the gap size
There are simple formulas for gaps between k_-tuples of a specific type. These formulas give rough estimates of the gap gk(p) that ends at a prime p:
(A) Average gaps between prime k-tuples are gk(p) ≈ Ck log_k p ≡ a(p), where Ck are constants.
(B) Maximal gaps between prime k-tuples are O(log_k_+1_p_): gk(p) < Mk log_k_+1_p_, where Mk ≈ Ck.
(C) Maximal gaps between prime k-tuples are asymptotically equal to Ck_log_k+1_p_ as p → ∞.
Statement (A) follows from the Hardy-Littlewood _k_-tuple conjecture [9,14] that predicts the total counts of prime _k_-tuples (and thereby average frequencies of _k_-tuples); the constants Ck are reciprocals of theHardy-Littlewood constants. For example,
_C_2 ≈ 0.75739... (for twin primes)
_C_3 ≈ 0.34986... (for prime triplets)
C_4 ≈ 0.240895... (for prime quadruplets)
C_6 ≈ 0.057808... (for prime sextuplets).
Statements (B) and (C) are also conjectural – they are suggested by heuristics and supported by large sets of known maximal gaps such as listed below for k = 2, 4, 6.(For more data, see Appendixes as well as the following OEIS sequences: maximal gaps between triplets A201596, A201598, quintuplets A201062, A201073, septuplets A201051, A201251, and decuplets A202281 and A202361. Data in these sequences thus far seem to support our general conjectures –or at least do not contradict them. However, one would need to analyze huge amounts of additional data, especially for k_-tuples with larger k, to boost the confidence level. Of course, no amount of data can replace a formal proof – which we do not have at this time, much like we still lack a formal proof of similar conjectures for primes [7,8].)
The constants Mk (k ≥ 2) in (B) are less than 1; moreover, computations suggest that Mk ≈ Ck.In particular, for k = 2, 4, 6 statement (B) becomes:
Maximal gaps between 2-tuples (twin prime pairs) are O(log3_p): g_2(p) < 0.76 log3_p.
Maximal gaps between 4-tuples (prime quadruplets) are O(log5_p): g_4(p) < 0.241 log5_p.
Maximal gaps between 6-tuples (prime sextuplets) are O(log7_p): g_6(p) < 0.058 log7_p.
Statement (C) is stronger than (B) and analogous to the Shanks conjecture for primes [8]. Together, statements (A), (B), (C) tell us that:
Maximal gaps between prime k-tuples are at most about log p times the average gap.
Can we predict the maximal gaps even better?
Probability-based heuristics can help!
Prime _k_-tuples are rare and seemingly random. Life offers many examples of unusually large intervals between rare random events: the longest runs of two-dice rolls without getting a twelve, maximal intervals between cars crossing a bridge at night, maximal intervals between clicks of a Geiger counter measuring very low radioactivity, etc. Schilling gives many more statistical examples of this kind in his paper The longest run of heads [15] and states �the log n law� for the length or duration of the longest runs. Reasoning as in [15], one can statistically estimate the expected maximal intervals between rare random eventsby expressing the maximal intervals in terms of the average intervals:
E(max interval) = a log(T/a) + O(a), with standard deviation of about a,
where a is the average interval between the rare events, and T is the total observation time or length(1 << a << T).
For lack of a better model, we will simulate the distribution of prime _k_-tuples by a timeline of rare random events. (A quick nod to purists: Yes, we have to remember that consecutive prime k_-tuples are not independent events; thus they are beyond the proven range of applicability of most statistical models. The same is true for consecutive primes. But we are not proving a theorem here – just stating conjectures.)By analogy with the above statistical formula, for maximal gaps gk(p)we define a heuristic maximal gap estimator E(max gk(p)) –a function of p, with two more positive arguments, a and b:
E(max gk(p)) = max(a, a log(p/a) − ba), with a = Ck log_k p.
Here, the role of the total observation time T is played by p(we are looking for maximal gaps that occur from 0 up to p). The role of average intervals a is played by the size of average gaps between k_-tuples near p, i.e. we set a = Ck log_k p,as predicted by the Hardy-Littlewood _k_-tuple conjecture – see (A) above. The constants Ck are reciprocal to the Hardy-Littlewood constants, which are known to a high precision [9,11]. For instance, in case of twin primes (k = 2) we have a value reciprocal to the twin prime constant 2Π2:_C_2 = (2Π2)−1 = (1.3203236...)−1 = 0.75739...Unlike simpler statistical problems with constant a, in our case the average gap a itself grows with p. (Using the Geiger counter analogy, this means that during a very long observation time _T_the radioactivity level not only is low, but gradually gets even lower, so the average intervals between clicks grow longer and longer.) The additional parameter b helps us compensate for this growth and achieve a better fit with known data on _k_-tuples. The choice b ≈ 2/k works well in most cases; the choice b ≈ 3 works even better for k = 1(i.e. for maximal gaps between primes).
Is the prediction accurate?
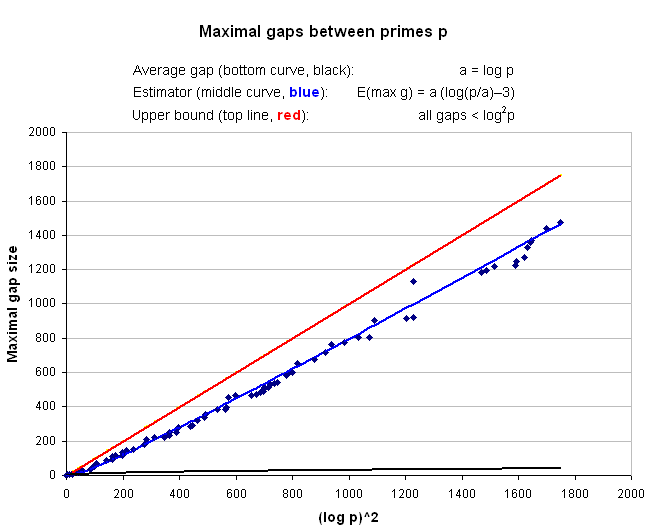
Below are graphs and numerical data for k = 2, 4, 6.The diamond-shaped data points on the graphs are the actual maximal gaps between k_-tuples obtained from a lengthy computation. We easily see that all maximal gaps gk(p)are smaller than the empirical upper bound Ck_log_k+1_p (top red line). The estimator (blue curve) E(max gk) = a(log(p/a) − b)approximates the actual maximal gaps quite closely (usually predicting the maximal gap sizes with accuracy ±2_a_ or better). At first, the estimator curve seems to go way below the respective upper bound (red line). However, substituting a = Ck log_k_ p we can rewrite the estimator as
E(max gk) = a log(p/a) − ab = a log p − a(log a + b) = Ck_log_k+1_p_ − o(log_k_+1_p_),
which shows that E(max gk) < Ck_log_k+1_p_, but at the same time_E_(max gk) is asymptotically equal to the upper bound Ck_log_k+1_p_ as p → ∞. This means that eventually the red line and blue curve will become �almost parallel� as p → ∞. That is to say, if the slope of the red line were even a little less than Ck – while the blue curve were to remain as it is – then the red line would intersect the blue curve at some (very distant) point.
**Notes.**Of course, it is not guaranteed that the formula a(log(p/a) − b) is valid for very big p. Importantly, for any p, the estimator does not predict the existence of a maximal gap gk(p) anywhere near p – it only gives us a good guess for the size of gk(p) if there is a maximal gap near p. As far as rigorous proofs are concerned, we don't even know whether there are infinitely many k-tuples of a given type − for example, whether there are infinitely many twin primes for k = 2. (The famous twin prime conjectureas well as the more general _k_-tuple conjecturethus far remain unproven. Thanks to the theorems of Zhang [21] and Maynard [22], we now know that at least some types of prime _k_-tuples do occur infinitely often.)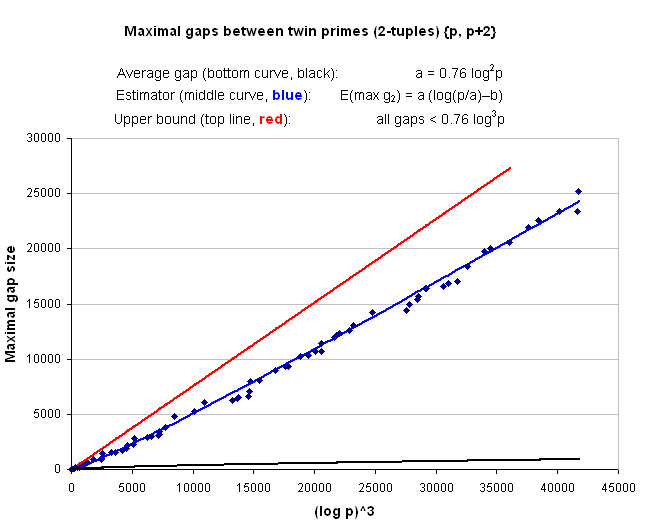
Maximal gaps between twin primes up to 1.2 × 1015
1st twin pair: 2nd twin pair: Gap g2(p):
3 5 2
5 11 6
17 29 12
41 59 18
71 101 30
311 347 36
347 419 72
659 809 150
2381 2549 168
5879 6089 210
13397 13679 282
18539 18911 372
24419 24917 498
62297 62927 630
187907 188831 924
687521 688451 930
688451 689459 1008
850349 851801 1452
2868959 2870471 1512
4869911 4871441 1530
9923987 9925709 1722
14656517 14658419 1902
17382479 17384669 2190
30752231 30754487 2256
32822369 32825201 2832
96894041 96896909 2868
136283429 136286441 3012
234966929 234970031 3102
248641037 248644217 3180
255949949 255953429 3480
390817727 390821531 3804
698542487 698547257 4770
2466641069 2466646361 5292
4289385521 4289391551 6030
19181736269 19181742551 6282
24215097497 24215103971 6474
24857578817 24857585369 6552
40253418059 40253424707 6648
42441715487 42441722537 7050
43725662621 43725670601 7980
65095731749 65095739789 8040
134037421667 134037430661 8994
198311685749 198311695061 9312
223093059731 223093069049 9318
353503437239 353503447439 10200
484797803249 484797813587 10338
638432376191 638432386859 10668
784468515221 784468525931 10710
794623899269 794623910657 11388
1246446371789 1246446383771 11982
1344856591289 1344856603427 12138
1496875686461 1496875698749 12288
2156652267611 2156652280241 12630
2435613754109 2435613767159 13050
4491437003327 4491437017589 14262
13104143169251 13104143183687 14436
14437327538267 14437327553219 14952
18306891187511 18306891202907 15396
18853633225211 18853633240931 15720
23275487664899 23275487681261 16362
23634280586867 23634280603289 16422
38533601831027 38533601847617 16590
43697538391391 43697538408287 16896
56484333976919 56484333994001 17082
74668675816277 74668675834661 18384
116741875898981 116741875918727 19746
136391104728629 136391104748621 19992
221346439666109 221346439686641 20532
353971046703347 353971046725277 21930
450811253543219 450811253565767 22548
742914612256169 742914612279527 23358
1121784847637957 1121784847661339 23382
1149418981410179 1149418981435409 25230
The ratio g_2(p)/log3_p is never greater than 0.76. (The maximal values of _g_2(p) for p up to 1.2 × 1015 were first computed in 2008 by Richard Fischer [13] and later extended by Tomás Oliveira e Silva [24].)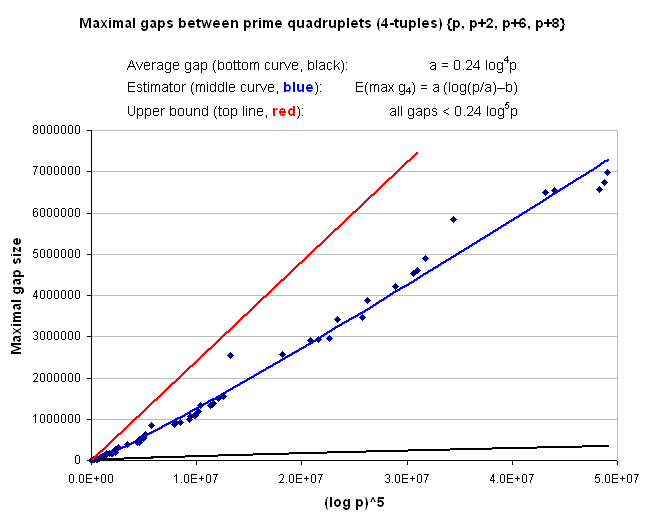
Maximal gaps between prime quadruplets up to 1015:
1st 4-tuple: 2nd 4-tuple: Gap g4(p):
5 11 6
11 101 90
191 821 630
821 1481 660
2081 3251 1170
3461 5651 2190
5651 9431 3780
25301 31721 6420
34841 43781 8940
88811 97841 9030
122201 135461 13260
171161 187631 16470
301991 326141 24150
739391 768191 28800
1410971 1440581 29610
1468631 1508621 39990
2990831 3047411 56580
3741161 3798071 56910
5074871 5146481 71610
5527001 5610461 83460
8926451 9020981 94530
17186591 17301041 114450
21872441 22030271 157830
47615831 47774891 159060
66714671 66885851 171180
76384661 76562021 177360
87607361 87797861 190500
122033201 122231111 197910
132574061 132842111 268050
204335771 204651611 315840
628246181 628641701 395520
1749443741 1749878981 435240
2115383651 2115824561 440910
2128346411 2128859981 513570
2625166541 2625702551 536010
2932936421 2933475731 539310
3043111031 3043668371 557340
3593321651 3593956781 635130
5675642501 5676488561 846060
25346635661 25347516191 880530
27329170151 27330084401 914250
35643379901 35644302761 922860
56390149631 56391153821 1004190
60368686121 60369756611 1070490
71335575131 71336662541 1087410
76427973101 76429066451 1093350
87995596391 87996794651 1198260
96616771961 96618108401 1336440
151023350501 151024686971 1336470
164550390671 164551739111 1348440
171577885181 171579255431 1370250
210999769991 211001269931 1499940
260522319641 260523870281 1550640
342611795411 342614346161 2550750 1970587668521 1970590230311 2561790
4231588103921 4231591019861 2915940
5314235268731 5314238192771 2924040
7002440794001 7002443749661 2955660
8547351574961 8547354997451 3422490
15114108020021 15114111476741 3456720
16837633318811 16837637203481 3884670
30709975578251 30709979806601 4228350
43785651890171 43785656428091 4537920
47998980412211 47998985015621 4603410
55341128536691 55341133421591 4884900
92944027480721 92944033332041 5851320
412724560672211 412724567171921 6499710
473020890377921 473020896922661 6544740
885441677887301 885441684455891 6568590
947465687782631 947465694532961 6750330
979876637827721 979876644811451 6983730
The ratio g_4(p)/log5_p is never greater than 0.241.
Maximal gaps between prime 6-tuples up to 1015:
1st 6-tuple: 2nd 6-tuple: Gap g6(p):
7 97 90
97 16057 15960
19417 43777 24360
43777 1091257 1047480
3400207 6005887 2605680
11664547 14520547 2856000
37055647 40660717 3605070
82984537 87423097 4438560
89483827 94752727 5268900
94752727 112710877 17958150
381674467 403629757 21955290
1569747997 1593658597 23910600
2019957337 2057241997 37284660
5892947647 5933145847 40198200
6797589427 6860027887 62438460
14048370097 14112464617 64094520
23438578897 23504713147 66134250
24649559647 24720149677 70590030
29637700987 29715350377 77649390
29869155847 29952516817 83360970
45555183127 45645253597 90070470
52993564567 53086708387 93143820
58430706067 58528934197 98228130
93378527647 93495691687 117164040
97236244657 97367556817 131312160
240065351077 240216429907 151078830
413974098817 414129003637 154904820
419322931117 419481585697 158654580
422088931207 422248594837 159663630
427190088877 427372467157 182378280
610418426197 610613084437 194658240
659829553837 660044815597 215261760
660863670277 661094353807 230683530
853633486957 853878823867 245336910 1089611097007 1089869218717 258121710
1247852774797 1248116512537 263737740
1475007144967 1475318162947 311017980
1914335271127 1914657823357 322552230
1953892356667 1954234803877 342447210
3428196061177 3428617938787 421877610
9367921374937 9368397372277 475997340
10254799647007 10255307592697 507945690
13786576306957 13787085608827 509301870
21016714812547 21017344353277 629540730
33157788914347 33158448531067 659616720
41348577354307 41349374379487 797025180
72702520226377 72703333384387 813158010
89165783669857 89166606828697 823158840
122421000846367 122421855415957 854569590
139864197232927 139865086163977 888931050
147693859139077 147694869231727 1010092650
186009633998047 186010652137897 1018139850
202607131405027 202608270995227 1139590200
332396845335547 332397997564807 1152229260
424681656944257 424682861904937 1204960680
437804272277497 437805730243237 1457965740
The ratio g_6(p)/log7_p is never greater than 0.058; in fact, for all of the above gaps _g_6(p), the ratio is far less.
On maximal gaps between primes
For comparison, here is the same model applied to maximal gaps between primes (A005250):
Maximal gaps are about a(log(p/a) − b),with a = log p and b ≈ 3.
This leads to the well-known Cramér and Shanks conjectures for prime gaps g(p):
lim sup(g(p)/log2_p_) = 1 as p → ∞ (Cramér [7]),
while maximal gaps between consecutive primes are asymptotically equal to log2_p_ (Shanks [8]).
Indeed, for a = log p and any fixed b ≥ 0, we have log2_p_ > a(log(p/a) − b)~log2_p_as p → ∞.
An adjustment to the Cramér-Shanks conjecture? Maier's theorem [16] states that there are (relatively short) intervals where typical gaps between primes are greater than the average (log p). Based in part on this theorem, Granville [17] adjusted the Cramér-Shanks conjecture and proposed that, as p → ∞, lim sup(g(p)/log2_p_) ≥ 2_e_−γ = 1.1229...This would mean that an infinite subsequence of maximal gaps must lie above_the Cramér-Shanks upper limit log2_p, i.e. above the red line on this graph – and this hypothetical subsequence (or an infinite subset thereof) must approach a line whose slope is about 1.1229 times steeper! However, for now, there is not a single data point for maximal prime gaps above log2_p_, where p denotes the end-of-gap prime. Apparently Helmut Maier himself did not feel that the Cramér-Shanks conjecture was necessarily in danger because of his theorem; thus, Maier and Pomerance [18] simply remarked in 1990 (five years after the publication of Maier's theorem):
Cramér conjectured that lim sup G(x) / log2_x_ = 1, while Shanks made the stronger conjecture that G(x)~log2_x_, but we are still a long way from proving these statements.
[Here G(x) denotes the largest prime gap below x.]
So do we possibly need a constant before log2_x_ in the asymptotic equivalence G(x)~log2_x_? Or maybe the asymptotic equivalence is not valid at all? Maybe the best way we can hope to describe the maximal prime gaps is in weaker terms of an upper limit, lim sup (G(x)/log2_x_)?We'll live and see! (Let us hope to live long enough...)
Appendixes
The above heuristic argument appears to be applicable to prime _k_-tuples for all natural k, as long as the Hardy-Littlewood _k_-tuple conjecture [9,14] remains valid. However, we have purposely chosen only the cases k = 2, 4, 6 for the main presentation above. Data and specific conjectures for other values of k can be found in these appendixes:
- Maximal gaps between prime triplets (k = 3)
- Maximal gaps between prime quintuplets (k = 5)
- Maximal gaps between prime septuplets (k = 7)
- Maximal gaps between prime decuplets (k = 10)
- Hardy-Littlewood constants and reciprocals
References
1. Young, J. and Potler, A. First Occurrence Prime Gaps. Math. Comp. 52, 221-224, 1989.
2. Nicely, Thomas R. List of prime gaps. http://www.trnicely.net/gaps/gaplist.html (2011)
3. Oliveira e Silva, Tomás. Gaps between consecutive primes. http://www.ieeta.pt/\~tos/gaps.html (2001-2013)
4. Ribenboim, Paulo. The little book of big primes, New York, Springer-Verlag, 1991.
(Second edition: The little book of bigger primes, New York, Springer-Verlag, 2004)
5. Weisstein, Eric W. Prime Gaps. From MathWorld – A Wolfram Web Resource.
http://mathworld.wolfram.com/PrimeGaps.html (2011)
6. Hardy, Godfrey H. and Wright, Edward M. An Introduction to the Theory of Numbers, 6th ed. Oxford, Oxford University Press, 2008, p.10.
7. Cramér, Harald. On the Order of Magnitude of the Difference between Consecutive Prime Numbers. Acta Arith. 2, 23-46, 1936.
8. Shanks, Daniel. On Maximal Gaps Between Successive Primes. Math. Comp. 18, 646-651, 1964.
9. Hardy, Godfrey H. and Littlewood, John E. Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes. Acta Math. 44, 1-70, 1923.
http://www.springerlink.com/index/D700T434065K0230.pdf
10. Smith, Herschel F. On a generalization of the prime pair problem, Mathematical Tables and Other Aids to Computation, v. 11, 1957, p. 274.
http://www.ams.org/journals/mcom/1957-11-060/S0025-5718-1957-0094314-8/home.html
11. Forbes, Anthony D. Prime _k_-tuplets. http://anthony.d.forbes.googlepages.com/ktuplets.htm (2011)
12. Rivera, Carlos and Rodriguez, Luis. Gaps between consecutive twin prime pairs
http://www.primepuzzles.net/conjectures/conj\_066.htm
13. Fischer, Richard. Maximale Lücken (Intervallen) von Primzahlenzwillingen.
http://www.fermatquotient.com/PrimLuecken/ZwillingsRekordLuecken (2008)
14. Weisstein, Eric W. k-Tuple Conjecture. From MathWorld – A Wolfram Web Resource.
http://mathworld.wolfram.com/k-TupleConjecture.html (2011)
15. Schilling, Mark F. The longest run of heads. The College Mathematics Journal, v.21, No.3, 196-207, 1990.
16. Maier, Helmut. Primes in short intervals, Michigan Math. J., v.32, 221-225, 1985.
17. Granville, Andrew. Harald Cramér and the distribution of prime numbers. Scand. Act. J. 1, 12-28, 1995.
http://www.dms.umontreal.ca/\~andrew/PDF/cramer.pdf
18. Maier, Helmut and Pomerance, Carl. Unusually large gaps between consecutive primes. Transactions of the AMS, v.322, No. 1, 201-237, 1990.
19. Wolf, Marek. Some remarks on the distribution of twin primes, http://arxiv.org/abs/math/0105211 (2001)
20. Wolf, Marek. Some heuristics on the gaps between consecutive primes, http://arxiv.org/abs/1102.0481 (2011)
2013 — New Proofs
21. Zhang, Yitang. Bounded gaps between primes, Annals of Math. 179, No.3, 1121-1174, 2014.
22. Maynard, James. Small gaps between primes, http://arxiv.org/abs/1311.4600 (2013)
Recent Computations and Heuristics
23. Oliveira e Silva, Tomás, Herzog, Siegfried, and Pardi, Silvio. Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4�1018, Math. Comp. 83, 2033-2060, 2014.
24. Oliveira e Silva, Tomás, Gaps between twin primes. http://sweet.ua.pt/tos/twin\_gaps.html (2013)
25. Kourbatov, Alexei, Maximal gaps between prime k-tuples: a statistical approach. Journal of Integer Sequences, 16, Article 13.5.2, 2013. arXiv:1301.2242
26. Kourbatov, Alexei, Tables of record gaps between prime constellations, arXiv:1309.4053 (2013)
27. Kourbatov, Alexei, The distribution of maximal prime gaps in Cramer's probabilistic model of primes, Int. Journal of Statistics and Probability, 3, No.2, 18-29, 2014. arXiv:1401.6959
Copyright© 2011-2014, Alexei Kourbatov, JavaScripter.net.